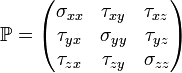Contenido Checked

Mecánica de Fluidos

Temas relacionados: Matemáticas

Acerca de este escuelas selección Wikipedia

SOS Children hizo esta selección Wikipedia junto a otros recursos de escuelas . Apadrinar un niño para hacer una diferencia real.

Mecánica de medios continuos
BernoullisLawDerivationDiagram.svg

Mecánica de fluidos es el estudio de cómo fluidos se mueven y las fuerzas en ellos. (Los líquidos incluyen los líquidos y los gases .) Mecánica de fluidos se pueden dividir en estática de fluidos, el estudio de los fluidos en reposo, y dinámica de fluidos, el estudio de los fluidos en movimiento. Es una rama de mecánica de medios continuos, un tema que los modelos son importantes sin necesidad de utilizar la información que está hecho de átomos. El estudio de la mecánica de fluidos se remonta al menos a la época de la antigua Grecia, cuando Arquímedes hizo un comienzo en la estática de fluidos. Sin embargo, la mecánica de fluidos, especialmente la dinámica de fluidos, es un campo activo de investigación con muchos problemas sin resolver o parcialmente resueltas. Mecánica de fluidos pueden ser matemáticamente compleja. A veces es mejor puede ser resuelto por métodos numéricos, por lo general el uso de computadoras. Una disciplina moderna, llamada Dinámica de Fluidos Computacional (CFD), se dedica a este enfoque para resolver problemas de mecánica de fluidos. También aprovechando la naturaleza altamente visual del flujo de fluido se Velocimetría de imágenes de partículas, un método experimental para la visualización y el análisis de flujo de fluido.

Relación con la mecánica de medios continuos

Mecánica de fluidos es una subdisciplina de la mecánica de medios continuos, como se ilustra en la siguiente tabla.

Mecánica del continuo estudio de la física de materiales continuos Mecánica de sólidos: el estudio de la física de materiales continuos con una forma de descanso definido. Elasticidad: que describe los materiales que retornan a su forma de descanso después de una aplicada estrés.
Plasticidad: que describe los materiales que se deforman permanentemente después de un gran esfuerzo aplicado suficiente. Reología: el estudio de materiales con características tanto de sólidos y fluidos
Mecánica de fluidos: el estudio de la física de materiales continuos que adoptan la forma de su recipiente. Fluidos no newtonianos
Fluidos newtonianos

En una vista mecánico, un fluido es una sustancia que no es compatible tensión tangencial; es por eso que un fluido en reposo tiene la forma de su que contiene fluido vessel.And en resto tiene el estrés de cizallamiento cero

Supuestos

Como cualquier modelo matemático del mundo real, la mecánica de fluidos hace que algunos supuestos básicos sobre los materiales que están siendo estudiados. Estos supuestos se convierten en ecuaciones que deben cumplirse para que los supuestos son para ser verdad. Por ejemplo, considere un fluido incompresible en tres dimensiones. La suposición de que se conserva la masa significa que para cualquier superficie cerrada fijo (tal como una esfera) la velocidad de paso de masa desde el exterior hacia el interior de la superficie debe ser la misma que la tasa de masa que pasa a la otra manera. (Alternativamente, la masa permanece constante en el interior, al igual que la masa exterior). Esto puede convertirse en una ecuación integral sobre la superficie.

Mecánica de fluidos asume que cada fluido obedece a lo siguiente:

Además, a menudo es útil (y realista) para asumir un fluido es incompresible - es decir, la densidad del fluido no cambia. Los líquidos a menudo puede ser modelado como fluidos incompresibles, mientras los gases no pueden.

Del mismo modo, a veces puede suponerse que la viscosidad del fluido es cero (el líquido es viscoso). Gases a menudo pueden ser asumidas para ser viscoso. Si un fluido es viscoso, y su flujo contenida de alguna manera (por ejemplo, en una tubería), entonces el flujo en el límite debe tener velocidad cero. Para un fluido viscoso, si el límite no es poroso, las fuerzas de cizallamiento entre el fluido y los resultados de contorno también en la velocidad cero para el fluido en el límite. Esto se llama el condición no deslizante. Para un medio poroso de otra manera, en la frontera del recipiente que contiene, la condición de deslizamiento no es velocidad cero, y el fluido tiene un campo de velocidad discontinua entre el fluido libre y el fluido en el medio poroso (esto está relacionado con la Beavers y Joseph condición).

La hipótesis del continuo

Los líquidos se componen de moléculas que chocan unos con otros y objetos sólidos. El supuesto continuo, sin embargo, considera que los líquidos sean continua. Es decir, las propiedades tales como la densidad, la presión, la temperatura y la velocidad se toman para ser bien definido en "infinitamente" puntos pequeños, la definición de un REV (Referencia de elemento de volumen), en el orden geométrico de la distancia entre dos moléculas adyacentes de fluido. Las propiedades se supone que variar continuamente desde un punto a otro, y se promedian los valores en el REV. El hecho de que el fluido se compone de moléculas discretas se ignora.

La hipótesis del continuo es básicamente una aproximación, en la misma manera que los planetas son aproximados por partículas puntuales cuando se trata de la mecánica celeste, y por lo tanto da lugar a soluciones aproximadas. En consecuencia, la asunción de la hipótesis del continuo puede llevar a resultados que no son de precisión deseada. Dicho esto, en las circunstancias adecuadas, la hipótesis del continuo produce resultados muy precisos.

Esos problemas para los que la hipótesis del continuo no permite soluciones de precisión deseada se resuelven usando la mecánica estadística . Para determinar si se utiliza o no la dinámica de fluidos convencionales o mecánica estadística, la Número de Knudsen se evalúa para el problema. El número de Knudsen se define como la relación de la molecular longitud media de camino libre a una cierta longitud física representante escala. Esta escala de longitud podría ser, por ejemplo, el radio de un cuerpo en un fluido. (Más simplemente, el número de Knudsen es cuántas veces su diámetro una partícula viajará en promedio antes de golpear otra partícula). Problemas con números Knudsen iguales o superiores a la unidad son mejor evaluadas utilizando la mecánica estadística para soluciones fiables.

Ecuaciones de Navier-Stokes

Artículo principal: las ecuaciones de Navier-Stokes

Las ecuaciones de Navier-Stokes (nombrados después Claude-Louis Navier y George Gabriel Stokes) son el conjunto de ecuaciones que describen el movimiento de sustancias fluidas tales como líquidos y gases. Estas ecuaciones establecen que los cambios en el impulso ( aceleración ) de partículas de fluido depende sólo del exterior la presión y las fuerzas viscosas internos (similar a la fricción) que actúa sobre el fluido. Por lo tanto, las ecuaciones de Navier-Stokes describen el equilibrio de fuerzas que actúan en cualquier región dada del fluido.

Las ecuaciones de Navier-Stokes son ecuaciones diferenciales que describen el movimiento de un fluido. Tales ecuaciones establecen relaciones entre las tasas de cambiar las variables de interés. Por ejemplo, las ecuaciones de Navier-Stokes para un fluido ideal con viscosidad cero indica que la aceleración (la tasa de cambio de la velocidad) es proporcional a la derivada de la presión interna.

Esto significa que las soluciones de las ecuaciones de Navier-Stokes para un problema físico dado hay que buscar con la ayuda de cálculo . En términos prácticos sólo los casos más simples pueden resolverse exactamente de esta manera. Estos casos implican generalmente, el flujo no turbulento constante (flujo no cambia con el tiempo) en el que la Número de Reynolds es pequeño.

Para situaciones más complejas, como los sistemas climáticos globales como El Niño o ascensor en un ala, soluciones de las ecuaciones de Navier-Stokes en la actualidad sólo pueden ser encontrados con la ayuda de computadoras. Este es un campo de las ciencias por su propia llamada dinámica de fluidos computacional.

Forma general de la ecuación

La forma general de las ecuaciones de Navier-Stokes para la conservación del momento es:

\ Rho \ frac {D \ mathbf {v}} {D t} = \ nabla \ cdot \ mathbb {P} + \ rho \ mathbf {f}

donde

  • \ Rho es la densidad del fluido,
\ Frac {D} {D t} es el derivado sustantivo (también llamada la derivada material)
  • \ Mathbf {v} es el vector de velocidad,
  • \ Mathbf {f} es el vector de fuerza de cuerpo, y
  • \ Mathbb {P} es un tensor que representa las fuerzas de superficie aplicados sobre una partícula de fluido (el comóvil tensor de tensiones).

A menos que el fluido se compone de grados de libertad de giro como vórtices, \ Mathbb {P} es un tensor simétrico. En general, (en tres dimensiones) \ Mathbb {P} tiene la forma:

\ Mathbb {P} = \ begin {pmatrix} \ sigma_ {xx} & \ tau_ {xy} & \ tau_ {xz} \\ \ tau_ {yx} & \ sigma_ {yy} & \ tau_ {yz} \\ \ tau_ {zx} & \ tau_ {zy} & \ sigma_ {zz} \ end {pmatrix}

donde

  • \ Sigma son tensiones normales, y
  • \ Tau son esfuerzos tangenciales (tensiones de cizallamiento).

Lo anterior es en realidad un conjunto de tres ecuaciones, uno por cada dimensión. Por sí mismos, estos no son suficientes para producir una solución. Sin embargo, la adición de conservación de la masa y de las condiciones de contorno apropiadas para el sistema de ecuaciones produce un conjunto de ecuaciones resoluble.

Fluidos newtonianos vs. no newtonianos

Un fluido newtoniano (el nombre de Isaac Newton ) se define como un fluido cuya tensión de cizallamiento es linealmente proporcional a la velocidad gradiente en la dirección perpendicular al plano de cizalla. Esta definición significa independientemente de las fuerzas que actúan sobre un fluido, que continúa fluyendo. Por ejemplo, el agua es un fluido newtoniano, porque sigue mostrando las propiedades del fluido no importa cuánto se agita o mezcla. Una definición rigurosa es ligeramente menos que el arrastre de un objeto pequeño que se mueve a través del fluido es proporcional a la fuerza aplicada al objeto. (Comparar fricción).

Por el contrario, revolviendo una fluido no newtoniano puede dejar un "agujero" detrás. Esto llenará gradualmente con el tiempo - este comportamiento se observa en materiales tales como pudín, Oobleck, o arena (arena aunque no es estrictamente un fluido). alternativamente, agitar un fluido no newtoniano puede causar la viscosidad para disminuir, de modo que el fluido que aparezca "diluyente" (esto se ve en antigoteo pinturas). Hay muchos tipos de fluidos no newtonianos, tal como se definen a ser algo que no obedece una propiedad particular.

Ecuaciones para un fluido newtoniano

La constante de proporcionalidad entre la tensión de cizallamiento y el gradiente de velocidad se conoce como el viscosidad. Una ecuación simple para describir el comportamiento fluido newtoniano es

\ Tau = - \ mu \ frac {dv} {dx}

donde

\ Tau es la tensión de cizallamiento ejercida por el fluido (" arrastre ")
\ mu es la viscosidad del fluido - una constante de proporcionalidad
\ Frac {dv} {dx} es el gradiente de velocidad perpendicular a la dirección de la cizalladura

Para un fluido newtoniano, la viscosidad, por definición, sólo depende de la temperatura y presión, no en las fuerzas que actúan sobre ella. Si el líquido es incompresible y la viscosidad es constante a través del fluido, la ecuación que gobierna la tensión de cizallamiento (en coordenadas cartesianas ) es

\ Tau_ {ij} = \ mu \ left (\ frac {\ v_i parcial} {\ x_j parcial} + \ frac {\ v_j parcial} {\ x_i parcial} \ right)

donde

\ Tau_ {ij} es la tensión de cizallamiento en la i ^ {ésimo} la cara de un elemento de fluido en el j ^ {º} dirección
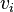v_i es la velocidad en el i ^ {ésimo} dirección
x_j es el j ^ {º} dirección de coordenadas

Si un fluido no obedece esta relación, se denomina una fluido no newtoniano, de los cuales hay varios tipos.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Fluid_mechanics&oldid=194503975 "