
Histograma
Sabías ...
SOS Children, que corre cerca de 200 sos escuelas en el mundo en desarrollo, organizó esta selección. Para comparar obras de caridad de patrocinio este es el mejor vínculo de patrocinio .

En las estadísticas , un histograma es una visualización gráfica de tabulados frecuencias. Un histograma es la versión gráfica de una tabla que muestra qué proporción de casos se encuentra en cada uno de varios o muchos especificado categorías. El histograma se diferencia de una gráfico de barras en la que es la zona de la barra que indica el valor, no la altura, una distinción crucial cuando las categorías no son de anchura uniforme (Lancaster, 1974). Las categorías se suelen especificar como no se solapan intervalos de alguna variable. Las categorías (barras) deben ser adyacentes.
La palabra histograma se deriva del griego : histos 'nada estar en pie "(como los mástiles de un barco, el bar de un telar, o las barras verticales de un histograma);' dibujo, grabar, escribir 'gramma. El histograma es una de las siete herramientas básicas de control de calidad, que también incluyen la Diagrama de Pareto, verifique en la hoja, gráfico de control, diagrama de causa y efecto, diagrama de flujo, y diagrama de dispersión. Una generalización del histograma es kernel técnicas de suavizado. Esto construir una muy suave la función de densidad de probabilidad de los datos suministrados.
Ejemplos
Como ejemplo tenemos en cuenta los datos recogidos por la Oficina del Censo de Estados Unidos a tiempo para ir al trabajo (censo de 2000, , Tabla 5). El censo reveló que había 124 millones de personas que trabajan fuera de sus hogares. Se pide a las personas el tiempo que les toma llegar al trabajo, y sus respuestas se dividieron en categorías: menos de 5 minutos, más de 5 minutos y menos de 10, más de 10 minutos y menos de 15, y así sucesivamente. Las tablas muestran el número de personas por categoría en miles, por lo que 4180 significa 4.180.000.
Los datos en las siguientes tablas se muestran gráficamente por histogramas. Una característica interesante de los dos diagramas es el aumento en la categoría de 30 minutos. Parece probable que esta es una artefacto: media hora es una unidad común de medición del tiempo informal, por lo que las personas cuyos tiempos de viaje eran quizás un poco menos o un poco más de 30 minutos podrían sentirse inclinados a responder "30 minutos". Este redondeo es un fenómeno común en la recogida de datos de las personas.

| Intervalo | Ancho | Cantidad | Cantidad / ancho |
|---|---|---|---|
| 0 | 5 | 4180 | 836 |
| 5 | 5 | 13687 | 2737 |
| 10 | 5 | 18618 | 3723 |
| 15 | 5 | 19634 | 3926 |
| 20 | 5 | 17981 | 3596 |
| 25 | 5 | 7190 | 1438 |
| 30 | 5 | 16369 | 3273 |
| 35 | 5 | 3212 | 642 |
| 40 | 5 | 4122 | 824 |
| 45 | 15 | 9200 | 613 |
| 60 | 30 | 6461 | 215 |
| 90 | 60 | 3435 | 57 |
Este histograma muestra el número de casos por cada intervalo de la unidad para que la altura de cada barra es igual a la proporción de personas en total en la encuesta que caen en esa categoría. El área bajo la curva representa el número total de casos (124 millones). Este tipo de histograma muestra números absolutos.

| Intervalo | Ancho | Cantidad (Q) | Q / Total / anchura |
|---|---|---|---|
| 0 | 5 | 4180 | 0.0067 |
| 5 | 5 | 13687 | 0.0220 |
| 10 | 5 | 18618 | 0.0300 |
| 15 | 5 | 19634 | 0.0316 |
| 20 | 5 | 17981 | 0.0289 |
| 25 | 5 | 7190 | 0.0115 |
| 30 | 5 | 16369 | 0.0263 |
| 35 | 5 | 3212 | 0.0051 |
| 40 | 5 | 4122 | 0.0066 |
| 45 | 15 | 9200 | 0.0049 |
| 60 | 30 | 6461 | 0.0017 |
| 90 | 60 | 3435 | 0.0004 |
Este histograma difiere de la primera sólo en el escala vertical. La altura de cada barra es el porcentaje decimal del total que cada categoría representa, y el área total de todas las barras es igual a 1, el equivalente decimal del 100%. La curva que se muestra es un simple estimación de la densidad. Esta versión muestra proporciones, y también se conoce como un histograma unidad de área.
En otras palabras, un histograma representa una distribución de frecuencias por medio de rectángulos cuyas anchuras representan intervalos de clase y cuyas áreas son proporcionales a las frecuencias correspondientes. Sólo colocan las barras juntos para hacer que sea más fácil para comparar los datos.
Actividades y demostraciones
La Páginas de recursos SOCR contienen una serie de actividades prácticas interactivas que demuestran el concepto de un histograma, un histograma construcción y manipulación usando applets de Java y gráficos.
Definición matemática
En un sentido matemático más general, un histograma es un mapeo  que cuenta el número de observaciones que caen en distintas categorías disjuntos (conocidos como contenedores), mientras que la gráfica de un histograma es simplemente una manera de representar un histograma. Por lo tanto, si dejamos que
que cuenta el número de observaciones que caen en distintas categorías disjuntos (conocidos como contenedores), mientras que la gráfica de un histograma es simplemente una manera de representar un histograma. Por lo tanto, si dejamos que  ser el número total de observaciones y
ser el número total de observaciones y  ser el número total de contenedores, el histograma
ser el número total de contenedores, el histograma  cumple con las siguientes condiciones:
cumple con las siguientes condiciones:

Histograma acumulativo
Un histograma acumulativo es un mapeo que cuenta el número acumulado de observaciones en todos los contenedores hasta la bandeja especificada. Es decir, el histograma acumulativo 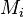 de un histograma
de un histograma  se define como:
se define como:

Número de contenedores y ancho
No hay "mejor" número de contenedores, y diferentes tamaños bin puede revelar diferentes características de los datos. Algunos teóricos han intentado determinar el número óptimo de contenedores, pero estos métodos generalmente hacer fuertes supuestos sobre la forma de la distribución. Siempre se debe experimentar con anchos de caja antes de elegir uno (o más) que ilustran las características más destacadas de los datos.
El número de contenedores  puede calcularse directamente, o desde una anchura bin sugerido
puede calcularse directamente, o desde una anchura bin sugerido  :
:
Las llaves indican la función de techo.
- Fórmula de Sturges

que basa implícitamente los tamaños de basura en el rango de los datos, y puede funcionar mal si  .
.
- Elección de Scott

donde  es el ancho de caja común, y
es el ancho de caja común, y  es la muestra de la desviación estándar .
es la muestra de la desviación estándar .
- Elección Freedman-Diaconis '

que se basa en la rango intercuartil
Datos continuos
La idea de un histograma puede ser generalizado a los datos continuos. Dejar 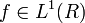 (Ver Lebesgue espacio), entonces el operador histograma acumulativo
(Ver Lebesgue espacio), entonces el operador histograma acumulativo  puede ser definido por:
puede ser definido por:
 con sólo un número finito intervalos de monotonía esto puede reescribirse como
con sólo un número finito intervalos de monotonía esto puede reescribirse como  .
.
 no está definido si
no está definido si  es el valor de una punto estacionario.
es el valor de una punto estacionario.

