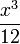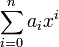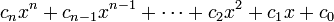Polinomio

En matemáticas , un polinomio es una expresión que se construye a partir de uno o más y las variables constantes, utilizando sólo las operaciones de suma, resta, multiplicación y constantes exponentes de números enteros positivos. Por ejemplo, es un polinomio, pero no es un polinomio, ya que implica la división por una variable y porque tiene un exponente que no es un número entero positivo.

Los polinomios son uno de los conceptos más importantes en álgebra y en toda la matemática y la ciencia. Pueden ser utilizados para formar las ecuaciones polinómicas, que puede codificar una amplia gama de problemas, desde primaria historia de los problemas a los problemas complicados en las ciencias; que pueden ser utilizados para definir funciones polinómicas, que aparecen en la configuración básica que van desde la química y la física a la economía , y se utilizan en el cálculo y análisis numérico a la aproximación de otras funciones. Los polinomios se utilizan en su propio derecho de construir anillos de polinomios, uno de los conceptos más poderosos en el álgebra y geometría algebraica.

Visión de conjunto

Un polinomio es cero, o se puede escribir como la suma de una o más distinto de cero términos. El número de términos es finito. Estos términos se componen de una constante (llamado coeficiente del término) multiplicado por cero o más variables (que por lo general están representados por letras). Cada variable puede tener un exponente que es un número entero no negativo. El exponente en una variable en un plazo es igual a la grado de esa variable en ese término. Desde , El grado de una variable sin un exponente escrito es uno. Un término sin variables se denomina término constante, o simplemente una constante. El grado de un término constante es 0. El coeficiente de un término puede ser cualquier número, incluyendo fracciones, números irracionales, números negativos, y los números complejos.

Por ejemplo,

es un término. La coeficiente es -5, las variables son x e y, el grado de x es de dos, y el grado de Y es uno.

El grado de todo el término es la suma de los grados de cada variable en ella. En el ejemplo anterior, el grado es 2 + 1 = 3.

Un polinomio es una suma de términos. Por ejemplo, el siguiente es un polinomio:

Se compone de tres términos: el primero es el grado dos, el segundo es un grado, y el tercero es de cero grados. Aquí "

"Representa"

", Por lo que el coeficiente del término medio es -5.

Cuando un polinomio en una variable está dispuesta en el orden tradicional, los términos de mayor grado vienen antes de que los términos de grado inferior. En el primer mandato anterior, el coeficiente es 3, la variable es x, y el exponente es 2. En el segundo período, el coeficiente es de -5. El tercer término es una constante. El grado de un polinomio distinto de cero es el mayor grado de cualquier plazo. En el ejemplo, el polinomio tiene grado dos.

Las formas alternativas

Una expresión que se puede convertir en forma polinómica a través de una secuencia de aplicaciones de la conmutativa , asociativa , y leyes distributivas generalmente se considera que es un polinomio. Por ejemplo

es un polinomio, ya que puede ser trabajado a . Del mismo modo

se considera un término válido en un polinomio, a pesar de que se trata de una división, debido a que es equivalente a y es simplemente una constante. Por tanto, el coeficiente de este término es . Por razones similares, si se permite que los coeficientes complejos, uno que muchos tienen un solo término como 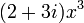; a pesar de que parece que debería ser resuelto a dos términos, el número complejo 2 + 3 i es, de hecho, sólo un coeficiente único en este caso que sucede a exigir un "+" que se escribieran una por una.

La división por una expresión que contiene una variable no se permite generalmente en polinomios. Por ejemplo,

no es un polinomio, ya que incluye la división por una variable. Del mismo modo,

no es un polinomio, porque tiene un exponente variable.

Desde la resta puede ser tratada como adición del aditivo contrario, y desde exponenciación a una fuente de número entero positivo constante puede ser tratada como una multiplicación repetida, polinomios se pueden construir a partir de las constantes y variables con sólo la adición de dos operaciones y la multiplicación.

Funciones polinómicas

Una función polinómica es una función definida por evaluar un polinomio. Por ejemplo, la función f, teniendo números reales a los números reales, definido por

es una función polinómica de una variable. Funciones polinómicas también se pueden definir utilizando polinomios en múltiples variables, como en

.

Funciones polinómicas son una clase importante de funciones suaves.

Ecuaciones polinómicas

Una ecuación polinómica es una ecuación en la que un polinomio se fija igual a otro polinomio.

es una ecuación polinómica.

Propiedades elementales de los polinomios

1. La suma de polinomios es un polinomio
2. La producto de polinomios es un polinomio
3. El derivado de una función polinómica es una función polinómica
4. Cualquier primitivo o primitiva de una función polinómica es una función polinómica

Polinomios sirven para aproximar otras funciones , tales como seno, coseno , y exponencial .

Todos los polinomios tienen una forma expandida, en la que el ley distributiva se ha utilizado para eliminar todos los paréntesis. Todos los polinomios también tienen una forma factorizada en el que el polinomio se escribe como un producto de polinomios lineales. Por ejemplo, el polinomio

es la forma desarrollada del polinomio

,

que está escrito en forma factorizada. Tenga en cuenta que las constantes en los polinomios lineales (como -3 y 1 en el ejemplo anterior) pueden ser números complejos en ciertos casos.

En álgebra escolar, los estudiantes aprenden a moverse fácilmente de una forma a la otra (ver: factoring ).

Cada polinomio en una variable es equivalente a un polinomio con la forma

.

Esta forma se toma a veces como la definición de un polinomio en una variable.

Evaluación de un polinomio consiste en asignar un número a cada variable y la realización de las multiplicaciones y sumas indicadas. La evaluación se realiza a veces de manera más eficiente el uso de la Esquema de Horner

.

En primaria el álgebra , los métodos se dan para resolver todas las ecuaciones polinómicas de primer grado y de segundo grado en una variable. En el caso de ecuaciones polinómicas, la variable es a menudo llamado un desconocido. El número de soluciones no podrá superar el grado, y será equivalente al grado cuando multiplicidad de soluciones y números complejos soluciones se cuentan. Este hecho se llama teorema fundamental del álgebra.

Un sistema de ecuaciones polinómicas es un conjunto de ecuaciones en las que una determinada variable debe tener el mismo valor en todas partes aparece en ninguna de las ecuaciones. Sistemas de ecuaciones se agrupan generalmente con una sola llave de apertura a la izquierda. En álgebra elemental , los métodos se dan para resolver un sistema de ecuaciones lineales en varias incógnitas. Para obtener una solución única, el número de ecuaciones debe ser igual al número de incógnitas. Si hay más incógnitas que ecuaciones, el sistema se denomina underdetermined . Si hay más ecuaciones que incógnitas, el sistema se denomina sobredeterminado. Este importante tema se estudia ampliamente en el área de las matemáticas conocida como álgebra lineal . Sistemas sobredeterminado son comunes en aplicaciones prácticas. Por ejemplo, una encuesta de mapeo estadounidense usó computadoras para resolver ecuaciones 2,5 millones en 400 mil incógnitas.

Ejemplos más avanzadas de polinomios

En álgebra lineal , la polinomio característico de una matriz cuadrada codifica varias propiedades importantes de la matriz .

En la teoría de grafos polinomio cromática de una grafo codifica las diferentes formas de vértice colorear el gráfico usando x colores.

En álgebra abstracta , uno puede definir polinomios con coeficientes en cualquier anillo.

En la teoría de nudos del Alexander polinomio, el Polinomio de Jones, y el HOMFLY polinomio son importantes invariantes de nudos.

Historia

La determinación de las raíces de polinomios, o "la resolución de ecuaciones algebraicas", es uno de los problemas más antiguos de la matemática. Sin embargo, la notación elegante y práctico que utilizamos hoy en día sólo se desarrolló a partir del siglo 15. Antes de eso, las ecuaciones se escriben con palabras. Por ejemplo, un problema de álgebra de los chinos Aritmética en nueve secciones, alrededor del año 200 aC, comienza "Tres gavillas de buena cosecha, dos gavillas de la cosecha mediocre, y una gavilla de mala cosecha se vendió por 29 dou". Escribiríamos .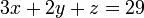

Notación

El primer uso conocido del signo igual es en Robert Recorde La piedra de afilar de Witte, 1557. La signos + para la suma, - para la resta, y el uso de una carta para un desconocido aparece en De Michael Stifel Arithemetica integra, 1544. René Descartes, en La géométrie de 1637, introdujo el concepto de la gráfica de una ecuación polinómica. Él popularizó el uso de las letras desde el principio del alfabeto para denotar constantes y letras de la final del alfabeto para denotar las variables, como se puede ver arriba, en la fórmula general para un polinomio en una variable, donde el un 's denotan constantes y x denota una variable. Descartes introdujo el uso de superíndices para denotar exponentes también.

Resolución de ecuaciones polinómicas

Cada corresponde polinómicas a una función polinómica, donde f (x) se establece igual al polinomio, y una ecuación polinómica, donde el polinomio se fija igual a cero. Las soluciones de la ecuación se llaman las raíces del polinomio y son los ceros de la función y las intersecciones x de su gráfica. Si x = a es una raíz de un polinomio, a continuación, (x - a) es un factor de ese polinomio.

Algunos polinomios, como f (x) = x ² + 1, no tienen ningún arraigo entre los números reales . Si, sin embargo, el conjunto de candidatos permitidos se expande para los números complejos , cada (no constante) polinomio tiene al menos una raíz distinta; esto se desprende de la teorema fundamental del álgebra.

Hay una diferencia entre la aproximación de las raíces y la búsqueda de raíces exactas. Fórmulas para las raíces de polinomios hasta un grado de 2 han sido conocidos desde la antigüedad (ver ecuación de segundo grado ) y hasta un grado de 4 desde el siglo 16 (ver Gerolamo Cardano, Niccolo Fontana Tartaglia). Pero las fórmulas de grado 5 eludieron investigadores. En 1824, Niels Henrik Abel demostró el sorprendente resultado de que no puede haber una fórmula general (que incluye únicamente las operaciones aritméticas y radicales) para las raíces de un polinomio de grado 5 o superior en términos de sus coeficientes (ver Abel-Ruffini teorema). Este resultado marcó el inicio de la teoría de Galois que se dedica a un estudio detallado de las relaciones entre las raíces de los polinomios.

Numéricamente resolver una ecuación polinómica con una incógnita es fácil de hacer en la computadora por el Método Durand-Kerner o por algún otro Resolución numérica de ecuaciones no lineales. La reducción de las ecuaciones en varias incógnitas a las ecuaciones Cada uno en un desconocido se discute en el artículo sobre el El algoritmo de Buchberger. El caso especial en el que todos los polinomios son de grado uno se llama un sistema de ecuaciones lineales , para los que una serie de diferentes métodos de solución existe, incluyendo el clásico de eliminación de Gauss .

Se ha demostrado por Richard Birkeland y Karl Meyr que las raíces de un polinomio cualquiera se pueden expresar en términos de multivariante funciones hipergeométricas. Ferdinand von Lindemann y Hiroshi Umemura mostró que las raíces también se pueden expresar en términos de Siegel funciones modulares, generalizaciones de la funciones theta que aparecen en la teoría de la funciones elípticas. Estas caracterizaciones de las raíces de polinomios arbitrarios son generalizaciones de los métodos previamente descubrió para resolver el ecuación de quinto grado.

Gráficos

Una función polinómica en una variable real puede ser representado por una gráfico.

• La gráfica del polinomio cero

f (x) = 0

es el eje x.

• La gráfica de un grado 0 polinomio

f (x) = a _0, donde a ₀ ≠ 0,

es una línea horizontal con un ₀ y interceptación

• El gráfico de un grado de polinomio 1 (o función lineal)

f (x) = a ₀ + a ₁ x, donde un ₁ ≠ 0,

es una línea oblicua y con una interceptación ₀ y pendiente de un _1.

• La gráfica de un polinomio de grado 2

f (x) = a ₀ + a ₁ x + a ₂ x ^2, donde un ₂ ≠ 0

es un parábola.

• El gráfico de cualquier polinomio con grado 2 o mayor

f (x) = a ₀ + a ₁ x + a ₂ x ² +. . . + A _n x ^n, donde a _n ≠ 0 y n ≥ 2

es una curva no lineal continua.

Gráficos polinómicas se analizan en cálculo utilizando intercepta, pendientes, concavidad, y el comportamiento extremo.

Las ilustraciones siguientes muestran las gráficas de polinomios.

Polinomio de grado 2: f (x) = x 2 - x - 2 = (X 1) (x -2)	Polinomio de grado 3: f (x) = x 3/5 + 4 x 2/5 - 7 x / 5 - 2 = 1/5 (5 x) (x 1) (x -2)
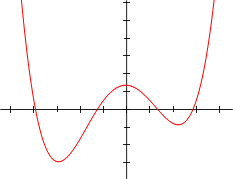Polinomio de grado 4: f (x) = 1/14 (x 4) (x 1) (x-1) (x -3) + 0,5	Polinomio de grado 5: f (x) = 1/20 (x 4) (x 2) (x 1) (x-1) (x -3) + 2

Polinomios y cálculo

Un aspecto importante del cálculo es el proyecto de analizar funciones complicadas por medio de la aproximación con polinomios. La culminación de estos esfuerzos es el teorema de Taylor , que más o menos dice que cada función diferenciable localmente parece un polinomio, y la Teorema de Piedra Weierstrass, que establece que todos los función continua definida en un compacto intervalo del eje real se puede aproximar en todo el intervalo de tan estrechamente como se desee por un polinomio. Los polinomios se utilizan también con frecuencia para interpolar funciones.

Cocientes de polinomios se llaman expresiones racionales, y las funciones que evalúan expresiones racionales se llaman funciones racionales. Funciones racionales son las únicas funciones que se pueden evaluar en un ordenador mediante una secuencia fija de instrucciones que impliquen operaciones de suma, multiplicación, división, que las operaciones con números en coma flotante se implementan normalmente en hardware. Todas las otras funciones que los ordenadores necesitan para evaluar, tales como las funciones trigonométricas , logaritmos y funciones exponenciales , entonces deben ser computado en software que puede utilizar aproximaciones a esas funciones en determinados intervalos de funciones racionales, y posiblemente iteración.

Cálculo de derivadas e integrales de polinomios es particularmente simple. Para el polinomio

la derivada con respecto a x es

y la integral indefinida es

.

Resumen álgebra

En álgebra abstracta , hay que tener cuidado de distinguir entre polinomios y funciones polinómicas. Un polinomio f en una indeterminada 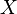sobre anillo se define como la expresión formal de la forma

donde es un número natural, los coeficientes 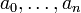son elementos de y X se considera que es un símbolo formal. Dos polinomios que comparten el mismo valor de se considera que son iguales si y sólo si las secuencias de sus coeficientes son iguales; Además, cualquier polinomio es igual a cualquier polinomio con mayor valor de obtenido a partir de ella mediante la adición de términos cuyo coeficiente es cero. Polinomios en 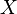con coeficientes en Se pueden añadir simplemente añadiendo correspondientes coeficientes (la regla para extender por términos con coeficientes cero se puede utilizar para hacer que existen de que tales coeficientes). Ellos se pueden multiplicar usando el ley distributiva y el Estado

para todos los elementos a, b del anillo R y todos los números naturales k y l.

Entonces se puede comprobar que el conjunto de todos los polinomios con coeficientes en las propias formas R anillo un anillo, el anillo de los polinomios más de R, que se denota por R [X]. Si R es conmutativo , entonces R [X] es una álgebra sobre R.

Uno puede pensar en el anillo R [X] como el resultado de R añadiendo uno nuevo elemento X a R y sólo requiere que X conmutan con todos los elementos de R. Para que R [X] para formar un anillo, todas las combinaciones lineales de potencias de X tienen que ser incluidos también. La formación del anillo de polinomios, junto con la formación de los anillos de los factores por factorizar ideales, son herramientas importantes para la construcción de nuevos anillos de conocidos. Por ejemplo, la construcción de limpia campos finitos implica el uso de esas operaciones, comenzando con el campo de enteros módulo algún número primo como el anillo coeficiente R (véase aritmética modular ).

Si es conmutativo , entonces se puede asociar a cada polinomio f en , Una función polinómica con dominio y el rango igual a (Más en general uno puede tomar dominio y el rango de ser el mismo unital álgebra asociativa sobre ). Se obtiene el valor de esta función para un argumento dado r mediante la sustitución de todas partes el símbolo X en la expresión f 's por r. Una razón de que algebristas distinguen entre polinomios y funciones polinómicas es que durante algunos anillos de diferentes polinomios pueden dar lugar a la misma función polinómica (ver Pequeño teorema de Fermat para un ejemplo donde R es los enteros módulo p). Este no es el caso cuando son los números reales o complejos y, por tanto, muchos analistas a menudo no se separan los dos conceptos. Una razón aún más importante distinguir entre polinomios y funciones polinómicas es que muchas operaciones en polinomios (como División euclidiana) requiere mirar lo que un polinomio se compone de una expresión en lugar de evaluar en algún valor constante para 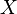. Y debe observarse que si no es conmutativa, no hay (buen comportamiento) noción de función polinómica en absoluto.

Divisibilidad

En álgebra conmutativa, uno de los focos principales de estudio es la divisibilidad entre polinomios. Si R es una dominio yfyg integral son polinomios en R [X], se dice que f divide g si existe un polinomio q en R [X] tal que f q = g. Uno puede entonces mostrar que "cada cero da lugar a un factor lineal", o más formalmente: si f es un polinomio en R [X] y r es un elemento de R tal que f (r) = 0, entonces el polinomio ( X - r) divide f. Lo contrario también es cierto. El cociente se puede calcular utilizando la Esquema de Horner.

Si F es una de campo y f y g son polinomios en F [X] con G ≠ 0, entonces existen polinomios único q y r en F [X] con

y tal que el grado de r es menor que el grado de g. El q polinomios y r están determinados únicamente por f y g. Esto se llama "la división con resto" o " división larga polinómica "y muestra que el anillo F [X] es un Dominio euclidiana.

Análogamente, "primos" polinómicas (más correctamente, polinomios irreducibles) puede ser definido que no se puede factorizar en el producto de dos polinomios de menor grado. No es fácil determinar si un polinomio dado es irreducible. Uno puede comenzar simplemente comprobando si el polinomio tiene factores lineales. Entonces, uno puede comprobar la divisibilidad por algunos otros polinomios irreducibles. El criterio de Eisenstein también se puede utilizar en algunos casos para determinar irreductibilidad.

Ver también: Máximo común divisor de dos polinomios.

Clasificaciones

La clasificación más importante de polinomios se basa en el número de distintas variables. Un polinomio en una variable se llama un polinomio univariado, un polinomio en más de una variable que se llama un polinomio multivariable. Estas nociones se refieren más a la clase de polinomios uno que generalmente se trabaja con que a polinomios individuales; por ejemplo cuando se trabaja con polinomios univariantes uno no excluye polinomios constantes (que pueden resultar por ejemplo de la resta de polinomios no constantes), aunque estrictamente hablando polinomios constantes no contienen ninguna variable en absoluto. Es posible clasificar aún más polinomios multivariados como bivariada, trivariate etc., de acuerdo con el número de variables, pero esto rara vez se hace; es más común, por ejemplo, para decir simplemente "polinomios en x, y, z". A (generalmente mulitvariate) polinomio se llama homogénea de grado n si todos sus términos tienen grado n.

Polinomios univariantes tienen muchas propiedades que no son compartidos por polinomios multivariados. Por ejemplo, los términos de un polinomio univariado están completamente ordenados por su grado, y es convencional para siempre escribirlas en orden decreciente de grado. Un polinomio univariado en x de grado n entonces toma la forma general

donde c _n, c _{n -1,} ..., c _2, c ₁ y c ₀ son constantes, los coeficientes de este polinomio. Aquí el término c _n x ⁿ se llama el término de liderazgo y su coeficiente c _n el coeficiente principal; Si el coeficiente principal es 1, el polinomio mónico univariante se llama. Tenga en cuenta que, aparte del líder coeficiente c _n (que debe ser distinto de cero o de lo contrario el polinomio no sería de grado n) esta forma general permite coeficientes sean cero; cuando esto sucede, el término correspondiente es cero y puede ser removido de la suma sin cambiar el polinomio. Sin embargo, es común referirse a c _i como coeffient de x ^i, incluso cuando c _i pasa a ser 0, de modo que x ⁱ en realidad no ocurre en ningún plazo; por ejemplo, se puede hablar de la término constante del polinomio, es decir, c _0, incluso si debe ser cero.

Los polinomios de manera similar se pueden clasificar por el tipo de valores constantes permitidos como coeficientes. Uno puede trabajar con polinomios con coeficientes enteros, racionales, reales o complejos, y en polinomios álgebra abstracta con se pueden definir muchos otros tipos de coeficientes. Al igual que para la clasificación anterior, se trata de los coeficientes uno está generalmente trabajan; por ejemplo cuando se trabaja con polinomios con coeficientes complejos se incluye polinomios cuyos coeficientes pasar a todos ser real, aunque tales polinomios también pueden ser considerados como un polinomios con coeficientes reales.

Polinomios más se pueden clasificar por su grado y / o el número de términos distintos de cero que contienen.

Polinomios clasificados por grado

Grado	Nombre	Ejemplo
	cero
	(Distinto de cero) constante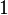
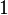	lineal
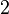	cuadrático
	cúbico
	quartic o bicuadrático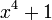
	quintic
	sextic o hexic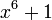
	séptico o heptic
	Octic
	nonic
	Decic

Los nombres de los grados más alta que son menos comunes. Los nombres de los grados se pueden aplicar al polinomio o con sus términos. Por ejemplo, una constante puede referirse a un polinomio de grado cero o un término de cero grados.

El polinomio 0, lo que puede ser considerado no tener en términos de todo, se llama el polinomio cero. A diferencia de otros polinomios constantes, su grado no es cero. Más bien, el grado del polinomio cero o bien se dejó explícitamente indefinido o definido para ser negativo (ya sea -1 o -∞) . Esta última convención es importante para definir División euclidiana de polinomios.

Polinomios clasificados por número de términos distintos de cero

Número de términos distintos de cero	Nombre	Ejemplo
	cero polinomio
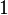	monomio
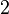	binomio
	trinomio

La palabra monomio puede ser ambigua, ya que también se utiliza a menudo para referirse a un poder de la variable, o en el caso de productos multivariado de tales poderes, sin ningún coeficiente. Dos o más términos que implican el mismo monomio en este último sentido, es decir que sólo se diferencian en el valor de sus coeficientes, que se llaman las mismas condiciones; que se pueden combinar en un solo término mediante la adición de sus coeficientes; si el término resultante tiene coeficiente de cero, puede ser eliminado por completo. La clasificación anterior de acuerdo con el número de términos asume que términos similares se han combinado primero.

Extensiones del concepto de un polinomio

También se habla de polinomios en varias variables, obtenidas tomando el anillo de polinomios de un anillo de polinomios: R [X, Y] = (R [X]) [Y] = (R [Y]) [X]. Estos son de fundamental importancia en geometría algebraica que estudia las simultáneas cero conjuntos de varios de estos polinomios multivariados.

Los polinomios se utilizan con frecuencia para codificar información sobre algún otro objeto. La polinomio característico de un operador de matriz o lineal contiene información acerca del operador valores propios . La polinomio mínimo de una elemento algebraica registra la relación algebraica simple satisfecha por ese elemento.

Otros objetos relacionados estudiados en álgebra abstracta son series formales, que son como los polinomios pero puede tener grado infinito, y la funciones racionales, que son coeficientes de polinomios.