
Ordenador cuántico
Sabías ...
SOS cree que la educación da una mejor oportunidad en la vida para los niños en el mundo en desarrollo también. Apadrinar un niño para hacer una diferencia real.
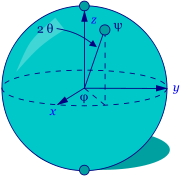
Un ordenador cuántico es un dispositivo para cálculo que hace uso directo del distintivo de la mecánica cuántica fenómenos, tales como superposición y enredo, para realizar operaciones en los datos. En un ordenador clásico (o convencional), la información se almacena como pedacitos; en un ordenador cuántico, se almacena como qubits (qu Antum ts digi narias bi). El principio básico de la computación cuántica es que las propiedades cuánticas se pueden utilizar para representar datos y estructura, y que los mecanismos cuánticos pueden ser concebidos y construidos para realizar operaciones con estos datos.
Aunque la computación cuántica es todavía en su infancia, los experimentos se han llevado a cabo en el que las operaciones computacionales cuántica fueron ejecutados en un número muy pequeño de qubits. Tanto la investigación teórica y práctica sigue con interés, y muchas agencias del gobierno nacional y de financiación militar apoyo a la investigación de la computación cuántica para desarrollar computadoras cuánticas, tanto para fines de seguridad civiles y nacionales, tales como criptoanálisis.
Si los ordenadores cuánticos a gran escala se pueden construir, que será capaz de resolver ciertos problemas mucho más rápido que cualquiera de nuestros ordenadores clásicos actuales (por ejemplo, El algoritmo de Shor). Los ordenadores cuánticos son diferentes de otros ordenadores como Ordenadores de ADN y los ordenadores tradicionales basados en transistores. Algunas arquitecturas de computación, tales como ordenadores ópticos pueden utilizar superposición clásica de ondas electromagnéticas. Sin algunos recursos mecánicos específicamente cuánticos tales como entrelazamiento, se conjetura que una ventaja exponencial en los ordenadores clásicos no es posible.
Base
Un ordenador clásico tiene una memoria integrada por bits, donde cada bit asimientos un uno o un cero. Un ordenador cuántico mantiene una secuencia de qubits. Un solo qubit puede contener un uno, un cero, o, sobre todo, un superposición cuántica de éstos; Por otra parte, un par de qubits pueden estar en una superposición cuántica de 4 estados, y tres qubits en una superposición de 8. En general, un ordenador cuántico con n qubits puede estar en hasta 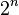 diferentes estados simultáneamente (esto se compara con un ordenador normal que sólo puede estar en uno de estos
diferentes estados simultáneamente (esto se compara con un ordenador normal que sólo puede estar en uno de estos 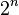 afirma en un momento dado). Un ordenador cuántico opera mediante la manipulación de los qubits con una secuencia fija de puertas lógicas cuánticas. La secuencia de las puertas que se aplicarán se llama un algoritmo cuántico.
afirma en un momento dado). Un ordenador cuántico opera mediante la manipulación de los qubits con una secuencia fija de puertas lógicas cuánticas. La secuencia de las puertas que se aplicarán se llama un algoritmo cuántico.
Un ejemplo de una implementación de qubits para un ordenador cuántico podría comenzar con el uso de partículas con dos girar estados: "arriba" y "abajo" (normalmente escrito  y
y 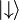 O
O 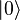 y
y 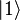 ). Pero, de hecho, cualquier sistema que posee una Una cantidad observable que se conserva bajo evolución en el tiempo y de modo que A tiene al menos dos consecutivos discretas y suficientemente espaciados valores propios , es un candidato adecuado para la implementación de un qubit. Esto es cierto porque cualquiera de tales sistemas puede ser mapeada sobre una efectiva spin-media del sistema.
). Pero, de hecho, cualquier sistema que posee una Una cantidad observable que se conserva bajo evolución en el tiempo y de modo que A tiene al menos dos consecutivos discretas y suficientemente espaciados valores propios , es un candidato adecuado para la implementación de un qubit. Esto es cierto porque cualquiera de tales sistemas puede ser mapeada sobre una efectiva spin-media del sistema.
Bits vs. Qubits
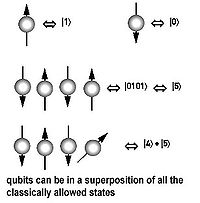
Consideremos en primer lugar un ordenador clásico que funciona en un período de tres bits registrarse. El estado del equipo en cualquier momento es una distribución de probabilidad sobre la  diferentes cadenas de tres bits 000, 001, ..., 111-por lo que se describe por ocho números no negativos (a, b, c, d, e, f, g, h) -Adición de hasta un.
diferentes cadenas de tres bits 000, 001, ..., 111-por lo que se describe por ocho números no negativos (a, b, c, d, e, f, g, h) -Adición de hasta un.
El estado de un ordenador cuántico de tres qubit se describe de manera similar por un vector de ocho dimensiones (a, b, c, d, e, f, g, h), llamado función de onda. Sin embargo, en lugar de añadir a uno, la suma de los cuadrados de las magnitudes de los coeficientes, 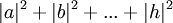 , Debe ser igual a uno. Por otra parte, los coeficientes son números complejos que no tienen por qué ser negativo. El hecho de que los coeficientes pueden ser tanto negativos como positivos permite la cancelación, o interferencia, entre diferentes caminos computacionales, y es una diferencia clave entre la computación cuántica y la computación clásica probabilístico.
, Debe ser igual a uno. Por otra parte, los coeficientes son números complejos que no tienen por qué ser negativo. El hecho de que los coeficientes pueden ser tanto negativos como positivos permite la cancelación, o interferencia, entre diferentes caminos computacionales, y es una diferencia clave entre la computación cuántica y la computación clásica probabilístico.
Si mide los tres qubits, entonces usted va a observar una serie de tres bits. La probabilidad de medir una cadena será igual a la magnitud al cuadrado de los coeficientes de esa cadena. Por lo tanto una medición del estado cuántico con coeficientes (a, b, ..., h) da la distribución de probabilidad clásica 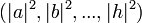 . Nosotros decimos que el estado cuántico "colapsa" a un estado clásico.
. Nosotros decimos que el estado cuántico "colapsa" a un estado clásico.
Tenga en cuenta que un vector de ocho-dimensional puede especificarse de muchas maneras diferentes, dependiendo de lo base que elija para el espacio. La base de cadenas de tres bits 000, 001, ..., 111 que se conoce como la base computacional, y es a menudo conveniente, pero otras bases de unidad de longitud, vectores ortogonales también se pueden utilizar. Notación Ket se utiliza a menudo para hacer explícita la elección de la base. Por ejemplo, el estado (a, b, c, d, e, f, g, h) en la base computacional se puede escribir como 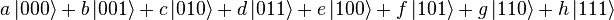 , Donde, por ejemplo,
, Donde, por ejemplo,  = (0,0,1,0,0,0,0,0). La base de cálculo para un único qubit (dos dimensiones) es
= (0,0,1,0,0,0,0,0). La base de cálculo para un único qubit (dos dimensiones) es 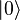 = (1,0),
= (1,0), 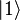 = (0,1), pero otra base común es la base de Hadamard
= (0,1), pero otra base común es la base de Hadamard 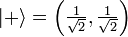 y
y 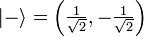 .
.
Tenga en cuenta que si bien la grabación de un estado clásico de n bits, una distribución de probabilidad n-dimensional 2, requiere un número exponencial de los números reales, prácticamente siempre podemos pensar en el sistema como siendo exactamente una de las n -bit cadenas de sólo don ' sé cuál. Cuánticamente, esto ya no es el caso, y los 2 coeficientes n complejas deben mantenerse un registro de ver cómo el sistema cuántico evoluciona. Por ejemplo, un ordenador cuántico de 300 qubit tiene un estado descrito por 2 300 (aproximadamente 10 90) números complejos, más que el número de átomos en el universo observable .
Operación
Mientras que un estado de tres bits clásica y un estado de tres qubits cuánticos son tanto ocho dimensiones vectores, que son manipulados de manera muy diferente para la computación clásica o cuántica, respectivamente. Para computación en cualquier caso, el sistema debe ser inicializado, por ejemplo en la cadena de todos ceros, es decir, (1,0,0,0,0,0,0,0) o 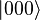 . En el cálculo aleatorio clásica, el sistema evoluciona de acuerdo a la aplicación de matrices estocásticas, que preservan que las probabilidades se suman a uno (es decir, preservar la Norma L1). En computación cuántica, por el contrario, las operaciones permitidas son matrices unitarias, que son efectivamente rotaciones (conservan que la suma de los cuadrados se suman a uno, el Euclidiana o norma L2). (Exactamente lo unitarios se pueden aplicar dependen de la física del dispositivo cuántico.) Por lo tanto, ya que las rotaciones se pueden deshacer girando hacia atrás, los cálculos cuánticos son reversible. (Técnicamente, las operaciones cuánticas pueden ser combinaciones probabilísticas de unitarios, por lo que la computación cuántica realmente tiene generalizar computación clásica. Ver circuito cuántico para una formulación más precisa.)
. En el cálculo aleatorio clásica, el sistema evoluciona de acuerdo a la aplicación de matrices estocásticas, que preservan que las probabilidades se suman a uno (es decir, preservar la Norma L1). En computación cuántica, por el contrario, las operaciones permitidas son matrices unitarias, que son efectivamente rotaciones (conservan que la suma de los cuadrados se suman a uno, el Euclidiana o norma L2). (Exactamente lo unitarios se pueden aplicar dependen de la física del dispositivo cuántico.) Por lo tanto, ya que las rotaciones se pueden deshacer girando hacia atrás, los cálculos cuánticos son reversible. (Técnicamente, las operaciones cuánticas pueden ser combinaciones probabilísticas de unitarios, por lo que la computación cuántica realmente tiene generalizar computación clásica. Ver circuito cuántico para una formulación más precisa.)
Por último, a la terminación del algoritmo, el resultado debe ser leído fuera. En el caso de un ordenador clásico, tomamos muestras de la distribución de probabilidad en el registro de tres bits para obtener una secuencia definida de tres bits, digamos 000. cuánticamente, nos medir el estado de tres qubit, que es equivalente a colapsar el estado cuántico hacia abajo a una distribución clásica (con los coeficientes en el estado clásica siendo las magnitudes cuadráticas de los coeficientes para el estado cuántico, como se describió anteriormente), seguido de muestreo a partir de que la distribución de . Tenga en cuenta que esto destruye el estado cuántico inicial. Muchos algoritmos sólo darán la respuesta correcta con una cierta probabilidad, sin embargo repetidamente inicialización, ejecución y medición de la computadora cuántica, la probabilidad de obtener la respuesta correcta se puede aumentar. Por ejemplo, ejecutar el algoritmo de factorización Shor cuatro veces dará la respuesta correcta con una probabilidad muy alta.
Para más detalles sobre las secuencias de operaciones utilizados para diversos algoritmos, consulte ordenador cuántico universal El algoritmo de Shor, Algoritmo de Grover, Algoritmo de Deutsch-Jozsa, cuántica transformada de Fourier, puerta cuántica, algoritmo cuántico y adiabática corrección de error cuántico.
Potencial
Factorización de enteros se cree que es computacionalmente imposible con una computadora ordinaria para grandes números enteros que son el producto de sólo unos pocos números primos (por ejemplo, productos de dos números primos 300 dígitos). En comparación, un ordenador cuántico podría resolver eficazmente este problema utilizando El algoritmo de Shor para encontrar sus factores. Esta capacidad permitiría a un ordenador cuántico para "romper" muchas de las criptográficos sistemas en uso hoy en día, en el sentido de que no sería un tiempo polinómico (en el número de bits de número entero) algoritmo para resolver el problema. En particular, la mayoría de los populares sistemas de cifrado de clave pública se basan en la dificultad de factorización de enteros (o la relacionada problema del logaritmo discreto que también puede ser resuelto por el algoritmo de Shor), incluyendo las formas de RSA. Estos se utilizan para proteger las páginas seguras Web, correo electrónico cifrado, y muchos otros tipos de datos. Romper estos tendría ramificaciones significativas para la privacidad y la seguridad electrónica. La única manera de aumentar la seguridad de un algoritmo como RSA sería aumentar el tamaño de la clave y la esperanza de que un adversario no tiene los recursos para construir y usar un ordenador cuántico lo suficientemente potente.
Una manera de salir de este dilema sería utilizar algún tipo de criptografía cuántica. Hay también algunos son esquemas de firma digital que se cree que están a salvo de los ordenadores cuánticos. Véase, por ejemplo Firmas de Lamport.
Esta dramática ventaja de los ordenadores cuánticos sólo ha sido descubierta por factorización y discretos logaritmos hasta el momento. Sin embargo, no hay ninguna prueba de que la ventaja es real: un algoritmo clásico igual de rápido todavía puede ser descubierto. Hay otro problema en el que los ordenadores cuánticos tienen una, aunque significativa (cuadrática) ventaja más pequeña. Es de búsqueda de base de datos cuántica, y puede ser resuelto por Algoritmo de Grover. En este caso la ventaja es demostrable. Esto establece fuera de toda duda que (ideal) ordenadores cuánticos son superiores a los ordenadores clásicos para al menos un problema.
Considere la posibilidad de un problema que tiene estas cuatro propiedades:
- La única manera de resolverlo es adivinar respuestas repetidas veces y compruebe ellos,
- Hay n posibles respuestas para comprobar,
- Cada respuesta posible toma la misma cantidad de tiempo para comprobar, y
- No hay pistas acerca de qué respuestas podrían ser mejores: la generación de posibilidades al azar es tan buena como la comprobación de alguna orden especial.
Un ejemplo de esto es una galleta de la contraseña que intenta averiguar la contraseña de una archivo cifrado (suponiendo que la contraseña tiene una longitud máxima posible).
Si tiene problemas con las cuatro propiedades, el tiempo para un ordenador cuántico para resolver este será proporcional a la raíz cuadrada de n (que sería necesario un promedio de (n + 1) / 2 conjeturas de encontrar la respuesta usando un ordenador clásico.) Eso puede ser un gran aumento de velocidad, reducir algunos problemas de años a segundos. Se puede utilizar para atacar cifrados simétricos como Triple DES y AES por intentar adivinar la clave secreta. Independientemente de si alguno de estos problemas pueden ser demostrado tener una ventaja sobre un ordenador cuántico, que, no obstante, siempre tendrán la ventaja de ser una excelente herramienta para el estudio de las interacciones de la mecánica cuántica, que de por sí es un enorme valor para la comunidad científica.
El algoritmo de Grover también se puede utilizar para obtener una velocidad cuadrática-up [más de una búsqueda de fuerza bruta] para una clase de problemas conocidos como NP-completo.
Problemas
Hay una serie de dificultades prácticas en la construcción de un ordenador cuántico, y hasta ahora los ordenadores cuánticos sólo han resuelto los problemas triviales. David DiVincenzo, de IBM, enumeró los siguientes requisitos para que un ordenador cuántico práctico:
- escalable físicamente para aumentar el número de qubits
- qubits se pueden inicializar a valores arbitrarios
- puertas cuánticas más rápido que tiempo de decoherencia
- conjunto universal de puerta
- qubits pueden ser leídos fácilmente
Para resumir los problemas desde la perspectiva de un ingeniero, hay que resolver el reto de construir un sistema que se aísla de todo excepto el mecanismo de medición y manipulación. Además, hay que ser capaz de apagar el acoplamiento de los qubits para la medición de manera que no decoherenciar los qubits mientras realiza operaciones en ellos.
Decoherencia cuántica
Un problema importante es mantener los componentes de la computadora en un estado coherente, como la menor interacción con el mundo exterior podría hacer que el sistema decoherencia. Este efecto hace que el carácter unitario (y más específicamente, la invertibilidad) de pasos computacionales cuántica para ser violado. Tiempos de decoherencia para sistemas candidatos, en particular, el tiempo de relajación transversal T 2 (terminología utilizados en RMN y Tecnología de resonancia magnética, también llamado el tiempo de desfase), suelen oscilar entre nanosegundos y segundos a baja temperatura. La cuestión de enfoques ópticas son más difíciles ya que estas escalas de tiempo son órdenes de magnitud inferior y un enfoque a menudo citado para superar utiliza un enfoque de conformación de impulsos ópticos. Las tasas de error son típicamente proporcional a la relación de tiempo de funcionamiento a tiempo de decoherencia, por lo tanto, cualquier operación debe ser completado mucho más rápidamente que el tiempo de decoherencia.
Si la tasa de error es lo suficientemente pequeño, que se piensa que es posible utilizar la corrección de errores cuántica, que corrige los errores debidos a la decoherencia, permitiendo de ese modo el tiempo total de cálculo a ser más largo que el tiempo de decoherencia. Una cifra a menudo citada (pero bastante arbitrario) para la tasa de error que cada puerta es 10 -4. Esto implica que cada puerta debe ser capaz de realizar su tarea 10.000 veces más rápido que el tiempo de decoherencia del sistema.
El cumplimiento de esta condición de la escalabilidad es posible para una amplia gama de sistemas. Sin embargo, el uso de corrección de errores trae consigo el costo de un gran aumento del número de qubits requeridos. El número requerido para factorizar enteros usando el algoritmo de Shor es todavía polinomio, y se piensa que entre L y L 2, donde L es el número de bits en el número de tenerse en cuenta; algoritmos de corrección de error se infle esta figura por un factor adicional de L. Para un número 1.000 bits, esto implica una necesidad sobre 10 4 qubits sin corrección de errores. Con la corrección de errores, la cifra se elevaría a unos 10 7 qubits. Tenga en cuenta que el tiempo de cálculo es de aproximadamente 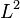 o alrededor
o alrededor  pasos y en 1 M Hz, aproximadamente el 10 segundos.
pasos y en 1 M Hz, aproximadamente el 10 segundos.
Un enfoque muy diferente para el problema de la estabilidad-decoherencia es crear una computadora cuántica topológica con anyons, cuasi-partículas usadas como hilos y que dependen de la teoría de la trenza para formar puertas lógicas estables.
Los candidatos
Hay una serie de candidatos de computación cuántica, entre los que:
- Superconductor equipos basados en cuántica (incluyendo SQUID-basado ordenadores cuánticos)
- Ordenador cuántico de iones atrapados
- Redes ópticas
- Computadora cuántica topológica
- Quantum Dot en la superficie (por ejemplo la Pérdida-DiVincenzo ordenador cuántico)
- La resonancia magnética nuclear de moléculas en disolución (RMN líquido)
- RMN de estado sólido Ordenadores cuánticos Kane
- Los electrones en los ordenadores cuánticos helio
- Electrodinámica cuántica cavidad (CQED)
- Imán molecular
- Basado fullereno- ESR ordenador cuántico
- Ordenadores cuánticos basados en la óptica ( Óptica cuántica)
- Ordenador cuántico basado en Diamante
- Ordenador cuántico de Bose-Einstein basada condensado-
- Cadena ordenadores cuánticos con arrastre de huecos positivos utilizando una trampa electrostática - cuántico equipo basado en transistores
- Ordenador cuántico basado en la vuelta
- Adiabático computación cuántica
El gran número de candidatos muestra explícitamente que el tema, a pesar de un rápido progreso, se encuentra todavía en su infancia. Pero al mismo tiempo hay también una gran cantidad de flexibilidad.
En 2005, investigadores de la Universidad de Michigan construyó un chip semiconductor que funcionaba como un trampa de iones. Tales dispositivos, producidos por la norma técnicas de litografía, pueden señalar el camino a escalables herramientas computación cuántica. Una versión mejorada se hizo en 2006.
La computación cuántica en la teoría de la complejidad computacional
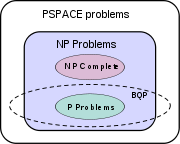
En esta sección se examina lo que actualmente se conoce matemáticamente sobre el poder de los ordenadores cuánticos. En él se describen los resultados conocidos de teoría de la complejidad computacional y la teoría de la computación se trata de ordenadores cuánticos.
La clase de problemas que pueden ser resueltos de manera eficiente por los ordenadores cuánticos se llama PBQ, por "error acotado, cuántica, tiempo polinómico". Los ordenadores cuánticos sólo se ejecutan algoritmos probabilísticos, por lo PBQ en ordenadores cuánticos es la contraparte de BPP en los ordenadores clásicos. Se define como el conjunto de problemas que pueden resolverse con un algoritmo de tiempo polinomial, cuya probabilidad de error está acotado lejos del cuarto. Un ordenador cuántico se dice que "resolver" un problema si, para cada caso, su respuesta va a estar bien con alta probabilidad. Si esa solución se ejecuta en tiempo polinómico, entonces el problema está en PBQ.
BQP está contenida en la clase de complejidad #P (O más precisamente en la clase asociada de problemas de decisión P #P), que es una subclase de PSPACE.
PBQ se sospecha que disjunta de NP-completo y un superconjunto estricto de P, pero que no se conoce. Ambos factorización de enteros y registro discreto están en PBQ. Ambos problemas son problemas NP sospechosos de estar fuera BPP, y por lo tanto fuera de P. Ambos son sospechosos de no ser NP-completo. Hay una idea errónea de que los ordenadores cuánticos pueden resolver los problemas NP-completos en tiempo polinomial. Eso no se sabe para ser verdad, y por lo general se sospecha que es falsa.
Puertas cuánticas pueden ser vistos como transformaciones lineales. Daniel S. Abrams y Seth Lloyd han demostrado que si se permite que las transformaciones no lineales, entonces los problemas NP-completos se pueden resolver en tiempo polinomial. Incluso podría hacerlo por Problemas # P-completo. Ellos no creen que una máquina es posible.
Aunque las computadoras cuánticas pueden ser más rápidos que los ordenadores clásicos, los descritos anteriormente no pueden resolver todos los problemas que los ordenadores clásicos no pueden resolver, dado el tiempo suficiente y la memoria (aunque posiblemente una cantidad que podría prácticamente nunca ponerse en juego). La Máquina de Turing puede simular estos ordenadores cuánticos, por lo que un ordenador cuántico nunca pudo resolver un problema indecidible como el problema de la parada. La existencia de los ordenadores cuánticos "estándar" no refuta la Tesis de Church-Turing.
