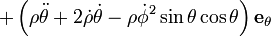Sistema de coordenadas esféricas
Acerca de este escuelas selección Wikipedia
SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Para comparar obras de caridad de patrocinio este es el mejor vínculo de patrocinio .

En matemáticas , el sistema de coordenadas esféricas es un sistema de coordenadas para representar figuras geométricas en tres dimensiones usando tres coordenadas: la distancia radial de un punto de un origen fijo, el ángulo cenital desde el eje z positivo, y el ángulo de azimut del eje x positivo.
Notación
Existen varias convenciones diferentes para la representación de las tres coordenadas. De acuerdo con la Organización Internacional de Normalización ( ISO 31-11), en la física están típicamente anotada como (r, θ, φ) para la distancia radial, cenit, y el acimut, respectivamente.
En (americano) las matemáticas, la notación para cenit y acimut se invierten como φ se utiliza para denotar el ángulo cenital y θ se utiliza para denotar el ángulo azimutal. Una complicación adicional es que algunos de los textos de matemáticas listan el acimut antes del cenit, pero esta convención es zurdo y se debe evitar. La convención "matemáticas" tiene la ventaja de ser más compatible en el sentido de θ con la notación tradicional para el bidimensional sistema de coordenadas polares y el tridimensional sistema de coordenadas cilíndrico, mientras que la convención de la "física" tiene una aceptación más amplia geográficamente. Algunos usuarios de la convención de la "física" también usan φ para coordenadas polares para evitar el primer problema (como es el ISO estándar para coordenadas cilíndricas). Otros notación utiliza ρ para la distancia radial. La convención de notación de autor de cualquier obra relacionada con coordenadas esféricas siempre se debe revisar antes de usar las fórmulas y ecuaciones de ese autor. Este artículo utiliza la convención estándar.
Definición

Las tres coordenadas (r, θ, φ) se definen como:
- r ≥ 0 es la distancia desde el origen a un punto P dado.
- 0 ≤ θ ≤ π es el ángulo entre el eje z positivo y la línea formada entre el origen y P.
- 0 ≤ φ <2π es el ángulo entre el eje x positivo y la línea desde el origen hasta el P proyecta sobre el plano xy.
φ se conoce como el acimut, mientras θ se conoce como el cenit, colatitud o ángulo polar.
θ y φ perder importancia cuando r = 0 y φ pierde importancia cuando el pecado (θ) = 0 (en θ = 0 y θ = π).
Para trazar un punto a partir de sus coordenadas esféricas, vaya unidades r desde el origen a lo largo del eje z positivo, gire θ sobre el eje y en la dirección del eje x positivo y girar φ con respecto al eje z en la dirección de el eje y positivo.
Coordinar las conversiones del sistema
Como el sistema de coordenadas esféricas es sólo uno de los muchos sistemas de coordenadas tridimensionales, existen ecuaciones para la conversión de coordenadas entre el sistema esférico de coordenadas y otros.
Sistema de coordenadas cartesianas
Las tres coordenadas esféricas se obtienen de coordenadas cartesianas por:
Tenga en cuenta que el arcotangente se debe definir de manera adecuada para tener en cuenta el cuadrante correcto de 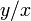 . La atan2 o función equivalente logra esto con fines de cálculo.
. La atan2 o función equivalente logra esto con fines de cálculo.
Por el contrario, las coordenadas cartesianas pueden ser recuperados de coordenadas esféricas por:
Sistema de coordenadas geográficas
El sistema de coordenadas geográficas es una versión alternativa del sistema de coordenadas esféricas, que se utiliza principalmente en la geografía , aunque también en las matemáticas y la física aplicaciones. En geografía, ρ se suele omitir o sustituirá con un valor que representa la elevación o altitud.
Latitud  es el complemento de la cenit o colatitud, y se puede convertir por:
es el complemento de la cenit o colatitud, y se puede convertir por:
 O
O 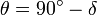 ,
,
aunque latitud se representa típicamente por θ también. Esto representa un ángulo cenital procedente del plano xy con un dominio -90 ° ≤ θ ≤ 90 °. La longitud se mide en grados al este o al oeste de 0 °, por lo que su dominio es -180 ° ≤ φ ≤ 180 °.
Sistema de coordenadas cilíndricas
El sistema cilíndrico de coordenadas es una extrusión de tres dimensiones de la sistema de coordenadas polares , con una coordenada z para describir la altura de un punto por encima o por debajo del plano xy. La tupla completa de coordenadas es (r, φ, z).
Coordenadas cilíndricas se pueden convertir en coordenadas esféricas por:
Coordenadas esféricas se pueden convertir en coordenadas cilíndricas por:
Aplicaciones
La sistema de coordenadas geográficas se aplica a los dos ángulos del esférico sistema para expresar lugares de la Tierra coordinar, llamándolos latitud y de longitud. Así como el de dos dimensiones del sistema de coordenadas cartesianas es útil en el avión, un sistema esférico de coordenadas bidimensional es útil en la superficie de una esfera. En este sistema, la esfera se toma como una esfera unitaria, por lo que el radio es la unidad y generalmente puede ser ignorada. Esta simplificación también puede ser muy útil cuando se trata de objetos tales como matrices de rotación.
Coordenadas esféricas son útiles en sistemas que son simétricos alrededor de un punto de análisis; una esfera que tiene la ecuación cartesiana x 2 + y 2 + 2 z = c 2 tiene la ecuación muy simple r = c en coordenadas esféricas. Un ejemplo es en la resolución de un integral triple con una esfera como su dominio.
El elemento de superficie para una superficie esférica es
El elemento de volumen es
Coordenadas esféricas son las coordenadas naturales para describir y analizar situaciones físicas donde hay simetría esférica, tales como el campo de energía potencial que rodea una esfera (o punto) con la masa o la carga. Dos importantes ecuaciones diferenciales parciales , Y la ecuación de Laplace Ecuación de Helmholtz, permiten una la separación de variables en coordenadas esféricas. Las porciones angulares de las soluciones a tales ecuaciones toman la forma de armónicos esféricos.
Otra aplicación es el diseño ergonómico, donde r es la longitud del brazo de una persona estacionaria y los ángulos de describir la dirección del brazo ya que llega a cabo.
El concepto de coordenadas esféricas se puede extender a los espacios de dimensiones superiores y se hace referencia a continuación como coordenadas hiperesférico.
Cinemática
En coordenadas esféricas se escriba la posición de un punto,
su velocidad es entonces,
y su aceleración es,