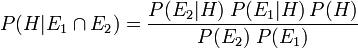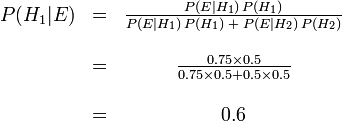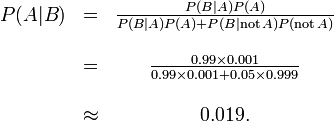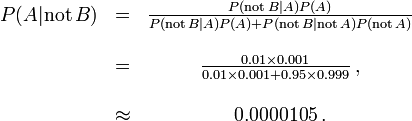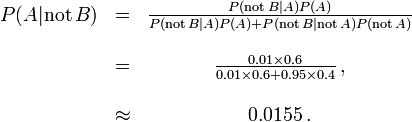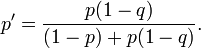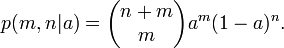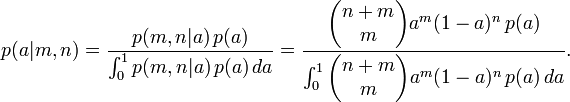Inferência Bayesiana
Sobre este escolas selecção Wikipedia
Esta seleção Escolas foi originalmente escolhido pelo SOS Children para as escolas no mundo em desenvolvimento sem acesso à internet. Ele está disponível como um download intranet. Um link rápido para o patrocínio criança é http://www.sponsor-a-child.org.uk/
Inferência bayesiana é inferência estatística em que provas ou observações são usadas para atualizar ou para recém inferir a probabilidade de que uma hipótese pode ser verdade. O nome "Bayesian" vem do uso freqüente de Teorema de Bayes no processo de inferência. Teorema de Bayes foi derivado do trabalho do Reverendo Thomas Bayes.
Evidências e mudando crenças
Inferência Bayesiana usa aspectos da método científico, que envolve coleta prova de que é feito para ser consistente ou inconsistente com um determinado hipótese. Como evidência se acumula, o grau de crença numa hipótese deveria mudar. Com provas suficientes, deve tornar-se muito alta ou muito baixa. Assim, os proponentes da Inferência Bayesiana dizer que ele pode ser usado para discriminar entre hipóteses conflitantes: com hipóteses muito elevado de apoio deve ser aceita como verdadeira e aqueles com muito pouco apoio deve ser rejeitado como falso. No entanto, os detratores dizem que este método de inferência pode ser tendenciosa devido a crenças iniciais que se deve realizar antes de qualquer prova é sempre recolhida.
Inferência Bayesiana usa uma estimativa numérica do grau de crença em uma hipótese antes foi observada evidência e calcula uma estimativa numérica do grau de crença na hipótese após ter sido observada evidência. Inferência Bayesiana geralmente se baseia em graus de crença, ou probabilidades subjetivas, no processo de indução e não necessariamente pretende fornecer um método objetivo de indução. No entanto, alguns acreditam que os estatísticos Bayesian probabilidades pode ter um valor objetivo e, portanto, inferência bayesiana pode fornecer um método objetivo de indução. Ver método científico.
Teorema de Bayes ajusta probabilidades dadas novas evidências da seguinte maneira:
onde
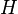 representa uma hipótese específica, que podem ou não ser algumas hipótese nula.
representa uma hipótese específica, que podem ou não ser algumas hipótese nula. 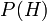 chama-se a probabilidade anterior de
chama-se a probabilidade anterior de 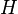 que foi inferida antes de novos elementos de prova,
que foi inferida antes de novos elementos de prova, 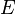 , Tornou-se disponível.
, Tornou-se disponível. 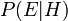 chama-se a probabilidade condicional de ver a evidência
chama-se a probabilidade condicional de ver a evidência 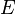 Se a hipótese
Se a hipótese 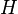 acontece para ser verdade. É também chamado um função de probabilidade quando é considerada como uma função de
acontece para ser verdade. É também chamado um função de probabilidade quando é considerada como uma função de 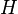 para fixo
para fixo 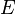 .
.  chama-se a marginal de probabilidade
chama-se a marginal de probabilidade 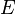 : A probabilidade a priori de testemunhar as novas provas
: A probabilidade a priori de testemunhar as novas provas 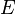 sob todas as hipóteses possíveis. Ela pode ser calculada como a soma do produto de todas as probabilidades de qualquer conjunto completo de hipóteses mutuamente exclusivas e probabilidades condicionais correspondentes:
sob todas as hipóteses possíveis. Ela pode ser calculada como a soma do produto de todas as probabilidades de qualquer conjunto completo de hipóteses mutuamente exclusivas e probabilidades condicionais correspondentes: 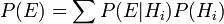 .
.  chama-se a probabilidade posterior de
chama-se a probabilidade posterior de 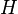 dado
dado 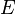 .
.
O factor 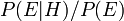 representa o impacto que a prova tem sobre a crença na hipótese. Se é provável que a evidência
representa o impacto que a prova tem sobre a crença na hipótese. Se é provável que a evidência 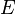 seria observada quando a hipótese em questão é verdade, mas pouco provável que
seria observada quando a hipótese em questão é verdade, mas pouco provável que 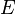 teria sido o resultado da observação, em seguida, este factor será grande. Multiplicando a probabilidade a priori da hipótese por este factor iria resultar numa maior probabilidade posterior da hipótese dada a evidência. Por outro lado, se é provável que a evidência
teria sido o resultado da observação, em seguida, este factor será grande. Multiplicando a probabilidade a priori da hipótese por este factor iria resultar numa maior probabilidade posterior da hipótese dada a evidência. Por outro lado, se é provável que a evidência 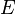 seria observado se a hipótese em questão é verdade, mas um provável priori que
seria observado se a hipótese em questão é verdade, mas um provável priori que 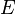 seriam observados, em seguida, o factor reduziria a probabilidade posterior de
seriam observados, em seguida, o factor reduziria a probabilidade posterior de 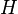 . Sob inferência bayesiana, o teorema de Bayes, portanto, mede a quantidade de novas provas devem alterar uma crença em uma hipótese.
. Sob inferência bayesiana, o teorema de Bayes, portanto, mede a quantidade de novas provas devem alterar uma crença em uma hipótese.
Estatísticos Bayesian argumentam que, mesmo quando as pessoas têm muito diferentes probabilidades subjetivas prévias, novas evidências a partir de observações repetidas tenderá a trazer suas posteriores probabilidades subjetivas mais próximos. No entanto, outros argumentam que quando as pessoas têm muito diferentes subjetiva antes probabilidades suas posteriores probabilidades subjetivas nunca pode convergir mesmo com coleta repetida de provas. Esses críticos argumentam que as visões de mundo que são completamente diferentes, inicialmente, pode permanecer completamente diferente ao longo do tempo, apesar de um grande acúmulo de evidências.
Multiplicando a probabilidade prévia 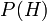 pelo factor
pelo factor 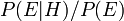 nunca se obter uma probabilidade de que é maior do que 1, desde
nunca se obter uma probabilidade de que é maior do que 1, desde  é pelo menos tão grande quanto
é pelo menos tão grande quanto 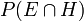 (Onde
(Onde  indica a "e"), o que equivale
indica a "e"), o que equivale 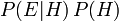 (Veja probabilidade conjunta).
(Veja probabilidade conjunta).
A probabilidade de 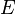 dado
dado 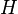 ,
, 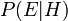 , Pode ser representada como uma função do seu segundo argumento com o seu primeiro argumento mantido fixo. Tal função é chamada um função de verossimilhança; é uma função de
, Pode ser representada como uma função do seu segundo argumento com o seu primeiro argumento mantido fixo. Tal função é chamada um função de verossimilhança; é uma função de 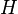 sozinho, com
sozinho, com 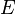 tratado como um parâmetro. Uma razão de duas funções de probabilidade é chamado uma razão de probabilidade,
tratado como um parâmetro. Uma razão de duas funções de probabilidade é chamado uma razão de probabilidade, 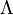 . Por exemplo,
. Por exemplo,
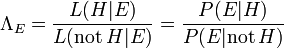 ,
,
onde a dependência de 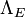 em
em 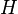 é suprimida para simplicidade (como
é suprimida para simplicidade (como 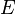 poderia ter sido, exceto teremos de usar esse parâmetro abaixo).
poderia ter sido, exceto teremos de usar esse parâmetro abaixo).
Desde 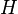 e não-
e não- 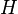 são mutuamente exclusivas e abrangem todas as possibilidades, a soma anteriormente dada para a probabilidade marginal reduz a
são mutuamente exclusivas e abrangem todas as possibilidades, a soma anteriormente dada para a probabilidade marginal reduz a 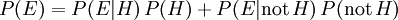 . Como resultado, pode-se reescrever o teorema de Bayes como
. Como resultado, pode-se reescrever o teorema de Bayes como
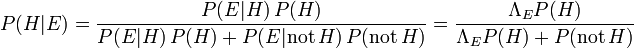 .
.
Poderíamos, então, explorar a identidade 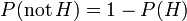 Exibir
Exibir  como uma função de apenas
como uma função de apenas 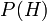 (E
(E 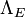 , Que é calculada directamente a partir da evidência).
, Que é calculada directamente a partir da evidência).
Com dois peças independentes de evidência 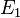 e
e 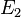 , Inferência Bayesiana pode ser aplicado de forma iterativa. Nós poderíamos usar o primeiro pedaço de evidência para calcular uma probabilidade inicial posterior, e depois usar essa probabilidade posterior como uma nova probabilidade prévia para calcular um segundo probabilidade posterior dado o segundo pedaço de evidência. Teorema de Bayes aplicada de forma iterativa rende
, Inferência Bayesiana pode ser aplicado de forma iterativa. Nós poderíamos usar o primeiro pedaço de evidência para calcular uma probabilidade inicial posterior, e depois usar essa probabilidade posterior como uma nova probabilidade prévia para calcular um segundo probabilidade posterior dado o segundo pedaço de evidência. Teorema de Bayes aplicada de forma iterativa rende
Usando razão de verossimilhança, descobrimos que
![P (H | E_1 \ cap E_2) = \ frac {\ Lambda_1 \ Lambda_2 P (H)} {[\ Lambda_1 P (H) + P (\ mathrm {não} \, H)] \; [\ Lambda_2 P ( H) + P (\ mathrm {não} \, H)]}](../../images/180/18071.png) ,
,
Esta iteração da inferência Bayesiana pode ser estendido com peças mais independentes de evidência.
Inferência bayesiana é usada para calcular as probabilidades para a tomada de decisão sob incerteza. Além das probabilidades, um função de perda deve ser avaliado para ter em conta o impacto relativo das alternativas.
Exemplos simples de inferência Bayesiana
A partir do qual bacia é o biscoito?
Para ilustrar, suponha que há duas taças cheias de cookies. Bacia # 1 tem 10 pedaços de chocolate e 30 biscoitos de deslizamento, enquanto bacia # 2 tem 20 de cada um. O nosso amigo Fred pega uma bacia de forma aleatória, e depois pega um cookie de forma aleatória. Podemos supor que não há razão para acreditar Fred trata uma tigela de forma diferente dos outros, da mesma forma para os cookies. O cookie acaba por ser uma planície. Como provável é que Fred pegou-o para fora da bacia # 1?
Intuitivamente, parece claro que a resposta deve ser mais do que um meio, uma vez que existem biscoitos mais simples na bacia # 1. A resposta precisa é dada pelo teorema de Bayes. Deixar 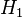 correspondem a bacia # 1, e
correspondem a bacia # 1, e 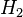 a bacia # 2. É dado que as taças são idênticas do ponto de vista de Fred, assim
a bacia # 2. É dado que as taças são idênticas do ponto de vista de Fred, assim 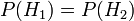 , E os dois devem adicionar-se a 1, então ambos são iguais a 0,5. O evento
, E os dois devem adicionar-se a 1, então ambos são iguais a 0,5. O evento 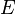 é a observação de um biscoito simples. A partir do conteúdo das tigelas, que sabemos
é a observação de um biscoito simples. A partir do conteúdo das tigelas, que sabemos 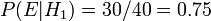 e
e 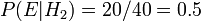 . Fórmula de Bayes, em seguida, produz
. Fórmula de Bayes, em seguida, produz
Antes observamos o cookie, a probabilidade nós atribuímos para Fred tendo escolhido tigela # 1 foi a probabilidade prévia,  , Que foi de 0,5. Depois de observar o cookie, devemos rever a probabilidade de
, Que foi de 0,5. Depois de observar o cookie, devemos rever a probabilidade de  , Que é de 0,6.
, Que é de 0,6.
Falsos positivos em um teste médico
Falsos positivos resultam quando um teste falsamente ou incorretamente relata um resultado positivo. Por exemplo, um exame médico para uma doença pode retornar um resultado positivo indicando que o paciente tem uma doença, mesmo que o paciente não ter a doença. Nós podemos usar o teorema de Bayes para determinar a probabilidade de que um resultado positivo é na verdade um falso positivo. Descobrimos que, se uma doença rara é, em seguida, a maioria dos resultados positivos falsos positivos podem ser, mesmo que o teste é preciso.
Suponha-se que um ensaio para uma doença gera os seguintes resultados:
- Se um doente testado tem a doença, o teste retorna um resultado positivo de 99% do tempo, ou com probabilidade de 0,99
- Se um doente testado não tem a doença, o teste retorna um resultado positivo de 5% do tempo, ou com probabilidade de 0,05.
Ingenuamente, pode-se pensar que apenas 5% dos resultados dos testes positivos são falsas, mas isso é completamente errado, como veremos.
Suponha-se que apenas 0,1% da população tem essa doença, de modo que um paciente seleccionado aleatoriamente tem uma probabilidade de 0,001 antes de ter a doença.
Nós podemos usar o teorema de Bayes para calcular a probabilidade de um resultado positivo do teste é um falso positivo.
Sejam A representa o estado em que o paciente tem a doença, e B representam a prova de um resultado de teste positivo. Então, a probabilidade de que o paciente realmente tem a doença dado o resultado positivo do teste é
e, portanto, a probabilidade de que um resultado positivo é um falso positivo é de cerca de 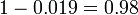 , Ou 98%.
, Ou 98%.
Apesar do aparente alta precisão do teste, a incidência da doença é tão baixa que a grande maioria dos doentes com teste positivo não ter a doença. No entanto, a fração de pacientes com teste positivo que têm a doença (0,019) é de 19 vezes a fracção de pessoas que ainda não tomaram o teste que têm a doença (001). Assim, o teste não é inútil, e re-teste pode melhorar a fiabilidade do resultado.
A fim de reduzir o problema de falsos positivos, o teste deve ser muito preciso em relatar um resultado negativo, quando o paciente não ter a doença. Se o teste geraram um resultado negativo em pacientes sem a doença com probabilidade 0.999, em seguida,
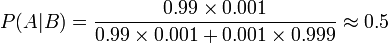 ,
,
de modo que 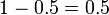 agora é a probabilidade de um falso positivo.
agora é a probabilidade de um falso positivo.
Por outro lado, falsos negativos resultam quando um teste falsamente ou incorretamente relata um resultado negativo. Por exemplo, um exame médico para uma doença pode retornar um resultado negativo, indicando que o paciente não tem uma doença, mesmo que o paciente tenha realmente a doença. Nós também podemos usar o teorema de Bayes para calcular a probabilidade de um falso negativo. No primeiro exemplo acima,
A probabilidade de que um resultado negativo é um falso negativo é de cerca de 0.0000105 ou 0,00105%. Quando uma doença rara, a falsos negativos não ser um grande problema com o teste.
Mas, se 60% da população teve a doença, então a probabilidade de um falso negativo seria maior. Com o teste acima, a probabilidade de um falso negativo seria
A probabilidade de que um resultado negativo é um falso negativo sobe para 0,0155 ou 1,55%.
No tribunal
Inferência Bayesiana pode ser usado em um ajuste da corte por um jurado indivíduo a se acumular de forma coerente as evidências a favor e contra a culpabilidade do réu, e ver se, na totalidade, se encontra com o seu limiar pessoal para "além de uma dúvida razoável".
- Deixar
 denotar o caso em que o réu é culpado.
denotar o caso em que o réu é culpado.
- Deixar
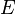 denotar o evento que o DNA do réu corresponde DNA encontrado na cena do crime.
denotar o evento que o DNA do réu corresponde DNA encontrado na cena do crime.
- Deixar
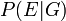 denotar a probabilidade de ver evento
denotar a probabilidade de ver evento 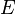 se o réu realmente é culpado. (Normalmente este seria levado para ser a unidade.)
se o réu realmente é culpado. (Normalmente este seria levado para ser a unidade.)
- Deixar
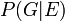 denotar a probabilidade de que o réu é culpado assumindo a partida DNA (evento
denotar a probabilidade de que o réu é culpado assumindo a partida DNA (evento 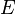 ).
).
- Deixar
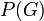 denotar estimativa pessoal do jurado da probabilidade de que o réu é culpado, com base nas provas que não seja o jogo DNA. Isso poderia ser baseado em suas respostas sob questionamento, ou anteriormente apresentado provas.
denotar estimativa pessoal do jurado da probabilidade de que o réu é culpado, com base nas provas que não seja o jogo DNA. Isso poderia ser baseado em suas respostas sob questionamento, ou anteriormente apresentado provas.
Inferência bayesiana nos diz que se pode atribuir uma probabilidade p (G) a culpa do réu, antes de tomar a evidência de DNA em conta, então podemos rever essa probabilidade para a probabilidade condicional 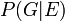 , Desde
, Desde
Suponha-se, com base em outras provas, um jurado decidir que existe uma chance de 30% que o réu é culpado. Suponha também que o testemunho forense foi que a probabilidade de que uma pessoa escolhida aleatoriamente teria DNA que combinava com que na cena do crime é um em um milhão, ou 10 -6.
O evento E pode ocorrer de dois modos. Ou o réu é culpado (com probabilidade prévia 0,3) e, assim, seu DNA está presente com probabilidade 1, ou ele é inocente (com probabilidade prévia 0,7) e ele é azarado o suficiente para ser um dos um em um milhão de pessoas correspondentes.
Assim, o jurado poderia coerentemente rever a sua opinião para ter em conta a Evidência de ADN como se segue:
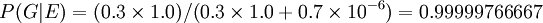 .
.
O benefício da adopção de uma abordagem bayesiana é que dá o jurado um mecanismo formal para combinar as provas apresentadas. A abordagem pode ser aplicada sucessivamente para todos os elementos de prova apresentados em tribunal, com o posterior de um estágio se tornando a prévia para a seguinte.
O jurado ainda teria que ter uma estimativa prévia para a probabilidade de culpa antes do primeiro pedaço de evidência é considerada. Tem sido sugerido que esta poderia razoavelmente ser a probabilidade de uma pessoa culpa aleatória tirada da população de qualificação. Assim, por um crime conhecido por ter sido cometido por um adulto do sexo masculino vivendo em uma cidade contendo 50.000 homens adultos, a probabilidade prévia inicial adequada pode ser 1 / 50.000.

Para o propósito de explicar o teorema de Bayes para júri, será geralmente apropriado para dar-lhe a forma de Apostas ao invés de probabilidades, uma vez que estas são mais amplamente compreendidas. Em teorema de Bayes este formulário 'que
- Odds posteriores = anteriores odds x Fator de Bayes
No exemplo acima, o jurado que tem uma probabilidade anterior de 0,3 para o réu ser culpado seria agora que expressam na forma de uma proporção de 3: 7 em favor do réu sendo culpado, o fator de Bayes é um milhões, eo resultado odds posteriores são 3 milhões para 7 ou cerca de 429 mil para um em favor de culpa.
A abordagem logarítmica que substitui multiplicação com adição e reduz a gama dos números envolvidos pode ser mais fácil para um júri de manusear. Essa abordagem, desenvolvida por Alan Turing durante a Segunda Guerra Mundial e, mais tarde promovido pela IJ Good e ET Jaynes entre outros, eleva-se a utilização de entropia informações.
No Reino Unido, o teorema de Bayes foi explicado ao júri sob a forma chances de um estatístico testemunha especialista no caso de estupro de Regina contra Denis John Adams. A condenação foi garantido, mas o caso foi a recurso, como não há meios de acumular evidências foram fornecidas para os jurados que não querem usar o teorema de Bayes. O Tribunal de Recurso confirmou a condenação, mas também deu sua opinião de que "Para introduzir o teorema de Bayes, ou qualquer método similar, em um julgamento criminal mergulha Júri em reinos impróprios e desnecessários da teoria e da complexidade, desviando-os de sua tarefa própria. " Nenhuma outra apelação foi permitido ea questão da avaliação Bayesian de dados de DNA forense permanece controverso.
Gardner-Medwin argumenta que o critério em que devem basear-se um veredicto em um julgamento criminal não é a probabilidade de culpa, mas sim a probabilidade de as provas, uma vez que o réu é inocente (semelhante a um frequentista p-valor). Ele argumenta que se a probabilidade posterior de culpa deve ser calculado pelo teorema de Bayes, a probabilidade prévia de culpa deve ser conhecido. Isso vai depender de a incidência do crime, que é uma invulgar peça de evidência para considerar em um julgamento criminal. Considere as seguintes proposições:
A: A fatos conhecidos e testemunho poderia ter surgido se o réu é culpado,
B: os fatos conhecidos e testemunho poderia ter surgido se o réu é inocente,
C: O réu é culpado.
Gardner-Medwin argumenta que o júri deveria acreditar em ambos A e não-B, a fim de condenar. A e não-B implica a verdade de C, mas o inverso não é verdadeiro. É possível que B e C são verdadeiros, mas, neste caso, ele argumenta que um júri deve absolver, mesmo sabendo que eles vão estar deixando algumas pessoas culpados em liberdade. Veja também O paradoxo de Lindley.
Outros processos judiciais em que argumentos probabilísticos desempenhado algum papel foram os Howland vai falsificação julgamento, o Caso Sally Clark, eo Lucia de Berk caso.
Teoria Pesquisa
Em maio de 1968, o submarino nuclear dos EUA Scorpion (SSN-589) não conseguiu chegar conforme o esperado em seu porto home de Norfolk, Virginia. A Marinha dos EUA estava convencido de que o navio tinha sido perdido ao largo da costa leste, mas uma extensa pesquisa não conseguiu descobrir o naufrágio. Especialista em águas profundas da Marinha dos EUA, John Craven USN, acreditava que era em outro lugar e ele organizou uma busca sudoeste da Açores com base em uma triangulação aproximado controverso por hidrofones. Ele foi atribuído apenas um único navio, o Mizar, e ele seguiu o conselho de uma empresa de consultoria de matemáticos, a fim de maximizar seus recursos. A metodologia de pesquisa foi aprovado Bayesian. Foram entrevistados comandantes de submarinos experientes para construir hipóteses sobre o que poderia ter causado a perda do Escorpião.
A área de mar foi dividido em quadrículas e uma probabilidade atribuída a cada quadrado, em cada uma das hipóteses, para dar um número de grades de probabilidade, uma para cada hipótese. Estes foram então adicionados em conjunto para produzir uma grelha de probabilidade global. A probabilidade ligado a cada quadrado era então a probabilidade de que o acidente estava naquele quadrado. A segunda grade foi construído com probabilidades que representavam a probabilidade de encontrar com êxito o naufrágio se que eram quadrado a ser pesquisado e os destroços estavam a ser realmente lá. Esta era uma função conhecida da profundidade da água. O resultado da combinação desta grade com a grade anterior é uma grade que dá a probabilidade de encontrar destroços em cada quadrado da grade do mar se fosse para ser pesquisado.
Esta grade mar foi sistematicamente procurado de uma forma que começou com as regiões de alta probabilidade primeira e trabalhou até as regiões de baixa probabilidade últimos. Cada vez que um quadrado da grade foi revistado e encontrado vazio sua probabilidade foi reavaliado usando Teorema de Bayes. Isso, então, forçado as probabilidades de todas as outras quadrículas de ser reavaliada (para cima), também pelo teorema de Bayes. A utilização desta abordagem foi um grande desafio computacional para o tempo, mas foi bem sucedida e, eventualmente, o escorpião foi encontrado cerca de 740 quilômetros a sudoeste da Açores em Outubro do mesmo ano. Suponha que um quadrado da grade tem uma probabilidade p de conter a destruição e que a probabilidade de detectar com sucesso os destroços se ele está lá é q. Se o quadrado é pesquisada e nenhum naufrágio é encontrado, então, pelo teorema de Bayes, a probabilidade revista do naufrágio estar no quadrado é dada por
Exemplos mais matemáticos
Naive Bayes classificador
Ver classificador Naive Bayes.
Distribuição a posteriori do parâmetro binomial
Neste exemplo, considerar o cálculo da distribuição do posterior para o parâmetro binomial. Este é o mesmo problema considerado por Bayes na Proposição 9 de seu ensaio.
Estamos atendendo m observada sucessos e fracassos n observada em um experimento binomial. O experimento pode ser jogar uma moeda, puxando uma bola de uma urna, ou pedir a alguém sua opinião, entre muitas outras possibilidades. O que sabemos sobre o parâmetro (vamos chamá-lo a) é declarada como a distribuição a priori, p (a).
Para um determinado valor de a, a probabilidade de sucesso no m m + n é ensaios
Uma vez que m e n são fixas, e um é desconhecida, esta é uma função de probabilidade para um. De forma contínua do lei da probabilidade total, temos
Para algumas opções especiais de distribuição antes do p (a), o integral pode ser resolvido e o posterior toma uma forma conveniente. Em particular, se p (a) é uma distribuição beta com parâmetros m 0 e n 0, em seguida, a parte posterior é também uma distribuição beta com parâmetros m + m 0 e n 0 + n.
A conjugado antes é uma distribuição antes, tais como a distribuição beta no exemplo acima, o qual tem a propriedade de que a parte posterior é o mesmo tipo de distribuição.
O que é "Bayesian" sobre a Proposição 9 é que Bayes apresentou-o como uma probabilidade para o parâmetro a. Isto é, não só pode um probabilidades de computação para os resultados experimentais, mas também para o parâmetro que os governa, eo mesmo álgebra é usado para fazer inferências de qualquer tipo. Curiosamente, Bayes, na verdade, afirma a sua pergunta de uma forma que pode tornar a ideia de atribuir uma distribuição de probabilidade a um parâmetro aceitável para um frequentista. Ele supõe que uma bola de bilhar é jogado aleatoriamente em uma mesa de bilhar, e que a probabilidade p e q são as probabilidades de que bolas de bilhar subsequentes vão cair acima ou abaixo da primeira bola. Ao fazer o binômio parâmetro a depender de um evento aleatório, ele habilmente escapa um atoleiro filosófica que foi um problema, ele provavelmente não estava mesmo ciente.
Aplicações informáticas
Inferência Bayesiana tem aplicações em inteligência artificial e sistemas especialistas. Técnicas de inferência Bayesiana foram uma parte fundamental da informatizado técnicas de reconhecimento de padrões desde o final dos anos 1950. Há também um crescimento da ligação entre os métodos de Bayesian e à base de simulação de Monte Carlo técnicas desde modelos complexos não pode ser processada de forma fechada por uma análise Bayesiana, enquanto o modelo de estrutura gráfica inerente aos modelos estatísticos, pode permitir algoritmos de simulação eficientes como o Amostragem de Gibbs e outros Metropolis-Hastings esquemas algoritmo. Recentemente inferência Bayesiana ganhou popularidade entre os comunidade phylogenetics por estas razões; aplicações tais como BEAST, MrBayes e P4 permitir que muitos parâmetros demográficos e evolutivas que ser estimados simultaneamente.
Tal como aplicado a classificação estatística, inferência Bayesiana tem sido utilizado nos últimos anos para desenvolver algoritmos para identificar massa não solicitados e-mail spam. As aplicações que fazem uso da inferência Bayesiana para filtragem de spam incluem DSPAM, Bogofilter, SpamAssassin, InBoxer, e Mozilla. Classificação Spam é tratada em mais detalhe no artigo sobre o classificador Naive Bayes.
Em algumas aplicações lógica fuzzy é uma alternativa para inferência Bayesiana. A lógica fuzzy e inferência bayesiana, no entanto, não são matematicamente e semanticamente compatível: Você não pode, em geral, compreender o grau de verdade em lógica fuzzy como probabilidade e vice-versa.