Cónica

Assuntos Relacionados: Matemática

Você sabia ...

Este conteúdo da Wikipedia foi escolhida pela SOS Children para adequação nas escolas de todo o mundo. Todas as crianças disponíveis para apadrinhamento de crianças de Crianças SOS são cuidadas em uma casa de família pela caridade. Leia mais ...

Wikibooks tem um livro sobre o tema de: Cónicas

Tipos de seções cônicas

Tabela de cônicas, Cyclopaedia, 1728

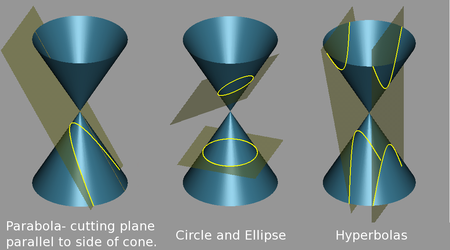
Em matemática , uma secção cónica (ou apenas cónico) é uma curva que pode ser formada por uma intersecção cone (mais precisamente, uma circular à direita superfície cônica) com um avião . As seções cônicas foram nomeados e estudado, já em 200 aC, quando Apolônio de Perga realizou um estudo sistemático de suas propriedades.

Tipos de cônicas

Os cinco tipos de cônicas são do círculo , hipérbole, elipse , parábola, e hipérbole retangular. O círculo ea elipse surgem quando a interseção de cone eo plano é uma curva fechada . O círculo é um caso especial da elipse em que o plano é perpendicular ao eixo do cone. Se o avião está paralela a uma geratriz do cone, a cónica é chamado de uma parábola. Finalmente, se o cruzamento é uma curva aberta e o plano não é paralela às linhas geradoras do cone, a figura é uma hipérbole. (Neste caso, o plano vai intersectar ambas as metades do cone, produzindo duas curvas separadas, embora muitas vezes um é ignorado).

Casos degenerados

Existem vários casos degenerados, em que o plano passa pela vértice do cone. A intersecção, nestes casos, pode ser uma linha recta (quando o avião é tangencial à superfície do cone); um ponto (quando o ângulo entre o plano e o eixo do cone é maior do que isto); ou um par de linhas de intersecção (quando o ângulo é menor). Há também um degenerado em que o cone é uma cilindro (o vértice está no infinito), que pode produzir duas linhas paralelas.

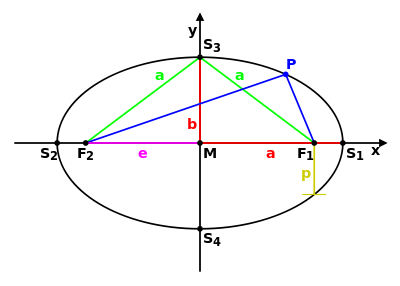
Excentricidade

Elipse (e = 1/2), parábola (e = 1) e hipérbole (e = 2) com focagem fixa F e directriz.

As quatro condições que definem acima podem ser combinadas em uma condição que depende de um ponto fixo F (o foco), uma linha L (directriz) não contendo F e um número real e não negativo (o excentricidade). A secção cónica correspondente consiste em todos os pontos cuja distância é igual a F e vezes o seu raio de L. Para 0 <e <1 obtemos uma elipse, por e = 1 uma parábola, e para e> 1 uma hipérbole.

Para uma elipse e uma hipérbole, pode ser tomado duas combinações foco-Directrix, cada um dando a mesma elipse completa ou hipérbole. A distância a partir do centro para a directriz é $A / E$ , Onde $um \$ é o semi-eixo maior da elipse, ou a distância a partir do centro para os topos da hipérbole. A distância do centro de um foco está $ae \$ .

No caso de um círculo, a excentricidade e = 0, e pode-se imaginar a directriz para ser infinitamente distante do centro. No entanto, a afirmação de que o círculo é composto por todos os pontos cuja distância é e vezes o raio de L não é útil, porque nós temos de zero vezes infinito.

A excentricidade de uma cónica é, portanto, uma medida de quão longe ela se desvia de ser circular.

Para um dado $um \$ , O mais perto $E \$ é 1, a menor é a semi-eixo menor.

Coordenadas cartesianas

No sistema de coordenadas cartesianas , a gráfico de uma equação quadrática em duas variáveis é sempre uma secção cónica, e todas as secções cónicas surgir nesta forma. A equação será de forma

$Ax ^ 2 + Bxy + Cy ^ 2 + Dx + Ey + F = 0 \;$ com $A \$ , $B \$ , $C \$ não todos zero.

em seguida:

se , A equação representa uma elipse (a menos que a cónica é degenerado, por exemplo );
- se $A = C \$ e $B = 0 \$ , A equação representa um círculo ;
se $B ^ 2 - 4AC = 0 \$ , A equação representa um parábola;
se , A equação representa um hipérbole;
- se nós também temos $A + C = 0 \$ , A equação representa um hipérbole retangular.

Note-se que A e B são apenas coeficientes polinomiais, não os comprimentos de semi-eixo maior / menor, conforme definido nas seções anteriores.

Através de mudança de coordenadas essas equações podem ser colocados em formulários:

Circle: $x ^ 2 + y ^ 2 = a ^ 2 \,$
Ellipse: ${X ^ 2 \ over a ^ 2} + {y ^ 2 \ over b ^ 2} = 1 \$ , ${X ^ 2 \ over b ^ 2} + {y ^ 2 \ over a ^ 2} = 1 \$
Parabola: $y ^ 2 = 4AX \, \$
Hipérbole: ${X ^ 2 \ over a ^ 2} - {y ^ 2 \ over b ^ 2} = 1 \$ , ${X ^ 2 \ over a ^ 2} - {y ^ 2 \ over b ^ 2} = - 1 \$
Retangular Hyperbola: $xy = c ^ 2 \$

Tais formas será simétrica sobre o eixo x e para o círculo, elipse e hipérbole simétrica sobre o eixo y.
A hipérbole retangular no entanto só é simétrica sobre as linhas $y = x \$ e $y = -x \$ . Por conseguinte, a sua função inversa é exactamente a mesma que a sua função original.

Estes formulários podem ser escrito como equações paramétricas,

Circle: $(A \ cos \ theta, um \ sin \ theta) \,$ ,
Ellipse: $(A \ cos \ theta, b \ sin \ theta) \,$ ,
Parabola: $(A t ^ 2,2 um t) \,$ ,
Hipérbole: $(A \ s \ theta, b \ \ theta tan) \,$ ou $(\ Pm a \ cosh u, b \ sinh u) \,$ .
Retangular Hyperbola: $(Ct, {c \ over t}) \,$

Coordenadas homogêneas

Em homogénea coordenadas de uma secção cónica pode ser representada como:

$A_1x ^ 2 + A_2y ^ 2 + A_3z ^ 2 + 2B_1xy + 2B_2xz + 2B_3yz = 0.$

Ou na matriz de notação

$\ Begin {bmatrix} x & y & z \ end {} bmatrix. \ Begin {} bmatrix A_1 & B_1 & B_2 \\ B_1 & A_2 & B_3 \\ B_2 & B_3 & A_3 \ end {} bmatrix. \ Begin {} bmatrix x \\ y \\ z \ end {bmatrix} = 0.$

A matriz $M = \ begin {} bmatrix A_1 & B_1 & B_2 \\ B_1 & A_2 & B_3 \\ B_2 & B_3 & A_3 \ end {bmatrix}$ chama-se a matriz da secção cónica.

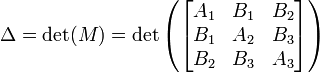$\ Delta = \ det (M) = \ det \ left (\ begin {} bmatrix A_1 & B_1 & B_2 \\ B_1 & A_2 & B_3 \\ B_2 & B_3 & A_3 \ end {bmatrix} \ right)$ é chamado o factor determinante da secção cónica. Se Δ = 0, em seguida, a secção cónica é dito ser degenerado, isto significa que a secção cónica é de facto uma união de duas rectas. Uma seção cônica que corta a si mesmo é sempre degenerada, no entanto nem todos degenerar cónicas cruzam-se, se eles não são linhas retas.

Por exemplo, a secção cónica $\ Begin {bmatrix} x & y & z \ end {} bmatrix. \ Begin {} bmatrix 1 & 0 & 0 \\ 0 & -1 e 0 \\ 0 & 0 & 0 \ end {} bmatrix. \ Begin {} bmatrix x \\ y \\ z \ end {bmatrix} = 0$ reduz-se a união de duas linhas:

$\ {X ^ 2 - y ^ 2 = 0 \} = \ {(x + y) (xy) = 0 \} = \ {x + y = 0 \} \ cup \ {xy = 0 \}$ .

Da mesma forma, uma cónica às vezes se reduz a uma (única) linha:

$\ {X ^ 2 + 2xy + y ^ 2 = 0 \} = \ {(x + y) ^ 2 = 0 \} = \ {x + y = 0 \} \ cup \ {x + y = 0 \} = \ {x + y = 0 \}$ .

$\ Delta = \ det \ left (\ begin {} bmatrix A_1 & B_1 \\ B_1 & A_2 \ end {bmatrix} \ right)$ chama-se a discriminante da seção cônica. Se δ = 0, em seguida, a secção cónica é um parábola, se δ <0, é um hipérbole e se δ> 0, isto é uma elipse . Uma secção cónica é um círculo se δ> 0 e A ₁ = A _2, é uma hipérbole retangular se δ <0 e A = ₁ -A _2. Pode ser provado que, no complexo plano CP projetiva ² duas seções cônicas têm quatro pontos em comum (se é responsável por multiplicidade), de modo que nunca há mais do que 4 pontos de intersecção e há sempre um ponto de interseção (possibilidades: 4 pontos distintos de interseção, dois pontos de intersecção singulares e um pontos de intersecção de casal, 2 pontos de intersecção de casal, 1 singular ponto de intersecção e 1 com multiplicidade de 3 1 ponto de intersecção com a multiplicidade 4). Se existe pelo menos um ponto de intersecção com a multiplicidade> 1, então as duas secções cónicas são referidos como sendo tangente . Se houver apenas um ponto de intersecção, que tem multiplicidade 4, as duas secções cónicas são ditos ser osculating.

Além disso, cada linha reta intercepta cada seção cônica duas vezes. Se o ponto de intersecção é o dobro, a linha é dito ser tangente e é chamado a linha tangente . Porque cada linha reta intercepta uma cónica duas vezes, cada seção cônica tem dois pontos em infinito (os pontos de interseção com a linha no infinito). Se estes pontos são reais, a secção cónica deve ser um hipérbole, se eles são imaginária conjugado, a secção cónica deve ser uma elipse , se a secção cónica tem um duplo ponto no infinito é um parábola. Se os pontos no infinito, são (1, i, 0) e (1, -i, 0), a cónica é um círculo . Se uma seção cônica tem um real e um ponto imaginário no infinito ou que tem dois pontos imaginários que não são conjugados não é nem uma parábola nem uma elipse nem uma hipérbole.

Coordenadas polares

Em coordenadas polares , uma secção cónica com um foco na origem e, se for o caso, a outra sobre o eixo x, é dada pela equação

$r = {l \ over {1 + e \ cos \ theta}}$ ,

onde $e \,$ é a excentricidade e $l \,$ é recto semi-latus (ver abaixo).

Tal como referido acima,

para $e \, = 0$ , Temos um círculo,

para $0 <e \, <1$ obtém-se uma elipse,

para $e \, = 1$ uma parábola,

e para $e \,> 1$ uma hipérbole.

Parâmetros

Vários parâmetros pode ser associada com uma secção cónica.

cónica	equação	excentricidade (e)	excentricidade linear (c)	recto semi-latus (l)	parâmetro focal (p)
círculo	$x ^ 2 + y ^ 2 = r ^ 2 \,$	$0$	$0$	$r \,$	$\ Infty$
elipse	$\ Frac {x ^ 2} {a ^ 2} + \ frac {y ^ 2} {b ^ 2 = 1}$	$\ Frac {\ sqrt {a ^ 2-b ^ 2}} {a}$	$\ Sqrt {a ^ 2-b ^ 2}$	$\ Frac {b ^ 2} {a}$	$\ Frac {b ^ 2} {\ sqrt {a ^ 2-b ^ 2}}$
parábola	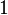$y ^ 2 = 4AX \,$	$1$	$um$	$2a \,$	$2a$
hipérbole	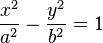$\ Frac {x ^ 2} {a ^ 2} - \ frac {y ^ 2} {b ^ 2 = 1}$	$\ Frac {\ sqrt {a ^ 2 + b ^ 2}} {a}$	$\ Sqrt {a ^ 2 + b ^ 2}$	$\ Frac {b ^ 2} {a}$	$\ Frac {b ^ 2} {\ sqrt {a ^ 2 + b ^ 2}}$

parâmetros cónicas, no caso de uma elipse

Para cada secção cónica, existe um ponto fixo F, uma linha L fixo e um número não-negativo e de tal modo que a secção cónica consiste em todos os pontos cuja distância é igual a F e vezes o seu raio de L. e é chamado o excentricidade da secção cónica.

O excentricidade linear (c) é a distância entre o centro eo foco (ou um dos dois focos).

O latus rectum (2l) é a corda paralela ao directriz e que passa através do foco (ou um dos dois focos).

O recto semi-latus (l) é metade do latus rectum.

O parâmetro focal (p) é a distância a partir do foco (ou um dos dois focos) à directriz.

A relação $p = l / e$ detém.

Propriedades

Cónicas são sempre "suave". Mais precisamente, eles não contêm qualquer pontos de inflexão. Isto é importante para muitas aplicações, tais como aerodinâmica, em que é necessária uma superfície lisa para assegurar fluxo laminar e para evitar turbulência.

Aplicações

Cónicas são importantes na astronomia : o órbitas de dois objetos massivos que interagem de acordo com a lei da gravitação universal de Newton são cónicas se o seu comum centro de massa é considerada em repouso. Se eles estão ligados, ambos irão traçar elipses; se eles estão se movendo à parte, ambos irão seguir parábolas ou hipérboles. Ver problema de dois corpos.

Em geometria projectiva, as secções cónicas no plano projectiva são equivalentes uma à outra até transformações projetivas.

Para aplicações específicas de cada tipo de seção cônica, consulte os artigos círculo , elipse , parábola, e hipérbole.

Interseção duas cônicas

As soluções para um sistema de duas equações de segundo grau em duas variáveis pode ser visto como as coordenadas das interseções de duas seções cônicas genéricos. Em particular dois cônicas podem possuir nenhum, dois, quatro pontos de interseção possivelmente coincidentes. O melhor método para localizar essas soluções é explora o homogénea representação matricial de seções cônicas, ou seja, um 3x3 matriz simétrica que depende de seis parâmetros.

O procedimento para localizar os pontos de intersecção segue estas etapas:

dadas as duas cônicas $C_1$ e $C_2$ Considere o lápis de cônicas dada por sua combinação linear $\ Lambda C_1 + \ mu C_2$
identificar os parâmetros homogéneos $(\ Lambda, \ mu)$ que corresponde à cónica degenerada do lápis. Isto pode ser feito através da imposição de que $det (\ lambda C_1 + \ mu C_2) = 0$ , O que acaba por ser a solução a uma equação de terceiro grau.
dado o cone degenerada $C_0$ , Identificar os dois, possivelmente coincidentes, linhas constituindo-
intercepta cada linha identificada com um dos dois cônica original; este passo pode ser feito de forma eficiente usando a representação cónica dupla de $C_0$
os pontos de intersecção irá representar a solução do sistema de equações inicial

Esferas Dandelin

Ver Esferas Dandelin para um argumento elementar curto mostrando que a caracterização destas curvas como intersecções de um plano com um cone é equivalente à caracterização em termos de focos, ou de um foco e uma diretriz.

Retirado de " http://en.wikipedia.org/w/index.php?title=Conic_section&oldid=206400226 "

Home Page - YouTube Channel