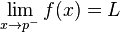Limite de uma função

Em matemática , o limite de uma função é um conceito fundamental no cálculo e análise sobre o comportamento do que função perto de um especial entrada. Informalmente, uma função atribui um saída de f (x) para cada entrada x. A função tem um limite L em uma entrada p se f (x) é "perto" de L sempre que x é "fechar" para p. Em outras palavras, f (x) se tornam cada vez mais perto como L x movimento cada vez mais perto p. Mais especificamente, quando f é aplicada a cada entrada suficientemente perto de p, o resultado é um valor de saída que é arbitrariamente perto de L. Se as entradas "Fechar" para p são levados para os valores que são muito diferentes, o limite é dito que não existe. Definições formais, primeiro elaboradas no início do século 19 , são dadas abaixo.

História

Embora implícita no desenvolvimento do Cálculo dos séculos 17 e 18, a noção moderna de limite de uma função remonta Bolzano que, em 1817, introduziu os conceitos básicos do epsilon-delta técnica. No entanto, seu trabalho não era conhecido durante sua vida. Cauchy discutido limites em seu Cours d'analyse (1821) e parece ter expressa a essência da idéia, mas não de uma forma sistemática. A primeira apresentação pública rigorosa da técnica foi dada por Weierstrass na década de 1850 e 1860 e desde então se tornou o método padrão para lidar com limites.

A notação escrita usando a abreviação lim juntamente com a seta abaixo é devido a Hardy em seu livro Um Curso de Matemática Pura em 1908.

Explicação

Imagine um avião voando sobre uma paisagem representado pelo gráfico de y = f (x). A sua posição horizontal é medido pelo valor de x, bem como a posição dada por um mapa do terreno ou por um sistema de posicionamento global. A sua altura é dada pela coordenada y. Ele está voando para a posição horizontal dada por x = p. Como ele faz isso, ele percebe que a sua altitude aproxima L. Se mais tarde pediu para adivinhar a altitude sobre x = p, seria então responder L, mesmo que nunca tinha realmente chegado a essa posição.

O que significa dizer que a sua altitude aproxima de L? Isso significa que sua altitude fica cada vez mais perto de L, exceto por um possível erro pequeno na precisão. Por exemplo, suponha que definir um objetivo particular precisão para o plano: ele deve chegar dentro de dez metros de L. O avião reporta que ele pode ficar dentro de dez metros de L, uma vez que afirma que quando se está dentro de cinquenta metros horizontais de p, a sua altitude é sempre dez metros ou menos de L.

Nós, então, mudar o nosso objetivo precisão: pode chegar a um metro? Sim. Se estiver dentro de sete metros horizontais de p, em seguida, a sua altitude permanece dentro de um metro do alvo G. Em resumo, para dizer que a altitude do avião se aproxima de L como a sua posição horizontal se aproxima p significa que para cada objetivo precisão alvo, há alguma área de p cuja altitude permanece dentro desse objetivo precisão.

A declaração informal inicial podem agora ser explicada:

O limite de uma função f (x) quando x tende a p é um número L com a seguinte propriedade: dada qualquer distância do alvo a partir de L, há uma distância a partir de p dentro do qual os valores de f (x) permanecem dentro da distância do alvo.

Esta declaração explícita é bastante próxima da definição formal do limite de uma função com valores em um espaço topológico.

Definições

As definições a seguir são os que geralmente aceites para o limite de uma função em vários contextos.

Funções na reta real

Suponha que f: R → R é definida no linha real e p, L ∈ R então dizemos que o limite de f quando x tende a p é L e escrever

se e somente se para cada real ε> 0 existe um verdadeiro δ> 0 tal que 0 <| x - p | <δ implica | f (x) - L | <ε. Note-se que o valor do limite não depende do valor de F (p).

Uma definição mais geral se aplica para funções definidas em subconjuntos da linha real. Seja (a, b) ser um intervalo aberto em R, e p um ponto de (a, b). Seja f uma função real definida em todos (a, b), exceto possivelmente em p. Em seguida, dizer que o limite de f quando x tende a p é L se e somente se, para cada ε reais> 0 existe um δ reais> 0 tal que 0 <| x - p | <δ e x ∈ (a, b ) implica | f (x) - L | <ε. Note-se que o limite não depende de F (p) a ser bem definida.

Limites laterais

Alternativamente x pode aproximar-se p obtido acima (direito) ou abaixo (à esquerda), caso em que os limites podem ser escrito como

ou

respectivamente. Se ambos os limites são iguais a L, então este pode ser referido como o limite de f (x), p. Por outro lado, se não forem ambos iguais a L, em seguida, o limite, como tal, não existe.

Uma definição formal é como se segue. O limite de f (x) quando x tende a p a partir de cima é L se, para cada ε> 0, existe um δ> 0 tal que | f (x) - L | <ε sempre que 0 <x - p <δ. O limite de f (x) quando x tende a p a partir de baixo é L se, para cada ε> 0, existe um δ> 0 tal que | f (x) - L | <ε sempre que 0 <p - x <δ.

Se o limite não existe há um diferente de zero oscilação.

Funções em espaços métricos

Suponha F: (H, d _M) → (N, _N d) é definido entre dois espaços métricos, com x ∈ M, p a ponto limite de M e L ∈ N. Dizemos que o limite de f quando x tende a p é L e escrever

Se e somente se para cada ε> 0 existe um δ> 0 de tal modo que, d _N (f (x), G) <ε sempre que 0 <d _M (x, p) <δ. Novamente, nota que p não necessitam de ser do domínio de f, nem G necessidade de estar na gama de f.

Uma definição alternativa usando o conceito de vizinhança é a seguinte:

Se e somente se para cada vizinhança V de L em N existe uma vizinhança U de p em M, tal que f (L - {p}) ⊆ V.

Funções em espaços topológicos

Suponhamos que X, Y são espaços topológicos com um Y Espaço Hausdorff. Seja p um ponto limite de X, Y e L ∈. Para uma função f: X - {p} → Y, dizemos que o limite de f quando x tende a p é L (isto é, f (x) → L quando x → p) e escrever

Se e somente se para cada vizinhança V de L, existe uma vizinhança U de p tal que f (L - {p}) ⊆ V.

Note-se que o domínio de f não precisam conter p. Se isso acontecer, então o valor de f, p é irrelevante para a definição do limite. A última parte da definição também pode ser formulada "existe uma Módulo: Neighbourhood_ (matemática) ( falar · · hist · Links · subpages · testes - Resultados) L de p tal que f (L) ⊆ V ".

Pode-se formular outras definições semelhantes do limite em um espaço topológico. Numa versão, o domínio da função F é um subconjunto de Ω o espaço topológico X. Neste caso, o ponto p deve ser um ponto limite de Ω, e o limite é tomado com respeito ao topologia induzida em Ω ( limites laterais, onde o limite é tomada dentro de um intervalo em uma das extremidades, são um caso especial deste).

Em particular, se o domínio de f X é - {p} (ou todos X), em seguida, o limite de f quando x → p existe e é igual a L e se apenas se para todos os subconjuntos de Ω X com ponto limite de p o limite da restrição de f para Ω existe e é igual a L. Às vezes, esse critério é usado para estabelecer a não-existência do limite de dois lados de uma função em R mostrando que os limites unilaterais quer deixar de existir ou não concordar. Tal ponto de vista é fundamental no campo da topologia geral, onde limites e continuidade a um ponto são definidos em termos de famílias especiais de subconjuntos, chamado filtros, ou sequências conhecidas como generalizadas redes.

Alternativamente, a exigência de que Y seja um espaço de Hausdorff pode ser relaxada à suposição de que Y seja um espaço topológico geral, mas, em seguida, o limite de uma função não será único. Em particular, não se pode mais falar sobre o limite de uma função em um ponto, mas sim um limite ou o conjunto de limites em um ponto.

Uma função é contínua em um ponto limite de p e no seu domínio e só se F (p) é "a" (ou no caso geral: "a") limite de f (x) quando x tende a p.

Limite de uma função no infinito

O limite desta função no infinito existe.

Se o sistema affinely prorrogado número real (verdadeira linha estendida) R é considerada, ou seja, R ∪ {-∞, + ∞}, então é possível definir limites de uma função no infinito.

Se f (x) é uma função real, em seguida, o limite de f x como se aproxima do infinito é L, denotado

Se e apenas se para todos 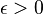existe S> 0 tal que quando x> S.

Da mesma forma, o limite de f quando x tende a infinito é infinito, denotada

Se e somente se para toda a I> 0 existe S> 0 tal que f (x)> R quando x> S.

De forma análoga, os seguintes expressões podem ser definidos:

.

Estas noções de uma tentativa limite para fornecer uma interpretação espaço métrico a limites no infinito. No entanto, note que essas noções de um limite são consistentes com a definição de limite de espaço topológico se

• um bairro de -∞ é definido para conter uma intervalo [-∞, c) onde c ∈ R
• um bairro de ∞ é definido para conter um intervalo (c, ∞], onde R c ∈
• um bairro de uma ∈ R é definido de uma forma normal espaço métrica R

Neste caso, o símbolo R representa um espaço topológico e qualquer função da forma f: X → Y com X, Y ⊆ R é sujeita à definição de um limite topológico. Note-se que com esta definição topológica, que é fácil para definir limites infinitos nos pontos finitos, que não tenham sido definidas acima, no sentido de métrica.

Avaliando limites no infinito para funções racionais

Existem três regras básicas para avaliar os limites no infinito, para uma função racional f (x) = p (x) / Q (X):

• Se o grau de p é maior do que o grau de q, então o limite é infinito positivo ou negativo dependendo dos sinais dos coeficientes principais;
• Se o grau de p e q são iguais, o limite é o coeficiente líder de p dividida pelo coeficiente de levando q;
• Se o grau de p é menor do que o grau de q, o limite é de 0.

. Se o limite no infinito existe, representa uma assíntota horizontal em x = L Polinômios não tem assíntotas horizontais; eles podem ocorrer com funções racionais.

Funções com valor de complexos

O plano complexo com métrica é também um espaço métrico. Existem dois tipos diferentes de limites quando consideramos funções de valor complexo.

Limite de uma função num ponto

Se f é uma função com valor de complexo, em seguida,

se e somente se para todo ε> 0 existe um δ> 0 tal que para todos os números reais x com , Temos .

É apenas um caso particular de funções mais espaços métricos com ambos M e N são o plano complexo.

Limite de uma função de mais de uma variável

De notar que a | x - p | representa um raio, a definição de um limite pode ser estendido para as funções de mais de uma variável. No caso de uma função f: R ² → R,

se e apenas se

para cada ε> 0 existe um δ> 0 de tal modo que para todos (x, y) com 0 <|| (x, y) - (p, q) || <δ, dispomos de | f (x, y) - L | <ε

|| em que (x, y) - (p, q) representa o || Distância euclidiana. Isto pode ser estendido a qualquer número de variáveis.

Propriedades

Para dizer que o limite de uma função f em p é L é equivalente a dizer

para cada seqüência convergente (x _n) em M com limite igual a p, a sequência (f (x _n)) converge com limite L.

Se os conjuntos de A, B, ... formar uma partição finita do domínio função, 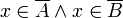, ... E o limite relativo para cada um desses conjuntos a existir e é igual a, por exemplo, L, então existe o limite para o ponto x e é igual a L.

A função f é contínua em p se e somente se o limite de f (x) quando x tende a p existe e é finito. Equivalentemente, f transforma cada sequência em M que converge para p em uma sequência em N que converge em direcção F (p).

Mais uma vez, se N for um espaço vectorial normalizado, em seguida, a operação de limite é linear no seguinte sentido: se o limite de f (x) quando x tende a p é L e o limite de g (x) quando x tende P é P, em seguida, o limite de f (x) + g (x) quando x tende a p é L + P. Se a é um escalar da base campo, então o limite de af (x) quando x tende a p é aL.

Tomando o limite de funções é compatível com as operações algébricas, desde que os limites para os lados da identidade existem certas abaixo:

(O último, desde que o denominador é diferente de zero). Em cada um dos casos acima, quando os limites do lado direito não existir, ou, no último caso, quando os limites em que o numerador e denominador são iguais a zero, no entanto, o limite do lado esquerdo ainda pode existir - depende de qual funções F e G são.

Estas regras também são válidas para limites de um lado, para o caso p = ± ∞, e também para limites infinitos usando as regras

• q + ∞ = ∞ para q ≠ -∞
• q × ∞ = ∞ se q> 0
• q = × ∞ -∞ se q <0
• q / ∞ = 0 se q ≠ ± ∞

(Veja alargado linha número real).

Note-se que não existe uma regra geral para o caso q / 0; tudo depende da forma como é abordada 0. Formas indeterminadas - por exemplo, 0/0, 0 × ∞, ∞-∞ e ∞ / ∞ - também não são abrangidas por essas regras, mas os limites correspondentes podem frequentemente ser determinado com A regra de L'Hôpital ou o Esprema teorema.