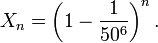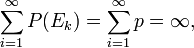Teorema del mono infinito
Antecedentes
Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. SOS Children trabaja en 45 países africanos; puede ayudar a un niño en África ?

El teorema del mono infinito establece que un mono golpeando las llaves en azar en un teclado de máquina de escribir para un cantidad infinita de tiempo es casi seguro que escriba un texto elegido en particular, como las obras completas de William Shakespeare . En este contexto, " casi con toda seguridad "es un término matemático con un significado preciso, y el" mono "no es un mono real, sino que es una metáfora de un dispositivo abstracto que produce una secuencia aleatoria de letras ad infinitum. El teorema ilustra los peligros de razonamiento sobre el infinito imaginando un gran número pero finita, y viceversa. La probabilidad de un mono escribiendo una cadena dada de texto, siempre y cuando, por ejemplo, Hamlet, es tan pequeña que, se llevaron a cabo el experimento, la posibilidad de que realmente se produzca durante un lapso de tiempo del orden de la edad del universo es minúscula pero no cero.
Las variantes del teorema incluyen múltiples e incluso infinitamente muchos mecanógrafos, y el texto de destino varía entre una biblioteca entera y una sola frase. La historia de estos estados se remonta a Aristóteles Metafísica 's y De natura deorum de Cicerón, a través de Blaise Pascal y Jonathan Swift, y, finalmente, a las declaraciones modernas con sus máquinas de escribir icónicas. En el siglo 20, Émile Borel y Arthur Eddington utiliza el teorema para ilustrar los plazos implícitos en los fundamentos de la mecánica estadística . Vario Apologistas cristianos, por una parte, y Richard Dawkins, por otro, han argumentado acerca de la idoneidad de los monos como una metáfora de la evolución .
Hoy en día, el interés popular en los monos de mecanografía es sostenida por numerosas apariciones en la literatura, la televisión y la radio, música e Internet. En 2003, un experimento humorístico se realizó con seis Célebes Crested macacos, pero su contribución literaria era de cinco páginas que consisten en gran parte de la letra S.
Solución
Prueba directa
Hay una prueba sencilla de este teorema. Si dos eventos son estadísticamente independientes, (es decir, ni afecta el resultado de la otra), entonces la probabilidad de suceso tanto es igual al producto de las probabilidades de cada uno de ellos ocurriendo de forma independiente. Por ejemplo, si la probabilidad de lluvia en Sydney en un día en particular es de 0,3 y la posibilidad de un terremoto en San Francisco en ese día es de 0.008, entonces la probabilidad de que tanto sucediendo en ese mismo día es de 0,3 × 0,008 = 0,0024.
Supongamos que la máquina de escribir tiene 50 teclas, y la palabra que ser escrito es " banana ". Typing al azar, la probabilidad de que la primera letra escrita es b es 1/50, y la probabilidad de que la segunda letra escrita es un es también 1/50, y así sucesivamente, porque los eventos son independientes. Así que la probabilidad de el plátano primeras seis letras a juego es
- (1/50) x (1/50) x (1/50) x (1/50) x (1/50) x (1/50) = (1/50) 6.
Por la misma razón, la posibilidad de que los próximos 6 cartas coinciden plátano es también (1/50) 6, y así sucesivamente.
A partir de lo anterior, la posibilidad de no escribir plátano en un bloque dado de 6 letras es 1 - (1/50) 6. Debido a que cada bloque se escribe de forma independiente, la posibilidad X n de no escribir plátano en cualquiera de los n primeros bloques de 6 letras es
Como n crece, X n se hace más pequeño. Para un n de un millón, X n es 99,99%, pero para un n de 10 mil millones de X n es 53% y para un n de 100 mil millones es 0,17%. Como n tiende a infinito, la probabilidad X n se aproxima a cero; es decir, haciendo n suficientemente grande, X n puede hacerse tan pequeña como se quiera.
El mismo argumento se muestra por qué al menos uno de un número infinito de monos (casi seguro) producir un texto tan rápido como sería producido por un mecanógrafo humano perfectamente preciso copiarlo de la original. En este caso X n = (1 - (1/50) 6) n donde n X representa la probabilidad de que ninguno de los primeros tipos n monos plátano correctamente en su primer intento. Cuando consideramos 100 mil millones de monos, la probabilidad cae al 0,17%, y el número de monos que n aumenta hasta el infinito el valor de X n - la probabilidad de que los monos en su defecto para reproducir el texto dado - disminuye a cero. Esto equivale a decir que la probabilidad de que uno o más de un número infinito de monos producirá un texto dado en el primer intento es de 100%, o que es casi seguro que lo hará.
Infinitas cadenas
Las dos afirmaciones anteriores se puede afirmar de forma más general y de forma compacta en términos de cuerdas, que son secuencias de caracteres elegidos de algún alfabeto finito:
- Dada una cadena infinita donde se elige cada personaje uniformemente al azar, cualquier cadena finita dado casi seguramente se produce como subcadena en alguna posición (y, de hecho, un número infinito de posiciones).
- Dada una secuencia infinita de cadenas infinitas, cuando se elija cada carácter de cada cadena uniformemente al azar, cualquier cadena finita dado casi seguramente se produce como un prefijo de una de estas cadenas (y, de hecho, como un prefijo de un número infinito de estas cadenas en el secuencia).
Ambos siguen fácilmente de la segunda Borel-Cantelli lema. Para el segundo teorema, sea E k sea la caso de que el k-ésimo cadena comienza con el texto dado. Debido a que este tiene cierta probabilidad fija p distinto de cero de ocurrir, la E k son independientes, y la suma a continuación diverge,
la probabilidad de que un número infinito de la E k ocurre es 1. El primer teorema se muestra de manera similar; uno puede dividir la cadena aleatoria en bloques no solapados que coinciden con el tamaño del texto deseado, y hacer E k el evento donde el k ésimo bloque es igual a la cadena deseada.
Probabilidades
Ignorando puntuacion, el espaciado y la capitalización, a las letras de mecanografía mono uniformemente al azar tiene la posibilidad de uno de cada 26 de escribir correctamente la primera letra Hamlet. Tiene una probabilidad de una en 676 (26 × 26) de escribir las dos primeras letras. Debido a que la probabilidad se reduce de forma exponencial , al 20 cartas que ya sólo tiene una probabilidad de uno en 26 20 = 19,928,148,895,209,409,152,340,197,376, más o menos equivalente a la probabilidad de comprar 4 billetes de lotería consecutivos y ganar el premio mayor cada vez. En el caso de todo el texto de Hamlet, las probabilidades son tan sumamente pequeñas que apenas pueden ser concebidos en términos humanos. Digamos que el texto de Hamlet contiene 130.000 cartas (en realidad es más, incluso despojado de puntuacion), entonces hay una probabilidad de uno en 3.4 × 10 183 946 para obtener el derecho de texto en el primer juicio. El número medio de cartas que necesita ser escrito hasta que aparezca el texto es también 3,4 × 10 183946.
Para fines de comparación, sólo hay alrededor de 3 × 10 79 átomos de hidrógeno en el universo observable y sólo han transcurrido 4,3 × 10 17 segundos desde el Big Bang . Incluso si el universo observable se llenaron de monos escribiendo para todos los tiempos, su probabilidad total para producir una sola instancia de Hamlet todavía sería menos de uno de cada 10 183800. Como Kittel y Kroemer dijo, "Por tanto, la probabilidad de que Hamlet es cero en cualquier sentido operacional de un evento ...", y la declaración de que los monos deben eventualmente tener éxito "da una conclusión engañosa sobre muy, muy grandes números". Esto es de su libro de texto sobre la termodinámica , el campo cuyos fundamentos estadísticos motivado las exposiciones primera conocidas de monos escribiendo.
Historia
La mecánica estadística
En una de las formas en que los probabilistas ahora conocen este teorema, con su "dactylographic" [es decir, mecanografía] monos ( francés : singes dactylographes; la palabra singe francés cubre tanto los monos y los simios ), aparecieron en 1913 El artículo de Émile Borel "Mécanique Statistique et Irréversibilité" ( mecánica estadística y la irreversibilidad), y en su libro "Le Hasard" en 1914. Sus "monos" no son monos reales; más bien, son una metáfora de una manera imaginaria para producir un gran, secuencia aleatoria de letras. Borel dijo que si un millón de monos escriben diez horas al día, que era muy poco probable que su producción sería exactamente igual todos los libros de las bibliotecas más ricas del mundo; y, sin embargo, en comparación, era aún más improbable que las leyes de la mecánica estadística jamás serían violados, aunque sea brevemente.
El físico Arthur Eddington basó en la imagen de Borel más en La naturaleza del mundo físico (1928), escribiendo:
Si dejo que mis dedos vagan ociosamente sobre las teclas de una máquina de escribir, puede suceder que mi regla realizó una frase inteligible. Si un ejército de monos fueron rasgueando en máquinas de escribir que podría escribir todos los libros en el Museo Británico. La posibilidad de que lo hagan es decididamente más favorable que la probabilidad de las moléculas que regresan a la mitad de la embarcación.
Estas imágenes invitan al lector a considerar la increíble improbabilidad de un número grande pero finito de monos de trabajo para una cantidad grande pero finito de tiempo la producción de una obra significativa, y comparar esto con la mayor improbabilidad de que ciertos eventos físicos. Cualquier proceso físico que es aún menos probable que el éxito esos monos es prácticamente imposible, y puede decirse con seguridad que este proceso nunca va a suceder.
Orígenes y "La Biblioteca Total"
En un ensayo de 1939 titulado "La biblioteca total", el escritor argentino Jorge Luis Borges trazó el concepto de infinito-mono de nuevo a Aristóteles Metafísica 's. Al explicar los puntos de vista de Leucipo, quien sostuvo que el mundo surgió a través de la combinación aleatoria de átomos , Aristóteles señala que los propios átomos son homogéneas y sus posibles acuerdos sólo se diferencian en la posición y el pedido. El filósofo griego compara esto con la forma en que una tragedia y una comedia consisten en los mismos "átomos", es decir, los caracteres alfabéticos. Tres siglos más tarde, De Cicerón natura deorum (Sobre la naturaleza de los dioses) argumentó en contra de la cosmovisión atomista:
El que cree que esto puede creer también que si una gran cantidad de los de uno y veintidós letras, compuestas ya sea de oro o cualquier otro asunto, fueron lanzados sobre la tierra, que caería en el orden que forma legible para formar los Anales de Ennio. Dudo que la fortuna podía hacer un solo verso de ellos.
Borges sigue la historia de este argumento a través de Blaise Pascal y Jonathan Swift, a continuación, que en su propio tiempo, el vocabulario había cambiado. Para 1939, el idioma era "que media docena de monos provistos de máquinas de escribir serían, en pocos eternidades, producir todos los libros en el Museo Británico." (A lo que Borges añade: "En sentido estricto, un mono inmortal sería suficiente.") Borges imagina entonces el contenido de la biblioteca total que esta empresa produciría si se lleva a su máximo extremo:
Todo estaría en sus volúmenes ciegos. Todo: la historia detallada del futuro, de Esquilo Los egipcios, el número exacto de veces que las aguas del Ganges han reflejado el vuelo de un halcón, el carácter secreto y verdadero de Roma, la enciclopedia Novalis habría construido, mis sueños y medias sueños en la madrugada del 14 de agosto de 1934, la demostración del teorema de Pierre Fermat, los capítulos no escritas de Edwin Drood, esos mismos capítulos traducidos a la lengua hablada por los Garamantes, las paradojas Berkeley inventaron relativa Tiempo, pero no publicaron, Los libros de Urizen de hierro, las epifanías prematuros de Stephen Dedalus, que sería sin sentido ante un ciclo de mil años, el evangelio gnóstico de Basílides, el canto de las sirenas cantaban, el catálogo completo de la biblioteca, la prueba de la inexactitud de que catálogo. Todo: pero por una línea razonable o hecho precisa no habría millones de cacofonías sin sentido, farragoes verbales y balbuceos. Todo: pero todas las generaciones de la humanidad podrían pasar antes de las vertiginosas estantes estantes que arrasan el día y en la que el caos mentiras nunca recompensarlos con una página tolerable.
Concepto de biblioteca total Borges fue el tema principal de su muy leída 1941 de cuentos " La biblioteca de Babel ", que describe un inimaginablemente vasta biblioteca que consta de enclavamiento cámaras hexagonales, junto conteniendo cada volumen posible que podría estar compuesto de las letras del alfabeto y algunos signos de puntuación.
Aplicaciones y Críticas
Evolución

En su libro de 1931 El Universo Misterioso, el rival de Eddington James Jeans atribuyen la parábola mono a un "Huxley", refiriéndose probablemente Thomas Henry Huxley. Esta atribución es incorrecta. Hoy en día, a veces se informó además de que Huxley aplica el ejemplo de un ahora legendario debate sobre Charles Darwin 's Origen de las especies con el obispo anglicano de Oxford, Samuel Wilberforce, que tuvo lugar en una reunión de la Asociación Británica para el Avance de la Ciencia en Oxford en 30 de junio de 1860. Esta historia no sólo sufre de una falta de pruebas, pero el hecho de que en 1860 la propia máquina de escribir aún tenía que emerger. Primates eran todavía un tema delicado por otros motivos, y el debate Huxley-Wilberforce hicieron incluir byplay sobre simios: el obispo le preguntó si Huxley era descendiente de un simio en respondieron su lado de su abuelo de la abuela o, y Huxley algo en el sentido que lo haría más bien descender de un simio que de alguien que sostenía como deshonesta como el obispo.
A pesar de la confusión inicial, los argumentos mono-y-máquina de escribir son ahora comunes en las discusiones sobre la evolución. Por ejemplo, Doug Powell argumenta como Apologista cristiano que incluso si un mono accidentalmente tipos de las letras de Hamlet, se ha logrado producir Hamlet porque carecía de la intención de comunicar. Su implicación en paralelo es que las leyes naturales no podían producir la información contenida en el ADN . Un argumento más común es representado por John MacArthur, que afirma que las mutaciones genéticas necesarias para producir una tenia de una ameba son tan improbable como un mono tecleando el soliloquio de Hamlet, y por lo tanto las probabilidades en contra de la evolución de toda la vida son imposibles de superar.
El biólogo evolucionista Richard Dawkins emplea el concepto mono escribiendo en su libro de 1986 El relojero ciego para demostrar las capacidades de la selección natural en la producción biológica complejidad de azar mutaciones. En el experimento de simulación que describe, Dawkins tiene su Programa Weasel producir la frase de Hamlet me parece que es como un COMADREJA escribiendo frases aleatorias pero constantemente congelar las partes de la producción que ya se han encontrado la meta. El punto es que la generación de cadena aleatoria sólo sirve para suministrar las materias primas, mientras que la selección imparte la información.
Una avenida diferente para rechazar la analogía entre la evolución y un mono sin restricciones radica en el problema de que los tipos de monos sólo una letra a la vez, con independencia de las otras letras. Hugh Petrie sostiene que se requiere una configuración más sofisticada, en su caso no por la evolución biológica, pero la evolución de las ideas:
Con el fin de obtener la analogía correcta, habría que dotar al mono con una máquina de escribir más compleja. Se tendría que incluir frases y pensamientos isabelinos enteros. Se tendría que incluir creencias isabelinas sobre los patrones humanos de acción y las causas, la moral isabelina y la ciencia, y los patrones lingüísticos para expresar estos. Probablemente ni siquiera tendría que incluir una descripción de los tipos de experiencias que dieron forma a la estructura de creencias de Shakespeare como un ejemplo particular de un isabelino. Entonces, tal vez, podríamos permitir que el mono de jugar con una máquina de escribir tal y producir variantes, pero la imposibilidad de obtener una obra de Shakespeare ya no es evidente. ¿Qué es variada realmente encapsular una gran cantidad de conocimientos ya alcanzados.
James W. San Valentín, aunque admitió que la tarea del mono clásico es imposible, encuentra que hay una analogía entre la pena Inglés escrito y el metazoos genoma en este otro sentido: ambos tienen ", estructuras jerárquicas combinatorias" que limitan en gran medida el inmenso número de combinaciones a nivel alfabeto.
Teoría de la Literatura
RG Collingwood argumentó en 1938 que el arte no puede ser producido por accidente, y escribió como un sarcástico a un lado a sus críticos,
... Algunos ... han negado esta afirmación, señalando que si un mono juega con una máquina de escribir ... que produciría ... el texto completo de Shakespeare. Cualquier lector que no tiene nada que hacer puede entretenerse calculando cuánto tiempo se necesita para que la probabilidad de que vale la pena apostar por. Pero el interés de la propuesta radica en la revelación del estado mental de una persona que puede identificar las "obras" de Shakespeare con la serie de letras impresas en las páginas de un libro ...
Nelson Goodman tomó la posición contraria, ilustrando su punto junto con Catalina Elgin por el ejemplo de Borges " Pierre Menard, autor del Quijote ",
Lo escribió Menard es simplemente otra inscripción del texto. Cualquiera de nosotros puede hacer lo mismo, como imprentas lata y fotocopiadoras. De hecho, se nos dice, si un número infinito de monos ... uno eventualmente producirían una réplica del texto. Esa réplica, mantenemos, sería tanto una instancia de la obra, Don Quijote, como manuscrito de Cervantes, el manuscrito de Menard, y cada copia del libro que alguna vez haya sido o pueda ser impreso.
En otro escrito, Goodman elabora, "que el mono pueda suponerse que han producido su copia hace al azar ninguna diferencia. Es el mismo texto, y está abierto a todos las mismas interpretaciones ...". Gérard Genette rechaza el argumento de Goodman como petición de principio.
Para Jorge JE Gracia, la cuestión de la identidad de los textos lleva a una pregunta diferente, el de autor. Si un mono es capaz de escribir Hamlet, a pesar de tener la menor intención de significado y, por tanto, descalificando a sí mismo como un escritor, entonces parece que los textos no requieren autores. Las soluciones posibles son diciendo que todo el que encuentra el texto y lo identifica como Hamlet es el autor; o que Shakespeare es el autor, el mono de su representante, y el buscador simplemente un usuario del texto. Estas soluciones tienen sus propias dificultades, en que el texto parece tener un significado distinto de los otros agentes: ¿y si el mono opera antes de que nazca Shakespeare, o si Shakespeare nunca nace, o si nadie encuentra mecanografiado del mono?
Generación de números aleatorios
El teorema se refiere a una pensado experimento que no puede llevarse a cabo totalmente en la práctica, ya que se prevé que requerir cantidades prohibitivas de tiempo y recursos. No obstante, se ha inspirado esfuerzos en la generación finita texto aleatorio.
Un programa informático dirigido por Dan Oliver de Scottsdale, Arizona, según un artículo publicado en The New Yorker, se acercó con un resultado el 4 de agosto, 2004: Después de que el grupo había trabajado para 42,162,500,000 millones de millones de años, uno de los "monos" con tipo, "SAN VALENTÍN. Cese toIdor: eFLP0FRjWK78aXzVOwm) - '; 8.t. . ". Los primeros 19 cartas de esta secuencia se pueden encontrar en" Los dos hidalgos de Verona ". Otros equipos han reproducido 18 personajes de" Timón de Atenas ", 17 de" Troilo y Crésida ", y 16 de" Ricardo II ".
Un sitio web titulado El mono Shakespeare Simulator, puesto en marcha en 1 de julio de 2003 , contenía una Applet de Java que simula una gran población de monos escribiendo al azar, con la intención declarada de ver cuánto tiempo le toma a los monos virtuales para producir una obra de Shakespeare completa de principio a fin. Por ejemplo, se produce esta línea parcial de Enrique IV, Parte 2, informando que se tomó "2.737.850 millones de billones de billones de billones de mono-año" para llegar a 24 caracteres coincidentes:
- RUMOR. Abran sus oídos; 9r "5j5 & OWTY Z0d ...
Debido a las limitaciones de potencia de procesamiento, el programa utiliza un modelo probabilístico (mediante el uso de una generador de números aleatorios o RNG) en lugar de en realidad la generación de texto al azar y comparándolo con Shakespeare. Cuando el simulador "detecta una coincidencia" (es decir, el generador de números aleatorios genera un cierto valor o un valor dentro de un cierto rango), el simulador simula el partido mediante la generación de texto coincidente.
Preguntas sobre las estadísticas que describen la frecuencia con un mono ideal debe escribir ciertas cadenas puedan motivar pruebas prácticas para los generadores de números aleatorios, así; Estos van desde lo simple a lo "bastante sofisticado". Profesores de informática George Marsaglia y Arif Zaman informan que utilizan para llamar a tales pruebas "m- superposición pruebas de tupla "en conferencia, puesto que se refieren m-tuplas de elementos sucesivos superpuestos en una secuencia aleatoria. Pero se encontraron con que los llaman" pruebas de mono "ayudaron a motivar a la idea con los estudiantes. Ellos publicaron un informe sobre la clase de pruebas y de su resultados para varios generadores de números aleatorios en 1993.
Monos reales
Conductistas Primate Cheney y Seyfarth observación de que los monos reales podrían de hecho tener que depender de la oportunidad de tener alguna esperanza de producir Romeo y Julieta . A diferencia de los simios , y en particular los chimpancés , la evidencia sugiere que los monos carecen de un teoría de la mente y no son capaces de diferenciar entre su propio y el conocimiento de los demás, las emociones y creencias. Incluso si un mono podría aprender a escribir una obra de teatro y describir los personajes comportamiento, no podía revelar los personajes mentes y así construir una tragedia irónica.
En 2003, profesores y estudiantes de la Universidad de Plymouth curso MediaLab Artes utiliza una subvención £ 2000 de la Consejo de las Artes para estudiar la producción literaria de los monos reales. Dejaron un teclado de computadora en el recinto de seis Célebes Crested Macacos en Paignton Zoo en Devon en Inglaterra durante un mes, con un enlace de radio para transmitir los resultados en una página web. Un investigador, Mike Phillips, defendió el gasto por ser más baratos que los reality shows y todavía "muy estimulante y fascinante visión".
No sólo los monos producen nada más que cinco páginas que consisten en gran parte de la carta S, la principal masculino comenzó golpeando el teclado con una piedra, y los monos continuó por orinar y defecar en ella. Responsable científico del zoológico remarcado que el experimento había "poco valor científico, excepto para mostrar que la teoría del" mono infinito 'es defectuoso ". Phillips dijo que el proyecto financiado por el artista era sobre todo el arte del performance, y que había aprendido "muchísimo" de ella. Llegó a la conclusión de que los monos "no son generadores aleatorios. Son más complejo que eso. ... Eran muy interesados en la pantalla, y vieron que cuando escriben una carta, algo pasó. Había un nivel de intención de allí."
Cultura popular
El teorema del mono infinito y su imaginería asociada se considera una muy popular y ilustración proverbial de las matemáticas de la probabilidad, ampliamente conocido por el público en general debido a su transmisión a través de la cultura popular en vez de por su transmisión a través de la sala de clases.
La naturaleza duradera, extendida y popular del conocimiento del teorema se señaló en la introducción de un documento de 2001, "Los monos, Máquinas de escribir y Redes - Internet en la luz de la Teoría de la Accidental Excelencia" (Hoffmann y Hofmann). En 2002, un Artículo del Washington Post dijo: "Un montón de gente ha tenido la diversión con la famosa idea de que un número infinito de monos con un número infinito de máquinas de escribir y una cantidad infinita de tiempo podría llegar a escribir las obras de Shakespeare." En 2003, los ya mencionados Consejo de las Artes experimento financiado la participación de monos reales y un teclado de computadora recibió amplia cobertura de prensa. En 2007, el teorema fue catalogado por La revista Wired en una lista de ocho clásico pensado experimentos.
La historia de las imágenes de 'monos escribiendo' se remonta por lo menos en cuanto a uso de Borel de la metáfora en su ensayo de 1913, y estas imágenes se ha repetido muchas veces desde entonces en una variedad de medios de comunicación. Hoy en día, el interés popular en los monos de mecanografía es sostenida por numerosas apariciones en la literatura, la televisión y la radio, música e Internet, así como novelas gráficas y stand-up rutinas de comedia.