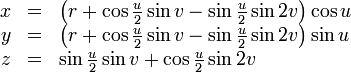Botella de Klein
Antecedentes
SOS ofrecen una descarga completa de esta selección de escuelas para su uso en escuelas intranets. Todos los niños disponibles para el apadrinamiento de niños de Aldeas Infantiles SOS son atendidos en una casa de familia por la caridad. Leer más ...

En matemáticas , la botella de Klein es cierto no orientable superficie, es decir, una superficie (una de dos dimensiones espacio topológico) sin y lados distintos "interiores", "exteriores". Otros objetos que no son orientables relacionados incluyen la Cinta de Moebius y la plano proyectivo real. Considerando que una tira de Möbius es un objeto de dos dimensiones con un lado y un borde, una botella Klein es un objeto tridimensional con un lado y sin bordes. (Para comparación, una esfera es un objeto tridimensional sin bordes y dos lados).
La botella de Klein fue descrita por primera vez en 1882 por el alemán matemático Felix Klein. Originalmente fue nombrado la "superficie Klein" Kleinsche Fläche; sin embargo, esto fue interpretado incorrectamente como Kleinsche Flasche "botella de Klein", que en última instancia condujo a la adopción de este término en el idioma alemán.
Construcción
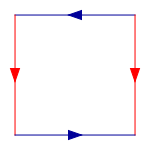
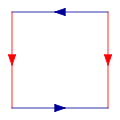
Comience con un cuadrado, y luego pegar juntos correspondientes bordes de colores, en el siguiente diagrama, de modo que las flechas partido. Más formalmente, la botella de Klein es el espacio cociente descrito como el cuadrado [0,1] × [0,1] con lados identificados por las relaciones (0, y) ~ (1, y) para 0 ≤ y ≤ 1 y (x, 0) ~ (1 - x, 1) para 0 ≤ x ≤ 1:
Esta plaza es un polígono fundamental de la botella Klein.
Tenga en cuenta que este es un "abstracto" pegado en el sentido de que tratar de darse cuenta de esto en tres dimensiones los resultados en una botella de Klein autointerseca. La botella de Klein, correcta, ¿no auto-intersecan. Sin embargo, hay una manera de visualizar la botella Klein como está contenida en cuatro dimensiones.
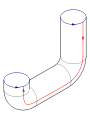
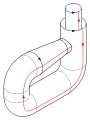
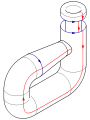
Pegue las flechas rojas de la plaza juntos (lados izquierdo y derecho), lo que resulta en un cilindro. Para pegar los extremos juntos de modo que las flechas en el partido círculos, pasan a través de un extremo del lado del cilindro. Tenga en cuenta que esto crea un círculo de auto-intersección. Esto es un inmersión de la botella de Klein en tres dimensiones.
Mediante la adición de un cuarto a la dimensión espacio tridimensional, la auto-intersección puede ser eliminada. Poco a poco empujar un trozo de tubo que contiene la intersección de las tres dimensiones del espacio inicial. Una analogía útil es considerar una curva autointerseca en el avión; auto-intersecciones pueden ser eliminados mediante el levantamiento de una hebra del avión.
Esta inmersión es útil para visualizar muchas propiedades de la botella de Klein. Por ejemplo, la botella de Klein no tiene límite, donde la superficie se detiene bruscamente, y es no orientable, como se refleja en la unilateralidad de la inmersión.

El modelo físico común de una botella Klein es una construcción similar. La Museo de la Ciencia Británica tiene en exhibición una colección de botellas de Klein de vidrio soplado a mano, exhibiendo muchas variaciones sobre este tema topológico. Las botellas datan de 1995 y fueron hechos para el museo por Alan Bennett. Clifford Stoll, autor de Huevo del cuco, fabrica botellas de Klein y los vende a través de Internet en Botella Acme Klein.
Propiedades
La botella de Klein puede ser visto como una haz de fibras como sigue: se toma la plaza desde arriba para ser E, el espacio total, mientras que el espacio de base B está dada por la unidad de intervalo en x, y la proyección π está dada por π (x, y) = x. Dado que se identifican los dos extremos del intervalo unidad en x, el espacio de base B es en realidad el círculo S 1, y así la botella Klein es el trenzado S 1 -bundle ( haz de círculo) sobre el círculo.
Como el Cinta de Moebius, la botella de Klein es una diferenciable bidimensional colector que no es orientable. A diferencia de la cinta de Moebius, la botella de Klein es una variedad cerrada, lo que significa que es un compacto colector sin límite. Mientras que la cinta de Moebius se puede incrustar en tres dimensiones del espacio euclidiano R 3, la botella de Klein no puede. Se puede incrustar en R 4, sin embargo.
La botella de Klein puede ser construido (en un sentido matemático, porque no se puede hacer sin permitir que la superficie a cortar a sí mismo) uniendo los bordes de dos bandas de Möbius juntos, como se describe en el siguiente anónimo quintilla :
- Un matemático llamado Klein
- Pensamos que la banda de Möbius era divino.
- Él dijo: "Si pegar
- Los bordes de dos,
- Usted obtendrá una botella raro como el mío ".
También se puede construir doblando una tira de Möbius por la mitad longitudinalmente y uniendo el borde a sí mismo.
Seis colores bastan para colorear cualquier mapa en la superficie de una botella Klein; esta es la única excepción a la Conjetura Heawood, una generalización del teorema de los cuatro colores , lo que requeriría siete.
Una botella de Klein es equivalente a una esfera más dos tapas cruzadas.
Disección

La disección de una botella Klein en dos mitades a lo largo de su plano de simetría resulta dos imagen espejo en Bandas de Möbius, es decir, uno de ellos con una media vuelta de tuerca con la mano izquierda y el otro con una media vuelta de tuerca con la mano derecha (una de ellas es la foto de la derecha). Recuerde que la intersección en la foto no está realmente allí. De hecho, también es posible cortar la botella Klein en una sola cinta de Möbius.
Parametrización

La "figura 8" inmersión de la botella de Klein tiene una particularmente simple parametrización:
En esta inmersión, el círculo de auto-intersección geométrica es un círculo en el plano xy. La constante positiva r es el radio de este círculo. El parámetro u da el ángulo en el plano xy, y v especifica la posición alrededor de la sección transversal en forma de 8.
La parametrización de la inmersión de 3 dimensiones de la botella en sí es mucho más complicado. Aquí está una versión simplificada:
donde
para 0 ≤ u <2π y 0 ≤ v <2π.
En esta parametrización, u sigue la longitud del cuerpo de la botella mientras v va alrededor de su circunferencia.
Las generalizaciones
La generalización de la botella de Klein a mayor género se da en el artículo sobre el polígono fundamental.
Superficie de Klein
Una superficie de Klein es, como para las superficies de Riemann , una superficie con un atlas que permite que la funciones de transición se pueden componer con conjugación compleja puede obtiene el llamado estructura dianalytic.