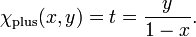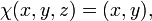Colector

En una esfera, la suma de los ángulos de un triángulo no es igual a 180 ° (ver trigonometría esférica). Una esfera no es un espacio euclidiano, pero localmente las leyes de la geometría euclidiana son buenas aproximaciones. En un pequeño triángulo en la faz de la tierra, la suma de los ángulos es casi 180 °. Una esfera puede ser representado por una colección de dos mapas dimensionales, por lo tanto, una esfera es un colector.

Un colector es un resumen espacio matemático en el que cada punto tiene una barrio que se asemeja espacio euclidiano , pero en el que la estructura global puede ser más complicado. En los múltiples discusiones, la idea de dimensión es importante. Por ejemplo, las líneas son unidimensionales, y planos de dos dimensiones.

En un colector unidimensional (o de un colector), cada punto tiene un vecindario que se parece a un segmento de una línea. Ejemplos de uno-variedades incluyen una línea, un círculo , y dos círculos separados. En un dos-variedad, cada punto tiene un barrio que parece un disco. Los ejemplos incluyen un plano, la superficie de una esfera , y la superficie de un toro .

Los colectores son objetos importantes de las matemáticas y la física , ya que permiten estructuras más complicadas para expresarse y entenderse en términos de las propiedades relativamente bien entendidos de los espacios más simples.

Estructuras adicionales a menudo se definen en variedades. Ejemplos de colectores con una estructura adicional incluyen variedades diferenciables en el que uno puede hacer el cálculo , Variedades de Riemann en la que las distancias y los ángulos se pueden definir, simplécticos colectores que sirven de espacio de fase en la mecánica clásica y la de cuatro dimensiones colectores pseudo-riemanniana que modelan espacio-tiempo en la relatividad general .

Una definición matemática precisa de un colector es la siguiente. Para entender completamente las matemáticas detrás de los colectores, es necesario conocer los conceptos elementales relativas a los conjuntos y funciones , y útil tener un conocimiento práctico de cálculo y topología .

Ejemplos de motivación

Círculo

Figura 1: El cuatro cartas cada mapa parte del círculo de un intervalo abierto, y juntos cubren todo el círculo.

El círculo es el ejemplo más simple de una variedad topológica después de una línea. Topología ignora flexión, por lo que una pequeña pieza de un círculo es exactamente lo mismo que un pequeño trozo de una línea. Consideremos, por ejemplo, la mitad superior de la círculo unidad, x ² + y ² = 1, en donde la coordenada y es positivo (indicado por el arco amarillo en la Figura 1). Cualquier punto de este semicírculo puede ser descrito de forma única por su coordenada x. Por lo tanto, proyección sobre la primera coordenada es un continua, y invertible , mapeo desde el semicírculo superior a la intervalo abierto (-1,1):

Tales funciones se llaman carta s. Del mismo modo, hay cartas para el (verde) piezas correctas del círculo inferior (rojo), izquierda (azul), y. En conjunto, estas piezas cubren todo el círculo y las cuatro cartas forman un atlas para el círculo.

Los gráficos superior y derecho se superponen: su intersección se encuentra en la cuarta parte del círculo donde tanto el x - y las coordenadas x y son positivos. La _{parte superior} dos gráficos χ y χ _derecho cada mapa esta parte en el intervalo (0,1). Por lo tanto una función de T (0,1) a sí mismo se puede construir, que primero utiliza la inversa de la tabla de la parte superior para alcanzar el círculo y luego sigue el gráfico de la derecha de nuevo a la intervalo. Sea a cualquier número en (0,1), entonces:

Tal función se denomina un mapa de transición.

Figura 2: Un círculo gráfico múltiple basado en pendiente, que cubre todo menos un punto de la circunferencia.

La parte superior, inferior, izquierda y derecha gráficos muestran que el círculo es una variedad, pero que no forman el único atlas posibles. Gráficas no necesitan ser proyecciones geométricas, y el número de cartas es una cuestión de cierta elección. Considere las listas

y

Aquí S es la pendiente de la recta que pasa por el punto en las coordenadas (x, y) y el punto de pivote fijo (-1,0); t es la imagen especular, con punto de giro (+1,0). La aplicación inversa de s a (x, y) viene dada por

Puede ser fácilmente confirmó que x ² + y ² = 1 para todos los valores de la pendiente s. Estos dos cuadros ofrecen un segundo atlas para el círculo, con

Cada gráfico omite un solo punto, ya sea (-1,0) para s o (+1,0) para t, por lo que ni la carta por sí sola es suficiente para cubrir todo el círculo. Topología puede demostrar que no es posible cubrir el círculo completo con una sola carta. Por ejemplo, aunque es posible construir un círculo de un solo intervalo de línea mediante la superposición y "encolar" los extremos, esto no produce un gráfico; una porción del círculo se asignará a ambos extremos a la vez, perdiendo invertibilidad.

Otras curvas

Cuatro variedades de curvas algebraicas: ■ círculos, ■ parábola, hipérbola ■, ■ cúbico.

Los colectores no tienen que ser conectado (todo en "una sola pieza"); por lo tanto un par de círculos separados es también un colector. No necesitan ser cerrada; por lo tanto un segmento de línea sin sus puntos finales es un colector. Y ellos no tienen por qué ser finito; así una parábola es un colector. Poner estas libertades juntos, otros dos ejemplos de colectores son una hipérbola (dos piezas, infinitas abiertas) y la locus de puntos de la curva y cúbico ² = x ³ - x (un pedazo de circuito cerrado y una pieza infinito abierto).

Sin embargo, se excluyen los ejemplos como dos círculos conmovedoras que comparten un punto para formar una figura-8; en el punto compartido no podemos crear un gráfico satisfactoria. Incluso con la flexión permitido por la topología, la proximidad del punto compartido se parece a un "+", no una línea.

Círculo Enriquecido

Visto utilizando el cálculo , la función de circunferencia de transición T es simplemente una función entre intervalos abiertos, lo que da sentido a la afirmación de que T es diferenciable . El mapa de transición T, y todos los otros, son diferenciable en (0, 1); por lo tanto, con este Atlas El círculo es una variedad diferenciable. Es también suave y analítica porque las funciones de transición tienen estas propiedades también.

Otras propiedades del círculo le permiten satisfacer las necesidades de los tipos más especializados de colector. Por ejemplo, el círculo tiene una noción de distancia entre dos puntos, la longitud del arco entre los puntos; por lo tanto es una Variedad de Riemann.

Historia

El estudio de las variedades combina muchas áreas importantes de las matemáticas: se generaliza conceptos tales como curvas y superficies, así como ideas de álgebra lineal y topología .

Prehistoria

Antes de que el concepto moderno de un colector hubo varios resultados importantes.

La geometría no-euclidiana considera espacios donde Euclides 's postulado de las paralelas falla. Saccheri los estudió por primera vez en 1733. Lobachevsky, Bolyai y Riemann los desarrolló 100 años más tarde. Su investigación reveló dos tipos de espacios cuyas estructuras geométricas diferir de la de clásica espacio euclidiano ; éstos dieron lugar a geometría hiperbólica y geometría elíptica. En la moderna teoría de colectores, estas nociones corresponden a Variedades de Riemann con constante negativa y positiva curvatura, respectivamente.

Carl Friedrich Gauss puede haber sido el primero en considerar espacios abstractos como objetos matemáticos en su propio derecho. Su Egregium theorema da un método para calcular la curvatura de una superficie sin tener en cuenta la espacio ambiente en el que la superficie se encuentra. Tal superficie sería, en terminología moderna, ser llamado un colector; y en términos modernos, el teorema demuestra que la curvatura de la superficie es una propiedad intrínseca. Teoría del colector ha llegado a centrarse exclusivamente en estas propiedades intrínsecas (o invariantes), sin tener en cuenta en gran medida las propiedades extrínsecas del espacio ambiente.

Otra, más topológica ejemplo de una intrínseca propiedad de un colector es su característica de Euler . Leonhard Euler demostró que para una convexa politopo en el espacio euclidiano tridimensional con vértices V (o esquinas), los extremos E, F y caras,

V - E + F = 2.

La misma fórmula celebrará si proyectamos los vértices y aristas del politopo sobre una esfera , creando un "mapa" con los vértices V, bordes E y F se enfrenta, y de hecho, seguirá siendo cierto para cualquier mapa esférica, aunque no se deriva de ninguna politopo convexo. Por lo tanto 2 es una invariante topológico de la esfera, denominado su característica de Euler. Por otro lado, un toro puede ser cortado abierto por su círculos meridianos '' paralelo 'y, la creación de un mapa con V = 1 vértice, E = 2 bordes, y F = 1 cara. Así, la característica de Euler del toro es 1.2 + 1 = 0. La característica de Euler de otras superficies es un útil invariante topológico, que puede ampliarse a dimensiones superiores utilizando Números de Betti. A mediados del siglo XIX, el Teorema de Gauss-Bonnet vinculó la característica de Euler a la curvatura de Gauss.

Síntesis

Las investigaciones de Niels Henrik Abel y Carl Gustav Jacobi sobre inversión de integrales elípticas en la primera mitad del siglo 19 les llevó a considerar un tipo especial de variedades complejas, ahora conocido como Jacobianos. Bernhard Riemann contribuyó aún más a su teoría, aclarando el significado geométrico del proceso de continuación analítica de funciones de variables complejas, aunque estas ideas estaban muy por delante de su tiempo.

Otra fuente importante de colectores en las matemáticas del siglo 19 fue mecánica analítica, desarrollados por Simeón Poisson, Jacobi, y William Rowan Hamilton. Los posibles estados de un sistema mecánico se cree que son puntos de un espacio abstracto, espacio de fase en Lagrange y Formalismos hamiltoniana de la mecánica clásica. Este espacio es, de hecho, un colector de alta dimensión, cuyo dimensión corresponde a los grados de libertad del sistema y donde los puntos se especifican por su coordenadas generalizadas. Para un movimiento sin restricciones de partículas libres del colector es equivalente al espacio euclidiano, pero vario leyes de conservación limitan a formaciones más complejas, por ejemplo, Liouville tori. La teoría de un cuerpo sólido en rotación, desarrollado en el siglo 18 por Leonhard Euler y Joseph Lagrange , da otro ejemplo en el que el colector no es trivial. Aspectos geométricos y topológicos de la mecánica clásica se destacaron por Henri Poincaré, uno de los fundadores de la topología .

Riemann fue el primero en hacer una amplia labor generalizando la idea de una superficie de dimensiones superiores. El colector nombre proviene de originales de Riemann alemán plazo, Mannigfaltigkeit, que William Kingdon Clifford traduce como "multiplicidad". En su conferencia inaugural Göttingen, Riemann se describe el conjunto de todos los valores posibles de una variable con ciertas limitaciones como Mannigfaltigkeit, ya que la variable puede tener muchos valores. Distingue entre stetige Mannigfaltigkeit y diskrete Mannigfaltigkeit (multiplicidad continua y multiplicidad discontinua), dependiendo de si los cambios de valor de forma continua o no. Como ejemplos continuos, Riemann se refiere no sólo a los colores y las ubicaciones de los objetos en el espacio, sino también las posibles formas de una figura espacial. Uso inducción, Riemann construye un n-fach ausgedehnte Mannigfaltigkeit (n veces multiplicidad extendida o multiplicidad n-dimensional) como una pila continua de (n-1) manifoldnesses dimensionales. Noción intuitiva de Riemann de una Mannigfaltigkeit se convirtió en lo que hoy es formalizado como un colector. Variedades de Riemann y superficies de Riemann llevan el nombre de Bernhard Riemann.

Hermann Weyl dio una definición intrínseca de variedades diferenciables en su curso de conferencias sobre superficies de Riemann en 1911-1912, abriendo el camino para el concepto general de un espacio topológico que siguió en breve. Durante la década de 1930 Hassler Whitney y otros aclararon la aspectos fundamentales de la materia, y por lo tanto las intuiciones que se remontan a la segunda mitad del siglo 19 se convirtió precisa, y se desarrollan a través de la geometría diferencial y La teoría de grupos de Lie.

Topología de variedades: destacados

Colectores de dos dimensiones, también conocidas como las superficies, fueron considerados por Riemann bajo la apariencia de las superficies de Riemann , y rigurosamente clasificado en el comienzo del siglo 20 por Poul Heegaard y Max Dehn. Henri Poincaré fue pionero en el estudio de las variedades tridimensionales y planteó una pregunta fundamental acerca de ellos, hoy conocido como el Conjetura de Poincaré. Después de casi un siglo de esfuerzos por muchos matemáticos, empezando por el propio Poincaré, un consenso entre los expertos (a partir de 2006) es que Grigori Perelman ha demostrado la conjetura de Poincaré (véase el Solución de la conjetura de Poincaré Hamilton-Perelman). Bill Thurston programa de geometrización, formulada en la década de 1970, a condición de una extensión de largo alcance de la conjetura de Poincaré a las variedades tridimensionales generales. Cuatro dimensiones colectores fueron llevados a la vanguardia de la investigación matemática en la década de 1980 por Michael Freedman y en un entorno diferente, por Simon Donaldson, que fue motivado por el entonces reciente progreso en la física teórica ( Yang-Mills teoría), donde sirven como sustituto del ordinario "plana" espacio tiempo. Un trabajo importante en variedades de dimensiones superiores, incluyendo los análogos de la conjetura de Poincaré, se había hecho antes por René Thom, John Milnor, Stephen Smale y Sergei Novikov. Una de las técnicas más extendidas y flexibles subyacentes mucho trabajo en la topología de variedades es La teoría de Morse.

Definición matemática

Informalmente, un colector es una espacio que está "inspirado en" el espacio euclidiano .

Hay muchos tipos diferentes de colectores y generalizaciones. En la geometría y la topología, todas las variedades son variedades topológicas, posiblemente con una estructura adicional, lo más a menudo una estructura diferenciable. En cuanto a la construcción de colectores a través de parches, un colector tiene una estructura adicional si los mapas de transición entre los diferentes parches satisfacen los axiomas más allá de la continuidad. Por ejemplo, variedades diferenciables tienen homeomorfismos en barrios superpuestas difeomorfa uno con el otro, de modo que el colector tiene un conjunto bien definido de funciones que son diferenciables en cada barrio, y así diferenciable en el colector en su conjunto.

Formalmente, un colector topológico es una segundo contable Hausdorff espacio que es localmente homeomorfo al espacio euclidiano.

Segundo contable y Hausdorff son condiciones de punto de ajuste; segundo excluye contables espacios de mayor cardinalidad como el línea larga, mientras Hausdorff excluye espacios como "la línea con dos orígenes" (estos colectores generales se discuten en no Hausdorff colectores).

Localmente homeomorfo al espacio euclidiano significa que cada punto tiene un vecindario homeomorfo a un abierto euclidiano n -rodamientos,

Generalmente se toman colectores tener una dimensión fija (el espacio debe ser localmente homeomorfo a un fijo n -rodamientos), y un espacio de este tipo se denominan n -manifold; Sin embargo, algunos autores admitir colectores en diferentes puntos pueden tener diferente dimensiones. Desde dimensión es una invariante local, cada componente conectado tiene una dimensión fija.

Esquema teóricamente, un colector es una anillado localmente espacio, cuya estructura gavilla es localmente isomorfo a la gavilla de continua (o diferenciable, o complejo-analítica, etc.) funciones en el espacio euclidiano. Esta definición se utiliza sobre todo cuando se habla de colectores analíticos en geometría algebraica.

Definición amplia

La definición común más amplio de colector es un espacio topológico localmente homeomorfo a un espacio vectorial topológico sobre los reales. Esto omite los axiomas de punto-set (permitiendo cardinalidades mayores y no Hausdorff colectores) y la dimensión finita (que permite varios colectores de análisis funcional). Por lo general, uno se relaja una u otra condición: colectores sin los axiomas-set point se estudian en topología general, mientras que las variedades de dimensión infinita se estudian en análisis funcional.

Cuadros, atlas y mapas de transición

La Tierra esférica se navega utilizando mapas o cartas planas, recogidos en un atlas. Del mismo modo, una variedad diferenciable puede ser descrito usando mapas matemáticos, llamados coordinar gráficos, recogidos en un atlas matemáticos. Generalmente no es posible describir un colector con una sola tabla, debido a que la estructura global del colector es diferente de la estructura simple de los gráficos. Por ejemplo, ningún mapa plano puede representar adecuadamente a toda la Tierra. Cuando un colector se construye a partir de varios gráficos superpuestos, las regiones donde se superponen llevan la información esencial para la comprensión de la estructura global.

Gráficas

Un mapa de coordenadas, un gráfico de coordenadas, o simplemente un gráfico, de un colector es un invertible mapa entre un subconjunto del colector y un espacio sencillo de tal manera que tanto el mapa y su inversa preservar la estructura deseada. Para una variedad topológica, el espacio simple es cierto espacio euclidiano R ⁿ y el interés se centra en la estructura topológica. Esta estructura se conserva por homeomorfismos , mapas invertibles que son continuos en ambas direcciones.

En el caso de una variedad diferenciable, un juego de cartas llamado un atlas nos permite hacer el cálculo en variedades. Las coordenadas polares , por ejemplo, de un gráfico para el plano ^R2 menos el eje x positivo y el origen. Otro ejemplo de un gráfico es el _alto Mapa χ mencionado en el apartado anterior, un gráfico para el círculo.

Atlas

La descripción de la mayoría de los colectores requiere más de un gráfico (una sola tabla es adecuada sólo para los colectores más simples). Una colección específica de las cartas que cubre un colector se llama un atlas. Un atlas no es única ya que todos los colectores se pueden cubrir múltiples maneras utilizando diferentes combinaciones de cartas.

El atlas contienen todas las cartas posibles compatibles con un determinado atlas se llama el atlas máximos. A diferencia de un atlas ordinarias, el atlas máximas de un colector dado es único. Aunque es útil para definiciones, es un objeto muy abstracta y no se utiliza directamente (por ejemplo, en los cálculos).

Mapas de transición

Gráficos en un atlas pueden superponerse y un único punto de un colector pueden ser representados en varios gráficos. Si dos gráficos se superponen, partes de ellos representan la misma región del colector, así como un mapa de Europa y un mapa de Asia pueden contener tanto Moscú. Dadas dos tablas superpuestas, una función de transición se pueden definir que va de una bola abierta en R ⁿ al colector y luego de vuelta a otro (o quizás el mismo) bola abierta en R ^n. El mapa resultante, como el mapa de T en el ejemplo del círculo anterior, se llama un cambio de coordenadas, una transformación de coordenadas, una función de transición, o un mapa de transición.

Estructura adicional

Un atlas también se puede utilizar para definir una estructura adicional en el colector. La estructura se define por primera vez en cada tabla por separado. Si todos los mapas de transición son compatibles con esta estructura, la estructura de las transferencias al colector.

Esta es la manera estándar de variedades diferenciables se definen. Si las funciones de transición de un atlas para un colector topológico preservar la estructura diferencial natural de R ⁿ (es decir, si están difeomorfismos), la estructura diferencial de las transferencias a el colector y la convierte en una variedad diferenciable. Variedades complejas se introducen de una manera análoga al requerir que las funciones de transición de un atlas son funciones holomorfas. Para colectores simplécticos, las funciones de transición deben ser simplectomorfismos.

La estructura en el colector depende de los atlas, pero a veces diferentes atlas puede decir para dar lugar a la misma estructura. Tales atlas se llaman compatible.

Estas nociones se hacen precisa en general mediante el uso de pseudogroups.

Construcción

Un solo colector puede construirse de diferentes maneras, cada destacando un aspecto diferente del colector, lo que conduce a un punto de vista ligeramente diferente.

Gráficas

El gráfico de los mapas de la parte de la esfera con z positiva de coordenadas en un disco.

Tal vez la forma más sencilla de construir un colector es el utilizado en el ejemplo anterior del círculo. En primer lugar, un subconjunto de R ² se identifica, y luego se construye un atlas que abarca este subconjunto. El concepto de colector creció históricamente de construcciones como esta. He aquí otro ejemplo, la aplicación de este método para la construcción de una esfera:

Esfera con las cartas

Una esfera se puede tratar casi de la misma manera que el círculo. En matemáticas una esfera es sólo la superficie (no el interior sólido), que se puede definir como un subconjunto de R ^3:

La esfera es de dos dimensiones, por lo que cada cuadro le asignar parte de la esfera de un abierto de R ^2. Considere el hemisferio norte, que es la parte con z positivo de coordenadas (de color rojo en la imagen a la derecha). El χ función definida por

mapas del hemisferio norte a la intemperie disco de la unidad mediante la proyección sobre la (x, y) avión. Existe una tabla similar para el hemisferio sur. Junto con dos cartas que se proyectan en el (x, z) avión y dos cartas que se proyectan en el plano (y, z), se obtiene un atlas de seis cartas que cubre toda la esfera.

Esto se puede generalizar fácilmente a las esferas de dimensiones superiores.

Patchwork

Un colector puede construirse pegando piezas de una manera coherente, por lo que en gráficos superpuestos. Esta construcción es posible para cualquier colector y de ahí que se utiliza a menudo como una caracterización, especialmente para las variedades diferenciables y Riemann. Se centra en un atlas, como los parches proporcionan, naturalmente, gráficos, y puesto que no hay espacio exterior involucrados conduce a una vista intrínseca del colector.

El colector se construye mediante la especificación de un atlas, que se define por sí misma mapas de transición. Por lo tanto, un punto A del colector es clase de equivalencia de puntos que se asigna a sí por mapas de transición. Gráficos mapa clases de equivalencia de puntos de un solo parche. Por lo general hay fuertes demandas sobre la consistencia de los mapas de transición. Por variedades topológicas están obligados a ser homeomorfismos ; si también son difeomorfismos, el colector resultante es una variedad diferenciable.

Esto se puede ilustrar con el mapa de transición t = ¹ / _s de la segunda mitad del ejemplo de círculo. Comience con dos copias de la línea. Utilice la s de coordenadas para la primera copia, y t para la segunda copia. Ahora, pegar las dos copias junto al identificar el punto t en la segunda copia con el punto ¹ / _s de la primera copia (el punto t = 0 no se identifica con cualquier punto de la primera copia). Esto da un círculo.

Vista intrínseca y extrínseca

La primera construcción y esta construcción son muy similares, pero representan bastante diferentes puntos de vista. En la primera construcción, el colector se ve como incrustado en algún espacio euclidiano. Esta es la opinión extrínseca. Cuando un colector se ve de esta manera, es fácil de usar la intuición de los espacios euclidianos para definir una estructura adicional. Por ejemplo, en un espacio euclídeo siempre está claro si un vector en algún momento es tangencial o normal a alguna superficie a través de ese punto.

La construcción de retazos no utiliza ningún tipo de incorporación, sino que simplemente ve el colector como un espacio topológico por sí mismo. Este punto de vista abstracto se llama el punto de vista intrínseco. Se puede hacer que sea más difícil de imaginar lo que podría ser un vector tangente.

n -Sphere como un mosaico

La n -sphere S ⁿ es una generalización de la idea de un círculo (1-esfera) y la esfera (2-esfera) de dimensiones superiores. Un -sphere n S ⁿ puede ser construido pegando dos copias de R ^n. El mapa de transición entre ellos se define como

Esta función es su propia inversa y por lo tanto se puede utilizar en ambas direcciones. Como el mapa de transición es una función suave, este atlas define un colector suave. En el caso n = 1, el ejemplo simplifica al ejemplo círculo dado antes.

La identificación de los puntos de un colector

Es posible definir diferentes puntos de un colector a ser el mismo. Esto puede ser visualizado como encolado estos puntos juntos en un único punto, formando una espacio cociente. Hay, sin embargo, no hay razón para esperar que tales espacios cocientes sean colectores. Entre los posibles espacios cocientes que no son necesariamente los colectores, orbifolds y Complejos de CW se consideran relativamente de buen comportamiento.

Un método para la identificación de puntos (pegándolas juntas) es a través de una derecha (o izquierda) acción de un grupo , el cual actúa sobre el colector. Dos puntos son identificados si uno se mueve en el otro por un elemento de grupo. Si M es el colector y G es el grupo, el espacio cociente resultante se denota por M / G (o G \ M).

Colectores que pueden construirse mediante la identificación de puntos incluyen tori y espacios proyectivos reales (comenzando con un plano y una esfera, respectivamente).

Productos cartesianos

La Producto cartesiano de colectores es también un colector. No todos colector se puede escribir como un producto de otros colectores.

La dimensión del colector de producto es la suma de las dimensiones de sus factores. Su topología es la topología del producto, y un producto cartesiano de gráficos es un gráfico para el colector de producto. Por lo tanto, un atlas para el colector de producto se puede construir usando atlas por sus factores. Si estos atlas definen una estructura diferencial de los factores, el atlas correspondientes define una estructura diferencial en el múltiple de producto. Lo mismo es cierto para cualquier otra estructura definida en los factores. Si uno de los factores tiene un límite, el colector de producto, también tiene un límite. Productos cartesianos pueden ser usados para construir Tori y finito cilindros, por ejemplo, como S ¹ × S ¹ y S ¹ × [0, 1], respectivamente.

Un cilindro finito es una variedad con borde.

Variedad con borde

Una variedad con borde es un colector con un borde. Por ejemplo, una hoja de papel con esquinas redondeadas es una 2-variedad con un límite de 1-dimensional. El borde de un -manifold n es un (n -1) -manifold. La disco (círculo más interior) es un 2-variedad con borde. Su límite es un círculo, un 1-variedad . La bola (esfera más interior) es una 3-variedad con borde. Su límite es una esfera, un 2-variedad. (Ver también Límites (topología)).

En lenguaje técnico, una variedad con frontera es un espacio que contiene los dos puntos interiores y puntos de frontera. Cada punto interior tiene un homeomorfo barrio al n -rodamientos abierto {(x _1, x _2, ..., x _n) | Σ x _i ² <1}. Cada punto tiene un límite homeomorfo barrio de la "media" n -rodamientos {(x _1, x _2, ..., x _n) | Σ x _i ² <1 y x ₁ ≥ 0}. El homeomorfismo debe enviar el punto límite de un punto con x ₁ = 0.

Pegado a lo largo de las fronteras

Dos colectores con límites pueden ser pegadas entre sí a lo largo de una frontera. Si esto se hace de la manera correcta, el resultado es también un colector. Del mismo modo, dos límites de un solo colector se pueden pegar juntos.

Formalmente, el encolado se define por una biyección entre los dos límites. Dos puntos se identifican cuando se mapean en sí. Para una variedad topológica esta biyección debe ser un homeomorfismo, de lo contrario el resultado no será un colector topológico. Del mismo modo para una variedad diferenciable que tiene que ser un difeomorfismo. Para otros colectores de otras estructuras deben ser preservados.

Un cilindro finito puede construirse como un colector comenzando con una tira [0, 1] × [0, 1] y pegado de un par de bordes opuestos sobre el límite por un difeomorfismo adecuado. La plano proyectivo puede obtenerse mediante encolado una esfera con un agujero en él a una Cinta de Moebius lo largo de sus respectivas fronteras circulares.

Clases de colectores

Variedades topológicas

El tipo más simple de colector de definir es la variedad topológica, que se ve a nivel local como una "corriente" espacio euclidiano R ^n. Formalmente, un colector topológico es una espacio topológico localmente homeomorfo a un espacio euclidiano. Esto significa que cada punto tiene un barrio para los que existe un homeomorfismo (un biyectiva función continua cuya inversa también es continua) mapear ese barrio a R ^n. Estos homeomorfismos son las cartas del colector.

Es de señalar que una variedad topológica ve localmente como un espacio euclidiano de una manera más bien débil: mientras que para cada carta individual es posible distinguir funciones diferenciables o medir distancias y ángulos, por el mero hecho de ser una variedad topológica de un espacio hace no tiene ninguna opción particular y coherente de tales conceptos. Con el fin de discutir tales propiedades de un colector, es necesario especificar con mayor detalle la estructura y considerar las variedades diferenciables y variedades de Riemann se analizan a continuación. En particular, una misma variedad topológica subyacente puede tener varias clases mutuamente incompatibles de funciones diferenciables y un número infinito de formas de especificar distancias y ángulos.

Por lo general, se hacen supuestos técnicos adicionales en el espacio topológico para excluir casos patológicos. Se acostumbra a requerir que el espacio sea Hausdorff y segundo contable.

La dimensión del colector en un cierto punto es la dimensión del espacio euclidiano que las listas en el mapa de puntos que a (número n en la definición). Todos los puntos en una colector conectado tienen la misma dimensión. Algunos autores requieren que todos los gráficos de un mapa variedad topológica a euclidiana espacios de misma dimensión. En ese caso, cada variedad topológica tiene un invariante topológico, su dimensión. Otros autores permiten las uniones disjuntas de variedades topológicas con diferentes dimensiones para ser llamados colectores.

Variedades diferenciables

Para la mayoría de las aplicaciones de un tipo especial de colector topológico, una variedad diferenciable, se utiliza. Si las cartas locales en un colector son compatibles, en cierto sentido, se puede definir direcciones, espacios tangentes y funciones diferenciables en esa multiplicidad. En particular, es posible utilizar el cálculo en una variedad diferenciable. Cada punto de una variedad diferenciable n-dimensional tiene una espacio tangente. Este es un espacio euclidiano n-dimensional que consta de la vectores tangentes de las curvas a través del punto.

Dos clases importantes de variedades diferenciables son múltiples lisos y analíticas. Para múltiples lisos los mapas de transición son liso, que es infinitamente diferenciable. Colectores analíticos son múltiples lisos con la condición adicional de que los mapas de transición son analítica (que puede expresarse como series de potencias, que son esencialmente los polinomios de grado infinito). La esfera se puede dar estructura analítica, al igual que las curvas y superficies más familiares.

La conjunto rectificable generaliza la idea de un suave por partes o curva rectificable a dimensiones superiores; Sin embargo, los conjuntos no son subsanables en colectores generales.

Variedades de Riemann

Para medir distancias y ángulos en los colectores, el colector debe ser de Riemann. Una variedad de Riemann es una variedad diferenciable en el que cada espacio tangente está equipado con una producto interno <⋅, ⋅> de manera que varía suavemente de un punto a otro. Dados dos vectores tangentes u y v, el producto interno <u, v> da un número real. La punto (o escalar) producto es un ejemplo típico de un producto interno. Esto permite definir varias nociones tales como longitud, ángulos , áreas (o volúmenes ), curvatura, gradientes de funciones y divergencia de campos vectoriales.

Todas las variedades diferenciables (de dimensión constante) se puede dar la estructura de una variedad de Riemann. El espacio euclidiano sí conlleva una estructura natural de la variedad de Riemann (los espacios tangentes se identifican de forma natural con el propio espacio euclidiano y llevan el producto escalar estándar del espacio).Muchas curvas y superficies conocidas, incluyendo, por ejemplo, todos losn-spheres, se especifican como subespacios de un espacio euclidiano y heredan una métrica de su incrustación en él.

Colectores Finsler

Un colector de Finsler permite la definición de la distancia, pero no de ángulo; se trata de una variedad analítica en el que cada espacio tangente está equipado con una norma, || · ||, de una manera que varía suavemente de punto a punto. Esta norma se puede extender a una métrica, que define la longitud de una curva; pero no puede en general ser usado para definir un producto interno.

Cualquier variedad de Riemann es una variedad Finsler.

Grupos de Lie

Grupos de Lie, llamado así porSophus Lie, son variedades diferenciables que llevan también la estructura de ungrupoque es tal que las operaciones de los grupos se definen por mapas lisos.

Un espacio de vector con la operación del grupo de la suma de vectores es un ejemplo de un grupo de Lie no compacto. Un ejemplo simple de un compacto grupo de Lie es el círculo: la operación del grupo es simplemente rotación. Este grupo, conocido como T (1), también se puede caracterizar como el grupo de números complejos de módulo 1 con la multiplicación como la operación del grupo. Otros ejemplos de grupos de Lie incluyen grupos especiales de matrices , que son todos los subgrupos del grupo lineal general, el grupo de n por n matrices con determinante distinto de cero. Si las entradas de la matriz son números reales , esto va a ser un n ² -dimensional colector desconectado. La grupos ortogonales, los grupos de simetría de la esfera y hiperesferas, son n ( n -1) / 2 colectores de dimensiones, donde n -1 es la dimensión de la esfera. Otros ejemplos se pueden encontrar en la tabla de grupos de Lie.

Otros tipos de colectores

• La colector complejo es un colector inspirado en C ⁿ con funciones de transición holomorfas sobre superposiciones gráfico. Estos colectores son los objetos básicos de estudio en geometría compleja. Un colector de un complejo-dimensional se llama una superficie de Riemann . Tenga en cuenta que un n colector complejo dimensional tiene dimensión 2 n como una verdadera variedad diferenciable.
• La CR colectores un colector de modelado en los límites de los dominios enC ⁿ.
• Colectores de dimensiones infinitas: para permitir infinitas dimensiones, se puede considerarcolectores de Banach que son localmente homeomorfo a Espacios de Banach.Del mismo modo, colectores Fréchet son localmente homeomorfo a Espacios de Fréchet.
• La variedad simpléctica es un tipo de colector que se utiliza para representar los espacios de fase en la mecánica clásica . Dotados como están de una forma-2 que define el corchete de Poisson. Un tipo estrechamente relacionado de colector es un colector de contacto.

Clasificación y invariantes

Diferentes nociones de colectores tienen diferentes nociones de clasificación y invariante; en esta sección nos centramos en colectores cerrados lisos.

La clasificación de los colectores cerrados lisos es bien entendida , en principio , salvo en dimensión 4: en las dimensiones bajas (2 y 3) es geométrica, a través del teorema de uniformización y la solución de Hamilton-Perelman de la conjetura de Poincaré, y en alta dimensión ( 5 y superiores) es algebraica, a través de la teoría de la cirugía. Esta es una clasificación, en principio: la cuestión general de si dos colectores lisas son difeomorfa es no computable en general. Además, los cálculos específicos siguen siendo difíciles, y hay muchas preguntas abiertas.

Superficies orientables se pueden visualizar y sus clases difeomorfismo enumeran, por género. Dados dos superficies orientables, se puede determinar si son difeomorfa calculando sus respectivos géneros y comparando: son difeomorfa si y sólo si los géneros son iguales, por lo que el género constituye un conjunto completo de invariantes.

Esto es mucho más difícil en dimensiones superiores: colectores de dimensiones superiores no pueden ser visualizados directamente (aunque la intuición visual es útil en la comprensión de ellos), ni se puede enumerar sus clases difeomorfismo, ni se puede, en general, determinar si dos descripciones diferentes de un colector de dimensiones superiores se refieren al mismo objeto.

Sin embargo, se puede determinar si dos colectores son diferentes si hay alguna característica intrínseca que los diferencia. Tales criterios se refieren comúnmente como invariantes , porque, mientras que pueden ser definidos en términos de alguna presentación (tales como el género en términos de una triangulación), que son los mismos en relación con todas las posibles descripciones de un colector especial: son invariantes bajo diferentes descripciones.

Ingenuamente, uno podría esperar para desarrollar un arsenal de criterios invariantes que definitivamente clasificar todos los colectores hasta el isomorfismo. Por desgracia, se sabe que para colectores de dimensión 4 y superior, no existe ningún programa que puede decidir si dos colectores son difeomorfa.

Colectores lisas tienenun rico conjunto de invariantes, viniendo detopología punto-set, clásico topología algebraica, y topología geométrica.Las invariantes más familiares, que son visibles para las superficies, sonorientabilidad (una invariante normales, también detectado porhomología) ygénero (una invariante homológica).

Smooth colectores cerrados no tienen invariantes locales (excepto dimensión), aunque colectores geométricas tienen invariantes locales, en particular la curvatura de una variedad de Riemann y la torsión de un colector equipado con una conexión afín. Esta distinción entre no invariantes locales e invariantes locales es una forma común para distinguir entre la geometría y la topología. Todos los invariantes de un colector cerrado suave son, pues, global.

Topología algebraica es una fuente de una serie de importantes propiedades invariantes globales. Algunos criterios clave incluyen el simplemente conexo propiedad y capacidad de orientación (véase más adelante). De hecho varias ramas de las matemáticas, como la homología y de homotopía teoría, y la teoría de clases características fueron fundadas con el fin de estudiar las propiedades invariantes de colectores.

Ejemplos de superficies

Orientabilidad

En dos dimensiones y superior, un criterio invariante simple pero importante es la cuestión de si un colector admite una orientación significativa. Considere una variedad topológica con las cartas de asignación a R ⁿ . Dada una base ordenada para R ⁿ , un gráfico hace que su pedazo del colector a sí mismo adquirir un sentido de orden, que en 3-dimensiones se puede ver, ya sea diestro o zurdo. La superposición de gráficos no están obligados a estar de acuerdo en el sentido de ordenación, lo que da una libertad importante colectores. Para algunas variedades, como la esfera, las cartas pueden ser elegidos de manera que las regiones superpuestas están de acuerdo en su "imparcialidad"; estos son orientables colectores. Para otros, esto es imposible. Esta última posibilidad es fácil pasar por alto, ya que cualquier superficie cerrada incrustado (sin auto-intersección) en el espacio tridimensional es orientable.

Algunos ejemplos ilustrativos de colectores no orientables incluyen: (1) lacinta de Möbius, que es una variedad con borde, (2) labotella de Klein, que debe cortarse consigo mismo en 3-espacio, y (3) elplano proyectivo real, que surge naturalmente enla geometría.

Cinta de Moebius

Cinta de Moebius

Comience con un cilindro circular infinita en posición vertical, un colector y sin límite. Cortar a través de ella de alta y baja para producir dos límites circulares, y la tira cilíndrica entre ellos. Esta es una variedad orientable con frontera, en la que "la cirugía" se llevará a cabo. Cortar la tira abierta, de modo que pudiera desenrollar para convertirse en un rectángulo, pero mantener un asimiento en los extremos cortados. Gire uno de los extremos 180 °, por lo que la cara superficie interna, y pegar los extremos de nuevo juntos sin problemas. Esto se traduce en una tira con una media torsión permanente: el Cinta de Moebius. Su límite ya no es un par de círculos, pero (topológicamente) un solo círculo; y lo que antes era su "interior" se ha fusionado con su "fuera", por lo que ahora sólo tiene un solo lado.

Botella de Klein

La botella Klein inmerso en el espacio tridimensional.

Tomar dos bandas de Möbius; cada uno tiene un solo bucle como un límite. Enderezar los bucles en círculos, y dejar que las tiras distorsionan en cruzadas gorras. Pegado de los círculos juntos producirá un nuevo colector cerrado sin límite, la botella de Klein . Cierre de la superficie no hace nada para mejorar la falta de capacidad de orientación, simplemente elimina el límite. Por lo tanto, la botella de Klein es una superficie cerrada sin distinción entre interior y exterior. Tenga en cuenta que en el espacio tridimensional, la superficie de una botella Klein debe pasar a través de sí mismo. La construcción de una botella de Klein que no se auto-intersección requiere cuatro o más dimensiones del espacio.

Plano proyectivo real

Comience con una esfera centrada en el origen. Cada línea que pasa por el origen perfora la esfera en dos puntos opuestos llamados antípodas . Aunque no hay manera de hacerlo físicamente, es posible combinar matemáticamente cada par antípoda en un solo punto. La superficie cerrada así producido es el plano proyectivo real, todavía otra superficie no orientable. Tiene una serie de descripciones y construcciones equivalentes, pero esta ruta explica su nombre: todos los puntos de cualquier línea dada a través del proyecto origen de la misma "punto" en este "plano".

Género y la característica de Euler

Durante dos colectores de dimensiones de una propiedad invariante clave es el género, o el "número de identificadores" presentes en una superficie. Un toro es una esfera con un mango, un doble toro es una esfera con dos asas, y así sucesivamente. De hecho, es posible caracterizar totalmente variedades compactas, de dos dimensiones sobre la base de género y orientabilidad. En colectores de dimensiones superiores género se sustituye por el concepto de característica de Euler .

Las generalizaciones de colectores

• Orbifolds : Un orbifold es una generalización del colector que permite ciertos tipos de " singularidades "en la topología. En términos generales, es un espacio que se ve a nivel local como los cocientes de un poco de espacio sencillo ( por ejemplo, el espacio euclidiano ) por las acciones de los diversos grupos finitos. Las singularidades se corresponden con puntos fijos de las acciones de grupo, y las acciones que deben ser compatibles en un cierto sentido.

• Variedades algebraicas y esquemas : variedades algebraicas no singulares sobre los números reales o complejos son colectores. Uno generaliza esta primera al permitir singularidades, en segundo lugar, al permitir diferentes campos, y en tercer lugar emulando la construcción de colectores de parcheo: así como un colector está pegado juntos desde subconjunto abierto del espacio euclidiano, una variedad algebraica se pega juntos a partir de variedades algebraicas afines, que son cero conjuntos de polinomios sobre campos algebraicamente cerrado. Esquemas son igualmente pegadas entre sí de los esquemas afines, que son una generalización de las variedades algebraicas. Ambos están relacionados con los colectores, pero se construyen algebraicamente utilizando poleas en lugar de los atlas.

Porque puntos singulares, una variedad es, en general, no es un colector, aunque lingüísticamente los francesesvariété, alemánMannigfaltigkeite Ingléscolectorson en gran parte sinónimos.en francés una variedad algebraica se llamaune algébrique variété(unavariedad algebraica), mientras que un múltiple liso se llamaune différentielle variété(unavariedad diferencial).

• CW-complejos : Un complejo CW es un espacio topológico formada pegando discos de diferente dimensionalidad juntos. En general, el espacio resultante es singular, y por lo tanto no un colector. Sin embargo, son de interés central en la topología algebraica, especialmente en teoría homotopy , ya que son fáciles de calcular con singularidades y no son una preocupación.