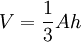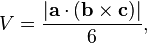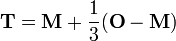Tetraedro

Temas relacionados: Matemáticas

Sabías ...

SOS Children, una organización benéfica educación , organizó esta selección. El patrocinio de los niños ayuda a los niños en el mundo en desarrollo para aprender también.

Tetraedro regular
(Haga clic aquí para el modelo de rotación)
Tipo	Sólidos platónicos
Elementos	F = 4, E = 6 V = 4 (χ = 2)
Las caras de los lados	4 {3}
Símbolo de Schläfli	{3,3} y s {2,2}
Símbolo Wythoff	3 \| 2 3 \| 2 2 2
Coxeter-Dynkin
Simetría	T _d, A _3, [3,3], (* 332)
Grupo de rotación	T, [3,3] ^+, (332)
Referencias	U _01, C _15, W ₁
Propiedades	Regular convexo Deltaedro
Ángulo diedro	70.528779 ° = arccos (1/3)
3.3.3 ( Vertex figura)	Auto-dual ( poliedro dual)
Neto

Un tetraedro (plural: los tetraedros) es un poliedro formado por cuatro triangulares caras, tres de los cuales se reúnen en cada vértice. Un tetraedro regular es uno en el que los cuatro triángulos son regulares, o "equilátero", y es uno de los sólidos platónicos .

El tetraedro es una especie de pirámide , el segundo tipo más común; una pirámide tiene una base plana, y las caras triangulares por encima de ella, pero la base puede ser de cualquier forma poligonal, no sólo cuadrada o triangular.

Como todo poliedros convexos, un tetraedro se puede plegar a partir de una sola hoja de papel.

Fórmulas para tetraedro regular

Para un tetraedro regular de longitud de borde $un$ :

Área de superficie	$A = a ^ 2 \ sqrt {3} \,$
Volumen	$V = \ begin {matriz} {1 \ over12} \ end {matriz} a ^ 3 \ sqrt {2} \,$
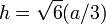Altura	$h = \ sqrt {6} (a / 3) \,$
Ángulo entre un borde y una cara	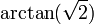$\ Arctan (\ sqrt {2}) \,$ (Aprox. 55 °)
Ángulo entre dos caras	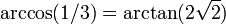$\ Arccos (1/3) = \ arctan (2 \ sqrt {2}) \,$ (Aprox. 71 °)
El ángulo entre los segmentos que unen el centro y los vértices	${\ Pi \ over 2} + \ arcsin (1/3) \,$ (Aprox. 109.471 °)
Ángulo sólido en un vértice subtendido por una cara	$3 \ arccos (1/3) - \ pi \,$ (Aprox. 0,55129 estereorradianes)
Radio de circumsphere	$R = \ sqrt {6} (a / 4) \,$
Radio de insphere que es tangente a las caras	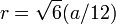$r = \ sqrt {6} (a / 12) \,$
Radio de midsphere que es tangente a los bordes	$r_M = \ sqrt {2} (a / 4) \,$
Radio de exspheres	$r_E = \ sqrt {6} (a / 6) \,$
Distancia al Exsphere centro desde un vértice	$\ Sqrt {6} (a / 2) \,$

Tenga en cuenta que con respecto al plano base de la pendiente de una cara ( $2 \ sqrt {2}$ ) Es el doble que la de un borde ( $\ Sqrt {2}$ ), Correspondiente al hecho de que la distancia horizontal cubierta desde la base hasta la ápice largo de un borde que es el doble de largo de la la mediana de un rostro. En otras palabras, si C es la centroide de la base, la distancia de C a un vértice de la base es el doble que la de C al punto medio de un borde de la base. Esto se deduce del hecho de que las medianas de un triángulo se cortan en su centroide, y este punto se divide cada uno de ellos en dos segmentos, uno de los cuales es el doble de largo que el otro (ver prueba).

Volumen de cualquier tetraedro

El volumen de cualquier tetraedro está dada por la fórmula del volumen pirámide:

$V = \ frac {1} {3} Ah \,$

donde A es el área de la base y h la altura desde la base hasta el ápice. Esto se aplica para cada una de las cuatro opciones de la base, por lo que las distancias de los vértices a las caras opuestas son inversamente proporcionales a las áreas de estas caras.

Para un tetraedro de vértices a = (a _1, a _2, a _3), b = _{(b1, b2, b3),} c = _{(c1, c2, c3),} y d = (d ₁ , d _2, d _3), el volumen es (1/6) · | det (a - b, b - c, c - d) |, o cualquier otra combinación de pares de vértices que forman un simplemente conectados gráfico. Esto se puede reescribir usando una producto escalar y producto vectorial , produciendo

$V = \ frac {| (\ mathbf {a} - \ mathbf {d}) \ cdot ((\ mathbf {b} - \ mathbf {d}) \ veces (\ mathbf {c} - \ mathbf {d}) ) |} {6}.$

Si se elige el origen del sistema de coordenadas para que coincida con el vértice d, entonces D = 0, por lo

$V = \ frac {| \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) |} {6},$

donde a, b, y C representan tres bordes que se juntan en un vértice, y $\ Mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c})$ es un triple producto escalar. La comparación de esta fórmula con que se utiliza para calcular el volumen de una paralelepípedo, llegamos a la conclusión de que el volumen de un tetraedro es igual a 1/6 del volumen de cualquier paralelepípedo que comparte con él tres bordes convergentes.

Cabe señalar que la triple escalar puede ser representado por las siguientes determinantes:

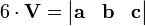$6 \ cdot \ mathbf {V} = \ begin {vmatrix} \ mathbf {a} y \ mathbf {b} y \ mathbf {c} \ end {vmatrix}$ o $6 \ cdot \ mathbf {V} = \ begin {vmatrix} \ mathbf {a} \\ \ mathbf {b} \\ \ mathbf {c} \ end {vmatrix}$ donde $\ Mathbf {a} = (a_1, a_2, a_3) \,$ se expresa como una fila o vector columna etc.

Por lo tanto

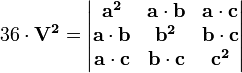$36 \ cdot \ mathbf {V ^ 2} = \ begin {vmatrix} \ mathbf {a ^ 2} & \ mathbf {a} \ cdot \ mathbf {b} y \ mathbf {a} \ cdot \ mathbf {c} \ \ \ mathbf {a} \ cdot \ mathbf {b} y \ mathbf {b ^ 2} & \ mathbf {b} \ cdot \ mathbf {c} \\ \ mathbf {a} \ cdot \ mathbf {c} & \ mathbf {b} \ cdot \ mathbf {c} & \ mathbf {c ^ 2} \ end {vmatrix}$ donde $\ Mathbf {a} \ cdot \ mathbf {b} = ab \ cos {C}$ etcétera

lo que da

$\ Mathbf {V} = \ frac {abc} {6} \ sqrt {1 + 2 \ cos {A} \ cos {B} cos {C} - \ cos ^ 2 {A} - \ cos ^ 2 {B} - \ cos ^ 2 {C}} \,$

Si nos dan sólo las distancias entre los vértices de cualquier tetraedro, entonces podemos calcular su volumen mediante la fórmula:

$288 \ cdot V ^ 2 = \ begin {vmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & d_ {12} ^ 2 & d_ {13} ^ 2 & d_ {14} ^ 2 \\ 1 y d_ {21} ^ 2 & 0 & d_ {23} ^ 2 & d_ {24} ^ 2 \\ 1 & d_ {31} ^ 2 & d_ {32} ^ 2 & 0 & d_ {34} ^ 2 \ \ 1 & d_ {41} ^ 2 & d_ {42} ^ 2 & d_ {43} ^ 2 & 0 \ end {vmatrix}.$

Si el valor del determinante es negativo, esto significa que no podemos construir un tetraedro con las distancias dadas entre los vértices.

Distancia entre los bordes

Cualquiera de los dos bordes opuestos de una mentira tetraedro en dos líneas oblicuas. Si el par más cercano de puntos entre estas dos líneas son puntos en los bordes, que definen la distancia entre los bordes; de otro modo, la distancia entre los bordes es igual a la que existe entre uno de los puntos finales y el borde opuesto.

Tres propiedades dimensionales de un tetraedro generalizada

Como con la geometría del triángulo, hay un conjunto similar de tres propiedades geométricas dimensionales para un tetraedro. Un tetraedro generalizada tiene un insphere, circumsphere, tetraedro medial y exspheres. Cuenta con centros respectivos, como incentro, circuncentro, excéntricas, Centro Spieker y puntos tales como un centroide. Sin embargo, hay, en general, no ortocentro en el sentido de altitudes de intersección. Hay una esfera equivalente a la triangular nueve punto círculo que es la circumsphere del tetraedro medial. Sin embargo, su circumsphere no lo hace, por lo general, pasar a través de los puntos de base de las altitudes del tetraedro referencia.

Para resolver estas inconsistencias, un centro sustituto conocido como el punto Monge que siempre existe para que se introduzca un tetraedro generalizada. Este punto fue identificado por primera vez por Gaspard Monge. Para tetraedros que la altitud no se cruzan, el punto de Monge y coinciden ortocentro. El punto Monge es definir como el punto donde los seis planos medios de un tetraedro se cruzan. Un plano medio se define como un plano que es ortogonal a un borde que une dos vértices que también contiene el centroide de un borde opuesto formado por la unión de los otros dos vértices.

Una línea ortogonal se redujo desde el punto Monge a cualquier cara es coplanar con otras dos líneas ortogonales a la misma cara. La primera es una altitud caído desde un vértice correspondiente a la cara elegida. La segunda es una línea ortogonal a la cara elegida que pasa por el ortocentro de esa cara. Esta línea ortogonal a través del punto Monge se encuentra a medio camino entre la altitud y la línea ortogonal orthocentric.

El punto, centroide Monge y circuncentro de un tetraedro son colineales y forman la recta de Euler del tetraedro. Sin embargo, a diferencia del triángulo, el centro de gravedad de un tetraedro se encuentra en el punto medio de su punto de Monge y circuncentro.

Hay una esfera equivalente a la triangular círculo de nueve puntos para el tetraedro generalizada. Es la circumsphere de su tetraedro medial. Es una esfera de doce puntos con centro en el circuncentro del tetraedro medial. Por definición que pasa a través de los centroides de las cuatro caras del tetraedro de referencia. Pasa a través de cuatro puntos de Euler de sustitución que se encuentran a una distancia de 1/3 de la distancia desde M, el punto de Monge, hacia cada uno de los cuatro vértices. Por último, pasa a través de los cuatro puntos de base de líneas ortogonales cayeron de cada punto de Euler a la cara que no contiene el vértice que genera el punto de Euler.

Si T representa este centro de doce puntos, entonces también se encuentra en la recta de Euler, a diferencia de su contraparte triangular, el centro se encuentra un tercio de la distancia desde M, el punto hacia el circuncentro Monge. También una línea ortogonal a través de T a una cara elegido es coplanar con otras dos líneas ortogonales a la misma cara. El primero es una línea ortogonal que pasa por el punto de Euler correspondiente a la cara elegida. La segunda es una línea ortogonal que pasa a través del centroide de la cara elegida. Esta línea ortogonal a través del centro de doce puntos se encuentra a medio camino entre la línea ortogonal punto de Euler y la línea ortogonal centroidal. Además, para cualquier cara, el centro de doce puntos se encuentra en el punto medio del punto de Euler correspondiente y el ortocentro de esa cara.

El radio de la esfera de doce puntos es 1/3 de la circunferencia circunscrita del tetraedro de referencia.

Si OABC forma un tetraedro generalizado con un vértice O como el origen y vectores $\ Mathbf {a}, \ mathbf {b} \,$ y $\ Mathbf {c} \,$ representar las posiciones de los vértices A, B y C con respecto a O, entonces el radio de la insphere está dada por:

$r = \ frac {6V} {| \ mathbf {b} \ times \ mathbf {c} | + | \ mathbf {c} \ times \ mathbf {a} | + | \ mathbf {a} \ times \ mathbf {b } | + | (\ mathbf {b} \ times \ mathbf {c}) + (\ mathbf {C} \ times \ mathbf {a}) + (\ mathbf {a} \ times \ mathbf {b}) |} \,$

y el radio de la circumsphere está dada por:

$R = \ frac {| \ mathbf {a ^ 2} (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b ^ 2} (\ mathbf {C} \ times \ mathbf {a}) + \ mathbf {c ^ 2} (\ mathbf {a} \ times \ mathbf {b}) |} {12V} \,$

que da el radio de la esfera de doce puntos:

$R_t = \ frac {| \ mathbf {a ^ 2} (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b ^ 2} (\ mathbf {c} \ times \ mathbf {a}) + \ mathbf {c ^ 2} (\ mathbf {a} \ times \ mathbf {b}) |} {36V} \,$

donde:

$6V = | \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) | \,$

El vector de posición de varios centros se dan de la siguiente manera:

El centroide

$\ Mathbf {G} = \ frac {\ mathbf {a} + \ mathbf {b} + \ mathbf {c}} {4} \,$

El circuncentro

$\ Mathbf {O} = \ frac {\ mathbf {a ^ 2} (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b ^ 2} (\ mathbf {c} \ times \ mathbf {a }) + \ mathbf {c ^ 2} (\ mathbf {a} \ times \ mathbf {b})} {12V} \,$

El punto Monge

$\ Mathbf {H} = \ frac {\ mathbf {a} \ cdot (\ mathbf {b} + \ mathbf {c}) (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b} \ cdot (\ mathbf {c} + \ mathbf {a}) (\ mathbf {c} \ times \ mathbf {a}) + \ mathbf {c} \ cdot (\ mathbf {a} + \ mathbf {b}) ( \ mathbf {a} \ times \ mathbf {b})} {12V} \,$

Las relaciones de línea de Euler son:

$\ Mathbf {G} = \ vec {H} + \ frac {1} {2} (\ mathbf {O} - \ mathbf {H}) \,$

$\ Mathbf {T} = \ vec {H} + \ frac {1} {3} (\ mathbf {O} - \ mathbf {H}) \,$

También debe tenerse en cuenta que:

$\ Mathbf {a} \ cdot \ mathbf {O} = \ frac {\ mathbf {a ^ 2}} {2} \ quad \ quad \ mathbf {b} \ cdot \ mathbf {O} = \ frac {\ mathbf { b ^ 2}} {2} \ quad \ quad \ mathbf {c} \ cdot \ mathbf {O} = \ frac {\ mathbf {c ^ 2}} {2} \,$

$\ Mathbf {a} \ cdot \ mathbf {H} = \ frac {\ mathbf {a} \ cdot (\ mathbf {b} + \ mathbf {c})} {2} \ quad \ quad \ mathbf {b} \ cdot \ mathbf {H} = \ frac {\ mathbf {b} \ cdot (\ mathbf {c} + \ mathbf {a})} {2} \ quad \ quad \ mathbf {c} \ cdot \ mathbf {H} = \ frac {\ mathbf {c} \ cdot (\ mathbf {a} + \ mathbf {b})} {2} \,$

Las relaciones geométricas

Un tetraedro es un 3- simplex. Al contrario que en el caso de otros sólidos platónicos, todos los vértices de un tetraedro regular son equidistantes entre sí (están en el único arreglo posible de cuatro puntos equidistantes).

Un tetraedro es un triangular pirámide, y el tetraedro regular es auto-dual.

Un tetraedro regular puede ser embebido dentro de un cubo de dos maneras de tal manera que cada vértice es un vértice del cubo, y cada borde es una diagonal de una de las caras del cubo. Por una de esas incrustación, la coordenadas cartesianas de la vértices son

(1, 1, 1);

(-1, -1, 1);

(-1, 1, -1);

(1, -1, -1).

Para el otro tetraedro (que es doble a la primera), invierta todos los signos. El volumen de este tetraedro es un tercio del volumen del cubo. La combinación de ambos tetraedros da un habitual compuesto poliédrica llama stella octangula, cuyo interior es un octaedro . Correspondientemente, un octaedro regular es el resultado de cortar, de un tetraedro regular, cuatro tetraedros regulares de la mitad del tamaño lineal (es decir, rectificar la tetraedro). La incrustación por encima divide el cubo en cinco tetraedros, uno de los cuales es regular. De hecho, 5 es el número mínimo de tetraedros requerido para componer un cubo.

La inscripción de tetraedros dentro de la normal compuesto de cinco cubos da dos más compuestos regulares, que contienen cinco y diez tetraedros.

Tetraedros regulares no pueden espacio teselado por sí mismos, aunque parece bastante probable que Aristóteles informó que era posible. Sin embargo, dos tetraedros regulares se puede combinar con un octaedro, dando una romboedro que puede espaciar azulejo.

Sin embargo, hay al menos un tetraedro irregular de copias que puede espacio azulejo. Si uno se relaja el requisito de que los tetraedros ser todos de la misma forma, se puede embaldosar el espacio utilizando sólo tetraedros de varias maneras. Por ejemplo, se puede dividir un octaedro en cuatro tetraedros idénticos y combinarlos de nuevo con dos regulares. (Como nota lateral: estos dos tipos de tetraedro tienen el mismo volumen.)

El tetraedro es único entre la poliedros uniformes en poseer ningún caras paralelas.

Poliedros Relacionados

Tetraedro truncado
Dos tetraedros en un cubo
Compuesto de cinco tetraedros
Compuesto de diez tetraedros

Tetraedros de intersección

Un poliedro interesante puede ser construido a partir cinco tetraedros de intersección. Este compuesto de cinco tetraedros se conoce desde hace cientos de años. Viene con regularidad en el mundo de origami. Unirse a los veinte vértices formaría un habitual dodecaedro. Hay tanto zurdo y formas diestro-que son imágenes especulares uno del otro.

Las isometrías del tetraedro regular

Las rotaciones adecuadas y reflexiones en el grupo de simetría del tetraedro regular

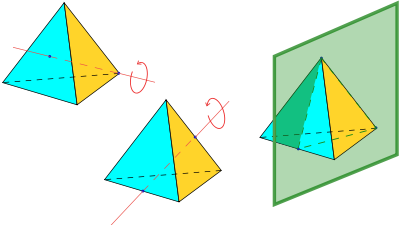
Los vértices de un cubo se pueden agrupar en dos grupos de cuatro, cada uno formando un tetraedro regular (ver más arriba, y también animación, que muestra uno de los dos tetraedros en el cubo). Las simetrías de un tetraedro regular corresponden a la mitad de las de un cubo: los que los tetraedros mapa a sí mismos, y no entre sí.

El tetraedro es el único sólido platónico que no se asigna a sí mismo por punto de inversión.

El tetraedro regular tiene 24 isometrías, formando la grupo de simetría T _d, isomorfo S _4. Se pueden clasificar de la siguiente manera:

T, isomorfo Un grupo alterna ₄ (la identidad y 11 rotaciones adecuadas) con la siguiente clases de conjugación (entre paréntesis se dan las permutaciones de los vértices, o correspondientemente, los rostros, y el unidad de representación cuaternión):
- identidad (identidad; 1)
- rotación alrededor de un eje que pasa por un vértice, perpendicular al plano opuesto, por un ángulo de ± 120 °: 4 ejes, 2 por eje, junto 8 ((1 2 3), etc .; (1 ± i ± ± j k) / 2)
- la rotación en un ángulo de 180 ° de manera que un mapas borde hasta el borde opuesto: 3 ((1 2) (3 4), etc .; i, j, k)
reflexiones en un plano perpendicular a un borde: 6
reflexiones en un plano combinado con 90 ° de rotación alrededor de un eje perpendicular al plano: 3 ejes, 2 por eje, junto 6; equivalentemente, son 90 ° rotaciones combinados con inversión (x se asigna a - x): las rotaciones se corresponden con los del cubo alrededor de ejes cara a cara

Las isometrías de tetraedros irregular

Las isometrías de un tetraedro irregular dependen de la geometría del tetraedro, con 7 casos posibles. En cada caso una Grupo de puntos de 3 dimensiones se forma.

Una base equilátero triángulo isósceles y (y no equilátero) lados del triángulo da 6 isometrías, correspondientes a los 6 isometrías de la base. Como permutaciones de los vértices, estos 6 isometrías son la identidad 1, (123), (132), (12), (13) y (23), formando el grupo de simetría C _3v, isomorfo a S _3.
Cuatro isósceles congruentes (no equiláteros) triángulos da 8 isometrías. Si los bordes (1,2) y (3,4) son de diferente longitud a la otra 4 entonces las 8 isometrías son la identidad 1, reflexiones (12) y (34), y 180 ° rotaciones (12) (34), (13) (24), (14) (23) e impropias 90 ° rotaciones (1234) y (1432) que forma el grupo de simetría D _2d.
Cuatro triángulos escalenos congruentes da 4 isometrías. Las isometrías son 1 y los 180 ° rotaciones (12) (34), (13) (24), (14) (23). Este es el Grupo de Klein V ₄ ≅ Z ₂ ^2, presente como el grupo de puntos de D _2.
Dos pares de isósceles isomórficas (no equiláteros) triángulos. Esto da dos bordes opuestos (1,2) y (3,4) que son perpendiculares longitudes pero diferentes, y luego el 4 isometrías son 1, reflexiones (12) y (34) y la rotación de 180 ° (12) (34) . El grupo de simetría es C _2v, isomorfo a V _4.
Dos pares de triángulos escalenos isomorfos. Esto tiene dos pares de bordes iguales (1,3), (2,4) y (1,4), (2,3) pero por lo demás no hay bordes iguales. Los únicos dos isometrías son 1 y la rotación (12) (34), dando el grupo C ₂ isomorfo a Z _2.
Dos isósceles desiguales triángulos con una base común. Esto tiene dos pares de bordes iguales (1,3), (1,4) y (2,3), (2,4) y de otra manera no hay bordes iguales. Las únicas dos isometrías son 1 y la reflexión (34), dando al grupo C _s isomorfo a Z _2.
No hay bordes iguales, por lo que la única isometría es la identidad, y el grupo de simetría es el grupo trivial.

Una ley de los senos para tetraedros y el espacio de todas las formas de tetraedros

Un corolario de lo habitual ley de los senos es que en un tetraedro cuyos vértices O, A, B, C, tenemos

$\ Ángulo OAB pecado \ \ cdot \ sin \ ángulo OBC \ cdot \ sin \ ángulo OCA = \ sin \ ángulo OAC \ cdot \ sin \ ángulo OCB \ cdot \ sin \ ángulo OBA. \,$

Uno puede ver las dos caras de esta identidad como correspondiente a las agujas del reloj y en sentido contrario orientaciones de la superficie.

Poner cualquiera de los cuatro vértices en el papel de O produce cuatro de tales identidades, pero en un sentido como máximo tres de ellos son independientes: Si se multiplican los lados "hacia la derecha" de tres de ellos y el producto se infiere a ser igual a la producto de las partes "en sentido contrario" de los mismos tres identidades, y luego los factores comunes se cancelan desde ambos lados, el resultado es el cuarto identidad. Una de las razones para estar interesado en esta relación "independencia" es la siguiente: Es ampliamente conocido que tres ángulos son los ángulos de algunos triángulo si y sólo si su suma es un semicírculo. ¿Qué condición en 12 ángulos es necesaria y suficiente para que sean los 12 ángulos de algunos tetraedro? Es evidente que la suma de los ángulos de cualquier lado de la tetraedro debe ser un medio círculo. Puesto que hay cuatro de estos triángulos, hay cuatro de tales limitaciones en sumas de ángulos, y el número de grados de libertad, reduciéndose así de 12 a 8. Los cuatro relaciones establecidas en la presente ley de los senos reducir aún más el número de grados de libertad, no de 8 a 4, pero sólo a partir de 8 a 5, ya que la cuarta restricción no es independiente de los tres primeros. Así, el espacio de todas las formas de tetraedros es 5-dimensional.

Usos Computacional

Las formas complejas a menudo se descomponen en un de malla de tetraedros irregular en la preparación de análisis de elementos finitos y computacionales estudios de dinámica de fluidos.

Aplicaciones y usos

La ion amonio es tetraédrica

Varias de las piezas de puntuación Tetraedro y partidos desde el 2005 Juego FIRST Robotics Competition

Embalaje

La empresa Tetra Classic de Tetrapak está en la forma de un tetraedro.

Química

La forma de tetraedro es visto en la naturaleza en los enlaces covalentes de las moléculas. Por ejemplo, en una metano molécula (CH ₄₎ los cuatro átomos de hidrógeno se encuentran en cada esquina de un tetraedro con el átomo de carbono en el centro. Por esta razón, una de las principales revistas de química orgánica es llamado Tetraedro. El amonio es otro ejemplo.
Ángulo desde el centro hacia dos vértices es $\ arccos {\ left (- \ tfrac {1} {3} \ right)}$ , o aproximadamente 109.47 °.

Electrónica

Si cada borde de un tetraedro se sustituyese por un uno ohm resistencia, la resistencia entre dos vértices sería 1/2 ohm.

Simbolismo

El tetraedro representa el elemento clásica fuego.

Juegos

Especialmente en de rol, este sólido se conoce como un d4 , uno de los más comunes los dados poliédricos .
Tetraedros construidos de 1 1/4 " Tubo de PVC, que eran conocidos como 'tetras, se utiliza como objeto principal de puntuación en el 2005 Juego FIRST Robotics Competition Triple Play. El objetivo del juego era para apilar estos "tetras" en metas más grandes tetraedro que aquí colocan en una matriz de 3 × 3.
Algunos de cubo de Rubik rompecabezas -como son tetraédricos, como el Pyraminx y Pyramorphix.
Cabeza de la pirámide de la Silent Hill de juegos tiene una tetraédrica en la parte superior de la cabeza.

Ficción

En el Secuencia de Xeelee libros de ciencia ficción de la autora Stephen Baxter, un tetraedro azul-verde es el símbolo de la libertad de la humanidad.
La Triforces de la Leyenda de Zelda serie de dibujos animados son tetraedros verdes y rojos. La representación de la Trifuerza de la serie juego real (a partir de A Link to the Past) es la de un tetraedro desplegada.
El arco de la historia de la serie fan de "Star Trek: Hidden Frontier "gira en torno a gigantescos artefactos antiguos, que más tarde se convierten en una parte central de la serie. Los artefactos se refiere como tetraedros y tienen la forma de un cuerpo tan geométrica. En la serie, los tetraedros poseen la capacidad de producir una gran cantidad de energía y son de material desconocido y origen, sin embargo, parecen ser varios millones de años de antigüedad y se detallan que estos dispositivos han sido construidas por una civilización antigua.

Recuperado de " http://en.wikipedia.org/w/index.php?title=Tetrahedron&oldid=205612904 "

Home Page - YouTube Channel