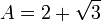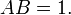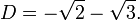Teoria de Galois

Évariste Galois (1811-1832)

Em matemática , mais especificamente em álgebra abstrata , a teoria de Galois, nomeada após Évariste Galois, fornece uma conexão entre teoria de campo e teoria do grupo . Usando a teoria de Galois, certos problemas na teoria de campo pode ser reduzido a teoria do grupo, que é, em certo sentido mais simples e melhor compreendido.

Originalmente usado Galois grupos de permutação para descrever como as várias raízes de uma dada polinomial equação estão relacionados uns com os outros. A abordagem moderna à teoria de Galois, desenvolvido por Richard Dedekind, Leopold Kronecker e Emil Artin, entre outros, envolve o estudo automorfismos de extensões de campo.

Além disso abstração da teoria de Galois é alcançada pela teoria da Conexões de Galois.

Aplicação aos problemas clássicos

O nascimento da teoria de Galois foi originalmente motivado pela seguinte pergunta, cuja resposta é conhecida como a Abel-Ruffini teorema.

"Por que não há fórmula para as raízes de um quinto (ou superior) equação polinomial grau em termos dos coeficientes do polinômio, usando apenas as operações habituais algébricas (adição, subtração, multiplicação, divisão) e aplicação de radicais (raízes quadradas , raízes cúbicas, etc)? "

Teoria de Galois não só proporciona uma bela resposta a esta pergunta, ele também explica detalhadamente por que é possível para resolver equações de grau quatro ou mais baixa na forma acima, e por suas soluções de assumir a forma que eles fazem. Além disso, ele dá um meio conceitualmente claros, práticos e muitas vezes, de dizer quando alguma equação particular de grau mais elevado pode ser resolvido dessa forma.

Teoria de Galois também dá uma clara visão sobre questões relativas aos problemas em régua e compasso construção. Dá uma caracterização elegante dos rácios de comprimentos que podem ser construídos com este método. Com isso, torna-se relativamente fácil de responder a tais problemas clássicos da geometria como

"Quais regulares polígonos são polígonos constructible? "

"Por que não é possível trissecar todos os ângulos? "

História

Teoria de Galois originado no estudo de funções simétricas - os coeficientes de um polinômio são (até assinar) o polinômios simétricos elementares nas raízes. Por exemplo, (x - a) (x - b) x = ² - (a + b) x + AB, em que 1, a + b e ab são os polinómios elementares de grau 0, 1 e 2, em duas variáveis.

Este foi formalizado pela primeira vez pelo matemático francês do século 16 François Viète, em Fórmulas de Viète, para o caso de raízes reais positivos. Na opinião do matemático britânico do século 18 Charles Hutton, a expressão de coeficientes de um polinómio em termos das raízes (não somente para as raízes positivas) foi primeiro entendido pelo matemático francês do século 17 Albert Girard; Hutton escreve:

... [Girard era] a primeira pessoa que compreendeu a doutrina geral de formação dos coeficientes das potências da soma das raízes e seus produtos. Ele foi o primeiro que descobriu as regras para somar as potências das raízes de qualquer equação.

Nesse sentido, o discriminante é uma função simétrica nas raízes que reflecte as propriedades de as raízes - é zero, se e apenas se o polinómio tem uma raiz múltipla, e para polinómios quadráticos e cúbicos é positivo se e apenas se todas as raízes são reais e distinto, e negativo se e somente se houver um par de raízes complexos conjugados distintos. Ver Discriminante: a natureza das raízes para detalhes.

O primeiro cúbico foi parcialmente resolvido até o dia 15 / matemático italiano do século 16 Scipione del Ferro, que, contudo, não publicar seus resultados; este método só resolveu uma das três classes, como os outros envolvidos, tendo raízes quadradas de números negativos e números complexos não eram conhecidos na época. Esta solução foi, em seguida, reencontrada independentemente em 1535 por Niccolò Fontana Tartaglia, que compartilhou com Gerolamo Cardano, pedindo-lhe para não publicá-lo. Cardano, em seguida, estendeu isso para os outros dois casos, utilizando raízes quadradas de negativos como passos intermédios; veja detalhes em O método de Cardano. Após a descoberta do trabalho de Ferro, ele sentiu que o método de Tartaglia não era mais segredo, e, assim, ele publicou sua solução completa em sua 1545 Ars Magna. Seu aluno Lodovico Ferrari resolveu o polinomial quártica, que Cardano solução também incluiu em Ars Magna.

Um outro passo foi o papel 1770 Reflexões sobre a résolution algébrique des équations pelo matemático francês-italiano Joseph Louis Lagrange , em seu método de Resolventes Lagrange, onde analisou a solução de Cardano e Ferrarri de cúbicas e quárticas por considerá-los em termos de permutações das raízes, que renderam um polinômio auxiliar de menor grau, proporcionando um entendimento unificado das soluções e estabelecer as bases para a teoria do grupo e Galois teoria. Fundamentalmente, no entanto, ele não considerou composição de permutações. O método de Lagrange não se estendia às equações de quinto grau ou superior, porque o resolvent teve maior grau.

O quintic foi quase provado que não têm soluções gerais por radicais por Paolo Ruffini em 1799 , cuja introspecção chave era usar grupos de permutação, e não apenas uma única permutação. Sua solução continha uma lacuna, que Cauchy consideradas menores, embora isso não foi corrigida até que o trabalho do matemático norueguês Niels Henrik Abel, que publicou uma prova em 1824, estabelecendo assim o Abel-Ruffini teorema.

Enquanto Ruffini e Abel estabelecido que o quintic geral não pode ser resolvido, alguns quintics particulares podem ser resolvidos, tais como (x - 1) ^5, e o critério preciso pelo qual um dado polinomial quintic ou superior pode ser determinado como sendo ou não solúvel foi dada por Évariste Galois, que mostrou que se um polinômio era solúvel ou não era equivalente à existência ou não do grupo de permutação de suas raízes - em termos modernos, o seu Grupo de Galois - tinha uma certa estrutura - em termos modernos, ou não era um grupo solucionável. Este grupo foi sempre solucionáveis por polinômios de grau quatro ou menos, mas nem sempre isso por polinômios de grau cinco e maior, o que explica por que não há solução geral em maior grau.

A abordagem do grupo de permutações a teoria de Galois

Dado um polinómio, pode ser que algumas das raízes estão ligados por vários equações algébricas. Por exemplo, pode ser que para duas das raízes, por exemplo A e B, que A ² 5 B + ³ = 7. A ideia central da teoria de Galois é considerar essas permutações (ou rearranjos) das raízes tendo a propriedade de que qualquer equação algébrica satisfeita com as raízes ainda está satisfeito após as raízes foram permutados. Uma ressalva importante é que nós nos restringir às equações algébricas cujos coeficientes são números racionais . (Uma vez pode especificar um certo campo em que os coeficientes devem mentir, mas, para os exemplos simples abaixo, vamos nos restringir ao campo de números racionais.)

Estas permutações em conjunto formam um grupo de permutação, também chamado de Grupo de Galois do polinômio (sobre os números racionais). Para ilustrar este ponto, considere os seguintes exemplos:

Primeiro exemplo - uma equação quadrática

Considere a equação quadrática

Ao usar a fórmula quadrática , descobrimos que as duas raízes são

Exemplos de equações algébricas satisfeitas por A e B incluem

e

Obviamente, em qualquer uma destas equações, se trocamos A e B, obtemos uma outra afirmação verdadeira. Por exemplo, a equação A + B = 4 torna-se simplesmente B + A = 4. Além disso, ela é verdadeiro, mas muito menos óbvio, que esta tem para cada possível equação algébrica com racional coeficientes satisfeitas pelo raízes A e B; para provar isso requer a teoria de polinômios simétricos.

Conclui-se que o grupo de Galois do polinómio x ^2-4 x + 1 consiste de duas permutações: a identidade de permutação que folhas A e B intacto, e o permutação que troca transposição A e B. É um grupo cíclico de ordem dois, e, por conseguinte, isomorfo a Z / 2 Z.

Pode-se objetar que A e B estão relacionados por mais uma equação algébrica,

que não permanece verdadeiro quando A e B são trocados. Contudo, esta equação não nos interessa, uma vez que não têm coeficientes racionais; em particular, é não racional.

Uma discussão semelhante aplica-se a qualquer polinomial quadrática ax ² + bx + c, onde a, b e c são números racionais.

• Se o polinómio tem apenas uma raiz, por exemplo, x ^2-4 x + 4 = (x-2) ^2, em seguida, o grupo de Galois é trivial; isto é, que contém apenas a permutação de identidade.
• Se tem duas raízes racionais distintas, por exemplo x ^2-3 x + 2 = (x-2) (x-1), o grupo de Galois é novamente trivial.
• Se tem duas raízes irracionais (incluindo o caso em que as raízes são complexo ), em seguida, o grupo de Galois contém duas permutações, tal como no exemplo acima.

Segundo exemplo

Considere o polinômio

que também pode ser escrito como

Nós desejamos descrever o grupo de Galois deste polinômio, novamente sobre o campo de números racionais . O polinômio tem quatro raízes:

Existem 24 possíveis maneiras para permutar estes quatro raízes, mas não todas estas permutações são membros do grupo de Galois. Os membros do grupo de Galois deve preservar qualquer equação algébrica com coeficientes racionais envolvendo A, B, C e D. Uma tal equação é

A + D = 0.

No entanto, desde

,

a permutação

(A, B, C, D) → (A, B, D, C)

Não é permitido (porque ele transforma a equação válida A + D = 0 na equação inválido A + C = 0).

Outra equação que as raízes é satisfazer

Isto irá excluir outras permutações tais como,

(A, B, C, D) → (A, C, B, D).

Continuando desta maneira, vemos que as únicas permutações (que satisfaçam ambas as equações simultaneamente) restantes são

(A, B, C, D) → (A, B, C, D)

(A, B, C, D) → (C, D, A, B)

(A, B, C, D) → (B, A, D, C)

(A, B, C, D) → (D, C, B, A),

eo grupo de Galois é isomorfo ao Klein quatro grupo.

A abordagem moderna pela teoria de campo

Na abordagem moderna, começa-se com um campo de extensão L / K (leia-se: L sobre K), e examina o grupo de campo automorphisms de L / K (estes são mapeamentos α: L → L com α (x) = x para todos os x em K). Veja o artigo sobre Grupos de Galois para mais explicações e exemplos.

A ligação entre as duas abordagens é a seguinte. Os coeficientes do polinômio em questão deve ser escolhido a partir do campo base de K. O campo superior L deve ser o campo obtido por adjacente as raízes do polinômio em questão para o campo base. Qualquer permutação das raízes que respeita equações algébricas como acima descrito dá origem a uma automorphism de L / K, e vice-versa.

No primeiro exemplo acima, estávamos estudando a extensão Q (√3) / Q, em que Q é o campo de números racionais , e Q (√3) é o campo obtidos a partir de Q por √3 adjacente. No segundo exemplo, que estavam a estudar a extensão Q (A, B, C, D) / Q.

Existem várias vantagens para a abordagem moderna sobre a abordagem do grupo de permutações.

• Ele permite que uma declaração muito mais simples do teorema fundamental da teoria de Galois.
• O uso de outros campos da base do que Q é crucial em muitas áreas da matemática. Por exemplo, em teoria dos números algébricos, sempre ocorre usando a teoria de Galois campos de números, campos de finitos ou campos de locais como o campo base.
• Ele permite que se estude mais facilmente extensões infinitas. Novamente, isto é importante na teoria dos números algébricos, onde, por exemplo, um muitas vezes discute a grupo absoluta de Galois de Q, definido como sendo o grupo de Galois de K / Q em que K é um fecho algébrico de Q.
• Ela permite a consideração de extensões inseparáveis. Este problema não se coloca no quadro clássico, desde que foi sempre assumido implicitamente que a aritmética teve lugar em característica zero, mas característica diferente de zero surge frequentemente na teoria dos números e em geometria algébrica.
• Ele remove a dependência em vez artificial em perseguir raízes de polinômios. Ou seja, diferentes polinômios pode produzir os mesmos campos de extensão, ea abordagem moderna reconhece a ligação entre estes polinômios.

Grupos solúveis e solução por radicais

A noção de um grupo solucionável na teoria do grupo permite determinar se um polinômio é solúvel nos radicais, dependendo se seu grupo de Galois tem a propriedade de solvabilidade. Na sua essência, cada campo de extensão L / K corresponde a um grupo em um fator série composição do grupo de Galois. Se um grupo fator na série composição é cíclico de ordem n, em seguida, se o campo de extensão correspondente é uma extensão de um campo que contém um raiz primitiva da unidade, então isso é uma extensão radical, e os elementos de L pode então ser expresso utilizando a n-ésima raiz de um elemento de K.

Se todos os grupos de factor na sua composição são série cíclico, o grupo de Galois é chamado solúvel, e todos os elementos do campo correspondente pode ser encontrado tomando repetidamente raizes, produtos e somas de elementos a partir do campo de base (normalmente Q) .

Um dos grandes triunfos da Teoria de Galois foi a prova de que para cada n> 4, existem polinômios de grau n que não são solucionáveis por radicais-o Abel-Ruffini teorema. Isto é devido ao facto de, para n> 4 o simétrica grupo S _n contém um simples, não-cíclico, subgrupo normal.

O polinômio . A verdadeira raiz solitário = 1,1673 ... é algébrica, mas não exprimível como radicais. Os outros quatro raízes são números complexos .

Um exemplo quintic não-solucionáveis

Van der Waerden cita o polinômio . Pelo teorema raiz racional não tem zeros racionais. Também não tem fatores lineares módulo 2 ou 3.

tem a fatoração modulo 2. Isso significa que seu grupo Galois modulo 2 é cíclico de ordem 6.

não tem fator modulo quadrático 3. Assim seu grupo Galois modulo 3 tem ordem 5.

Sabemos que um grupo de Galois módulo um primo é isomorfo a um subgrupo do grupo de Galois sobre os racionais. Um grupo de permutação em 5 objetos com operações de ordem 6 e 5 deve ser o grupo simétrico , O que deve ser o grupo de Galois . Este é um dos exemplos mais simples de um polinômio do quinto grau não-solucionáveis. Serge Lang disse que Artin estava apaixonado por este exemplo.

O inverso problema Galois

Todos os grupos finitos ocorrem como grupos de Galois. É fácil de construir extensões de campo com qualquer grupo finito dada como grupo de Galois, contanto que não se também especificar o campo de terra.

Para isso, escolha o campo K e um grupo finito G. O teorema de cayley diz que G é (até isomorfismo) um subgrupo de a simétrica grupo S sobre os elementos de L. Escolha indeterminadas {x} _α, um para cada elemento de α L, e contíguo ao K-los para obter o campo F = K ({x} _α). Contidos dentro do campo F é L de simétrico funções racionais no {x} _α. O grupo de Galois de F / L é S, por um resultado básico de Emil Artin. G age em M por restrição de ação da S. Se o campo fixo desta acção é M, em seguida, pelo teorema fundamental da teoria de Galois, o grupo de Galois de F / M é G.

É um problema em aberto para revelar a existência de uma extensão de campo do campo racional Q com um determinado grupo finito como grupo de Galois. Hilbert desempenhado um papel na resolução do problema para todos os grupos simétricos e alternadas. Igor Shafarevich provou que todos os grupos finitos solúvel é o grupo de Galois de alguma extensão de Q. Várias pessoas têm resolvido o problema Galois inversa para selecionado não abeliano grupos simples. A existência de soluções foi mostrado para todos, mas possivelmente um ( Mathieu grupo H ₂₃₎ dos 26 grupos simples esporádicos. Há até mesmo um polinômio com coeficientes inteiros cujo grupo de Galois é o Grupo Monstro.