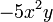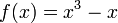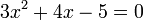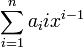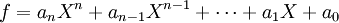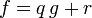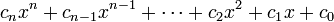Polinomial

Em matemática , um polinômio é uma expressão que é construída a partir de um ou mais e variáveis constantes, utilizando apenas as operações de adição, subtração, multiplicação e de números inteiros positivos expoentes constantes. Por exemplo, é um polinômio, mas não é um polinómio porque envolve a divisão por uma variável e porque tem um expoente que não é um número inteiro positivo.

Polinômios são um dos conceitos mais importantes em álgebra e em toda a matemática e ciências. Eles podem ser usados para formar equação polinomial, que pode codificar uma grande variedade de problemas, desde elementar problemas de história para problemas complicados nas ciências; eles podem ser usados para definir as funções polinomiais, que aparecem nas definições que variam de base química e física para a economia , e são utilizados no cálculo e análise numérica para aproximar outras funções. Polinômios são usados em seu próprio direito de construir anéis de polinômios, um dos conceitos mais poderosos da álgebra e geometria algébrica.

Visão global

Um polinómio é zero, ou pode ser escrita como a soma de um ou mais diferente de zero termos. O número de termos é finito. Estes consistem termos de uma constante (o chamado coeficiente do termo) multiplicado por zero ou mais variáveis (que geralmente são representados por letras). Cada variável pode ter um expoente que é um número inteiro não negativo. O expoente de uma variável num prazo é igual ao de grau variável em que esse termo. Desde , O grau de uma variável sem um expoente é escrito um. Um termo com nenhuma variável é chamado de termo constante, ou apenas uma constante. O grau de um termo constante é 0. O coeficiente de um termo pode ser qualquer número, incluindo frações, números irracionais, os números negativos e números complexos.

Por exemplo,

é um termo. O coeficiente é de -5, as variáveis são X e Y, o grau de x é dois, e o grau de y é um.

O grau de todo o termo é a soma dos graus de cada variável na mesma. No exemplo acima, o grau é 2 + 1 = 3.

Um polinômio é uma soma de termos. Por exemplo, o seguinte é um polinômio:

É composto de três termos: o primeiro é o grau dois, o segundo é um grau, e o terceiro é de zero graus. Aqui "

"Significa"

", De modo que o coeficiente do termo médio é de -5.

Quando um polinômio em uma variável está disposta na ordem tradicional, os termos de maior grau vir antes os termos de menor grau. No primeiro termo acima, o coeficiente é 3, x é a variável, e é o expoente 2. No segundo termo, o coeficiente é de -5. O terceiro termo é uma constante. O grau de um polinômio não zero é o maior grau de qualquer prazo. No exemplo, o grau polinomial tem dois.

Formas alternativas

Uma expressão que pode ser convertido para a forma polinomial através de uma sequência de aplicações do comutativa , associativa , e leis distributivas é geralmente considerado como um polinômio. Por exemplo

é um polinômio, porque ele pode ser trabalhado para 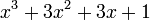. Similarmente

é considerado um período de validade de um polinómio, embora envolva uma divisão, uma vez que é equivalente a e é apenas uma constante. O coeficiente de este termo, por conseguinte, . Por razões semelhantes, se coeficientes complexos são permitidos, um muitos têm um único mandato como ; embora parece que ele deve ser trabalhado para dois termos, o complexo número 2 + 3 i é na verdade apenas um coeficiente único neste caso que acontece a exigir um "+" para ser escrito para baixo.

Divisão por uma expressão contendo uma variável geralmente não é permitido em polinômios. Por exemplo,

não é um polinómio porque inclui a divisão por uma variável. Da mesma forma,

não é um polinómio, porque tem um expoente variável.

Desde subtracção pode ser tratada como a adição do aditivo oposto, e uma vez que a exponenciação a uma potência constante de número inteiro positivo pode ser tratada como a multiplicação repetida, polinómios pode ser construído a partir de constantes e variáveis, com apenas duas operações de adição e multiplicação.

Funções polinomiais

A função polinomial é uma função definida por avaliação de um polinômio. Por exemplo, a função F, tendo números reais de números reais, definido pela

é uma função polinomial de uma variável. Funções polinomiais também pode ser definido pelo uso de polinômios em múltiplas variáveis, como em

.

Funções polinomiais são uma importante classe de funções suaves.

Equações polinomiais

Uma equação polinomial é uma equação em que um polinómio é ajustado igual a um outro polinómio.

é uma equação polinomial.

Propriedades elementares de polinômios

1. A soma de polinômios é um polinômio
2. A produto de polinômios é um polinômio
3. O derivado de uma função polinomial é uma função polinomial
4. Qualquer primitivo ou antiderivada de uma função polinomial é uma função polinomial

Polinômios servir para aproximar outras funções , tais como seno, cosseno , e exponencial .

Todos os polinómios tem uma forma expandida, na qual o lei de distribuição tem sido utilizado para remover todos os parênteses. Todos os polinômios têm também uma forma consignada em que o polinômio é escrito como um produto de polinômios lineares. Por exemplo, o polinómio

é a forma expandida do polinômio

,

que é escrito em forma fatorada. Note-se que as constantes nas polinómios lineares (como -3 e +1 no exemplo acima) pode ser números complexos em certos casos.

Em álgebra escola, os alunos aprendem a mover-se facilmente de uma forma para outra (ver: factoring ).

Cada polinómio em uma variável é equivalente a uma polinomial com o formulário

.

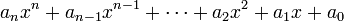Esta forma é por vezes tomada como a definição de um polinômio em uma variável.

Avaliação de um polinômio consiste em atribuir um número a cada variável e no cumprimento das multiplicações e adições indicadas. A avaliação é, por vezes, realizada de forma mais eficiente usando o Esquema de Horner

.

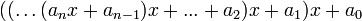Em elementar álgebra , os métodos são dadas para a solução de todos os de primeiro grau e segundo grau equações polinomiais em uma variável. No caso de equações polinomiais, a variável é freqüentemente chamado de um desconhecido. O número de soluções não pode exceder o grau, e será igual ao grau quando multiplicidade de soluções e números complexos soluções são contados. Este facto é chamado o teorema fundamental da álgebra.

Um sistema de equações polinomiais é um conjunto de equações em que uma dada variável devem ter o mesmo valor sempre que aparece em qualquer uma das equações. Sistemas de equações são geralmente agrupados com uma única chave de abertura do lado esquerdo. Em álgebra elementar , os métodos são dadas para resolver um sistema de equações lineares em várias incógnitas. Para obter uma solução única, o número de equações deve ser igual ao número de incógnitas. Se houver mais do que incógnitas equações, o sistema é chamado subdeterminada . Se houver mais do que equações incógnitas, o sistema é chamado sobredeterminado. Este assunto importante é estudada extensivamente na área da matemática conhecido como álgebra linear . Sobredeterminadas sistemas são comuns em aplicações práticas. Por exemplo, uma pesquisa de mapeamento dos EUA usou computadores para resolver equações de 2,5 milhões em 400 mil incógnitas.

Os exemplos mais avançados de polinômios

Em álgebra linear , o polinomial característica de uma matriz quadrada codifica várias propriedades importantes da matriz .

Em a teoria dos grafos polinomial cromática de um gráfico codifica as diferentes formas de vértice colorir o gráfico usando x cores.

Em álgebra abstrata , pode-se definir polinômios com coeficientes em qualquer anel.

Em teoria dos nós do Alexander polinomial, o Polinomial Jones, eo HOMFLY polinomial são importantes invariantes nó.

História

Determinar as raízes de polinômios, ou "resolução de equações algébricas", é um dos problemas mais antigos de matemática. No entanto, a notação elegante e prático que usamos hoje só se desenvolveu a partir do século 15. Antes disso, as equações são escritas em palavras. Por exemplo, um problema de álgebra dos chineses Aritmética em nove seções, circa 200 aC, começa "Três polias de boa colheita, duas polias de colheita medíocre, e um maço de má colheita são vendidos para 29 dou." Podemos escrever .

Notação

O primeiro uso conhecido do sinal de igual é em De Robert Recorde The Whetstone de Witte, 1557. A sinais + para adição, - para subtração, eo uso de uma carta para um desconhecido aparecer em De Michael Stifel Arithemetica integra, 1544. René Descartes, em La geometrie, 1637, introduziu o conceito do gráfico de uma equação polinomial. Ele popularizou a utilização de cartas a partir do início do alfabeto para denotar constantes e as cartas a partir do final do alfabeto para denotar variáveis, como pode ser visto acima, na fórmula geral para um polinómio de uma variável, sendo que um 's representar constantes e x denota uma variável. Descartes introduziu a utilização de sobrescritos para denotar expoentes bem.

Resolvendo equações polinomiais

A cada polinomiais corresponde a uma função polinomial, em que f (x) é definido como igual ao polinomial, e de uma equação polinomial, onde o polinómio é definida igual a zero. As soluções para a equação são chamadas as raízes do polinômio e eles são os zeros da função e os X-interceptações de seu gráfico. Se x = a é uma raiz de um polinómio, então (x - a) é um factor de que polinomial.

Alguns polinômios, como f (x) = x ² + 1, não têm qualquer raízes entre os números reais . Se, no entanto, o conjunto de candidatos desejados é expandido para os números complexos , cada (não constante) polinomial tem pelo menos uma raiz distinta; esta situação decorre do teorema fundamental da álgebra.

Há uma diferença entre a aproximação raízes e encontrar raízes exatas. Fórmulas para as raízes de polinômios até um grau de 2 são conhecidas desde tempos antigos (ver equação quadrática ) e até um grau de 4 desde o século 16 (ver Gerolamo Cardano, Niccolo Fontana Tartaglia). Mas fórmulas para grau 5 iludiu os pesquisadores. Em 1824, Niels Henrik Abel provou o resultado surpreendente de que não pode haver nenhuma fórmula geral (envolvendo apenas as operações aritméticas e radicais) para as raízes de um polinômio de grau 5 ou superior em termos de seus coeficientes (veja Teorema de Abel-Ruffini). Este resultado marcou o início da teoria de Galois , que se engaja em um estudo detalhado das relações entre raízes de polinômios.

Resolver numericamente uma equação polinomial em um desconhecido é feito facilmente no computador pelo Método Durand-Kerner ou por alguma outra algoritmo de apuramento de raiz. A redução de equações em várias equações para incógnitas em cada um desconhecido é discutido no artigo sobre o Algoritmo de Buchberger. O caso especial onde todos os polinômios são de grau um é chamado de um sistema de equações lineares , para a qual uma gama de diferentes métodos de solução existe, incluindo o clássico eliminação de Gauss .

Foi demonstrado por Richard Birkeland e Karl Meyr que as raízes de qualquer polinomial pode ser expressa em termos de multivariada funções hipergeométricas. Ferdinand von Lindemann e Hiroshi Umemura mostraram que as raízes podem também ser expressos em termos de Funções modulares Siegel, generalizações do funções teta que aparecem na teoria da funções elípticas. Estas caracterizações das raízes de polinómios arbitrários são generalizações dos métodos previamente descoberto para resolver o equação do quinto grau.

Gráficos

Uma função polinomial de uma variável real pode ser representado por um grafo.

• O gráfico do polinômio de zero

f (x) = 0

é o eixo x.

• O gráfico de um polinômio grau 0

f (x) = a _0, onde a ₀ ≠ 0,

é uma linha horizontal com y -intercept um ₀

• O gráfico de um polinômio grau 1 (ou função linear)

f (x) = A + a _{1 0} x, em que um ₁ ≠ 0,

é uma linha oblíqua com y -intercept a ₀ e uma inclinação _1.

• O gráfico de um polinômio grau 2

f (x) = a + ₀ um ₁ x + a ₂ x ^2, onde um ₂ 0 ≠

é um parábola.

• O gráfico de qualquer polinômio com grau 2 ou superior

f (x) = a + ₀ um ₁ x + a ₂ x ² +. . . + A _n x ^n, em que _n um ≠ 0 e n 2 ≥

é uma curva não linear contínuo.

Gráficos de polinômios são analisados no cálculo usando interceptações, encostas, concavidade e comportamento final.

As ilustrações abaixo mostrar gráficos de polinômios.

Polinômio de grau 2: f (x) = x 2 - x - 2 = (X 1), (x-2)	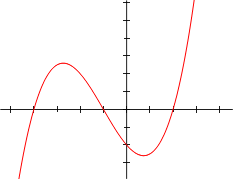Polinômio de grau 3: f (x) = x 3/5 x 2 + 4/5 - 7 x / 5-2 = 1/5 (5 x) (x 1), (x-2)
Polinômio de grau 4: f (x) = 1/14 (4 x) (x 1), (x-1) (X-3) + 0,5	Polinômio de grau 5: f (x) = 1/20 (x 4) (2 x) (x 1), (x-1) (X-3) + 2

Polinômios e cálculo

Um aspecto importante do cálculo é o projeto de análise de funções complicadas por meio de aproximar-los com polinômios. O auge desses esforços é o teorema de Taylor , que afirma que aproximadamente a cada função diferenciável localmente parece um polinômio, eo Teorema de pedra-Weierstrass, que afirma que todos os função contínua definida em um compacto intervalo do eixo real pode ser aproximada em todo o intervalo de tão perto quanto desejado por um polinomial. Polinômios também são usados com freqüência para interpolar funções.

Quocientes de polinômios são chamados expressões racionais e funções que avaliam expressões racionais são chamados funções racionais. Funções racionais são as únicas funções que podem ser avaliados em um computador por uma seqüência fixa de instruções que envolvem operações de adição, multiplicação, divisão, que as operações em números de ponto flutuante são geralmente implementadas em hardware. Todas as outras funções que os computadores precisam de avaliar, como as funções trigonométricas , logaritmos e funções exponenciais , deve, então, ser calculado em software que podem usar aproximações a essas funções em determinados intervalos de funções racionais, e possivelmente iteração.

Calcular derivadas e integrais de polinômios é particularmente simples. Para o polinômio

a derivada em relação ax é

e a integral indefinida é

.

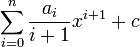Abstract álgebra

Em álgebra abstrata , deve-se tomar cuidado para distinguir entre polinômios e funções polinomiais. A f polinômio em uma indeterminado sobre um anel é definido como sendo uma expressão formal do formulário

onde 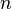é um número natural, os coeficientes são elementos de e X é considerado para ser um símbolo formal. Dois polinômios que compartilham o mesmo valor de 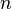são considerados iguais se e somente se as sequências dos seus coeficientes são iguais; além disso, qualquer polinômio é igual a qualquer polinômio com maior valor de 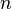obtido a partir dele, adicionando termos cujo coeficiente é zero. Polinômios em com coeficientes podem ser adicionados simplesmente adicionando coeficientes correspondentes (a regra para que prorroga por um acordo com coeficientes zero pode ser usado para fazer existir certeza tais coeficientes). Elas podem ser multiplicadas usando o lei distributiva e do Estado

para todos os elementos a, b do anel R e todos os números naturais K e L.

Pode-se então verificar que o conjunto de todos os polinômios com coeficientes no r se forma um anel de anel, o anel de polinômios mais de R, que é designado por R [X]. Se R é comutativo , então R [X] é um álgebra sobre R.

Pode-se pensar o anel R [X] como resultante de R adicionando um novo elemento para R X e apenas exigindo que comute X com todos os elementos do R. Para que R [X] para formar um anel, todas as combinações lineares de poderes de X têm de ser incluídos também. A formação do anel de polinômios, juntamente com a formação de anéis de fator de factoring fora ideais, são ferramentas importantes para a construção de novos anéis de outros conhecidos. Por exemplo, a construção de limpa campos finitos envolve o uso dessas operações, começando com o campo de inteiros módulo algum número primo como o anel de coeficiente R (ver aritmética modular ).

Se é comutativo , então pode-se associar a cada f polinômio em , Uma função polinomial com domínio e intervalo igual (De modo mais geral pode-se tomar domínio e intervalo a ser a mesma unital álgebra associativa sobre ). Obtém-se o valor desta função para um dado argumento r por toda a parte que substitui o símbolo X na expressão de f 's por r. Um dos motivos que algebristas distinguir entre polinômios e funções polinomiais é que mais de alguns anéis diferentes polinômios podem dar lugar à mesma função polinomial (veja Pequeno teorema de Fermat para um exemplo onde R é os inteiros módulo p). Este não é o caso quando são os números reais ou complexos e, portanto, muitos analistas muitas vezes não separar os dois conceitos. Uma razão ainda mais importante distinguir entre polinômios e funções polinomiais é que muitas operações sobre polinômios (como Divisão euclidiana) exige olhar para o que um polinômio é composto como uma expressão ao invés de avaliá-lo em algum valor constante para . E deve notar-se que, se não é comutativa, não existe (bem comportada) noção de função polinomial em tudo.

Divisibilidade

Em álgebra comutativa, um dos principais focos de estudo é a divisibilidade entre polinômios. Se o símbolo R representa um domínio e f e g integral são polinômios em R [X], diz-se que f divide g se existe um polinômio q em R [X] tal que f q = g. Em seguida, pode-se mostrar que "todos zero, dá origem a um factor linear", ou mais formalmente: se f é um polinómio em I [X] e r é um elemento de R tal que f (r) = 0, então o polinómio ( X - r) divide f. O inverso também é verdadeiro. O quociente pode ser calculado usando o Esquema de Horner.

Se F é uma campo e f e g são polinômios em F [X] com g ≠ 0, então existem polinômios q única e r na F [X] com

e de tal modo que o grau de r é menor do que o grau de g. O polinômios q e r são determinados exclusivamente por f e g. Isso é chamado de "a divisão com resto" ou " polinomial divisão longa "e mostra que o anel F [X] é um Domínio euclidiano.

Analogamente, "primos" polinomiais (mais corretamente, polinómios irredutíveis) podem ser definidos, que não pode ser fatorado para o produto de dois polinómios de menor grau. Não é fácil determinar se um determinado polinomial é irredutível. Pode-se começar, basta verificar se o polinômio tem fatores lineares. Então, pode-se verificar divisibilidade por alguns outros polinômios irredutíveis. Critério de Eisenstein também pode ser usada em alguns casos para determinar irredutibilidade.

Veja também: Máximo divisor comum de dois polinômios.

Classificações

A classificação mais importante dos polinómios baseia-se do número de variáveis distintas. Um polinômio em uma variável é chamado de um polinômio univariada, um polinômio em mais de uma variável é chamado de um polinômio multivariada. Estas noções se referem mais ao tipo de polinômios é geralmente um trabalho com que a polinômios individuais; por exemplo, quando se trabalha com um polinômios de uma variável não exclui polinômios constantes (que pode resultar, por exemplo, a partir da subtração de polinômios não constantes), embora a rigor polinômios constantes não contêm quaisquer variáveis em tudo. É possível classificar mais polinómios multivariada como bivariada, trivariado etc, de acordo com o número de variáveis, mas isso raramente é feito; é mais comum, por exemplo, dizer simplesmente "polinómios em x, y, e z". A (geralmente mulitvariate) polinomial é chamada homogénea de grau n se todos os seus termos têm grau n.

Polinômios de uma variável têm muitas propriedades que não são partilhadas por polinômios multivariados. Por exemplo, os termos de um polinômio univariada são completamente ordenados por seu grau, e é convencional para escrevê-los sempre em ordem decrescente de grau. Um polinômio univariada em x de grau n, em seguida, toma a forma geral

c onde _n, c _n-1, ..., c _2, c ₁ e c são constantes de _0, os coeficientes deste polinómio. Aqui, o termo c _n x ⁿ é chamado o termo de liderança e seu coeficiente c _n o coeficiente líder; se o coeficiente principal é 1, o polinômio univariada é chamado monic. Note-se que para além do líder coeficiente c _n (que deve ser diferente de zero ou então o polinómio não seria de grau n) a forma geral permite coeficientes para ser igual a zero; quando isso acontece, o termo correspondente é zero e pode ser removido a partir da soma sem alterar o polinómio. No entanto, é comum referir-se a c _i como o coeffient de x ^i, mesmo quando c _i passa a ser 0, de modo que x ⁱ realmente não ocorrer em qualquer prazo; por exemplo, pode-se falar da termo constante do polinômio, ou seja, c _0, mesmo se ele deve ser zero.

Polinômios pode igualmente ser classificadas pelo tipo de valores constantes permitida como coeficientes. Pode-se trabalhar com polinômios com coeficientes inteiros, racionais, reais ou complexos, polinômios e na álgebra abstrata com muitos outros tipos de coeficientes pode ser definida. Como para a classificação anterior, isto é sobre os coeficientes de um é geralmente trabalham com; por exemplo, quando se trabalha com polinómios com coeficientes complexos inclui um polinómios cujos coeficientes de acontecer a todos ser real, mesmo que tais polinómios também pode ser considerado como sendo um polinómios com coeficientes reais.

Polinómios podem ainda ser classificados pelo seu grau e / ou o número de termos diferentes de zero que contêm.

Polinômios classificadas por grau

Grau	Nome	Exemplo
	zero
	(Não-zero) constante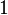
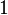	linear
	quadrático
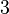	cúbico
	quartic ou biquadrática
	quintic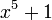
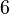	sêxtica ou Hexic
	séptico ou heptic
	octic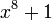
	nonic
	Decic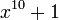

Os nomes para graus mais elevados do que 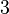são menos comuns. Os nomes para os graus pode ser aplicado para o polinómio ou para estes termos. Por exemplo, uma constante pode referir-se a um polinómio de grau zero ou para um termo grau zero.

O polinomial 0, o que pode ser considerado como não têm em termos de tudo, chama-se o polinómio de zero. Ao contrário de outros polinómios constantes, o seu grau não é zero. Pelo contrário, o grau do polinômio zero é ou deixou explicitamente indefinido, ou definido para ser negativo (ou -1 ou -∞) . A última convenção é importante para definir Divisão euclidiana de polinômios.

Polinômios classificadas por número de termos diferentes de zero

Quantidade de termos diferentes de zero	Nome	Exemplo
	de zero polinomial
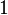	monômio
	binômio
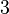	trinômio

A palavra monomial pode ser ambíguo, como também é muitas vezes utilizado para designar apenas um poder da variável, ou no produto caso multivariada de tais poderes, sem qualquer coeficiente. Dois ou mais termos que envolvem o mesmo monomial no último sentido, em outras palavras, que diferem apenas no valor dos seus coeficientes, são chamados de termos semelhantes; eles podem ser combinados em um único termo adicionando seus coeficientes; Se o termo resultante tem coeficiente de zero, ele pode ser removido completamente. A classificação acima de acordo com o número de termos que assume termos semelhantes foram combinados em primeiro lugar.

Extensões do conceito de um polinômio

Também se fala de polinômios em diversas variáveis, obtidos tomando o anel de polinômios de um anel de polinômios: R [X, Y] = (R [X]) [Y] = (R [Y]) [X]. Estes são de fundamental importância geometria algébrica que estuda as simultâneas de zero conjuntos de vários desses polinômios multivariados.

Polinômios são frequentemente utilizados para codificar a informação sobre algum outro objeto. O polinômio característico de um operador de matriz ou linear contém informações sobre o operador valores próprios . O polinomial mínima de um elemento algébrico registra a mais simples relação algébrica satisfeita por esse elemento.

Outros objetos relacionados estudadas em álgebra abstrata são série de potências formal, que são como polinômios, mas pode ter infinita grau, ea funções racionais, que são razões de polinômios.