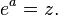Logaritmo
Sobre este escolas selecção Wikipedia
Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . SOS mães cada um cuidar de uma família de crianças apadrinhadas .
O logaritmo de um número é o expoente que por outro valor fixo, o de base, deve ser levantada para produzir esse número. Por exemplo, o logaritmo de base de 1000 a 10 é 3, porque 1000 é 10 à potência. 3: 1000 = 10 × 10 × 10 = 10 3 De modo mais geral, se x = b Y, então Y é o logaritmo de x para base b, e é escrita y = log b (x), de modo log 10 (1000) = 3.
O logaritmo de base b = 10, a é chamado logaritmo comum e tem muitas aplicações na ciência e engenharia. O logaritmo natural tem a constante e (≈ 2.718) como sua base; seu uso é difundido em matemática pura, especialmente cálculo . O logaritmo binário usa base b = 2 e é destaque em ciência da computação .
Logaritmos foram introduzidas por John Napier, no início do século 17 como um meio para simplificar os cálculos. Eles foram rapidamente adotados por navegadores, cientistas, engenheiros e outros para realizar cálculos mais facilmente, usando réguas de cálculo e tábuas de logaritmos. Etapas tediosas multiplicação multi-dígito pode ser substituído por tabela look-ups e adição simples devido ao fato - importante em seu próprio direito - que o logaritmo de um o produto é soma dos logaritmos dos factores:
A noção atual de logaritmos vem de Leonhard Euler , que lhes ligado à função exponencial no século 18.
Escalas logarítmicas reduzir as quantidades de grande alcance para escopos menores. Por exemplo, a decibéis é uma unidade logarítmica de quantificação rácios de pressão e voltagem de som. Em química, O pH é uma medida logarítmica para a acidez de um solução aquosa. Logaritmos são comuns em científicos fórmulas , e em medições da complexidade de algoritmos e de objectos geométricos chamado fractais . Eles descrevem intervalos musicais, aparecem em fórmulas contagem números primos , informar em alguns modelos psicofísica, e pode ajudar na contabilidade forense.
Da mesma maneira como o logaritmo inverte exponenciação , o logaritmo complexo é a função inversa da função exponencial aplicado a números complexos . O logaritmo discreto é uma outra variante; tem aplicações em criptografia de chave pública.
Motivação e definição
A idéia de logaritmos é reverter a operação de exponenciação , que está levantando um número a uma potência. Por exemplo, a terceira potência (ou cubo) é de 2 8, 8, porque é o produto de três factores de 2:
Daqui resulta que o logaritmo de 8 com respeito à base 2 é 3, de modo log 2 8 = 3.
Exponenciação
A terceira potência de algum número b é o produto de três factores de b. De modo mais geral, o aumento b para o poder n -ésimo, onde n é um número natural , é feito através da multiplicação n factores de b. O poder n -ésimo de b está escrito b n, de modo que
Exponentation pode ser alargado a b y, onde b é um número positivo e o expoente y é qualquer número real . Por exemplo, -1 b é a recíproco de b, isto é, 1 / b.
Definição
O logaritmo de um número x em relação à base de b é o expoente pelo qual b deve ser aumentado para se obter x. Em outras palavras, o logaritmo para a base de x b é a solução para a equação y
O logaritmo é denotado "log b (x)" (pronunciado como "o logaritmo para a base de x b" ou "o logaritmo de base-b x"). Na equação y = log b (x), o valor y é a resposta para a pergunta "Para que o poder deve ser levantada B, a fim de produzir x?". Para definir o logaritmo, a base b deve ser um número real positivo não é igual a 1 e x tem de ser um número positivo.
Exemplos
Por exemplo, log 2 (16) = 4, desde 2 de 4 = 2 × 2 × 2 × 2 = 16. Logaritmos também pode ser negativa:
desde
Um terceiro exemplo:. Log 10 (150) é de aproximadamente 2.176, que se situa entre 2 e 3, assim como 150 situa-se entre 10 100 e 2 = 10 3 = 1000 Finalmente, para qualquer base b, log b (b) = 1 e log b (1) = 0, uma vez que b 1 = b = 0 e b 1, respectivamente.
Identidades logarítmicas
Várias fórmulas importantes, às vezes chamado identidades logarítmicas ou leis de registro, logaritmos relacionar um com o outro.
Produto, quociente, poder e raiz
O logaritmo de um produto é a soma dos logaritmos dos números de serem multiplicados; o logaritmo da razão de dois números é a diferença entre os logaritmos. O logaritmo da potência p -ésimo de um número é p vezes o logaritmo do número si; o logaritmo de uma raiz de p-ésima é o logaritmo do número dividido por p. A tabela a seguir lista essas identidades com exemplos:
| Fórmula | Exemplo | |
|---|---|---|
| produto |  |  |
| quociente |  |  |
| poder |  | 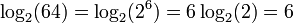 |
| raiz | ![\ Log_b \ sqrt [p] {x} = \ frac {\ log_b (x)} p \,](../../images/2455/245579.png) |  |
Alteração da base
O registo b logaritmo (x) pode ser calculado a partir dos logaritmos de x e b em relação à base de uma k arbitrário utilizando a seguinte fórmula:
Típico calculadoras científicas calcular os logaritmos de bases e 10 e. Logaritmos com respeito a qualquer base b pode ser determinada utilizando qualquer um destes dois logaritmos pela fórmula anterior:
Dado um número x e seu log logaritmo b (x) de uma base desconhecida b, a base é dada por:
Particular bases
Entre todas as opções para a base b, três são particularmente comuns. Estes são b = 10, b = e (o irracional constante matemática ≈ 2,71828), e b = 2. Em análise matemática , o logaritmo de base e é generalizada por causa de suas propriedades analíticas específicas explicadas abaixo. Por outro lado, o base-10 logaritmos são fáceis de usar para os cálculos manuais do decimal sistema de número:
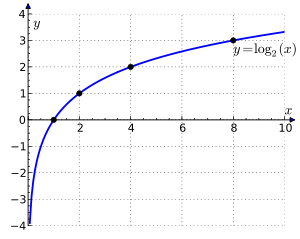
Assim, 10 log (x) está relacionada com o número de dígitos decimais de um número inteiro positivo x: o número de dígitos é o menor número inteiro estritamente maior do que log 10 (x). Por exemplo, log 10 (1430) é de aproximadamente 3.15. O próximo número inteiro é de 4, que é o número de dígitos de 1430. O logaritmo de base dois é usado em ciência da computação , onde o sistema binário é onipresente.
A tabela a seguir lista as notações comuns para logaritmos a estas bases e os campos onde são utilizados. Muitas disciplinas escrever log (x), em vez de log b (X), quando a base pretendida pode ser determinada a partir do contexto. O registo de notação b (x) também ocorre. Os "notação ISO" lista de coluna denominações sugeridas pelo International Organization for Standardization ( ISO 31-11).
| Base de b | Nome para log b (x) | Notação ISO | Outros notações | Usado em |
|---|---|---|---|---|
| 2 | logaritmo binário | lb (x) | ld (x), log (x), lg (x) | Ciência da Computação, teoria da informação, matemática |
| e | logaritmo natural | ln (x) | log (x) (Em matemática e muitas linguagens de programação ) | análise matemática, física, química, estatísticas , economia , e alguns campos da engenharia |
| 10 | logaritmo comum | lg (x) | log (x) (Em engenharia, biologia, astronomia), | vários engenharia campos (ver decibel e ver abaixo), logaritmo tabelas, handheld calculadoras, espectroscopia |
História
Antecessores
O Babilônios em algum momento de 2000-1600 BC pode ter inventado o algoritmo de multiplicação quadrado trimestre para multiplicar dois números utilizando apenas adição, subtração e uma tabela de quadrados. No entanto, não pode ser utilizado para a divisão sem uma tabela adicional de recíprocos. Grandes tabelas de quadrados trimestre foram usadas para simplificar a multiplicação precisa de um grande número de 1817 em diante, até este foi substituído pelo uso de computadores.
Michael Stifel publicado Arithmetica integra no Nuremberg em 1544, que contém uma tabela de números inteiros e potências de 2 que tem sido considerado uma versão inicial de uma tabela logarítmica.
Nos séculos 17 e início dos anos 16 um algoritmo chamado prosthaphaeresis foi usada para aproximar multiplicação e divisão. Este usou a identidade trigonométrica
ou semelhante para converter as multiplicações de adições e pesquisas de tabela. No entanto logaritmos são mais simples e requer menos trabalho. Pode ser mostrado usando números complexos que esta é basicamente a mesma técnica.
De Napier a Euler

O método de logaritmos foi proposto publicamente por John Napier, em 1614, em um livro intitulado Mirifici Logarithmorum Canonis Descriptio (descrição da regra Wonderful de Logaritmos). Joost Bürgi inventou logaritmos independentemente, mas publicado seis anos após Napier.
Johannes Kepler , que utilizou tábuas de logaritmos extensivamente para compilar seu Efemérides e, portanto, dedicou a Napier, comentou:
... O acento no cálculo levou Justus byrgius [Joost Bürgi] no caminho para estes muito logaritmos muitos anos antes de o sistema de Napier apareceram; mas ... em vez de criar o seu filho para o benefício público abandonou-a no nascimento.-Johannes Kepler, tabelas de Rudolphine (1627)
Por subtracções repetidas Napier calculada (1 - 10 -7) G para G que varia de 1 a 100. O resultado para L = 100 é aproximadamente 0,99999 = 1 - 10 -5. Napier, em seguida, calculados os produtos destes números com 10 7 (1 - 10 -5) G para G de 1 a 50, e de modo semelhante fez com 0,9998 ≈ (1 - 10 -5) 20 e 0,9 20 0,995 ≈. Estes cálculos, que ocuparam 20 anos, permitiu-lhe dar, para qualquer número N 5-10 milhões, o número L, que resolve a equação
Napier primeira chamada L "um número artificial", mas mais tarde introduziu a palavra "logaritmo" para significar um número que indica uma relação: λόγος ( logos) proporção que significa, e ἀριθμός (arithmos) significando número. Em notação moderna, a relação com logaritmos naturais é:
onde a aproximação muito estreita corresponde à observação de que
A invenção foi rápida e amplamente encontrou-se com aclamação. As obras de Bonaventura Cavalieri (Itália), Edmund Wingate (França), Xue Fengzuo (China), e Johannes Kepler 's chilias logarithmorum (Alemanha) ajudou a disseminar ainda mais o conceito.

Em 1647 Grégoire de Saint-Vincent relacionadas logaritmos para a quadratura da hipérbole, apontando que a área f (t), sob a hipérbole de x = 1 a x = t satisfaz
O logaritmo natural foi descrita pela primeira vez por Nicholas Mercator em seu trabalho Logarithmotechnia publicada em 1668, embora a matemática professor John Speidell já tinha compilado em 1619 uma mesa no logaritmo natural. Por volta de 1730, Leonhard Euler definida a função exponencial e logaritmo natural por
Euler também mostrou que as duas funções são inversas umas às outras.
Tábuas de logaritmos, réguas de cálculo e aplicações históricas

Ao simplificar cálculos difíceis, logaritmos contribuiu para o avanço da ciência, e especialmente da astronomia . Eles foram fundamentais para os avanços na agrimensura, navegação celestial, e outros domínios. Pierre-Simon Laplace chamados logaritmos
- "... [A] n artifício admirável que, ao reduzir a alguns dias o trabalho de muitos meses, duplica a vida do astrônomo, e poupa-lhe os erros e desgosto inseparáveis cálculos longos."
Uma ferramenta chave que permitiu a utilização prática dos logaritmos antes de calculadoras e computadores foi a tabela de logaritmos. O primeiro tal tabela foi compilado por Henry Briggs em 1617, imediatamente após a invenção de Napier. Posteriormente, as tabelas com o aumento da abrangência e precisão foram escritos. Estas tabelas listados os valores de log b (x) e b x para qualquer número x em um determinado intervalo, a uma certa precisão, durante um certo b base (normalmente b = 10). Por exemplo, Briggs 'primeira tabela continha os logaritmos comuns de todos os inteiros no intervalo 1-1000, com uma precisão de 8 dígitos. À medida que a função f (x) = b x é a função inversa do log b (x), que tem sido chamado o antilogaritmo. O produto e quociente de dois números c e d positivos foram rotineiramente calculada como a soma e diferença de seus logaritmos. O CD do produto ou quociente c / d veio procurar o antilogaritmo da soma ou a diferença, também através da mesma tabela:
e
Para cálculos manuais que exigem alguma precisão apreciável, realizando as pesquisas dos dois logaritmos, que calculam a soma ou diferença, e olhando para cima o antilogarithm é muito mais rápido do que realizar a multiplicação por métodos anteriores, como prosthaphaeresis, que se baseia em identidades trigonométricas. Cálculos de poderes e raízes são reduzidos a multiplicações ou divisões e look-ups por
e
Muitas tábuas de logaritmos dar logaritmos, fornecendo separadamente a característica e mantissa de x, ou seja, o parte inteira ea parte fracionária de log 10 (x). A característica de 10 · x é um mais a característica de x, e os seus significands são os mesmos. Isto alarga o âmbito das tabelas de logaritmos: dado um registo de perfil tabela 10 (x) para todos os números inteiros x variam entre 1 e 1000, o logaritmo de 3542 é aproximada pela
Outra aplicação importante foi o régua de cálculo, um par de escalas logarítmica divididos utilizados para o cálculo, conforme ilustrado aqui:

A escala logarítmica não deslizante, Regra de Gunter, foi inventado logo após a invenção de Napier. William Oughtred aumentada para criar o slide-regra um par de escalas logarítmicas móveis com respeito uma à outra. Os números são colocados em escalas de deslizamento em distâncias proporcionais às diferenças entre os seus logaritmos. Deslizando a escala superior adequadamente equivale a adição mecanicamente logaritmos. Por exemplo, adicionando a distância 1-2 na escala inferior à distância de 1 a 3 na escala superior produz um produto de 6, que é lido fora na parte inferior. A régua era uma ferramenta de cálculo essencial para cientistas e engenheiros até 1970, porque permite, em detrimento da precisão, a computação muito mais rápida do que as técnicas baseadas em tabelas.
Propriedades analíticas
Um estudo mais profundo dos logaritmos requer o conceito de uma função . Uma função é uma regra que, dado um número, produz outro número. Um exemplo é a produção de energia a -ésimo b x a partir de qualquer número real x, em que a base b é um número fixo de função. Esta função é escrita
Função logarítmica
Para justificar a definição de logaritmos, é necessário mostrar que a equação
x tem uma solução e que esta solução é único, desde que Y é positiva e que b é positivo e diferente de 1. A prova de que exige que o fato teorema do valor intermediário do elementar cálculo . Este teorema indica que um função contínua que produz dois valores m e n também produz qualquer valor que se situa entre m e n. Uma função é contínuo quando não "saltar", isto é, se o gráfico pode ser desenhado sem levantar a caneta.
Esta propriedade pode ser mostrado para manter para a função f (x) = b x. Porque f toma valores positivos arbitrariamente grandes e arbitrariamente pequenas, qualquer número y> 0 situa-se entre f (x 0) e f (x 1) para apropriado x 0 e X 1. Assim, o valor teorema intermédio assegura que a equação f (x) = y tem uma solução. Além disso, há apenas uma única solução para esta equação, porque a função F é estritamente crescente (por 1 b>), ou estritamente decrescente (para 0 <b <1).
A única solução x é o logaritmo de y a base b, b (y) log. A função que atribui a y seu logaritmo é chamado função logaritmo ou função logarítmica (ou apenas logaritmo).
Função inversa
A fórmula para o logaritmo de um poder diz, em particular, que, para qualquer número x,
Em prosa, tendo o poder de -th x b e, em seguida, o base-b logaritmo devolve x. Por outro lado, tendo em conta um número positivo para y, a fórmula
diz que primeiro ter tomado o logaritmo e depois exponencializando devolve y. Assim, as duas possíveis formas de combinar (ou compor ) logaritmos e exponenciação dar de volta o número original. Portanto, o logaritmo para a base b é a função inversa de f (x) = b x.
Funções inverso estão intimamente relacionados com as funções originais. Seu gráficos correspondem um ao outro sobre a troca do x - e os -coordena y (ou após reflexão na diagonal linha x = y), como mostrado à direita: um ponto (t, u = b t) no gráfico de rendimentos de f um ponto (u, t = u log b) no gráfico do logaritmo e vice-versa. Como conseqüência, b (x) log diverge para o infinito (se torna maior do que qualquer dado número) se x cresce para o infinito, desde que b é maior do que um. Nesse caso, b (x) é um log aumento da função. Para b <1, log b (x) tende a menos infinito em seu lugar. Quando x se aproxima de zero, log b (x) vai para o infinito para menos b> 1 (mais infinito para b <1, respectivamente).
Derivados e antiderivative
Propriedades analíticas de funções passam para suas inversas. Assim, como f (x) = b x é um processo contínuo e função diferenciável, então é log b (y). Grosso modo, uma função contínua é diferenciável se seu gráfico não tem "cantos" cortantes. Além disso, como o derivado de f (x) é avaliada como ln (b) b x pelas propriedades da função exponencial , a regra cadeia implica que o derivado de log b (X) é dado pela
Isto é, o inclinação da tangente do gráfico de tocar o logaritmo base-b no ponto (x, b log (x)) é igual a 1 / (x ln (b)). Em particular, o derivado de ln (x) é 1 / x, o que implica que o primitiva de 1 / x é ln (x) + C. O derivado com um argumento funcional generalizada de f (x) é
O quociente no lado da mão direita é chamado de derivada logarítmica de f. Calculando f (x), por meio do derivado de ln (f (x)) é conhecido como diferenciação logarítmica. O antiderivada do logaritmo natural ln (x) é:
Fórmulas relacionadas, tais como antiderivadas de logaritmos para outras bases podem ser derivados a partir desta equação usando a mudança de bases.
Representação integral do logaritmo natural
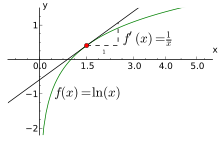
O logaritmo natural de t está de acordo com o integrante de um / dx x de 1 a t:
Em outras palavras, ln (T) é igual à área entre o eixo X e o gráfico da função 1 / x, variando de x = 1 a x = T (figura do lado direito). Esta é uma consequência do teorema fundamental do cálculo e do fato de que derivado de ln (x) é 1 / x. O lado direito desta equação pode servir como uma definição do logaritmo natural. Produto de energia e de logaritmos fórmulas pode ser derivado a partir desta definição. Por exemplo, o produto de fórmula ln (TU) = ln (t) + ln (L) é deduzido como:
A igualdade (1) divide o integral em duas partes, enquanto a igualdade (2) é uma mudança de variável (w = x / t). Na ilustração abaixo, o desdobramento corresponde a divisão da área em as partes de amarelo e azul. Redimensionando azul área da mão esquerda verticalmente pelo fator t e encolhê-lo pelo mesmo fator horizontalmente não muda o seu tamanho. Movendo-lo adequadamente, a área se encaixa o gráfico da função f (x) = 1 / x novamente. Portanto, a área azul lado esquerdo, que é o integral de f (x) a partir de t para tu é o mesmo que o integral de 1 a u. Isso justifica a igualdade (2) com uma prova mais geométrica.
A fórmula poder ln (t R) = r ln (T) podem ser derivados de um modo semelhante:
A segunda igualdade usa uma mudança de variáveis ( integração por substituição), w = x 1 / r.
A soma ao longo dos inversos dos números naturais,
chama-se a série harmônica. Ela está intimamente ligada ao logaritmo natural: como n tende a infinito , a diferença,
converge (ou seja, se aproxima arbitrariamente) para um número conhecido como o Constante de Euler-Mascheroni. Este ajudas relação ao analisar o desempenho de algoritmos como quicksort.
Há também uma outra representação integral do logaritmo que é útil em algumas situações.
Isto pode ser verificado por mostrando que tem o mesmo valor em x = 1, e o mesmo derivado.
Transcendência do logaritmo
O logaritmo é um exemplo de um função transcendental e de um ponto de vista teórico, o Gelfond-Schneider teorema afirma que logaritmos geralmente tomam valores "difíceis". A declaração formal se baseia na noção de números algébricos, que inclui todos os números racionais , mas também números, como o raiz quadrada de 2 ou
Os números complexos que não são algébrica são chamados transcendental; por exemplo, π e e são números tais. Quase todos os números complexos são transcendentais. Usando essas noções, as teorema Gelfond-Scheider que dados dois números algébricos a e b, log b (a) ou é um número transcendental ou um número racional p / q (no caso de um q = p b que, por isso, a e b estavam estreitamente relacionados para começar).
Cálculo
Logaritmos são fácil de calcular, em alguns casos, tal como log 10 (1000) = 3. Em geral, logaritmos pode ser calculada utilizando séries de potência ou o aritmética-média geométrica, ou ser recuperado a partir de um pré-calculado logaritmo tabela que fornece uma precisão fixa. método de Newton , um método iterativo para resolver equações aproximadamente, também pode ser usado para calcular o logaritmo, porque a sua função inversa, a função exponencial, pode ser calculado de forma eficiente. Usando tabelas look-up, CORDIC métodos semelhantes pode ser utilizado para calcular logaritmos se apenas as operações de adição e estão disponíveis bit turnos. Além disso, o logaritmo binário algoritmo calcula lb (x) recursivamente baseado em repetidas squarings de x, aproveitando-se da relação
Séries de potências
- Série de Taylor
Para qualquer número z real que satisfaz 0 <z <2, a seguinte fórmula contém:
Este é um atalho para dizer que ln (z) pode ser aproximada para um valor mais e mais precisos pelas seguintes expressões:
Por exemplo, com z = 1,5 a terceira aproximação produz 0,4167, que é de cerca de 0,011 superior a ln (1,5) = 0,405465. Este série aproxima ln (z) com precisão arbitrária, desde que o número de summands é grande o suficiente. No cálculo elementar, ln (z) é, por conseguinte, o limite desta série. É a série de Taylor do logaritmo natural em z = 1 A série de Taylor de ln z fornece uma aproximação particularmente útil para ln (1 + z) quando Z é pequena, |. z | << 1, desde então
Por exemplo, com z = 0,1 a aproximação de primeira ordem dá ln (1.1) ≈ 0,1, o que é menos do que 5% sobre o valor correcto 0,0953.
- Série mais eficiente
Outra série é baseado no área de função tangente hiperbólica:
para qualquer número real z> 0. Usando o Notação Sigma, este é também escrito como
Esta série pode ser derivada a partir da série de Taylor acima. Ela converge mais rapidamente do que a série de Taylor, especialmente se z é próximo de 1. Por exemplo, para z = 1,5, os três primeiros termos da série LN aproximada segunda (1.5) com um erro de cerca de 3 x 10 -6. A convergência rápida para z perto de 1 pode ser aproveitado da seguinte forma: dado um ln de baixa precisão aproximação y ≈ (z) e colocá-
o logaritmo de z é:
Quanto melhor for a aproximação inicial y é, o mais perto é um 1, então o seu logaritmo pode ser calculada de forma eficiente. A pode ser calculada utilizando a série exponencial , que converge rapidamente fornecida y não é muito grande. Calculando o logaritmo da maior z pode ser reduzida para valores menores de z escrevendo z = a b · 10, de modo que ln (z) = ln (a) + b · ln (10).
Um método intimamente relacionado pode ser utilizado para calcular o logaritmo dos números inteiros. Da série acima, segue-se que:
Se o logaritmo de um grande número inteiro n é conhecido, em seguida, esta série produz uma série rápida convergindo para o log (n + 1).
Aritmética-geométrica aproximação média
O aritmética-geométrica rendimentos médios aproximações de alta precisão do logaritmo natural. ln (x) é aproximada a uma precisão de 2 - p (ou p pedaços precisos) pela seguinte fórmula (devido a Carl Friedrich Gauss ):
Aqui M indica a média aritmética-geométrica. Ela é obtida através do cálculo repetidamente a média ( média aritmética ) e a raiz quadrada do produto de dois números ( média geométrica). Além disso, m é escolhido de tal modo que
Tanto a média aritmética-geométrica e as constantes π e ln (2) pode ser calculado com rapidamente convergente série.
Aplicações
Logaritmos têm muitas aplicações dentro e fora da matemática. Algumas dessas ocorrências estão relacionadas com a noção de invariância de escala. Por exemplo, cada uma das câmaras da concha de um Nautilus é uma cópia aproximada do próximo, escalonado por um fator constante. Isto dá origem a um espiral logarítmica. A lei de benford na distribuição de números iniciais também podem ser explicados pela invariância de escala. Logaritmos também estão ligados à auto-similaridade. Por exemplo, logaritmos aparecem na análise de algoritmos que resolvem um problema dividindo-a em dois problemas menores e semelhantes patching suas soluções. As dimensões de formas geométricas auto-semelhante, isto é, formas cujas partes se assemelham a imagem global também são baseados em logaritmos. Escalas logarítmicas são úteis para quantificar a mudança relativa de um valor em oposição à sua diferença absoluta. Além disso, porque a função logarítmica log (x) cresce muito lentamente para grandes x, escalas logarítmicas são usadas para comprimir dados científicos de grande escala. Logaritmos também ocorrer em numerosas fórmulas científicas, tais como a Equação do foguete Tsiolkovsky, o Equação Fenske, ou o Equação de Nernst.
Escala logarítmica
Quantidades científicos são muitas vezes expressos em logaritmos de outras quantidades, utilizando uma escala logarítmica. Por exemplo, a decibéis é uma unidade logarítmica de medição. Baseia-se o logaritmo comum de Rácios - 10 vezes o logaritmo comum de um relação de potência ou 20 vezes o logaritmo comum de um relação de tensão. Ele é utilizado para quantificar a perda de níveis de tensão na transmissão de sinais eléctricos, para descrever os níveis de energia de sons em acústica, eo absorvância de luz nas áreas de espectrometria e óptica . O relação sinal-para-ruído que descreve a quantidade de indesejada ruído em relação a um (significativa) sinal é também medida em decibéis. Na mesma linha, o pico de sinal-para-ruído é vulgarmente usado para avaliar a qualidade de som e métodos de compressão de imagens usando o logaritmo.
A força de um terremoto é medido por ter tomado o logaritmo comum da energia emitida pelo terremoto. Este é utilizado na escala de magnitude de momento ou no Escala Richter. Por exemplo, um terramoto 5.0 liberta 10 vezes e uma média de 6,0 liberta 100 vezes a energia de um 4.0. Outra escala logarítmica é magnitude aparente. Ele mede o brilho de estrelas logarítmica. Ainda um outro exemplo é pH em química ; pH é o negativo do logaritmo comum do actividade de iões hidrónio (a forma de hidrogênio íons H + levar em água). A atividade de íons hidrônio em água neutra é de 10 -7 mol·L -1, portanto, um pH de 7. O vinagre tem tipicamente um pH de cerca de 3. A diferença de 4 corresponde a uma proporção de 10 4 da actividade, isto é, actividade de iões hidrónio de vinagre é de cerca de 10 -3 mole · L -1.
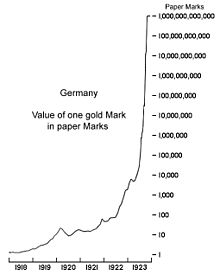
Semilog (log-lineares) gráficos utilizam o conceito escala logarítmica para visualização: um eixo, normalmente a uma vertical, é escalada de forma logarítmica. Por exemplo, o gráfico da direita comprime o aumento acentuado 1.000.000-1000000000000 para o mesmo espaço (no eixo vertical) como o aumento de 1-1 milhões. Nesses gráficos, funções exponenciais da forma f ( x ) = a · b x aparecem como linhas retas com inclinação igual ao logaritmo da b . Log-log gráficos escala logarítmica ambos os eixos, o que faz com que funções da forma f ( x ) = a · x k a ser descrito como linhas retas com inclinação igual ao expoente k . Isto é aplicado a visualizar e analisar as leis de potência.
Psicologia
Logaritmos ocorrer em várias leis descrevendo percepção humana: . A lei de Hick propõe uma relação logarítmica entre o momento em indivíduos levar para a escolha de uma alternativa e o número de escolhas que tem a lei de Fitts prevê que o tempo necessário para mover rapidamente a uma área-alvo é uma função logarítmica da distância e para o tamanho do alvo. Em psychophysics, a lei de Weber-Fechner propõe uma relação logarítmica entre estímulo e sensação como o real versus o peso percebido de um item uma pessoa está carregando. (Esta "lei", no entanto, é menos preciso do que os modelos mais recentes, como a lei de potência Stevens '.)
Estudos psicológicos descobriram que os indivíduos tendem matematicamente sofisticados para estimar quantidades logaritmicamente, isto é, eles posicionar um certo número de uma linha não marcada de acordo com o seu logaritmo, de modo que 10 é posicionado tão perto de 20 como é 100 a 200. O aumento da compreensão matemática para este desloca uma estimativa linear (posicionamento 100 10x tão longe).
Teoria da probabilidade e estatística
Logaritmos surgem na teoria das probabilidades : a lei dos grandes números determina que, para uma moeda honesta, como o número de moedas-lançamentos aumenta ao infinito, a proporção observada de cabeças se aproxima da metade . As flutuações dessa proporção cerca de metade são descritos pela lei do logaritmo iterado.
Logaritmos também ocorrem em distribuições log-normal. Quando o logaritmo de uma variável aleatória tem uma distribuição normal , a variável é dito ter uma distribuição log-normal. Distribuições de log-normal são encontradas em muitos campos, onde quer que uma variável é formada como o produto de muitas variáveis aleatórias positivos independentes, por exemplo, no estudo de turbulência.
Logaritmos são usados para máxima verossimilhança estimativa da paramétricos modelos estatísticos. Para um tal modelo, a função de probabilidade depende de, pelo menos, um parâmetro que deve ser estimado. Um máximo da função de probabilidade ocorre ao mesmo valor do parâmetro como-um máximo do logaritmo das probabilidades (o " probabilidade de log "), porque o logaritmo é uma função crescente. O log-verossimilhança é mais fácil para maximizar, especialmente para as probabilidades multiplicadas para variáveis aleatórias independentes.
A lei de benford descreve a ocorrência de dígitos em muitos conjuntos de dados, tais como a altura dos edifícios. De acordo com a lei de Benford, a probabilidade de que o primeiro decimal dígitos de um item de dados na amostra é d (1-9) é igual a log 10 ( d + 1) - log 10 ( d ), independentemente da unidade de medição. Assim, cerca de 30% dos dados pode ser esperado ter 1 como primeiro digito, 18% de partida com 2, etc Contas examinar os desvios da lei de Benford para detectar contabilidade fraudulenta.
Complexidade computacional
Análise de algoritmos é um ramo da ciência da computação que estuda o desempenho de algoritmos (programas de computador resolver um determinado problema). Logaritmos são valiosos para descrever algoritmos que dividem um problema em partes menores, e juntar-se as soluções dos subproblemas.
Por exemplo, para encontrar um número em uma lista ordenada, o algoritmo de busca binária verifica a entrada do meio e prossegue com a metade antes ou após a entrada do meio se o número ainda não foi encontrado. Este algoritmo requer, em média, log 2 ( N ) comparações, onde N é o comprimento da lista. Da mesma forma, o fundir algoritmo de ordenação classifica uma lista não ordenada, dividindo a lista em metades e classificar estes primeiros antes de fundir os resultados. Fundir algoritmos de classificação tipicamente exigem um tempo aproximadamente proporcional ao N · log ( N ) . A base do logaritmo não é especificado aqui, porque o resultado altera apenas por um factor constante quando outra base é utilizada. Um factor constante, é normalmente considerados na análise dos algoritmos de acordo com a norma modelo de custo uniforme.
A função f ( x ) é dito para crescer de forma logarítmica, se f ( x ) é (exactamente ou aproximadamente) proporcional ao logaritmo de x . (Descrições biológicas do organismo de crescimento, no entanto, usar este termo para uma função exponencial.) Por exemplo, qualquer número natural N podem ser representados em forma binária , em não mais do que log 2 ( N ) + 1 bocados. Por outras palavras, a quantidade de memória necessária para armazenar N cresce logaritmicamente com N .
Entropia e caos
A entropia é amplamente uma medida da desordem de algum sistema. Em termodinâmica estatística , a entropia S de algum sistema físico é definido como
A soma é sobre todos os possíveis estados i do sistema em causa, tal como as posições das partículas de gás em um recipiente. Além disso, P Eu é a probabilidade de que o estado i é atingido e k é a constante de Boltzmann. Da mesma forma, entropia na teoria da informação mede a quantidade de informação. Se um destinatário da mensagem pode esperar que qualquer uma das N possíveis mensagens com igual probabilidade, então a quantidade de informações fornecidas em qualquer uma dessas mensagens é quantificado como log 2 ( N ) bits.
Expoentes Lyapunov usar logaritmos para medir o grau de chaoticity de um sistema dinâmico. Por exemplo, para uma partícula movendo-se sobre uma mesa de bilhar oval, mesmo pequenas alterações das condições iniciais resultar em diferentes caminhos de partícula. Tais sistemas são caótica em uma forma determinista, porque pequenos erros de medição do estado inicial previsivelmente levar a muito diferentes estados finais. Pelo menos um expoente de Lyapunov de um sistema caótico deterministically é positivo.
Fractals
Logaritmos ocorrer em definições da dimensão de fractais . Fractais são objetos geométricos que são auto-semelhantes: pequenas peças reproduzir, pelo menos aproximadamente, toda a estrutura global. O Sierpinski triângulo (foto) pode ser coberta por três cópias de si mesmo, cada um com lados metade do comprimento original. Isso faz com que a dimensão de Hausdorff desta estrutura de registo (3) / log (2) ≈ 1,58 . Outra ideia-base logaritmo da dimensão é obtido pela contagem do número de caixas necessários para cobrir o fractal em questão.
Música
Logaritmos estão relacionados com tons musicais e intervalos. Em temperamento igual, o rácio de frequência depende apenas do intervalo entre dois tons, e não na frequência específica, ou tom, dos tons individuais. Por exemplo, a observe Um tem uma freqüência de 440 Hz e B-flat tem uma freqüência de 466 Hz. O intervalo entre A e B-flat é um semitom, como é aquela entre B-flat e B (freqüência de 493 Hz). Assim, os rácios de frequência concordam:
Portanto, logaritmos pode ser usado para descrever os intervalos: um intervalo é medido em meios tons, tendo a base de 2- 1/12 logaritmo do rácio de frequência, enquanto a base de 2- 1/1200 logaritmo da razão frequência expressa o intervalo de centavos, centésimos de semitom. O último é utilizado para a codificação mais fina, como for necessário para temperamento não iguais.
| Intervalo (Os dois tons são jogados ao mesmo tempo) | Jogo 1/12 tom | Jogo Semitone | Apenas major terceiro jogo | Terceiro jogo grande | Jogo Tritone | Jogo Octave |
| Frequência rácio r |  |  | 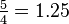 | ![\begin{align} 2^{\frac 4 {12}} & = \sqrt[3] 2 \\ & \approx 1.2599 \end{align}](../../images/2457/245704.png) |  | 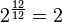 |
Número correspondente de semitons ![\log_{\sqrt[12] 2}(r) = 12 \log_2 (r)](../../images/2457/245707.png) |  |  | 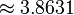 |  |  |  |
Número correspondente de centavos ![\log_{\sqrt[1200] 2}(r) = 1200 \log_2 (r)](../../images/2457/245712.png) |  |  |  |  |  | 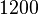 |
Teoria dos números
Logaritmos naturais estão intimamente ligados à contagem de números primos (2, 3, 5, 7, 11, ...), um tópico importante na teoria dos números . Para qualquer número inteiro x , a quantidade de números primos menos do que ou igual a x é denotado π ( x ). O número primo teorema afirma que π ( x ) é dado aproximadamente pela
no sentido de que a proporção de π ( x ) e que se aproxima de uma fracção quando x tende ao infinito. Como consequência, a probabilidade de que um número escolhido aleatoriamente entre 1 e x é primo é inversamente proporcional ao número de dígitos decimais de x . Uma muito melhor estimativa de π ( X ) é dado pela logaritmo integral deslocamento Li ( X ), definida pela
O Hipótese de Riemann, um dos mais antigos matemáticos abertasconjecturas, pode afirmar-se em termos de comparação π (x) e Li (x). O Erdös-Kac teorema descreve o número de distintosfatores primos também envolve o logaritmo natural.
O logaritmo de n fatorial , n ! 1 = 2 · · · ... n , é dada pela
Isto pode ser utilizado para se obter a fórmula de Stirling, uma aproximação de n ! para grande n .
Generalizações
Complexo logaritmo
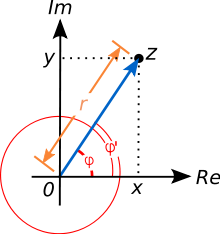
Osnúmeros complexos umaresolução da equação
são chamados logaritmos complexos . Aqui, z é um número complexo. Um número complexo é representado geralmente como z = x + iy , onde x e y são números reais e i é a unidade imaginária . Tal número pode ser visualizado por um ponto no plano complexo , como mostrado à direita. A forma polar codifica um complexo diferente de zero número Z pelo seu valor absoluto , isto é, a distância r à origem, e um ângulo entre o x e o eixo de linha que passa através da origem e z . Este ângulo é chamado o argumento de z . O valor absoluto r de Z é
O argumento não é unicamente especificada por z : tanto φ e φ '= φ + 2π são argumentos de z porque adicionar 2π radianos ou 360 graus para φ corresponde a "liquidação" em torno da origem-contra-relógio sábio por um turno. O número complexo resultante é novamente z , como ilustrado à direita. No entanto, exatamente um argumento φ satisfaz -π <φ e φ ≤ π . Ele é chamado o principal argumento , denotado Arg ( z ), com um capital A . (Uma normalização alternativa é 0 ≤ Arg ( Z ) <2π ).
Usandofunções trigonométricas seno ecosseno, ou ocomplexo exponencial, respectivamente,re φ são tais que as seguintes identidades segurar:
Isto implica que auma-ésimopodereé igual aZ, onde
φ é o principal argumento Arg ( Z ) e n é um número inteiro arbitrário. Qualquer um é chamado um logaritmo complexo de z . Há um número infinito delas, em contraste com o logaritmo verdadeiro exclusivamente definido. Se n = 0 , um é chamado o valor principal do logaritmo, denotado Log ( z ). O principal argumento de qualquer número real positivo x 0; daí Log ( x ) é um número real e é igual ao verdadeiro logaritmo (natural). No entanto, as fórmulas acima para logaritmos de produtos e poderes que não generalizar para o valor principal do logaritmo complexo.
A ilustração à direita mostra Log ( z ). A descontinuidade, isto é, o salto na matiz na parte negativa do x - ou eixo real, é causada pelo salto do principal argumento lá. Este lugar é chamado de corte ramo. Este comportamento só pode ser contornada por deixar cair a restrição de faixa em φ. Em seguida, o argumento de z e, conseqüentemente, seu logaritmo se tornar funções com valores múltiplos.
Inverses de outras funções exponenciais
Exponenciação ocorre em muitas áreas da matemática e da sua função inversa é muitas vezes referida como o logaritmo. Por exemplo, a logaritmo de uma matriz é a função (vários valores) inverso da matriz exponencial. Outro exemplo é a p -adic logaritmo, a função inversa da p -adic exponencial. Ambos são definidos através da série de Taylor análogo ao caso real. No contexto da geometria diferencial , o mapa exponencial mapeia o espaço tangente num ponto de um colector para um vizinhança desse ponto. Seu inverso também é chamado de logarítmica (ou registro) mapa.
No contexto da grupos finitos exponenciação é dada pela multiplicação do elemento repetidamente um grupob-se com. O logaritmo discreta é o número inteironresolvendo a equação
onde x é um elemento do grupo. Realizando a exponenciação pode ser feito de forma eficiente, mas o logaritmo discreto acredita-se ser muito difícil de calcular, em alguns grupos. Esta assimetria tem aplicações importantes em criptografia de chave pública, como por exemplo na troca de chaves Diffie-Hellman, uma rotina que permite trocas seguras de criptografia chaves ao longo de canais de informação inseguros. logaritmo da Zc está relacionado com o logaritmo discreto no grupo multiplicativo de não -zero elementos de um campo finito.
Outras funções inversas logaritmos-como incluir o logaritmo duplo ln (ln ( x )), o logaritmo-hiper-4 super- ou (uma ligeira variação dos quais é chamado logaritmo iterado em ciência da computação), a função Lambert W, e no logit . Eles são as funções inversas a função exponencial dupla, tetration, de F ( w ) = nós W , e da função logística, respectivamente.
Conceitos Relacionados
Do ponto de vista de matemática pura, a identidade log ( cd ) = log ( c ) + log ( d ) expressa um isomorfismo de grupos entre positivos reais sob multiplicação e reais sob disso. Funções logarítmicas são as únicas isomorfismos contínuas entre esses grupos. Por meio de que o isomorfismo, a medida de Haar ( medida de Lebesgue) dx sobre os reais corresponde ao Haar medir dx / x sobre os reais positivos. Em análise e complexas Geometria Algébrica, formas diferenciais da forma df / f são conhecidos como formulários com logarítmica pólos.
O polilogarítmo é a função definida por
Ela está relacionada com o logaritmo natural por Li 1 ( z ) = -ln (1 - z ) . Além disso, Li s (1) é igual à função zeta ζ (Riemann s ).
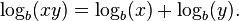

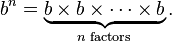







![\ Cos \, \ alpha \, \ cos \, \ beta = \ frac12 [\ cos (\ alpha + \ beta) + \ cos (\ alpha \ beta)]](../../images/2455/245585.png)

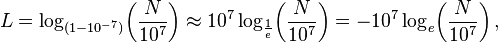




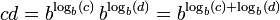
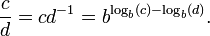
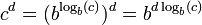
![\ Sqrt [d] {c} = c ^ {\ frac 1 d} = b ^ {\ frac {1} {d} \ log_b (c)}. \,](../../images/2456/245605.png)





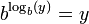







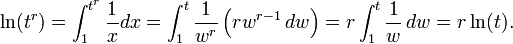



![\ Sqrt {-5+ \ sqrt [3] {13/03}}.](../../images/2456/245647.png)
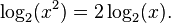



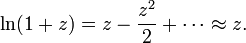
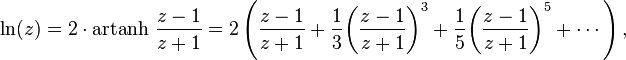












![\frac{466}{440} \approx \frac{493}{466} \approx 1.059 \approx \sqrt[12]2.](../../images/2457/245700.png)