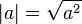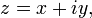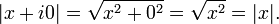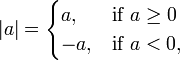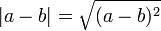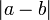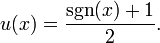Valor absoluto

Em matemática , o valor absoluto (ou módulo que é Latin para uma pequena medida) de um número real é o seu valor numérico sem consideração com seu sinal . Assim, por exemplo, 3 é o valor absoluto de ambos 3 e -3. Na programação de computadores , a função matemática usada para realizar este cálculo é geralmente dado o nome abs ().

Generalizações do valor absoluto para os números reais ocorrer em uma ampla variedade de configurações matemáticas. Por exemplo um valor absoluto também é definida para os números complexos , o quaternions, anéis ordenados, campos e espaços vetoriais . O valor absoluto está intimamente relacionado com as noções de magnitude, distância , e norma em vários contextos matemáticos e físicos.

O gráfico da função valor absoluto para números reais.

Números reais

Para qualquer número real de um valor absoluto ou módulo de uma é representada por | a | e é definido como

Como pode ser visto a partir da definição anterior, o valor absoluto de um ou é sempre positiva ou nula , mas nunca negativa .

De um ponto de vista geométrico, o valor absoluto de um número real é a distância ao longo da A linha número real de que o número de zero, e mais geralmente o valor absoluto da diferença de dois números reais, é a distância entre eles. Na verdade, a noção de um resumo função de distância em matemática pode ser visto como uma generalização do valor absoluto da diferença (ver "Distância" abaixo).

A proposição seguinte, dá uma identidade que às vezes é usado como uma alternativa (e equivalentes) definição do valor absoluto:

Proposição 1:

O valor absoluto tem as quatro propriedades fundamentais seguintes:

Proposição 2:

	Não-negatividade
	Positivo-definiteness
	Multiplicativeness
	Sub aditividade

Outras propriedades importantes do valor absoluto incluem:

Proposição 3:

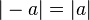
	Simetria
	Identidade dos indiscerníveis (equivalente a positive-definiteness)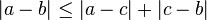
	Da desigualdade do triângulo (equivalente a sub aditividade)
	Preservação da divisão (equivalente a multiplicativeness)
	(Equivalente a sub aditividade)

Duas outras desigualdades úteis são os seguintes:

O acima são muitas vezes utilizados na resolução das desigualdades; por exemplo:

Os números complexos

O valor absoluto de um número complexo z é a distância r z para a origem. Veja-se também no quadro que Z e Z têm o mesmo valor absoluto.

Uma vez que os números complexos não são ordenada, a definição dada acima para o valor absoluto real pode não ser directamente generalizada para um número complexo. No entanto, a identidade dada na proposição 1:

pode ser visto como motivar a seguinte definição.

Para qualquer número complexo

em que x e y são números reais, o valor absoluto ou módulo de z é denotado | z | e é definido como

Segue-se que o valor absoluto de um número real x é igual ao seu valor absoluto considerado como uma série complexa, uma vez:

Semelhante à interpretação geométrica do valor absoluto de números reais, segue-se a partir do Teorema de Pitágoras que o valor absoluto de um número complexo é a distância no plano complexo do referido complexo a partir do número origem, e mais geralmente, que o valor absoluto da diferença de dois números complexos é igual à distância entre os dois números complexos.

As ações de valor absoluto complexos todas as propriedades do valor absoluto real dado nas Proposições 2 e 3 acima. Além disso, Se

e

é o conjugado complexo de z, em seguida, é facilmente visto que

e

com a última fórmula sendo o complexo análogo da Proposta 1 mencionado acima no caso real.

Uma vez que os reais positivos formam um subgrupo dos números complexos sob multiplicação, podemos pensar em valor absoluto como uma endomorphism do grupo multiplicativo de números complexos.

Funções de valor absoluto

A verdadeira função valor absoluto é contínua em todos os lugares. É diferenciável em todos os lugares, exceto para x = 0. É monotonamente decrescente no intervalo (-∞, 0] e aumenta monotonicamente no intervalo [0, ∞). Uma vez que um número real e o seu negativo têm o mesmo valor absoluto, é um mesmo funcionar, e não é, portanto, invertível.

O complexo função de valor absoluto é contínua em todos os lugares, mas (complexo) diferenciável nada (Uma maneira de ver isso é para mostrar que ele não obedecer à Cauchy-Riemann equações).

Ambas as funções são complexas e reais idempotent.

É um função não-linear.

Anéis de encomendadas

A definição do valor absoluto dado para números reais acima pode ser facilmente estendido para qualquer anel ordenada. Isto é, se a é um elemento de um anel R ordenada, em seguida, o valor absoluto de um, denotado por | a |, é definido como sendo:

onde - a é a inversa de um aditivo, e 0 é o aditivo elemento de identidade.

Distância

O valor absoluto está intimamente relacionado com a idéia de distância. Como observado acima, o valor absoluto de um número real ou complexa é a distância a partir desse número à origem, ao longo da linha de número real, para números reais, ou no plano complexo, para números complexos, e, mais geralmente, o valor absoluto da diferença de dois números reais ou complexos é a distância entre eles.

A norma Distância euclidiana entre dois pontos

e

em euclidiana -espaço n é definido como:

Isto pode ser visto como uma generalização de | a - b |, uma vez que se a e b são reais, em seguida, por uma proposição,

enquanto se

e

são números complexos, então

O exposto acima mostra que o "valor absoluto" distância para os números reais ou os números complexos, está de acordo com a distância euclidiana padrão herdam como resultado de considerá-los como um e espaços Euclidiana bidimensionais respectivamente.

As propriedades do valor absoluto da diferença de dois números reais ou complexos: não-negatividade, a identidade dos indiscerníveis, simetria e da desigualdade do triângulo dado em proposições 2 e 3 acima, pode ser vista a motivar a noção mais geral de um função de distância da seguinte forma:

A função real valorizado d em um conjunto X × X é chamado uma função de distância (ou uma métrica) em X, se preencher os quatro axiomas seguintes:

	Não-negatividade
	Identidade dos indiscerníveis
	Simetria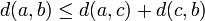
	Da desigualdade do triângulo

Derivativos

O derivado da função real valor absoluto é a função signum, sgn (x), que é definida como

para x ≠ 0. A função de valor absoluto não é diferenciável em x = 0. Quando a função de valor absoluto de um número real retorna um valor sem respeito a seu sinal, a função retorna signum sinal de um número sem respeito ao seu valor. Portanto x = SGN (x) abs (x). A função de signum é uma forma do Função de passo Heaviside utilizada no processamento de sinais, definido como:

em que o valor da função de Heaviside em zero é convencional. Portanto, para todos os pontos diferentes de zero no linha de número real,

A função de valor absoluto não tem concavidade em qualquer ponto, a função sinal é constante em todos os pontos. Por conseguinte, a segunda derivada de | x | em relação a x é zero em todos os lugares com excepção do zero, onde é indefinido.

A função de valor absoluto também é integrável. Sua antiderivada é

Campos

As propriedades fundamentais do valor absoluto de números reais dadas proposição 2 acima, pode ser utilizado para generalizar o conceito de valor absoluto a um campo arbitrária, como se segue.

Uma função v valor de real em um campo F é chamado de valor absoluto (também um módulo, magnitude, valor, ou uma avaliação), se preencher os quatro axiomas seguintes:

	Não-negatividade
	Positivo-definiteness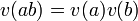
	Multiplicativeness
	Sub aditividade ou a desigualdade do triângulo

Sempre que 0 indica o aditivo elemento de identidade do F. Resulta positiva-definitude e multiplicativeness que v (1) = 1, onde 1 indica o elemento de identidade multiplicativo de F. Os valores absolutos reais e complexos acima definidos, são exemplos de valores absolutos de um campo arbitrária.

Se V é um valor absoluto de F, então a função d a F × F, definida por d (a, b) = v (a - b), é uma métrica e o seguinte são equivalentes:

• d satisfaz os desigualdade ultramétrica d (x, y) <d {max (x, z), d (y, z)}.

• é delimitada em R.

Um valor absoluto que satisfaz qualquer (daí todas) das condições acima é dito para ser não-Arquimedes, caso contrário, diz-se ser Arquimedes.

Espaços vectoriais

Mais uma vez as propriedades fundamentais do valor absoluto para os números reais podem ser utilizados, com uma ligeira modificação, para generalizar a noção de um espaço vetor arbitrário.

A função real valorizado || · || em um espaço vetorial V sobre um campo F, é chamado de um valor absoluto (ou mais geralmente uma norma), se preencher os seguintes axiomas:

Para todos os um em F, e v, u em V,

	Não-negatividade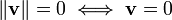
	Positivo-definiteness
	Homogeneidade positiva ou escalabilidade positivo
	Sub aditividade ou triângulo desigualdade

A norma de um vector também é chamado o seu comprimento ou magnitude.

No caso do espaço Euclidiano R ^n, a função definida pela

é uma norma chamada Norma euclidiana. Quando os números reais R são considerados como o one-dimensional vetor espaço ^R1 , o valor absoluto é um norma, e é a p -norm para qualquer p. De fato, o valor absoluto é a norma "apenas" em R ^1, no sentido de que, para cada norma || · || em R ^1, || x || = || 1 || · | x |. O valor absoluto complexo é um caso especial da norma em um espaço com produto interno. Ele é idêntico ao da norma euclidiana, se o plano complexo é identificado com o plano euclidiana ^R2.

Algoritmos

Na linguagem de programação C , o abs() , labs() , llabs() (em C99), fabs() , fabsf() , e fabsl() funções calcular o valor absoluto de um operando. Codificação a versão inteira da função é trivial, ignorando o caso limite em que o maior número negativo é de entrada:

 abs int (int i)
 {
     if (i <0)
         retornar -i;
     mais
         voltar i;
 }

O versões de ponto flutuante são mais complicados, como eles têm de lidar com códigos especiais para infinidades e não-um-número.

A função de valor absoluto em Fortran, Matlab, e GNU Octave é abs . Ele lida inteiro, verdadeiro, bem como números complexos.

Uso linguagem de montagem, é possível tomar o valor absoluto de um cadastre-se em apenas três instruções (exemplo mostrados para um registo de 32 bits em um arquitetura x86, Intel sintaxe):

 cdq
 xor eax, edx
 sub eax, edx

cdq estende o bit de sinal de eax para edx . Se eax é não-negativo, então edx torna-se zero, e os dois últimos instruções não têm nenhum efeito, deixando eax inalterada. Se eax é negativo, então edx se torna 0xFFFFFFFF, ou -1. As próximas duas instruções, em seguida, tornar-se um inversão de complemento de dois, dando o valor absoluto do valor negativo em eax .