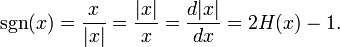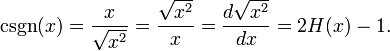Número negativo
Informações de fundo
Crianças SOS oferecem um download completo desta seleção para as escolas para uso em escolas intranets. Todas as crianças disponíveis para apadrinhamento de crianças de Crianças SOS são cuidadas em uma casa de família pela caridade. Leia mais ...
Um número negativo é um número que é menos do que de zero , tal como -3. Um número positivo é um número que é maior do que zero, tal como é em si 3. Zero positivos nem negativos. Os números não-negativos são os números reais que não são negativos (eles são positivos ou zero). Os números não-positivos são os números reais que não são positivas (eles são negativos ou zero).
No contexto de números complexos , implica real positivo, mas por motivos de clareza pode-se dizer "o número real positivo".
Os números negativos
Inteiros negativos pode ser considerado como uma extensão dos números naturais , de tal modo que a equação x - y = z tem uma solução significativa para todos os valores de x e y. Os outros conjuntos de números são, então, derivado como extensões progressivamente mais elaboradas e generalizações dos números inteiros.
Os números negativos são úteis para descrever os valores numa escala que vai abaixo de zero, tal como temperatura , e também em contabilidade, onde eles podem ser usados para representar dívidas. Em contabilidade, as dívidas são muitas vezes representado por números vermelhos, ou um número entre parênteses.
Números não-negativos
Um número é não-negativo se e somente se é maior que ou igual a zero, , isto é, positivo ou zero. Assim, os inteiros não negativos são todos os inteiros de zero em cima, e os reais não-negativos são todos os números reais de zero em cima.
Uma verdadeira matriz A é chamada não negativo se cada entrada de A é não-negativo.
Uma verdadeira matriz A é chamada totalmente não-negativo por teóricos da matriz ou totalmente positivo por cientistas da computação se o determinante de cada submatriz quadrada do A é não-negativo.
O negativo de um número é exclusivo
O negativo de um número é único, como é demonstrado pelo seguinte prova.
A prova é por contradição.
Seja x um número e deixe -x ser sua negativa. Deixar  . Deixar
. Deixar  ser outra negativa de x. Então deve ser verdade que
ser outra negativa de x. Então deve ser verdade que  . Por um axioma do sistema de número real
. Por um axioma do sistema de número real
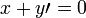 ,
,  .
.
Então,  . Usando a lei de cancelamento para além disso, vê-se que
. Usando a lei de cancelamento para além disso, vê-se que  , O que contradiz a nossa suposição. Portanto
, O que contradiz a nossa suposição. Portanto  é o mesmo número que
é o mesmo número que  e é o único negativa de x.
e é o único negativa de x.
Função Signum
É possível definir uma função sgn (x) sobre o número real, que é um dos números positivos, -1 para números negativos e 0 para zero (por vezes chamado de função signum):
Temos, então, (exceto para x = 0):
Onde | x | é o valor absoluto de x e h (x) é a Função de Heaviside. Ver também derivado .
Função Signum Complex
É possível definir uma função CSGN (x) sobre os números complexos, que é um dos números positivos, -1 para números negativos e 0 para zero (por vezes chamado de signum função complexa):
Onde o complexo desigualdade deve ser interpretado como se segue
Temos, então, (exceto para x = 0):
Aritmética envolvendo números assinados
Adição e subtração
Para fins de adição e subtração, pode-se pensar em números negativos como dívidas.
Adicionando um número negativo é o mesmo que subtraindo o número positivo correspondente:
- 5 + (-3) = 5 - 3 = 2
- (Se você tem US $ 5 e adquirir uma dívida de US $ 3, então você tem um patrimônio líquido de US $ 2)
- -2 + (-5) = -2 - 5 = -7
(A fim de evitar a confusão entre os conceitos de subtração e negação, muitas vezes o sinal negativo é escrita como um expoente:
- - 2 + - 5 = - 2-5 = - 7)
Subtrair um número positivo de um número positivo menor produz um resultado negativo:
- 4-6 = -2
- (Se você tiver US $ 4 e gastar US $ 6 então você tem uma dívida de US $ 2).
Subtraindo um número positivo a partir de qualquer número negativo produz um resultado negativo:
- -3 - 6 = -9
- (Se você tiver uma dívida de US $ 3 e gastar mais US $ 6, você tem uma dívida de US $ 9).
Subtraindo um negativo é equivalente a adicionar a correspondente positivo:
- 5 - (-2) = 5 + 2 = 7
- (Se você tiver um patrimônio líquido de US $ 5 e você se livrar de uma dívida de US $ 2, então o seu novo patrimônio líquido é de R $ 7).
Além disso:
- -8 - (-3) = -5
- (Se você tiver uma dívida de US $ 8 e se livrar de uma dívida de US $ 3, então você ainda tem uma dívida de US $ 5).
Multiplicação
Brahmagupta afirmou em Brahmasputhasiddhanta "tempos positivos positivo é vezes positivas e negativas negativo é positivo". Essa noção foi desafiado por Lazare Carnot (1753-1823). Ele perguntou como poderia o quadrado de um número menor ser maior do que o quadrado de um grande número. Em outras palavras praça de -3 é maior do que o quadrada de 2. No entanto -3 é menor do que 2. Essa objeção de Carnot a noção de Brahmagupta ficou incontestado durante um século. Grandes matemáticos como Euler, Laplace e Cauchy não foram capazes de dar uma resposta cabal. Hermann Hankel provou usando números complexos que Brahmagupta estava certo. . (Intuição Referência em Ciência e Matemática, Efrain Fischbein, Kluwer Academic Publishers, Springer, 1899) Multiplicação de um número negativo por um número positivo produz um resultado negativo: -2 x 3 = -6. A multiplicação de dois números negativos produz um resultado positivo: -4 × -3 = 12.
Uma maneira de entender isso é considerar a multiplicação por um número positivo como adição repetida. Pense de 3 x 2 como 3 grupos, com dois em cada grupo. Assim, 3 x 2 = 2 + 2 + 2 = 6 e assim naturalmente -2 × 3 = (-2) + (-2) + (-2) = -6.
A multiplicação por um número negativo pode ser considerada a adição repetida bem. Por exemplo, 3 × -2 pode ser pensada como a 3 grupos, com -2 em cada grupo. 3 × -2 = (-2) + (-2) + (-2) = -6. Observe que este mantém multiplicação comutativa : 3 × -2 = -2 x 3 = -6.
Aplicando a mesma interpretação de "multiplicação por um número negativo" para um valor que é também negativo, temos:
| -4 × -3 | = - (-4) - (-4) - (-4) |
| = 4 + 4 + 4 | |
| = 12 |
No entanto, do ponto de vista formal, multiplicação entre dois números negativos é recebida directamente por meio do distributividade da multiplicação sobre a adição:
| -1 × -1 | |
| = (-1) X (-1) + (-2) + 2 | |
| = (-1) X (-1) + (-1) 2 + 2 × | |
| = (-1) X (-1 + 2) + 2 | |
| = (-1) 1 + 2 × | |
| = (-1) + 2 | |
| = 1 |
Divisão
Divisão é semelhante à multiplicação. Brahmagupta indicado pela primeira vez que negativo dividido por ser positivo para negativo. Positivo negativo dividido por ser negativo. (Referência: Aritmética e mensuração de Brahmagupta por HT Colebrooke). Convenção de Brahmagupta sobreviveu até à data: se o dividendo e divisor têm sinais diferentes, então o resultado é negativo.
- 8 / -2 = -4
- -10/2 = -5
Se dividendo e divisor têm o mesmo sinal, o resultado é positivo, mesmo se ambos são negativos.
- -12 / -3 = 4
Construção formal de inteiros negativos e não negativos
De um modo semelhante ao número racional , que pode estender-se a números naturais N à inteiros Z definindo inteiros como um par ordenado de números naturais (a, b). Podemos estender adição e multiplicação destes pares com as seguintes regras:
- (A, b) + (c, d) = (a + c, b + d)
- (A, b) x (c, d) = (a x b x c + d, um x d + b x c)
Nós definimos uma relação de equivalência ~ sobre esses pares com a seguinte regra:
- (A, b) ~ (c, d) se e só se a + d = b + c.
Esta relação de equivalência é compatível com a adição e multiplicação definido acima, e que podem definir Z ser a quociente definido N ² / ~, ou seja, nós identificamos dois pares (a, b) e (c, d) se eles são equivalentes no sentido acima.
Nós também podemos definir uma ordem total sobre Z por escrito
- (A, b) ≤ (c, d) se e só se a + d ≤ b + c.
Isto irá levar a um aditivo zero da forma (a, a), um inverso de aditivo (a, b) da forma (b, a), uma unidade de forma multiplicativa (a + 1, a), e uma definição de subtracção
- (A, b) - (c, d) = (a + d, b + c).
Primeiro uso de números negativos
Durante muito tempo, as soluções para os problemas negativos eram considerados "falso", porque não podia ser encontrada no mundo real (no sentido em que não se pode, por exemplo, tem um número negativo de sementes). O conceito abstrato foi reconhecido mais cedo 100 aC - 50 aC A Obra chinesa, Nove Capítulos da Arte Matemática (Jiu-Zhang Suanshu), contém métodos para encontrar as áreas de figuras; vermelho contando varas foram usadas para denotar positivo coeficientes, barras pretas para negativo. Os chineses também foram capazes de resolver equações simultâneas envolvendo números negativos. O índio antigo Bakhshali Manuscrito, que foi escrito em algum momento entre 200 aC e 300 dC, realizada cálculos com números negativos, usando o "+" como um sinal negativo. Estas são as primeiras utilizações conhecidas de números negativos.
Em Egito helenístico, Diofante no século III a que se refere a uma equação que foi equivalente a 4 x 20 + = 0 (que tem uma solução negativa) em Aritmética, dizendo que a equação era absurda. Isto indica que o conceito de números negativos existia no Mediterrâneo antigo.
Durante o século VII dC, os números negativos foram usados na Índia para representar dívidas. O matemático indiano Brahmagupta , em Brahma-Sphuta-Siddhanta (escrito em 628 dC), discutiu o uso de números negativos para produzir a forma geral fórmula quadrática que permanece em uso hoje. Ele também encontrou soluções negativas de equações do segundo grau e deu regras relativas a operações com números negativos e zero, tais como "A dívida cortado do nada torna-se um crédito;. um crédito cortado do nada torna-se uma dívida" Ele chamou números positivos "fortunas, "zero" uma cifra ", e números negativos" dívidas ".
Durante o século VIII dC, o Mundo islâmico aprendeu sobre números negativos de árabes traduções de obras de Brahmagupta, e por AD 1000 matemáticos árabes estavam usando números negativos para dívidas.
No AD século XII na Índia, Bhaskara também deu raízes negativas para equações de segundo grau, mas rejeitou-los porque eles eram inadequados no contexto do problema. Ele afirmou que um valor negativo é ", neste caso, não deve ser tomada, porque é inadequada, as pessoas não aprovam raízes negativas."
Conhecimento de números negativos eventualmente chegou à Europa através latino traduções do árabe e obras indianas.
Europeias matemáticos, em sua maior parte, resistiu o conceito de números negativos até o século 17 , embora Fibonacci permitiu soluções negativas em problemas financeiros onde eles poderiam ser interpretadas como débitos (capítulo 13 Liber ábacos, AD 1202) e mais tarde como perdas (em Flos). Neste momento, os chineses foram indicando os números negativos pelo desenho de um curso diagonal através da mais à direita dígito diferente de zero.
No século 15, Nicolas Chuquet, um francês, utilizado como números negativos expoentes e se refere a eles como "números absurdos."
Em AD 1759, Francis Maseres, um matemático Inglês, escreveu que os números negativos "escurecer muito inteiras as doutrinas das equações e faça escuro das coisas que estão em sua natureza excessivamente óbvio e simples". Ele chegou à conclusão de que os números negativos não existia.
Os números negativos não foram bem compreendidos até os tempos modernos. Tão recentemente quanto o século 18 , a Swiss matemático Leonhard Euler acreditava que os números negativos foram maiores do que o infinito , um ponto de vista que foi compartilhado por John Wallis. Era prática comum naquela época para ignorar quaisquer resultados negativos derivados de equações, no pressuposto de que eles eram sem sentido. ( reformulado a partir de 4) O argumento de que os números negativos são maiores do que o infinito envolveu o quociente de 1 / x e considerando o que acontece quando x abordagens e atravessa o ponto x = 0 do lado positivo.