
Número inteiro
Sobre este escolas selecção Wikipedia
Crianças SOS, que corre cerca de 200 sos escolas no mundo em desenvolvimento, organizado esta selecção. Com SOS Children você pode escolher para patrocinar crianças em mais de cem países

Os inteiros (do latim inteiro, o que significa que com integridade intacta, inteiro) são o conjunto de números que consistem nos números naturais , incluindo 0 ( 0 , 1 , 2, 3, ...) e as suas negativos (0, -1, -2, -3, ...). São números que podem ser escritas sem um componente fracionário ou decimal, e cair dentro do conjunto {... -2, -1, 0, 1, 2, ...}. Por exemplo, 65, 7, e -756 são números inteiros; 1,6 e 1 ½ não são inteiros. Em outros termos, os números inteiros são os números que você pode contar com itens como maçãs ou os dedos, e seus negativos, incluindo 0.
Mais formalmente, os inteiros são a única domínio integral cujos elementos são positivos bem ordenado, e em que a ordem é preservada pela adição . Como os números naturais, os inteiros formar um conjunto infinito contável. O conjunto de todos os inteiros é muitas vezes indicado por um Z negrito (ou blackboard bold 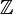 , Unicode U + 2124), que está para Zahlen ( alemão para números).
, Unicode U + 2124), que está para Zahlen ( alemão para números).
Em teoria dos números algébricos, estes números inteiros normalmente entendidos, embutido no campo de números racionais , são referidos como inteiros racionais para distingui-los da forma mais ampla definida inteiros algébricos.
Propriedades algébricas
Como os números naturais, Z é fechado sob a as operações de adição e multiplicação , isto é, a soma e produto de quaisquer dois inteiros é um número inteiro. No entanto, com a inclusão dos números naturais negativos, e, mais importante, de zero , Z (ao contrário dos números naturais) é também fechada sob subtração . Z não é fechado sob a operação de divisão , uma vez que o quociente de dois inteiros (por exemplo, 1 dividido por 2), não precisa ser um inteiro.
As listas a seguir algumas das propriedades básicas de adição e multiplicação por quaisquer inteiros a, b e c.
| adição | multiplicação | |
| Encerramento: | a + b é um número inteiro | um × b é um número inteiro |
| associatividade : | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| comutatividade : | a + b = b + a | a × b = b um × |
| existência de uma elemento de identidade: | a + 0 = um | um × 1 = um |
| existência de elementos inversos: | a + (- a) = 0 | |
| distributividade: | um × (b + c) = (a x b) + (c uma ×) | |
| Não divisores de zero: | Se a AB = 0, em seguida, a = 0 ou b = 0 (ou ambos) | |
Na linguagem da álgebra abstrata , os primeiros cinco propriedades listadas acima para adição dizer que Z sob disso é uma grupo abeliano. Como um grupo, com a adição, o símbolo Z representa um grupo cíclico , uma vez que cada número inteiro não nulo pode ser escrito como uma soma finita 1 + 1 + 1 ou ... (-1) + (-1) + ... + (-1) . Na verdade, com a adição de Z é o único grupo cíclico infinito, no sentido de que qualquer grupo cíclico é infinito isomorfo a Z.
As primeiras quatro propriedades listadas acima para a multiplicação dizer que Z sob a multiplicação é um monoid comutativa. No entanto, note que não cada inteiro tem um inverso multiplicativo; por exemplo, não há nenhum número inteiro tal que x = 2 x 1, porque o lado esquerdo é mesmo, enquanto que o lado direito é impar. Isso significa que sob a multiplicação Z não é um grupo.
Todas as regras da tabela propriedade acima, com exceção do último, tomados em conjunto dizer que Z juntamente com adição e multiplicação é um comutativa tocar com a unidade. Adicionando a última propriedade diz que o símbolo Z representa um domínio integral. Na verdade, Z fornece a motivação para a definição de uma tal estrutura.
A falta de inversos multiplicativos, que é equivalente ao facto de que Z não é fechado sob divisão, significa que Z não é um campo. O menor campo que contém os inteiros é o campo de números racionais . Este processo pode ser reproduzido para formar o campo de fracções de qualquer domínio integral.
Embora divisão comum não está definido em Z, ele não possuir uma propriedade importante chamada algoritmo de divisão: que é, tendo em conta dois inteiros a e b com b ≠ 0, existem inteiros exclusivos, q e r tais que a = q * b + r e 0 ≤ r <| B |, onde | b | denota o valor absoluto de b. O inteiro q é chamado o quociente e r é o chamado restante, resultante da divisão do a por b. Esta é a base para o Algoritmo de Euclides para calcular maiores divisores comuns .
Mais uma vez, na linguagem da álgebra abstrata, o acima diz que Z é um Domínio euclidiano. Isto implica que o símbolo Z representa um domínio de ideal principal e qualquer número inteiro positivo pode ser escrito como os produtos de números primos de uma maneira essencialmente única. Este é o teorema fundamental da aritmética .
Propriedades de ordem teórico-
O símbolo Z representa um totalmente conjunto ordenado sem superior ou limite inferior. A ordenação dos Z é dada por
- ... <-2 <-1 <0 <1 <2 <...
Um inteiro é positivo se for maior do que zero e negativo se é menor que zero. Zero é definida como nem negativo nem positivo.
A ordenação dos números inteiros é compatível com as operações algébricas no seguinte forma:
- se a <b e c <d, então a + c <b + d
- se a <b e 0 <c, então ac <bc. (A partir deste fato, pode-se mostrar que, se c <0, então ac> bc).
Daqui resulta que Z juntos com o ordenamento acima é um anel ordenada.
Construção
Os inteiros podem ser construídos a partir dos números naturais definindo classes de equivalência de pares de números naturais N × N sob uma relação de equivalência , "~", onde
precisamente quando
Tomando 0 para ser um número natural, os números naturais pode ser considerado como sendo números inteiros pela incorporação de mapas que n para [(N, 0)], onde [(a, b)] indica a classe de equivalência ter (, b a) como um membro.
A adição e a multiplicação de números inteiros são definidos como se segue:
É facilmente verificado que o resultado é independente da escolha dos representantes das classes de equivalência.
Tipicamente, [(a, b)] é denotada por
onde
Se os números naturais são identificados com os números inteiros correspondentes (usando a incorporação mencionada acima), esta convenção não cria nenhuma ambiguidade.
Esta notação recupera o familiar representação dos inteiros como {..., - 3, -2, -1,0,1,2,3, ...}.
Alguns exemplos são os seguintes:
Inteiros em computação
Um número inteiro (por vezes conhecido como "Int", do nome de um tipo de dados em linguagem de programação C ) é muitas vezes uma primitiva tipo de dados em linguagens de computador . No entanto, tipos de dados inteiros podem representar apenas um subconjunto de todos os inteiros, desde que os computadores são práticos de capacidade finita. Além disso, no comum representação complemento de dois, a definição inerente sinal distingue entre "negativo" e "não-negativo" em vez de "negativo, positivo, e 0". (É, no entanto, certamente possível para um computador para determinar se um valor de número inteiro é verdadeiramente positiva).
Representações de comprimento variável de números inteiros, como o bignums, pode armazenar qualquer número inteiro que se encaixa na memória do computador. Outros tipos de dados de números inteiros são implementados com um tamanho fixo, geralmente um número de bits que é uma potência de 2 (4, 8, 16, etc.) ou um número de dígitos decimais memorável (por exemplo, 9 ou 10).
Em contraste, os modelos teóricos de computadores digitais , tais como Máquinas de Turing, normalmente, não têm (finito mas apenas ilimitada) capacidade infinita.
Cardinalidade
O cardinalidade do conjunto de inteiros é igual a  . Isto é facilmente demonstrado pela construção de um bijection, isto é, uma função que é injective e surjective de
. Isto é facilmente demonstrado pela construção de um bijection, isto é, uma função que é injective e surjective de 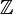 para
para  . Considere a função
. Considere a função
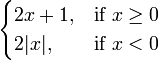 .
.
Se o domínio está restrita a 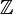 em seguida, cada membro da
em seguida, cada membro da 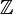 possui um e apenas um correspondente membro de
possui um e apenas um correspondente membro de  e pela definição de igualdade cardeal os dois conjuntos têm igual cardinalidade.
e pela definição de igualdade cardeal os dois conjuntos têm igual cardinalidade.


![[(A, b)] + [(c, d)]:. \ = [(A + c, b + d)],](../../images/94/9425.png)
![[(A, b)] \ cdot [(c, d)]:. = [(Ac + bd, ad + bc)] \,](../../images/94/9426.png)


![\ Begin {align} 0 & = [(0,0)] e = [(1,1)] & = \ cdots & & = [(k, k)] \\ 1 & = [(1,0)] & = [(2,1)] & = \ cdots & & = [(k + 1, k)] \\ -1 & = [(0,1)] & = [(1,2)] & = \ cdots & & = [(k, k + 1)] \\ 2 & = [(2,0)] & = [(3,1)] & = \ cdots & & = [(k + 2, k)] \\ -2 & = [(0,2)] e = [(1,3)] & = \ cdots & & = [(k, k + 2)] \ end {align}](../../images/94/9429.png)
