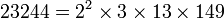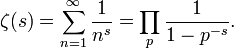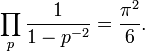Número primo

Baseada em conjuntos de divisibilidade de números inteiros Visão global Fatoração Integer Divisor Divisor unitário Função Divisor Fator primordial Teorema fundamental da aritmética Formas de fatoração Número primo Número Composite Número semiprime Número oblongo Número sphenic Número gratuito quadrado Número poderoso Poder perfeito Número de Aquiles Número suave Número regular Número bruto Número incomum Somas divisor constrangidos Número perfeito Número quase perfeito Número Quasiperfect Número perfeito Multiply Número Hemiperfect Número Hyperperfect Número Superperfect Número perfeito unitário Número semiperfect Número prático Com muitos divisores Abundante número Abundante número Primitive Número muito abundantes Número superabundante Número colossal abundante Número altamente composto Superior número altamente composto Número estranho Relacionado a sequências de alíquotas Número Untouchable Número amigável Número Sociável Número desposada Outros jogos Número deficiente Número amigável Número Solitary Número Sublime Número divisor Harmônica Número Frugal Número Equidigital Número extravagante

Em matemática , um número primo (ou um prime) é um número natural (maior do que um), que tem exatamente duas distintas número natural divisores : 1 e ele próprio. Uma infinidade de números primos existe, como demonstrado por Euclides torno 300 aC. Os primeiros trinta números primos são:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113
(Sequência A000040 em OEIS )

Veja a lista de números primos para uma lista mais longa. O número um é, por definição, não é um número primo; veja a discussão abaixo sob Primality de um .

A propriedade de ser um primo é chamado primality, ea palavra privilegiada também é usado como um adjetivo. Desde dois é o único mesmo número primo, o termo primo ímpar se refere a qualquer número primo maior que dois.

O estudo dos números primos é parte da teoria dos números , o ramo da matemática que engloba o estudo de números naturais. Os números primos têm sido objeto de intensa pesquisa, ainda algumas questões fundamentais, tais como a Hipótese de Riemann ea conjectura de Goldbach , ter sido resolvida por mais de um século. O problema de modelagem da distribuição de números primos é um assunto popular de investigação para os teóricos dos números: quando se olha para números individuais, os números primos parecem ser distribuídos aleatoriamente, mas a distribuição "global" de primos segue leis bem definidas.

A noção de número primo foi generalizada em diversos ramos da matemática.

• Em teoria dos anéis, um ramo da álgebra abstrata , o termo "elemento principal" tem um significado específico. Aqui, um não-zero, sem unidade de anel de um elemento é definido como sendo primo se sempre que divide um bc elementos para o anel B e C, em seguida divide um pelo menos um de b ou c. Com este significado, o inverso aditivo de qualquer número primo também é primo. Em outras palavras, quando se considera o conjunto de inteiros como um anel, -7 é um elemento primordial. Sem mais especificação, no entanto, "número primo" sempre significa um primo inteiro positivo. Entre os anéis de complexo inteiros algébricos, Eisenstein primos, e Primos Gaussianos pode também ser de interesse.
• Em teoria dos nós , um nó principal é um nó que não pode ser escrito como a soma de dois menor nó nós não triviais.

Histórico de números primos

O Crivo de Eratóstenes é um simples, antigo algoritmo para encontrar todos os números primos até um número inteiro especificado. É o antecessor do moderno Crivo de Atkins, que é mais rápido, mas mais complexo. A Peneira homônimo de Eratóstenes foi criado no Terceiro século aC por Eratóstenes, um grego antigo matemático .

Há indícios nos registros sobreviventes dos antigos egípcios que tinham algum conhecimento de números primos: o Expansões de fração egípcias no Papiro Rhind, por exemplo, têm formas bastante diferentes para primos e para compósitos. No entanto, os registros sobreviventes mais antigas do estudo explícita dos números primos vir dos gregos antigos . Elementos de Euclides (circa 300 aC) contêm teoremas importantes sobre números primos, incluindo a infinitude dos números primos eo teorema fundamental da aritmética . Euclides também mostrou como construir um número perfeito de um Primo de Mersenne. O Crivo de Eratóstenes, atribuído a Eratóstenes, é um método simples para calcular números primos, embora os grandes primos encontrados hoje com computadores não são gerados desta forma.

Após os gregos, pouco aconteceu com o estudo de números primos até o século 17. Em 1640 Pierre de Fermat declarou (sem prova) Pequeno teorema de Fermat (mais tarde provado por Leibnitz e Euler ). Um caso especial do teorema de Fermat pode ter sido conhecido muito antes pelos chineses. Fermat conjecturou que todos os números da forma ² 2 ⁿ + 1 são primos (eles são chamados Fermat números) e ele verificou este até n = 4. No entanto, o seguinte número de Fermat 2 ³² 1 é composta (um de seus fatores primos é 641), como Euler descobriu mais tarde, e na verdade não mais números de Fermat são conhecidos ser privilegiada. O monge francês Marin Mersenne olhou para números primos da forma 2 ^p - 1, com p um primo. Eles são chamados Primos de Mersenne em sua honra.

O trabalho de Euler na teoria dos números incluídos muitos resultados sobre números primos. Ele mostrou o série infinita _^1/2 + _^1/3 + _^1/5 + _^1/7 + _^1/11 + ... é divergente. Em 1747, ele mostrou que os números até perfeitos são precisamente os inteiros da forma 2 ^{p -1} (2 ^p -1), onde o segundo fator é primo Mersenne. Acredita-se não existem números perfeitos ímpares, mas ainda não há provas.

No início do século 19, Legendre e Gauss conjecturou que, como independente x tende ao infinito, o número de números primos até x é assintótica para x / log (x), onde log (x) é o logaritmo natural de x. Idéias de Riemann em 1859 seu papel na função zeta esboçado um programa que levaria a uma prova do teorema de número primo. Este esquema foi completado por Hadamard e de la Vallée Poussin, que se mostrou independentemente teorema do número primo em 1896.

Provando um número é primo não for feito (para grandes números) pela divisão de julgamento. Muitos matemáticos têm trabalhado em testes de primalidade para grandes números, muitas vezes restritos a formas numéricas específicas. Isso inclui O teste de Pépin para números de Fermat (1877), Teorema de PROTH (cerca de 1878), o Teste de Lucas-Lehmer para números Mersenne originado (1856), e o generalizada Teste de Lucas-Lehmer. Algoritmos mais recentes como APRT-CL, ECPP e AKS trabalhar em números arbitrários, mas permanecem muito mais lento.

Por um longo tempo, números primos foram pensados como não tendo qualquer possibilidade de aplicação fora do matemática pura; isso mudou na década de 1970, quando os conceitos de criptografia de chave pública foram inventadas, em que números primos formou a base dos primeiros algoritmos, tais como o Algoritmo RSA cryptosystem.

Desde 1951, todas as maiores números primos conhecidos foram encontrados por computadores . A busca de números primos cada vez maiores tem gerado interesse fora dos círculos matemáticos. O Grande Mersenne Prime Search and Internet outra projetos de computação distribuída para encontrar números primos grandes tornaram-se populares nos últimos dez a quinze anos, enquanto os matemáticos continuam a lutar com a teoria dos números primos.

Primality de um

Até o século 19, a maioria dos matemáticos considerado o número 1 um primo, e ainda há um grande corpo de trabalho matemático que é válido, apesar de rotulagem 1 a prima, tais como o trabalho de Stern e Zeisel. Lista de números primos até 10006721 de Derrick Norman Lehmer, reimpresso tão tarde quanto 1956 ,, começou com 1 como seu primeiro prime. Henri Lebesgue é dito ser o último matemático profissional para chamar um primo. A mudança no rótulo ocorreu para que o teorema fundamental da aritmética , como afirmou, é válido, ou seja, "cada número tem uma fatoração única em números primos"

Divisores primos

Ilustração que mostra que 11 é um número primo, enquanto 12 não é.

O teorema fundamental da aritmética afirma que cada número inteiro positivo maior que 1 pode ser escrito como um produto de um ou mais primos de uma maneira que é original exceto, possivelmente, para o fim dos principais fatores . O mesmo fator primordial pode ocorrer várias vezes. Primes podem assim ser considerados os "blocos de construção básicos" dos números naturais. Por exemplo, podemos escrever

e qualquer outro factorization de 23244 como o produto de números primos serão idênticos excepto para a ordem dos factores. Há muitos algoritmos de fatoração em primos para fazer isso na prática, para números maiores.

A importância deste teorema é uma das razões para a exclusão de um a partir do conjunto de números primos. Se 1 foram admitidos como um nobre, a indicação precisa do teorema exigiria qualificações adicionais.

Propriedades dos números primos

• Quando escrito em base 10 , todos os números primos, exceto 2 e 5 fim em 1, 3, 7 ou 9. (Números terminados em 0, 2, 4, 6 ou 8 representam múltiplos de 2 e números que terminam em 0 ou 5 representam múltiplos de 5.)

• Se p é um número primo p divide e um produto ab de inteiros, então p divide a ou p divide b. Essa proposição foi provado por Euclides e é conhecido como Lema de Euclides. Ele é usado em algumas provas da singularidade de fatorações primos.

• O anel Z / n Z (ver aritmética modular ) é uma campo se e somente se n é primo. Dito de outra forma: n é primo se, e somente se φ (n) = n - 1.

• Se p é primo e a é um número inteiro, então um ^p - a é divisível por p ( Pequeno teorema de Fermat).

• Se p é um número primo diferente de 2 e 5, ¹ / _p é sempre um decimal periódico, cujo período é p - 1 ou um divisor de p - 1. Isto pode ser deduzida directamente a partir de Pequeno teorema de Fermat. ¹ / _p expresso igualmente em q base (exceto base 10) tem efeito semelhante, desde que p não é um fator primordial de q. O artigo sobre decimais recorrentes mostra algumas das propriedades interessantes.

• Um número inteiro p> 1 é primo se, e somente se o fatorial (p - 1)! + 1 é divisível por p ( Teorema de Wilson). Por outro lado, um número inteiro n> 4 é composta, se e somente se (n - 1)! é divisível por n.

• Se n é um inteiro positivo maior que 1, então existe sempre um número primo com n p <p <2 N ( Postulado de Bertrand).

• Adicionando os recíprocos de todos os números primos juntos resulta em um divergente série infinita ( prova). Mais precisamente, se S (x) representa a soma de todos os recíprocos de números primos p com p ≤ x, então S (x) = x + LN LN O (1) para x → ∞.

• Em cada uma progressão aritmética, um q +, a + 2 q, a + 3 q, ... onde os inteiros A e Q são positivos coprime, existem infinitos números primos ( Teorema de Dirichlet sobre progressões aritméticas).

• O característico de cada campo é zero ou um número primo.

• Se L é um número finito grupo e p ⁿ é o maior poder do primo p que divide a ordem de G, então G tem um subgrupo de ordem p ^n. ( Teoremas de Sylow.)

• Se L é um grupo finito e p é um número primo que divide a ordem de G, então G contém um elemento de ordem p. ( Cauchy Teorema)

• O teorema de número primo diz que a proporção dos números primos menos do que x é assimptótica para ^um / _{x ln} (em outras palavras, quando x fica muito grande, a probabilidade de que um número menor que x é primo é inversamente proporcional ao número de dígitos x ).

• O Copeland-Erdős constante 0,235711131719232931374143 ..., obtido concatenando os números primos em base dez , é conhecido por ser um número irracional .

• O valor do Função zeta de Riemann em cada ponto no plano complexo é dado como uma continuação meromorfa de uma função, definida por um produto sobre o conjunto de todos os números primos para Re (s)> 1:

Avaliando essa identidade em diferentes inteiros fornece um número infinito de produtos ao longo dos primos cujos valores podem ser calculados, sendo os dois primeiros

• Se p> 1, o polinômio é irredutível sobre Z / p Z se e somente se p é primo.

Classificação dos números primos

Duas formas de classificação de números primos, classe e classe n + n -, foram estudados por Paul Erdős e John Selfridge.

Determinar a classe n + de um número primo p envolve olhar para o maior fator primordial de p + 1. Se essa maior fator primordial é 2 ou 3, então p é de classe 1+. Mas se essa maior fator primordial é outro q primo, então a classe de n + p é um a mais que a classe n + de q. Sequências A005105 através Classe A005108 lista 1+ através de números primos 4+ classe.

A classe n - é quase o mesmo que classe n +, exceto que a fatoração de p - 1 é olhado em seu lugar.

O número de números primos

Há infinitos números primos

A mais antiga prova conhecida para a afirmação de que existem infinitamente muitos números primos é dado pelo matemático grego Euclid em seus elementos (Livro IX, Proposição 20). Euclides afirma o resultado como "há mais de um determinado número [finito] dos números primos", e sua prova é essencialmente o seguinte:

Considere qualquer conjunto finito de números primos. Multiplique todos eles juntos e adicionar um (ver Número Euclid). O número resultante não é divisível por qualquer um dos números primos no conjunto finito que considerado, porque dividindo por qualquer destes daria um resto de um. Porque todos os números não primos pode ser decomposto em um produto de números primos subjacentes, em seguida, esse número resultante é primo em si, ou se houver um número primo números primos ou qual o número resultante poderia ser decomposta em mas não estão no conjunto finito inicial dos números primos. De qualquer forma, há pelo menos mais um nobre que não estava no conjunto finito que começou com. Este argumento aplica-se não importa o conjunto finito que começou com. Portanto, há mais primos do que qualquer número finito dado.

Este argumento anterior explica por que o produto P de um número finito de primos mais 1 deve ser divisível por algum nobre não entre aquelas número finito de números primos (possivelmente si).

A prova é por vezes formulada de uma forma que leva o aluno a concluir que P + 1 em si deve ser privilegiada, e acho que a prova de Euclides diz que o produto injetar mais 1 é sempre primordial. O exemplo simples de (2 · · 3 5 7 · · · 11 13) + 1 = 30.031 = 59 · 509 (ambos os primos) mostra que isto não é o caso. Na verdade, qualquer conjunto de números primos que não incluem 2 terá um produto ímpar. Adicionando 1 para este produto produzirá sempre um número par, que vai ser divisível por 2 (e, portanto, não ser primo).

Outros matemáticos têm dado outras provas. Um deles (devido a Euler ) mostra que a soma de todos os recíprocos de números primos diverge. Outro com base na prova Números de Fermat foi dada pelo Goldbach. Kummer de é particularmente elegante e Harry Furstenberg fornece um usando topologia geral.

Contar o número de números primos abaixo de um determinado número

Mesmo que o número total de números primos é infinito, ainda se podia pedir "Aproximadamente, quantas primos estão lá abaixo 100.000?", Ou "Qual a probabilidade de um número de 20 dígitos aleatórios para ser nobre?".

O função principal de contagem π (x) é definido como o número de números primos até x. Não são conhecidos algoritmos para calcular os valores exactos de π (x) mais rapidamente do que seria possível calcular-se a cada primo x. Valores tão grandes quanto π (10 ²⁰⁾ pode ser calculado com rapidez e precisão com computadores modernos. Assim, por exemplo, π (100,000) = 9592, e π (10 ²⁰⁾ = 2.220.819.602.560.918.840.

Para valores maiores de x, fora do alcance de equipamentos modernos, a teorema de número primo fornece uma boa estimativa: π (x) é de aproximadamente x / ln (x). Mesmo melhores estimativas são conhecidos.

Localização dos números primos

Encontrar números primos

A antiga Crivo de Eratóstenes é uma maneira simples para calcular todos os números primos até um determinado limite, por fazer uma lista de todos os inteiros e repetidamente eliminar múltiplos de já encontrou primos. O moderno Crivo de Atkin é mais complicado, mas mais rápido quando devidamente otimizado.

Na prática, muitas vezes quer verificar se um determinado número é primo, em vez de gerar uma lista de números primos. Além disso, é muitas vezes satisfatória para saber a resposta com uma alta probabilidade . É possível verificar rapidamente se um determinado número grande (digamos, até alguns milhares de dígitos) é primo usando probabilística testes de primalidade. Estes geralmente escolher um número aleatório chamado de "testemunha" e verifique alguma fórmula envolvendo a testemunha eo potencial privilegiada N. Depois de várias iterações, declaram N a ser "definitivamente composto" ou "provavelmente primo". Alguns destes testes não são perfeitos: pode haver alguns números compostos, chamados pseudoprimes para o respectivo teste, que será declarado "provavelmente primo" não importa o que testemunha é escolhido. No entanto, os testes probabilísticos mais populares não sofrem deste problema.

Um método para determinar se um número é primo é dividir por todos os primos menos do que ou igual à raiz quadrada do número que. Se qualquer das divisões sair como um número inteiro, então o número original não é primo. Caso contrário, ele é primo. Um não precisa realmente calcular a raiz quadrada; uma vez que se vê que o quociente é menos do que o divisor, pode-se parar. Isto é conhecido como a divisão de teste; é o teste de primalidade simples e rapidamente torna-se impraticável para testar grandes inteiros porque o número de possíveis fatores cresce exponencialmente à medida que o número de dígitos nos aumentos de número-a-ser-testadas.

Testes de primalidade

A algoritmo de teste de primalidade é um algoritmo que testa uma série de primalidade, ou seja, se o número é um número primo.

• Teste de primalidade AKS
• Teste de primalidade de Fermat
• Teste de Lucas-Lehmer
• Teste de primalidade Solovay-Strassen
• Teste de primalidade Miller-Rabin
• Curva elíptica primality prova

A provável primo é um número inteiro que, em virtude de ter passado um determinado teste, é considerado provavelmente primo. Prováveis primos que são na verdade composta (tais como Números de Carmichael) são chamados pseudoprimes.

Em 2002, cientistas indianos em IIT Kanpur descoberto um novo algoritmo determinista conhecido como AKS algoritmo. A quantidade de tempo que leva este algoritmo para verificar se um número N é primo depende de um função polinomial de o número de dígitos de N (ou seja, do logaritmo de N).

Fórmulas produzindo números primos

Não se conhece fórmula para primos que é mais eficiente em encontrar números primos do que os métodos mencionados acima em "Encontrar números primos".

Há um conjunto de Equações diofantinas em 9 variáveis e um parâmetro com a seguinte propriedade: o parâmetro é primo se, e somente se o sistema de equações resultante tem uma solução sobre os números naturais. Isto pode ser utilizado para obter uma única fórmula, com a propriedade de que todos os seus valores positivos são primos.

Não há polinomial , mesmo em diversas variáveis, que leva apenas valores primos. Por exemplo, o polinómio curioso em uma variável f (n) = N ² - N + 41 gera números primos para n = 0, ..., 40,43 mas f (41) e f (42) são compósito. No entanto, existem polinômios em diversas variáveis, cujos valores positivos como as variáveis tomar todos os valores inteiros positivos são exatamente os números primos.

Outra fórmula é baseada na teorema de Wilson mencionado acima, e gera o número dois muitas vezes e todos os outros primos exatamente uma vez. Há outras fórmulas semelhantes que também produzem primos.

Tipos especiais de números primos de fórmulas para primes

Um primo p é chamado primorial ou prime-factorial se ele tem a forma p = n # ± 1 para um número n, onde n # é o produto 2 · 3 · 5 · 7 · 11 · ... de todos os números primos ≤ n. A principal é chamado fatorial se ele é da forma ! n ± 1. Os primeiros números primos fatoriais são:

n! - 1 é primordial para n = 3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, 324, ... (sequência A002982 em OEIS )

n! + 1 é primordial para n = 0, 1, 2, 3, 11, 27, 37, 41, 73, 77, 116, 154, 320, ... (sequência A002981 em OEIS )

O maior primo conhecido é primorial Π (392.113) + 1, encontrado por Heuer em 2001. A maior primo conhecido é fatorial 34790! - 1, encontrado por Marchal, Carmody e Kuosa em 2002. Não se sabe se existem infinitos números primos primorial ou fatoriais.

Primes da forma 2 ^p - 1, em que p é um número primo, são conhecidos como Primos de Mersenne, enquanto que números primos da forma são conhecidos como Fermat primos. Prime números p onde dois p + 1 também é primo são conhecidos como Sophie Germain primos. A lista a seguir é de outros tipos especiais de números primos que vêm de fórmulas:

Alguns números primos são classificados de acordo com as propriedades de seus dígitos em decimal ou outras bases. Por exemplo, números cujos algarismos formar um sequência palindrómica são chamados palindr�icas primos, e um número primo é chamado de privilegiada truncatable se eliminando sucessivamente o primeiro dígito no os rendimentos direito apenas novos números primos esquerda ou.

• Para obter uma lista de classes especiais de números primos ver Lista de números primos

A distribuição dos números primos

A distribuição de todos os números primos no intervalo de 1 a 76.800, a partir da esquerda para a direita e de cima para baixo, em que cada pixel representa um número. Preto pixels significa que número é primo e branco significa que não é primo.

O problema de modelagem da distribuição de números primos é um assunto popular de investigação para os teóricos dos números. Os números primos são distribuídos entre os números naturais em uma maneira (até agora) imprevisível, mas não parecem ser leis que regem seu comportamento. Leonhard Euler comentou

Os matemáticos têm tentado, em vão, o dia de hoje para descobrir um pouco de ordem na seqüência de números primos, e nós temos razão para acreditar que ele é um mistério em que a mente nunca irá penetrar. (Havil 2003, p. 163)

Paul Erdős disse

Deus não joga dados com o universo, mas algo estranho está acontecendo com os números primos. [Referindo-se a Albert Einstein famoso crença de que "Deus não joga dados com o universo."]

Em uma palestra 1975, Don Zagier comentou

Há dois fatos sobre a distribuição dos números primos de que eu espero convencê-lo tão esmagadoramente que eles serão permanentemente gravado em seus corações. A primeira é que, apesar de sua definição simples e papel como os blocos de construção dos números naturais, os números primos crescem como ervas daninhas entre os números naturais, parecendo obedecer a nenhuma outra lei que não a do acaso, e ninguém pode prever onde o próximo brotarão. O segundo fato é ainda mais surpreendente, pois ele afirma exatamente o oposto: que os números primos exibem regularidade impressionante, que existem leis que regem seu comportamento, e que obedecer a essas leis com precisão quase militar.

(Havil 2003, p. 171)

Imagem adicional 2310 colunas está ligada aqui, preservando múltiplos de 2,3,5,7,11 na respectivas colunas.

Lacunas entre primos

Seja p _n denota o n-ésimo número primo (isto é, p = ₁ 2, p = _2, 3, etc.). A diferença entre o g _n consecutivo primos p _n e p _{n + 1} é a diferença entre eles, isto é,

g _n = p _{n + 1} - p _n.

Temos ₁ g = 3-2 = 1, ₂ g = 5-3 = 2, G = ₃ 7-5 = 2, ₄ g = 11-7 = 4, e assim por diante. A sequência _(n g) de diferenças principais tem sido extensivamente estudada.

Para qualquer número natural n maior do que 1, a sequência (para a notação N! Ler fatorial )

N! 2 +, N! + 3, ..., N! + N

é uma sequência de N - 1 inteiros compostos consecutivos. Portanto, não existem folgas entre primos que são arbitrariamente grande, isto é, para qualquer número natural n, se n é um número inteiro com g _n> N. (Escolha n de modo que p _n é o maior número primo menos de N! + 2.)

Por outro lado, as lacunas obter arbitrariamente pequena em relação aos números primos: o quociente de g _n / p _n se aproxima de zero como N se aproxima do infinito. Note também que a conjectura dos primos gêmeos afirma que g _n = 2 para infinitamente muitos inteiros n.

Localização do maior primo conhecido

Wikinews tem notícias relacionadas: CMSU equipe de computação descobre outro tamanho de registro principal

Wikinews tem notícias relacionadas: A computação distribuída descobre maior primo conhecido

O maior primo conhecido, a partir de agosto de 2007, é de 2 ^32.582.657 - 1 (este número é 9.808.358 dígitos); é o 44º conhecido Primo de Mersenne. M _32582657 foi encontrado 4 de setembro de 2006 por Curtis Cooper e Steven Boone, professores da Universidade do Missouri Central (anteriormente Central Missouri State University) e membros de um esforço de colaboração conhecido como GIMPS. Antes de encontrar a prima, Cooper Boone e executou o software GIMPS em um pico de 700 computadores da universidade para 9 anos.

Os próximos dois maiores números primos conhecidos são também Mersenne Primes: M = _30.402.457 ^30.402.457 2 - 1 (43 conhecido Primo de Mersenne, 9.152.052 dígitos) e M = _25.964.951 ^25.964.951 2 - 1 (42 conhecido Primo de Mersenne, 7.816.230 dígitos). Historicamente, o primeiro maior conhecido tem sido quase sempre um primo Mersenne desde o início dos computadores eletrônicos, porque não existe um teste de primalidade particularmente rápido para os números desta forma, o Teste de Lucas-Lehmer para números de Mersenne.

O maior primo conhecido que não é um número primo Mersenne é 19249 × 2 + 1 ^13.018.586 (3.918.990 dígitos), um Número PROTH. Esta é também a sétima maior primo conhecido de qualquer forma. Foi encontrado no 26 de Março de 2007 pela Dezessete ou projeto Bust e lhes traz um passo mais perto de resolver o Sierpinski problema.

Alguns dos maiores números primos conhecidos não ter qualquer forma particular (isto é, nenhuma fórmula simples, tais como a de números primos Mersenne) ter sido encontrado tomando um pedaço de dados binários semi-aleatórios, convertendo-a em um número n, multiplicando-o pela 256 ^K por algum número inteiro positivo k, e procurando possíveis primos dentro do intervalo [256 ^k n + 1, 256 ^K (n + 1) - 1].

Prêmios para encontrar números primos

O Electronic Frontier Foundation (EFF) ofereceu um prêmio de US $ 100.000 para os primeiros descobridores de um primo com pelo menos 10 milhões de dígitos. Eles também oferecem 150 mil dólares para 100 milhões de dígitos, e US $ 250.000 para 1 bilhão de dígitos. Em 2000, pagou US $ 50.000 para 1.000.000 dígitos.

O RSA Factoring Desafio ofereceu prêmios de até US $ 200.000 para encontrar os fatores primos de certa semiprimes de até 2048 bits. No entanto, o desafio foi fechada em 2007, após prêmios muito menores para semiprimes menores tinha sido pago.

Generalizações do conceito nobre

O conceito de número primo é tão importante que tem sido generalizada de formas diferentes nos vários ramos da matemática.

Elementos principais em anéis

Pode-se definir elementos de primeira linha e elementos irredutíveis em qualquer domínio integral. Para qualquer domínio fatoração única, como o Z anel dos inteiros, o conjunto de elementos principais é igual ao conjunto de elementos irredutíveis, que para Z é {..., -11, -7, -5, -3, -2, 2, 3, 5, 7, 11, ...}.

Como um exemplo, considera-se o Inteiros de Gauss Z [i], isto é, números complexos da forma a + bi com a e b em Z. Este é um domínio integral, e os seus elementos principais são o Primes de Gauss. Note-se que 2 não é um número primo Gaussiana, porque os factores para o produto de dois números primos os Gaussianas (1 + i) e (1 - i). O elemento 3, no entanto, continua a ser privilegiada nas inteiros de Gauss. Em geral, os primos racionais (ou seja, elementos principais no Z anel de inteiros) do formulário de 4 k + 3 são primos gaussianos, enquanto primos racionais da forma 4 k + 1 não são.

Ideais primos

Em teoria dos anéis, um geralmente substitui a noção de número com o de ideal. Ideais primos são uma importante ferramenta e objeto de estudo em álgebra comutativa, teoria dos números algébricos e geometria algébrica. Os ideais primos do anel de números inteiros são as ideais (0), (2), (3), (5), (7), (11), ...

Um problema central na teoria dos números algébricos é como um fatores ideais privilegiada quando é levantada para um campo de extensão. Por exemplo, no exemplo acima inteiro Gaussian, (2) se ramifica em uma potência prime (1 + i e 1 - i geram o mesmo ideal prime), ideais primos da forma (4 k + 3) são inertes (permanecer prime) e ideais primos da forma (4 k + 1) split (são o produto de dois ideais primos distintos).

Primes na teoria de avaliação

Em teoria do campo de classe ainda outra generalização é usada. Dada uma arbitrária campo K, considera- valorações sobre K, certas funções de K aos números reais R. Toda essa avaliação produz uma topologia em K, e duas avaliações são chamados equivalentes se deu a mesma topologia. Um primo de K (às vezes chamado de um lugar de K) é uma classe de equivalência de avaliações. Com esta definição, os primos do campo Q de números racionais são representados pela norma valor absoluto da função (conhecida como o "prime infinita"), bem como pela p valorizações -adic sobre Q, para cada número primo p.

Nós Prime

Em teoria do nó , um nó principal é um nó que é, em certo sentido, indecomponível. Especificamente, é um que não pode ser escrita como o soma nó de dois nós não triviais.

Perguntas abertas

Há muitas questões em aberto sobre números primos. Um aspecto muito importante é a Hipótese de Riemann, que basicamente diz que os números primos são tão regularmente distribuídos possível. De um ponto de vista físico, aproximadamente afirma que a irregularidade na distribuição de números primos só vem de ruído aleatório. Do ponto de vista matemático, ele afirma que cerca a distribuição assintótica dos números primos (cerca de 1 / x log de números menores que x são primos, os teorema de número primo) também é válida para intervalos mais curtos de comprimento sobre a raiz quadrada de x (para intervalos próximos x). Esta hipótese é geralmente consideradas correctas, em particular, a hipótese mais simples é que primos não deve ter irregularidades significativas sem uma boa razão.

Muitas conjecturas famosas parecem ter uma muito alta probabilidade de ser verdadeira (em um sentido formal, muitos deles decorrem argumentos probabilísticos heurísticos simples):

• Primordial Números de Euclides: não se sabe se há ou não um número infinito de números primos Euclides.

• Forte conjectura de Goldbach : Todo mesmo número inteiro maior que 2 pode ser escrito como uma soma de dois primos.

• Fraco conjectura de Goldbach: Cada número inteiro ímpar maior do que 5 pode ser escrito como uma soma de três primos.

• Conjectura dos primos gêmeos: Há infinitamente muitos gêmeo primos, pares de números primos com diferença 2.

• A conjectura de Polignac: Para cada inteiro positivo n, existem infinitos pares de números primos consecutivos que diferem por 2 n. Quando n = 1 esta é a conjectura dos primos gêmeos.

• A forma mais fraca da conjectura de Polignac: Every mesmo número é a diferença de dois números primos.

• Acredita-se amplamente existem infinitos Primos de Mersenne, mas não Fermat primos.

• Conjectura-se há infinitos números primos da forma ² n + 1.

• Muitas conjecturas conhecidos são casos especiais da ampla De Schinzel hipótese H.

• Conjectura-se que existem infinitos Fibonacci primos.

• A conjectura de Legendre: Há um número primo entre ² e n (n + 1) ² para cada inteiro positivo n.

• A conjectura de Cramér: . Esta conjectura implica Legendre de, mas o seu estatuto é mais incerto.

• A conjectura de Brocard: Há sempre pelo menos quatro primos entre as praças de números primos consecutivos superiores a 2.

Todos os quatro Problemas de Landau de 1912 estão listados acima e ainda sem solução: Goldbach, primos gémeos, Legendre, n ² 1 primos.

Aplicações

Por um longo tempo, teoria dos números, em geral, bem como o estudo de números primos em particular, foi visto como o exemplo canônico da matemática pura, sem aplicações fora do auto-interesse de estudar o tema. Em particular, os teóricos dos números, tais como britânico matemático GH Hardy orgulhavam-se de fazer um trabalho que não tinha absolutamente nenhum significado militar. No entanto, esta visão foi quebrada na década de 1970, quando foi anunciado publicamente que os números primos poderiam ser usados como base para a criação de algoritmos de criptografia de chave pública. Os números primos são também utilizados para tabelas de hash e geradores de números pseudo-aleatórios.

Alguns máquinas de rotor foram concebidos com um número diferente de pinos de cada rotor, com o número de pinos de rotor de qualquer uma ou prima, ou coprime ao número de pinos em qualquer outro rotor. Isto ajudou a gerar ciclo completo de posições possíveis do rotor antes de repetir qualquer posição.

Criptografia de chave pública

Vários algoritmos de criptografia de chaves públicas, tais como RSA, são baseados em números primos grandes (por exemplo, com 512 bits).

Os números primos na natureza

Muitos números ocorrem na natureza, e, inevitavelmente, alguns deles são primos. Existem, no entanto, relativamente poucos exemplos de números que aparecem na natureza, porque eles são primos. Por exemplo, a maioria estrela do mar tem cinco braços, e 5 é um número primo. Entretanto, não há evidências que sugerem que estrelas do mar tem cinco braços porque 5 é um número primo. De fato, algumas estrelas do mar têm números diferentes de armas. Echinaster luzonicus normalmente tem seis braços, Luidia senegalensis tem nove braços, e Solaster Endeca pode ter até vinte braços. Por que a maioria das estrelas do mar (ea maioria dos outros equinodermos) têm simetria cinco vezes permanece um mistério.

Um exemplo do uso de números primos na natureza é como uma estratégia evolutiva usado por cigarras do género Magicicada. Esses insetos passam a maior parte de suas vidas como subterrâneo larvas. Eles só pupa e depois saem de suas tocas, após 13 ou 17 anos, altura em que eles voam sobre, raça, e depois morrer depois de algumas semanas, no máximo. A lógica para o que se acredita ser a de que os intervalos de números primos entre emergências torna muito difícil para os predadores para evoluir que pode especializar-se como predadores em Magicicadas . Se Magicicadas apareceu em um intervalos de números não primos, dizer a cada 12 anos, em seguida, predadores aparecendo a cada 2, 3, 4, 6, ou 12 anos seria certo para encontrá-los. Durante um período de 200 anos, as populações de predadores médios durante surtos hipotéticos de 14 e 15 anos cigarras seria até 2% maior do que durante os surtos de cigarras 13 e 17 anos. Embora pequena, esta vantagem parece ter sido suficiente para conduzir a seleção natural em favor de um ciclo de vida prime-contada, por esses insetos.

Especula-se que os zeros da função zeta estão ligados aos níveis de energia de sistemas complexos de quantum.

Os números primos nas artes e literatura

Os números primos têm influenciado muitos artistas e escritores. O Francês compositor Olivier Messiaen usadas números primos para criar música ametrical através de "fenômenos naturais". Em obras como La du Seigneur Nativité (1935) e Quatre études de rythme (1949-1950), ele emprega simultaneamente motivos com comprimentos dadas por diferentes números primos para criar ritmos imprevisíveis: os primos 41, 43, 47 e 53 aparecem em um dos Études. De acordo com Messiaen esta forma de composição foi "inspirada nos movimentos da natureza, movimentos de durações gratuitos e desiguais".

Em seu romance de ficção científica de contato, mais tarde transformado em umfilme de mesmo nome, aNASAcientistaCarl Sagansugeriu que os números primos poderia ser usado como um meio de comunicação com os estrangeiros, uma idéia que ele tinha desenvolvido primeiro informalmente com astrônomo americanoFrank Drake em 1975.

De Tom Stoppard premiado jogo 1993 Arcadia era uma tentativa consciente para discutir idéias matemáticas no palco. Na cena de abertura, os 13 anos de idade quebra-cabeças mais heroína último teorema de Fermat , um teorema que envolve números primos.

Muitos filmes refletem um fascínio popular com os mistérios dos números primos e criptografia: filmes como The Cube, Sneakers, O Espelho Tem Duas Facese Uma Mente Brilhante, baseado na biografia do matemático e prêmio NobelJohn Nash Forbes porSylvia Nasar.