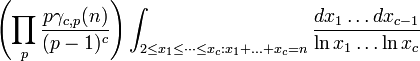A conjectura de Goldbach

Assuntos Relacionados: Matemática

Sobre este escolas selecção Wikipedia

Esta seleção é feita para as escolas de caridade infantil leia mais . Você quer saber sobre o patrocínio? Veja www.sponsorachild.org.uk

A conjectura de Goldbach é uma das mais antigas problemas não resolvidos em teoria dos números e em toda a matemática . Ele afirma:

Cada mesmo número inteiro maior do que 2 pode ser escrita como a soma de dois números primos .

Expressando um dado mesmo número como uma soma de dois primos é chamado de Goldbach partição do número. Por exemplo,

4 = 2 + 2

6 = 3 + 3

8 = 3 + 5

10 = 3 + 7 + = 5 5

12 = 5 + 7

14 = 11 = 3 + 7 + 7

...

Em outras palavras, a conjectura de Goldbach afirma que cada número par maior do que ou igual a quatro é um número de Goldbach, um número que pode ser expresso como a soma de dois números primos. Veja também A conjectura de Levy.

Uma ilustração da conjectura de Goldbach.

Origins

Em 7 de junho de 1742, o Prussiano matemático Christian Goldbach escreveu uma carta a Leonhard Euler (carta XLIII) no qual ele propôs a seguinte conjectura:

Cada número inteiro maior do que 2 pode ser escrita como a soma de três números primos.

Ele considerou um a ser um número primo , uma convenção posteriormente abandonado. Uma versão moderna da conjectura original de Goldbach é:

Cada número inteiro maior do que 5 pode ser escrito como a soma de três números primos.

Euler, tornando-se interessado no problema, respondeu, observando que esta conjectura é equivalente com outra versão:

Cada mesmo número inteiro maior do que 2 pode ser escrita como a soma de dois números primos,

acrescentando que ele considerava esta uma inteiramente certo teorema ("ein ganz gewisses Theorema"), apesar de ele ser incapaz de provar isso.

Versão de Euler é a forma em que a conjectura é normalmente expressa hoje. É também conhecido como o " forte "," até mesmo ", ou" binário "Goldbach conjectura, para distingui-lo de um corolário mais fraca. A forte conjectura de Goldbach implica a conjectura de que todos os números ímpares superiores a 7 são a soma de três primos ímpares, que é conhecido hoje como variadamente o "Fraco" conjectura de Goldbach, o "estranho" Goldbach conjectura, ou o "ternário" Goldbach conjectura. Ambas as questões têm permanecido sem solução desde então, embora a forma fraca da conjectura parece ser muito mais perto do que a resolução forte. Se o forte conjectura de Goldbach é verdadeira, a fraca conjectura de Goldbach será verdade por implicação.

Resultados verificados

Para pequenos valores de n, a conjectura de Goldbach forte (e, consequentemente, a fraca conjectura de Goldbach) pode ser verificada directamente. Por exemplo, N. Pipping em 1938 laboriosamente verificada a conjectura até $n \ leq 10 ^ 5$ . Com o advento dos computadores, muitos mais pequenos valores de n foram verificados; T. Oliveira e Silva está executando uma busca no computador distribuído, que verificou a conjectura para $n \ leq 10 ^ {18}$ .

A conjectura de Goldbach não diz que um número deve ser a soma de um único par de números primos. Os exemplos deste artigo mostram que mais do que um par de números primos podem somar o mesmo número.

Justificativa heurística

Considerações estatísticas que incidem sobre o distribuição probabilística dos números primos presente evidência informal em favor da conjectura (em ambas as formas fracas e fortes) para suficientemente grandes números inteiros: quanto maior for o número inteiro, os mais formas não estão disponíveis para esse número a ser representado como a soma de dois ou três outros números, e o mais "provável" torna-se que pelo menos uma destas representações consiste inteiramente de primos .

Número de maneiras de escrever um número par n como a soma de dois números primos (4 ≤ n ≤ 1,000)

Número de maneiras de escrever um número par n como a soma de dois números primos (4 ≤ n ≤ 1.000.000)

Uma versão muito grosseira do argumento probabilístico heurística (para a forma forte da conjectura de Goldbach) é a seguinte. O teorema de número primo afirma que um inteiro m selecionados aleatoriamente tem cerca de um $1 / \ ln m \, \!$ chance de ser privilegiada. Assim, se o símbolo n representa um número inteiro par grande e m é um número entre 3 e n / 2, em seguida, pode-se esperar que a probabilidade de m e nm sendo simultaneamente nobre ser $1 \ grande / \ grande [\ ln m \, \ ln (n-m) \ grande]$ . Esta heurística é não rigorosa de um número de razões; por exemplo, ele assume que os eventos que M e 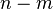$n-m$ são primos são estatisticamente independentes umas das outras. No entanto, se alguém persegue essa heurística, pode-se esperar que o número total de maneiras de escrever um grande n inteiro par como a soma de dois números primos ímpares para ser mais ou menos

$\ Sum_ {3} = m ^ {n / 2} \ frac {1} {\ ln m} {1 \ over \ ln (nm)} \ approx \ frac {n} {2 \ ln ^ 2 n}.$

Uma vez que esta quantidade vai para o infinito quando n aumenta, esperamos que todos os grandes inteiro par tem não apenas uma representação como a soma de dois números primos, mas na verdade tem muito muitas dessas representações.

O argumento heurística acima é, na verdade, um pouco imprecisos, porque ignora alguma dependência entre os eventos de m e 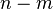$n-m$ ser primo. Por exemplo, se m for ímpar, então 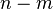$n-m$ também é ímpar, e, se m é par, então 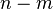$n-m$ é ainda, uma relação não-trivial porque (além de 2) apenas números ímpares podem ser privilegiada. Do mesmo modo, se n é divisível por três, e m um número primo já foi distinta da 3, então 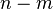$n-m$ também seria coprime a 3 e, assim, ser ligeiramente mais susceptíveis de ser primo do que um número geral. Prosseguindo este tipo de análise com mais cuidado, Hardy e Littlewood em 1923 conjecturou (como parte de seu famoso Hardy-Littlewood tupla principal conjectura) que, para qualquer fixo c ≥ 2, o número de representações de um grande número inteiro n como a soma dos números primos c 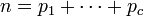$n = p_1 + \ dotsb + p_c$ com $p_1 \ leq \ dotsb \ leq p_c$ Deve ser assintoticamente igual

$\ Left (\ prod_p \ frac {p \ gamma_ {c, p} (n)} {(p-1) ^ c} \ right) \ int_ {2 \ Leq x_1 \ Leq \ dotsb \ leq x_c: x_1 + \ ldots + x_c = n} \ frac {dx_1 \ ldots dx_ {c-1}} {\ ln x_1 \ ldots \ ln x_c}$

onde o produto é sobre todos primos p, e $\ Gamma_ {c, p} (n)$ é o número de soluções para a equação $n = q_1 + \ ldots + q_c \ mod p$ na aritmética modular , sujeito à restrições $q_1, \ ldots, q_c \ neq 0 \ mod p$ . Esta fórmula foi rigorosamente provado ser assintoticamente válida para c ≥ 3 do trabalho de Vinogradov, mas ainda é apenas uma conjectura quando $c = 2$ . Neste último caso, a fórmula anterior simplifica a 0 quando n é ímpar, e

$2 \ Pi_2 \ left (\ Prod_ {p | n; p \ geq 3} \ frac {p-1} {p-2} \ right) \ int_2 ^ n \ frac {dx} {\ ln ^ 2 x} \ cerca de 2 \ Pi_2 \ left (\ Prod_ {p | n; p \ geq 3} \ frac {p-1} {p-2} \ right) \ frac {n} {\ ln ^ 2 n}$

quando n é par, onde $\ Pi_2$ é o constante dos primos gêmeos

$\ Pi_2: = \ Prod_ {p \ geq 3} \ left (1 - \ frac {1} {(p-1) ^ 2} \ right) = 0,6601618158 \ ldots.$

Este assintótica é conhecida como a conjectura de Goldbach prorrogado. A forte conjectura de Goldbach é, de facto, muito semelhante à conjectura dos primos gêmeos, e as duas conjecturas se acredita serem de dificuldade aproximadamente comparável.

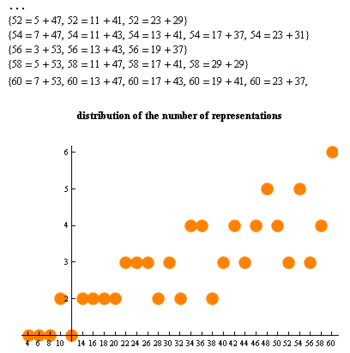
As funções de partição mostrados aqui podem ser apresentadas como histogramas que ilustram informatively as equações acima. Ver Cometa de Goldbach.

Resultados rigorosos

O fraca conjectura de Goldbach é bastante perto de resolução.

A forte conjectura de Goldbach é muito mais difícil. O trabalho de Vinogradov em 1937 e Theodor Estermann (1902-1991) em 1938 mostraram que quase todos os números pares pode ser escrito como a soma de dois números primos (no sentido em que a fracção de números pares, que podem ser escritas de modo tende para 1). Em 1930, Lev Schnirelmann provado que cada número par n ≥ 4 pode ser escrito como a soma de, no máximo, 300.000 primos. Este resultado foi posteriormente melhorado por muitos autores; Atualmente, o resultado mais conhecido é devido a Olivier Ramare, que em 1995 mostrou que cada número par n ≥ 4 é, de facto, a soma de no máximo seis primos. De facto, a resolução de fraca conjectura de Goldbach também implica directamente que cada número par n ≥ 4 é a soma de, no máximo, quatro primos.

Chen Jingrun mostraram em 1973, utilizando os métodos de teoria que cada peneira suficientemente grande mesmo número pode ser escrito como a soma de dois números primos tanto, ou um primo e um semiprimo (o produto de dois números primos) -por exemplo, de 100 = 23 + 7 · 11.

Em 1975, Hugh Montgomery e Robert Charles Vaughan mostrou que "a maioria dos" números pares eram expresso como a soma de dois números primos. Mais precisamente, eles mostraram que não existiam constantes positivas 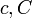$C, C$ de tal modo que para todos os números suficientemente grandes de N, cada mesmo número menor do que N é a soma de dois números primos, com no máximo 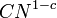$C N ^ {1-c}$ exceções. Em particular, o conjunto de inteiros pares que não são a soma de dois números primos tem densidade zero.

Roger Heath-Brown e Jan-Christoph Schlage-Puchta mostrou em 2002 que cada suficientemente grande mesmo número inteiro é uma soma de dois primos e exatamente 13 potências de 2.

Pode-se fazer perguntas semelhantes quando primes são substituídos por outros conjuntos especiais de números, como as praças. Por exemplo, foi comprovada por Lagrange que cada número inteiro positivo é a soma de quatro quadrados. Ver O problema de Waring.

Provas tentados

Tal como acontece com muitas conjecturas famosos em matemática, há uma série de supostas provas da conjectura de Goldbach, nenhum dos quais estão atualmente aceita pela comunidade matemática.

Porque ele é facilmente entendido por leigos, a conjectura de Goldbach é um alvo popular para os matemáticos amadores, que muitas vezes tentam provar ou refutar-lo usando apenas a matemática de alto nível-escola. Ele compartilha esse destino com o teorema de quatro cores e último teorema de Fermat , os quais também têm um problema facilmente afirmado, mas, no entanto, parecem ser resolvidas somente através de métodos extremamente elaborados.

Na cultura popular

Para gerar publicidade para o livro O tio Petros e Conjectura de Goldbach por Apostolos Doxiadis, editora britânica Tony Faber ofereceu um prêmio de US $ 1.000.000 para uma prova da conjectura em 2000, se a prova foi apresentado antes de Abril de 2002. O prêmio nunca foi reclamado.
O drama de televisão Lewis contou com um professor de matemática na Universidade de Oxford , que havia vencido a Campos medalha por seu trabalho sobre a conjectura de Goldbach, que era uma característica trama principal.
Conto de Isaac Asimov "Sessenta milhões de Trillion Combinações" apresentou um matemático que suspeitava que seu trabalho sobre a conjectura de Goldbach tinha sido roubado.
No Filme espanhol "La habitación de Fermat" (2007), dirigido por Luis Piedrahita e Rodrigo Sopeña, um jovem matemático afirma ter solucionado a conjectura.

Retirado de " http://en.wikipedia.org/w/index.php?title=Goldbach%27s_conjecture&oldid=208155239 "

Home Page - YouTube Channel