
Quatro cor teorema
Você sabia ...
Crianças SOS feita esta seleção Wikipedia ao lado de outros recursos escolas . patrocínio SOS Criança é legal!

O teorema de quatro cores (também conhecido como o teorema de quatro cores mapa) afirma que, dada qualquer plano separado em regiões, como um mapa político dos estados de um país, as regiões podem ser coloridos usando há mais de quatro cores de tal forma que não há duas regiões adjacentes receber a mesma cor. Duas regiões são chamados adjacentes somente se eles compartilham um segmento de fronteira, não apenas um ponto. Cada região deve ser contíguas, isto é, que não podem ter exclaves como alguns países reais, tais como Angola , Azerbaijão , o Estados Unidos ou Rússia .
É frequentemente o caso que o uso de apenas três cores é inadequada. Isto já se aplica ao mapa com uma região cercada por três outras regiões (embora com um número par de países vizinhos três cores são o suficiente) e não é de todo difícil de provar que cinco cores são suficientes para colorir um mapa.
A cor quatro teorema foi a primeira grande teorema de ser provado usando um computador, bem como a prova não é aceita por todos os matemáticos, porque seria inviável para um ser humano para verificar a mão (ver prova assistida por computador). Em última análise, a fim de acreditar na prova, um tem que ter fé na correcção do e compilador hardware executar o programa utilizado para a prova.
A percepção de falta de elegância matemática pela comunidade matemática geral foi outro fator, e parafraseando comentários do tempo, "uma boa prova matemática é como um poema-este é um lista telefônica! "
História
O conjectura foi proposta pela primeira vez em 1852, quando Francis Guthrie, ao tentar colorir o mapa de condados de Inglaterra , percebeu que eram necessários apenas quatro cores diferentes. Na época, o irmão de Guthrie, Fredrick, era um estudante de Augustus De Morgan em College University. Francis perguntou com Fredrick sobre ele, que, em seguida, levou-a para DeMorgan. (Fredrick Guthrie formou mais tarde, em 1852, e mais tarde tornou-se professor de matemática na África do Sul ). De acordo com De Morgan:
Um aluno meu [Guthrie] me pediu hoje para dar-lhe uma razão para um fato que eu não sabia que era um fato - e não fazer ainda. Ele diz que se uma figura de qualquer maneira ser dividida e os compartimentos de cor diferente para que figuras com qualquer parte da linha de fronteira comum são de cor diferente - quatro cores podem ser querido, mas não mais-o seguinte é o caso em que quatro cores estão queria. Consulta pode não uma necessidade para cinco ou mais ser inventado ...
A primeira referência publicada é de Arthur Cayley, que por sua vez credita a conjectura de De Morgan.
Houve várias tentativas falhadas de início de provar o teorema . Uma prova do teorema foi dada pelo Alfred Kempe em 1879, que foi amplamente aclamado; outra prova foi dada por Peter Guthrie Tait em 1880. Não foi até 1890 que a prova de Kempe foi mostrado incorreta por Percy Heawood, e 1891 que a prova de Tait foi mostrado incorreta por Julius Petersen-cada prova falsa ficou incontestado por 11 anos.
Em 1890, além de expor a falha na prova de Kempe, Heawood provou que tudo grafos planares são cinco ilusório; ver cinco teorema cor.
Resultados significativos foram produzidos pelo croata matemático Danilo Blanuša na década de 1940, encontrando um original snark.
Durante a década de 1960 e 1970 alemão matemático Heinrich Heesch desenvolveram métodos de aplicação do computador em busca de uma prova.
Não foi até 1976 que a conjectura das quatro cores foi finalmente comprovada por Kenneth Appel e Wolfgang Haken no Universidade de Illinois. Eles foram atendidos em algum trabalho algorítmico por John Koch.
Se a conjectura das quatro cores eram falsas, haveria pelo menos um mapa com o menor número possível de regiões que requer cinco cores. A prova mostrou que um contra tais mínima não pode existir através do uso de dois conceitos técnicos:
- Um conjunto inevitável contém regiões de tal forma que cada mapa tem de ter pelo menos uma região a partir desta coleção.
- Uma configuração redutível é um arranjo de países que não podem ocorrer em um contra-exemplo minimal. Se um mapa contém uma configuração redutível, e o resto do mapa pode ser colorido com quatro cores, em seguida, todo o mapa pode ser colorido com quatro cores e de modo que este mapa não é mínima.
Utilizando as regras e procedimentos matemáticos com base nas propriedades de configurações redutíveis (por exemplo, a método de descarga, anéis, correntes Kempe, etc.), Appel e Haken encontrado um conjunto de configurações redutíveis inevitável, provando assim que um contra-mínimo para a conjectura de quatro cores não poderia existir. Sua prova reduziu a infinitude de possíveis mapas para 1936 configurações redutíveis (posteriormente reduzida para 1476), que tiveram de ser verificadas uma a uma por computador. Esta parte redutibilidade do trabalho foi o dobro verificado de forma independente com diferentes programas e computadores. No entanto, a parte inevitabilidade da prova foi mais de 500 páginas de escritos a mão contra-contra-exemplos, muito do que foi o filho adolescente de Haken Lippold verificação corantes gráfico. O programa de computador correu por centenas de horas.
Desde a prova do teorema, algoritmos eficientes foram encontrados para mapas de 4 colorir necessitando apenas O (n 2), onde n é o número de vértices. Em 1996 , Neil Robertson, Daniel P. Sanders, Paul Seymour, e Robin Thomas criado um algoritmo de tempo quadrática, utilizando O trabalho de Edward Belaga para melhorar um algoritmo quartic com base em prova de Appel e Haken. Esta nova prova é semelhante a Appel e Haken de mas mais eficiente porque a reduzida complexidade do problema e necessário verificar apenas 633 configurações redutíveis. Ambas as partes inevitabilidade e redutibilidade desta nova prova deve ser executado por computador e são impraticáveis para verificar a mão.
Em 1980, George Spencer-Brown depositou sua suposta prova do teorema de quatro cores no mapa Royal Society. A validade dessa prova, o que torna-se Anexo 5 da tradução alemã de seu livro " Leis da Forma "(Lübeck 1997), é geralmente posta em dúvida.
Em 2004 Benjamin e Werner Georges Gonthier formalizou uma prova do teorema dentro do Coq assistente de prova (Gonthier, sd). Isso elimina a necessidade de confiar os vários programas de computador utilizados para verificar a casos particulares; só é necessário confiar o kernel Coq.
Também há algoritmos eficientes para determinar se uma ou duas cores suficientes para colorir um mapa. Determinar se três cores são suficientes é, no entanto, NP-completo, e por isso um algoritmo rápido é improvável. Determinar se um general (possivelmente não-planar) gráfico pode ser 4-colorido é de igual modo NP-completo.
Não é para cartógrafos
Embora o teorema de quatro cores foi descoberto no processo de coloração de um verdadeiro mapa, é raramente utilizado na prática cartografia. De acordo com Kenneth maio, um historiador matemático que estudou uma amostra de atlas na Biblioteca do Congresso, não há uma tendência para minimizar o número de cores utilizadas. Muitos mapas usar a cor para outras regiões políticas do que as coisas. A maioria dos mapas utilizar mais do que quatro cores, e quando apenas quatro cores são utilizadas, geralmente, o número mínimo de cores é realmente necessários menos de quatro.
Na maioria dos mapas reais existem lagos, que devem ser todos da mesma cor. Este é, então, adicional ao que quer que as cores são necessárias para regiões políticas. Se os lagos são contadas como uma única região, o teorema não se aplica. Ele pode ser aplicado a áreas de terra do mapa sozinho, considerando os lagos como não pertencentes ao mapa das regiões, mas em vários mapas reais não- regiões contíguas mapa pode, além disso pertencem a um único não- conectado região política e exigem a mesma cor (veja abaixo ), por isso, então outra vez o teorema não se aplica.
Livros sobre cartografia ea história da cartografia não menciona o teorema de quatro cores, embora mapa coloração é um tema de discussão. Geralmente, os cartógrafos dizem que estão mais preocupados com coloração mapas políticos, de forma equilibrada, de modo que nenhuma única cor domina. Se eles usam quatro, cinco, ou mais cores não é uma preocupação primordial.
Declaração formal em teoria dos grafos
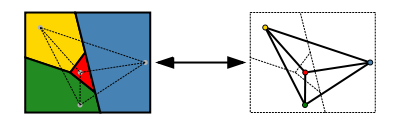
Para indicar formalmente o teorema, é mais fácil de reformulá-la em teoria dos grafos. Em seguida, ele afirma que o vértices de cada grafo planar pode ser colorida com, no máximo, quatro cores de modo que não há dois vértices adjacentes receber a mesma cor. Ou "cada gráfico planar é de quatro ilusório" para breve. Aqui, todas as regiões do mapa é substituído por um vértice do gráfico, e dois vértices estão ligados por uma borda se e somente se as duas regiões compartilham um segmento de fronteira (e não apenas um canto).
Refutações falsos
Como muitos famosos problemas em aberto da matemática, o teorema de quatro cores tem atraído um grande número de falsos provas e refutações na sua longa história. Alguns, como Kempe de Tait e do mencionado acima, ficou sob escrutínio público por mais de uma década antes que eles foram expostos. Mas muitos mais, de autoria de amadores, nunca foram publicados.
 |  |
| Este mapa foi colorido com cinco cores ... | ... Mas é necessário para mudar, pelo menos, quatro dos dez regiões para obter uma coloração com apenas quatro cores. |
Geralmente, o mais simples "contra-exemplos" tentativa de criar uma região que toca todas as outras regiões. Isso força as restantes regiões para ser colorido com apenas três cores. Porque o teorema das quatro cores é verdade, este é sempre possível; no entanto, porque a pessoa que desenha o mapa está focada em um grande região, eles não conseguem perceber que as regiões restantes podem de fato ser colorido com três cores.
Este truque pode ser generalizada: há muitos mapas onde se as cores de algumas regiões são selecionados de antemão, torna-se impossível para colorir as restantes regiões sem exceder quatro cores. Um verificador casual do contra-exemplo não pode pensar para alterar as cores dessas regiões, para que o contra-exemplo vai aparecer como se ele é válido.
Talvez um efeito subjacente a este equívoco comum é o facto de a cor não é restrição transitivo: a região só tem que ser uma cor diferente dos regiões que toca diretamente, e não regiões tocando regiões que ele toca. Se este fosse o de restrição, gráficos planares exigiria arbitrariamente grande número de cores.
Outros falsos refutações violar os pressupostos do teorema de maneiras inesperadas, tais como a utilização de uma região que consiste em várias partes desconexas, ou não permitindo regiões da mesma cor de tocar em um ponto.
Generalizações


Pode-se também considerar o problema de coloração em outras superfícies do que o avião . O problema na esfera ou cilindro é equivalente ao que no avião. Para fechada (orientável ou não orientável) superfícies com positiva género, o número máximo de cores p necessários depende da superfície da característica de Euler χ de acordo com a fórmula
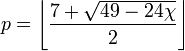 ,
,
em que os suportes mais exteriores denotar o função chão. A única exceção a fórmula é a garrafa de Klein , que tem característica Euler 0 e requer 6 cores. Esta foi inicialmente conhecido como o Conjectura Heawood e provou como O Mapa Cor Teorema por Gerhard Ringel e JTW Youngs em 1968.
Alternativamente, para uma superfície orientável a fórmula pode ser determinado em termos da género de uma superfície, g:
Por exemplo, o toro tem característica de Euler χ = 0 (género e g = 1) e, portanto, p = 7, de modo que não há mais do que sete cores são obrigados a colorir qualquer mapa num toro.
A Fita de Möbius também requer seis cores.
Não há nenhuma extensão útil do problema de coloração para regiões sólidas tridimensionais. É trivial para a construção de um conjunto de n hastes flexíveis, por exemplo, de tal modo que cada haste toca cada outra haste. O conjunto exigira, então, n cores, ou n + 1 se você considerar o espaço vazio que também toca em cada haste. n pode ser feita para ser qualquer número inteiro, tão grande quanto desejado.
Regiões não contíguas

No mundo real, nem todos os países são contíguos (por exemplo, Alaska como parte do Estados Unidos , Nakhchivan como parte do Azerbaijão , e Kaliningrad como parte da Rússia ). Se o esquema de cores escolhido requer que o território de um país em particular deve ser da mesma cor, quatro cores podem não ser suficientes. Por exemplo, considere um mapa simplificado:
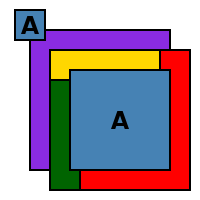
Neste mapa, as duas regiões marcados A pertencem ao mesmo país, e deve ser da mesma cor. O mapa então requer cinco cores, uma vez que as duas regiões em conjunto são contíguos com outros quatro regiões, cada uma das quais é contígua com todos os outros. Se A consistia em três regiões, seis ou mais cores pode ser necessária; pode-se construir mapas que necessitam de um número arbitrariamente alta de cores.

