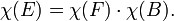Euler característica

Em matemática , e mais especificamente na topologia algébrica e combinatória poliédrica, a característica de Euler (ou característica de Euler-Poincaré) é uma invariante topológico, um número que descreve um forma ou estrutura do espaço topológico, independentemente da forma como ele é dobrado. É comumente designado por ( letra grega chi).

A característica de Euler foi originalmente definido para poliedros e usado para provar vários teoremas sobre eles, incluindo a classificação dos sólidos platônicos . Leonhard Euler , para quem o conceito é chamado, foi responsável por grande parte deste trabalho precoce. Em matemática moderna, a característica Euler surge de homologia e conecta-se a muitos outros invariantes.

Poliedros

A característica de Euler foi classicamente definido para as superfícies de poliedros, de acordo com a fórmula

em que V, E, e F são, respectivamente, os números de vértices (cantos), e bordas enfrenta no poliedro dado. Qualquer superfície de poliedros convexos tem característica Euler

Este resultado é conhecida como fórmula de Euler. Isto corresponde à característica de Euler da esfera (que é 2), e aplica-se de forma idêntica às poliedros esférica. Uma ilustração da fórmula em alguns poliedros é dada abaixo.

Nome	Imagem	Vértices V	Edges E	Faces F	Euler característica: V - E + F
Tetraedro		4	6	4	2
Hexahedron ou cubo		8	12	6	2
Octaedro		6	12	8	2
Dodecaedro		20	30	12	2
Icosahedron		12	30	20	2

As superfícies dos poliedros não-convexa pode ter várias características Euler;

Nome	Imagem	Vértices V	Edges E	Faces F	Euler característica: V - E + F
Tetrahemihexahedron		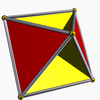6	12	7	1
Octahemioctahedron		12	24	12	0
Cubohemioctahedron		12	24	10	-2
Grande icosaedro		12	30	20	2

Uma forma modificada de fórmula de Euler, usando poliédrica densidade (D) e densidade do polígono figuras de vértice ( ) E rostos ( ) Foi dada por Arthur Cayley, e mantém, tanto para poliedros convexa (em que os factores de correcção são todos 1), e o não-regular convexo Poliedros Kepler-Poinsot:

Além disso, poliedros projectiva todos têm uma característica de Euler, correspondendo ao plano projetivo real, enquanto poliedros toroidal têm característica de Euler 0, correspondente ao toro .

Grafos planares

A característica de Euler pode ser definido para ligado grafos planares por a mesma fórmula como para superfícies poliédricas, onde f é o número de faces no gráfico, incluindo a face exterior.

A característica de Euler de qualquer gráfico planar é 2. Para via projeção estereográfica do plano mapeia para a esfera bidimensional, de tal forma que os mapas de gráfico para uma decomposição poligonal da esfera, que tem característica Euler 2. Este ponto de vista está implícito na prova de Cauchy da fórmula de Euler dada abaixo.

A prova da fórmula de Euler

Os primeiros passos da prova, no caso de um cubo

A primeira prova rigorosa da fórmula de Euler, dada por Cauchy em 1811, é como se segue.

Remover uma face da superfície poliédrica. Puxando as arestas da face ausente longe um do outro, deformar todo o resto em um gráfico planar de pontos e curvas, como ilustrado pela primeira das três gráficos para o caso especial de o cubo. (A suposição de que a superfície poliédrica é homeomorfo à esfera no início é o que torna isso possível.) Após esta deformação, as faces regulares geralmente não são regulares anymore. O número de arestas e vértices permaneceu a mesma, mas o número de faces foi reduzido por 1. Como tal, provando a fórmula de Euler para a poliedro reduz a provar V - E + F = 1, para isso, objecto planar deformado.

Se houver uma face com mais do que três lados, desenhar uma diagonal, isto é, uma curva através da face de ligação entre dois vértices, que ainda não estão conectados. Isso adiciona uma borda e um rosto e não altera o número de vértices, por isso não muda a quantidade V - E + F. Continue adicionando bordas desta maneira até que todas as faces são triangulares.

Aplicar repetidamente uma das duas transformações seguintes:

1. Remover um triângulo com apenas uma borda adjacente ao exterior, como ilustrado pelo segundo gráfico. Isto diminui o número de arestas e faces por um cada e não altera o número de vértices, de modo que preserva V - E + F.
2. Remover um triângulo com dois bordos compartilhados pelo exterior da rede, tal como ilustrado pelo terceiro gráfico. Cada triângulo remoção remove um vértice, duas bordas e um rosto, por isso preserva V - E + F.

Repita estes dois passos, um a seguir ao outro, até que apenas um triângulo permanece.

Neste ponto, o triângulo solitário tem V = 3, E = 3, e F = 1, de modo que V - E + F = 1. Uma vez que cada um dos dois passos de transformação acima conservados a essa quantidade, temos mostrado V - E + F = 1 para o deformado, planar objecto demonstrando assim V - e + f = 2 para o poliedro. Isto prova o teorema.

Para provas adicionais, consulte Dezenove As provas de fórmula de Euler por David Eppstein. Várias provas, incluindo suas falhas e limitações, são usados como exemplos Provas e Refutações por Imre Lakatos.

Definição topológica

As superfícies poliédricas discutidos acima são, em linguagem moderna, bidimensional finita CW-complexos. (Quando apenas faces triangulares são usados, eles são bidimensionais finita complexos simpliciais). Em geral, para qualquer finito CW-complexo, a característica de Euler pode ser definida como a soma alternada

onde k _n indica o número de células de dimensão n no complexo.

Mais ainda, geralmente, para qualquer espaço topológico, podemos definir o n th Betti número b _n como o Ranking do n -ésimo grupo de homologia singular. A característica de Euler pode então ser definida como a soma alternada

Esta quantidade está bem definido que os números de Betti são todos finita e que sejam zero para além de um certo índice n _0. Para os complexos simpliciais, esta não é a mesma definição como no parágrafo anterior, mas um cálculo da homologia mostra que as duas definições darão o mesmo valor para .

Propriedades

Como corolário Poincaré dualidade, a característica de Euler de qualquer colector odd-dimensional fechado é zero. Isto aplica-se mais geralmente a qualquer compacto espaço estratificada em que todos os estratos são impares-dimensional. Além disso, a característica de Euler se comporta bem no que se refere a muitas operações básicas sobre espaços topológicos, como se segue.

Invariância homotopia

Desde a homologia é um invariante topológico (na verdade, uma invariante homotopy - dois espaços topológicos que são equivalentes homotopy têm isomorphic grupos de homologia), por isso é a característica de Euler.

Por exemplo, qualquer poliedro convexo é homeomorfo para o tridimensional bola, de modo que a sua superfície é homeomorfos (daí homotopy equivalente) para o bidimensional esfera , que tem característica de Euler 2. Isto explica porque poliedros convexa tem característica de Euler 2.

Princípio da inclusão-exclusão

Se M e N são quaisquer dois espaços topológicos, em seguida, a característica de Euler da sua união disjunta é a soma de suas características de Euler, desde homologia é aditiva sob união disjunta:

De modo mais geral, se M e N são subespaços de um espaço maior X, em seguida, assim que são a sua união e intersecção. Em alguns casos, a característica de Euler obedece a uma versão do princípio da inclusão-exclusão:

Isto é verdade nos seguintes casos:

• Se M e N são uma excisiva casal. Em particular, se o interiores do M e N no interior do sindicato ainda cobrir o sindicato.

• Se X é um localmente espaço compacto e um usa características de Euler com compacto suportes, não são necessários pressupostos sobre M ou N.

• Se X é um espaço estratificada em que todos os estratos são ainda dimensional, o princípio da inclusão-exclusão é válida se M e N são sindicatos de estratos. Isto aplica-se, em particular, se M e N são subvariedades de um complexo variedade algébrica.

Em geral, o princípio da inclusão-exclusão é falsa. A contra-exemplo é dado pela tendo X ser a reta real, M um subconjunto que consiste em um ponto e N o complementar de M.

Propriedade do produto

Além disso, a característica de Euler de qualquer espaço do produto M × N é

Estas propriedades adição e multiplicação também são apreciados por cardinalidade de conjuntos . Deste modo, a característica de Euler pode ser visto como uma generalização de cardinalidade; ver .

Cobrindo espaços

Da mesma forma, para um k -sheeted cobrindo espaço tem um

De modo mais geral, para uma espaço cobertura ramificado, a característica de Euler da tampa pode ser calculado a partir do acima, com um factor de correcção para os pontos de ramificação, o qual produz o Fórmula de Riemann-Hurwitz.

Propriedade fibraç~ao

A propriedade do produto tem muito mais em geral, para fibrações com certas condições.

Se é um fibração com fibra F, com a base B caminho-ligado, e a fibração é orientável por um campo K, em seguida, a característica de Euler com coeficientes no campo K satisfaz a propriedade do produto:

Isso inclui espaços e produtos que cobrem espaços como casos especiais, e pode ser comprovado pela Sequência espectral Serre na homologia de uma fibração.

Para feixes de fibras, este também pode ser entendida em termos de um transferência mapa - Note que este é um levantamento e vai "o caminho errado" - cuja composição com o mapa de projeção é multiplicação pela Euler classe da fibra:

Relações com outros invariantes

A característica de Euler de uma fechado orientável superfície pode ser calculada a partir da sua genus g (o número de tori em um ligado decomposição soma da superfície; intuitivamente, o número de "alças") quanto

A característica de Euler de uma superfície não fechada orientável pode ser calculada a partir do seu género não orientável k (o número de planos projetivos reais em uma decomposição soma conectado da superfície) como

Para colectores lisas fechadas, a característica de Euler coincide com o número de Euler, isto é, o Euler de sua classe tangente feixe avaliada com classe fundamental de um colector. A classe de Euler, por sua vez, refere-se a todos os outros classes características de fibrados vetoriais.

Para fechada Variedades Riemannianas, a característica de Euler também pode ser encontrado através da integração da curvatura; ver o Gauss-Bonnet teorema para o caso bidimensional eo generalizada teorema de Gauss-Bonnet para o caso geral.

Um análogo discreto do teorema de Gauss-Bonnet é Teorema de Descartes que o "avaria total" de um poliedro , medido em círculos cheios, é a característica de Euler do poliedro; ver defeito (geometria).

O teorema de Hadwiger caracteriza a característica de Euler como o único ( até multiplicação escalar) Tradução invariante, finitamente aditivo, a função set não-necessariamente-não-negativo definido em uniões finitas de compacto convexo define em R ⁿ que é "homogênea de grau 0".

Exemplos

A característica de Euler pode ser facilmente calculado para superfícies gerais por encontrar um poligonalização da superfície (que é, uma descrição de um complexo-CW) e utilizando as definições acima.

Nome	Imagem	Euler característica
Intervalo		1
Círculo		0
Disco		1
Esfera		2
Toro (Produto de dois círculos)		0
Toro duplo		-2
Toro triplo		-4
Plano projetivo real		1
Fita de Möbius		0
Garrafa de Klein		0
Duas esferas (não ligado) (União Disjoint de duas esferas)		2 + 2 = 4
Três esferas (não ligado) (União Disjoint de três esferas)		2 + 2 + 2 = 6

Qualquer espaço contrátil (isto é, uma homotopia equivalente a um ponto) tem homologia trivial, o que significa que o número de Betti 0 é 1 e os outros 0. Portanto, sua característica de Euler é 1. Este caso inclui espaço euclidiano 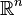de qualquer dimensão, bem como a unidade de bola sólida em qualquer espaço euclidiano - o intervalo unidimensional, o disco bidimensional, a bola tridimensional, etc.

O n-dimensional esfera tem o número 1 em Betti dimensões 0 e n, e todos os outros números de Betti 0. Daí a sua característica de Euler é - Ou seja, 0 ou 2.

O verdadeiro n -dimensional espaço projetivo é o quociente entre o n -sphere pelo mapa antípoda. Daí resulta que a sua característica de Euler que é exactamente metade da esfera correspondente - 0 ou 1.

O toro n-dimensional é o espaço do produto de n círculos. Sua característica Euler é 0, pela propriedade do produto. Quantas pentágonos e hexágonos que é preciso para fazer uma Bola de futebol? Suponha que usamos hexágonos e pentágonos; então temos enfrenta. Cada pentágono (hexágono) possui 5 vértices (6 vértices), e cada um é compartilhado entre três caras, daí temos vértices. Da mesma forma, cada pentágono (hexágono) tem 5 bordas (6 arestas), e cada um é compartilhado entre dois rostos, portanto, nós temos bordas.

Uma vez que a esfera tem característica de Euler 2, deve ser que . O resultado é que precisamos sempre de 12 pentágonos em uma bola de futebol / soccer; o número de hexágonos é, em princípio, sem restrições (mas para a / bola de futebol de futebol de verdade, obviamente, escolhe um número que faz com que a bola o mais esférico possível). Pode-se também aplicar este resultado ao fulerenos.

Generalizações

Para cada combinatória complexo de células, um define a característica de Euler como o número de 0-células, menos o número de células-1, mais o número de células-2, etc, se esta soma alternada é finito. Em particular, a característica de Euler de um conjunto finito é simplesmente a sua cardinalidade, e a característica de Euler de um gráfico é o número de vértices menos o número de arestas.

Mais geralmente, pode-se definir a característica de Euler de qualquer complexo de cadeia como sendo a soma do alternada fileiras dos grupos de homologia do complexo de cadeia.

Uma versão utilizada geometria algébrica é como se segue. Para qualquer maço em um projectiva esquema de X, um define a sua característica de Euler

onde é a dimensão da i-ésima grupo cohomology maço de .

Outra generalização do conceito da característica de Euler em variedades vem orbifolds. Enquanto cada variedade tem um número inteiro Euler característica, um orbifold pode ter uma característica de Euler fraccionada. Por exemplo, o orbifold lágrima tem característica de Euler 1 + 1 / p, em que p é um número primo que corresponde ao ângulo do cone 2 π / p.

O conceito da característica de Euler de um finito limitada poset é outra generalização, importante na análise combinatória . Um poset é "limitada" se ele tem maior eo menor dos elementos; chamam 0 e 1. A característica de Euler de tal CPO é definido como o número inteiro μ (0,1), em que μ é a Função de Möbius em que poset de álgebra incidência.

Isto pode ser mais generalizada, definindo um Q -valued característica de Euler para certos finito categorias, uma noção compatível com as características de Euler de gráficos, orbifolds e posets mencionados acima. Neste cenário, a característica de Euler de um finito grupo ou monóide G é 1 / | L |, e a característica de Euler de um finito grupóide é a soma de 1 / | G _i |, onde, escolhemos um grupo representativo G _i para cada componente conectado do grupóide.