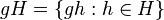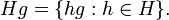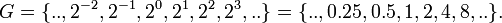Grupo (matemática)
Sobre este escolas selecção Wikipedia
Arranjar uma seleção Wikipedia para as escolas no mundo em desenvolvimento sem internet foi uma iniciativa da SOS Children. Antes de decidir sobre o patrocínio de uma criança, por que não aprender sobre as diferentes instituições de caridade de patrocínio primeiro ?

Um grupo é um dos objetos fundamentais de estudo no campo da matemática conhecido como álgebra abstrata . O ramo da álgebra que estuda grupos é chamado de teoria de grupos . A teoria do grupo tem inúmeras aplicações na matemática, ciência e engenharia. Muitas estruturas algébricas tais como campos e espaços vetoriais podem ser definidos de forma concisa em termos de grupos e teoria do grupo fornece uma importante ferramenta para estudar a simetria , uma vez que as simetrias de qualquer objeto formar um grupo. Grupos são, portanto, essenciais em abstrações ramos da física envolvendo simetria princípios, tais como a relatividade , mecânica quântica e física de partículas . Além disso, sua capacidade de representar geométricas transformações encontra aplicações em química , computação gráfica, e outros campos.
| A teoria do grupo |
|---|
Noções básicas
Homomorfismos de grupos
|
Grupos finitos
Classificação das finito grupos simples
Grupos de Mathieu
Grupos Conway
Grupos Janko
Grupos Fischer
|
Grupos modulares
|
Topológico / Grupos de Lie
Infinito grupo de Lie dimensional
|
Grupos algébricos |
Muitas estruturas investigadas em matemática vir a ser grupos. Estes incluem sistemas familiares número, tais como: os números inteiros , os números racionais , os números reais , e os números complexos sob disso, assim como os números racionais não-zero, reais e números complexos sob multiplicação. Outros exemplos importantes são os seguintes: o grupo de não-singulares matrizes sob a multiplicação, e o grupo de funções inversibles sob composição . A teoria do grupo permite que as propriedades de tais estruturas a serem investigados em uma configuração geral.
Definição
Um grupo (G *) é um definido G com um operação binária * que satisfaz a seguinte quatro axiomas:
- Encerramento: Para tudo a, b em G, o resultado de a * b também é expressa em g.
- Associativity : Para tudo a, b e c em L, (a * b) * c = a * (b * c).
- Elemento de identidade: Não existe um elemento e em G tal que para todo um em G, e * a = a * e = a.
- Elemento Inverso: Para cada um em G, existe um elemento b em G tal que a * b * b = A = E, onde E é um elemento de identidade.
Alguns textos omitir o requisito explícito de fecho, uma vez que o fechamento do grupo decorre da definição de um operação binária.
Usando a propriedade do elemento de identidade, pode ser mostrado que um grupo tem exatamente um elemento de identidade. Veja a prova abaixo.
O inverso de um elemento a também pode ser mostrado para ser único, e é geralmente escrito a -1 (mas veja a notação abaixo para grupos aditiva escritas).
Um grupo (G, *) é muitas vezes denotado simplesmente G, onde não existe qualquer ambiguidade quanto ao que a operação é.
Ilustração de definição

Um exemplo irá explicar algumas propriedades de grupos. Considere um quadrado . Estamos interessados em as simetrias da praça. Existem os seguintes tipos de simetrias:
- rotação de cerca de 90 °, 180 ° e 270 ° (sentido horário). Vamos escrever essas simetrias como podridão 90 °, 180 ° apodrecer, e apodrecer 270 °, respectivamente. Note-se que as rotações anti-horário são incluídos aqui, por exemplo, rotação de 270 ° no sentido horário é igual a rotação de 90 ° no sentido anti- horário.
- reflexão ao longo da linha média vertical ou horizontal, ou ao longo de dois diagonais. Vamos escrever as reflexões como ref V, ref H, ref D1 e D2 ref, respectivamente.
- Finalmente, o código de operação idêntica tudo deixando inalterada é também uma simetria.
Todos eles manter a forma do quadrado inalterada. (Nas imagens, os vértices são coloridas apenas para fazer claras as operações).
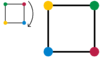 |  |  | 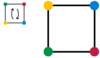 |  | 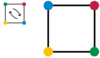 |  |
| Rotação no sentido horário em 90 ° apodrecer 90 ° | Rotação no sentido horário em 180 ° apodrecer 180 ° | Rotação no sentido horário por 270 ° apodrecer 270 ° | Reflexão ao longo da vertical ref V | Reflexão ao longo da ref horizontal H | Reflexão ao longo de uma diagonal ref D1 | Reflexão ao longo do outro ref diagonal D2 |
Este conjunto de simetrias L é um exemplo de um grupo, o chamado . grupo diedro de ordem 8 Sendo um grupo significa o seguinte:
- Dois simetrias pode ser composto, isto é, dada duas simetrias a e b, que podem realizar uma primeira e, em seguida, b e ainda o resultado será uma simetria. Nós escrevemos o resultado b * um (que significa "b após a"). Por exemplo, por rotação de 270 ° e, em seguida, por rotação de 180 ° é igual a uma rotação de 90 °, ou seja, utilizando os símbolos acima, temos
- apodrecer 180 ° * apodrecer 270 ° = apodrecer 90 °.
- Em uma linguagem mais formal, L é dotada de uma * operação binária, ou seja, quaisquer dois elementos podem ser compostos de um terceiro elemento.
Aplicado a este grupo exemplo, a definição lê:
- Associativity : dado três elementos a, b e c de G, (a * b) * c = a * (b * c).
- Elemento de identidade: Não existe um elemento e em G tal que para todo um em G, e * a = a * e = a. No exemplo, e é apenas o simetria tudo o que deixa inalterada.
- Elemento Inverso: Para cada um em G, existe um elemento b em G tal que a * b * b = A = E, onde E é um elemento de identidade. No exemplo, a rotação de um dado ângulo no sentido horário e, em seguida, girando pelo ângulo mesmo sentido anti-horário vai deixar a praça inalterado eo mesmo é verdade se inverter a ordem, ou seja, primeiro sentido anti-horário e, em seguida, no sentido horário. Além disso, o que reflecte ao longo da diagonal, por exemplo, pode ser invertida através da aplicação da mesma reflexão novamente. Em símbolos:
- rot 270 ° * apodrecer 90 ° = apodrecer 90 ° * apodrecer 270 ° = id e ref D1 * ref D1 = id.
História
Grupos de permutações já estavam sendo estudados no século 18 e foram aplicados para resolver problemas na teoria das equações. No entanto, a noção formal de um grupo não foi publicado até o final do século 19 , e por esta altura grupos tinham encontrado aplicações em teoria dos números , bem como em geometria .
Conceitos básicos em teoria dos grupos
Subgrupos
Um subconjunto H ⊂ G é chamada subgrupo se a restrição de * H é para um grupo de operação em H. Em outras palavras, é um grupo com a restrição de a operação definida em G. No exemplo acima, as rotações constituem um subgrupo, uma vez que uma rotação do composto com uma rotação continua a ser uma rotação.
O subgrupo de teste é uma condição necessária e suficiente para um subconjunto H de um grupo G que são um subgrupo: é suficiente verificar que g -1 h ∈ H para todos g, h ∈ H. O de fecho, sob o grupo de operação e inversão, de qualquer subconjunto não vazio de um grupo é um subgrupo.
Se L é um grupo finito, então também é H. Além disso, a fim de H divide a ordem de L ( Teorema de Lagrange).
Os poderes de qualquer elemento de um e suas inversas (que é, um 0 = E, A, A 2, A 3, A 4, ..., -1, -2, -3 um, um -4, ...) sempre formam um subgrupo de um grupo maior. Diz-se que um subgrupo que gera.
Um subgrupo H sempre define um conjunto de esquerda e direita cosets. Dado um elemento g arbitrário em G, a classe lateral esquerda da H contendo g é
eo coset direito de H contendo g é
O conjunto de classes laterais esquerdos do H forma uma partição dos elementos de G; isto é, duas classes laterais esquerda são iguais ou tem uma vazio interseção . O mesmo vale das classes laterais direita do H. Em geral, as classes laterais esquerdos de H não são necessariamente iguais às classes laterais direita de H. Se for o caso, que para todos g em L, gH = Hg, em seguida, H é dito ser um subgrupo normal.
Grupos de quociente
Se N é um subgrupo normal de G, seu conjunto de classes laterais esquerda e direita cosets são os mesmos e pode-se falar simplesmente do conjunto de classes laterais de N. Neste caso, o conjunto de classes laterais de N pode ser equipado com uma operação (algumas vezes chamado coset multiplicação, adição ou classe lateral) para formar um novo grupo, o chamado grupo quociente G / N. A operação entre as classes laterais se comporta da maneira mais agradável possível: (Ng) · (NH) = N (gh) para todo g e h em G. Nota-se que a classe lateral N serve como a identidade desse grupo, e o inverso de Ng no grupo quociente é (Ng)  = N (g
= N (g  ).
).
Grupos simples
Se um grupo G não é trivial do grupo e os seus subgrupos normais são apenas o grupo trivial e o próprio grupo, é chamado um grupo simples. Com o conceito de grupos quociente, que pode ser formulada de forma equivalente como: Um grupo com apenas o grupo trivial e o próprio grupo como grupos quociente é simples.
Homomorfismos de grupos
Se G e H são dois grupos, A grupo homomorphism f é um mapeamento f: G → H que preserva a estrutura dos grupos em causa. A estrutura dos grupos a ser determinado pela operação de grupo, isto significa o seguinte: se g e k são quaisquer dois elementos em L, em seguida
- f (gk) = f (g) f (k).
Este requisito assegura que f (1 L) = 1 H, e também f (g) -1 = f (-1 g) para todos g em L.
Dois grupos G e H são chamados isomorfos se existe um grupo f homomorphism entre G e H que é tanto surjective (sobre) e injetivo (um-para-um).
O um núcleo de f homomorphism é denotado ker f e é o conjunto de elementos em L, que são mapeados para a identidade em H. Isto é, ker f = {g em L: f (g) = 1 H}. O núcleo de um homomorfismo é sempre um subgrupo normal. O Primeiro Isomorfismo Teorema afirma que o imagem de um homomorfismo de grupos, f (G) é isomorfo ao grupo quociente G / ker f. Um fato úteis relativas homomorphisms é que eles são injective se e somente se seu kernel é trivial (ie ker f = {1} G).
Grupos abelianos
Um grupo  é dito ser abelian, ou comutativa, se a operação satisfaz a lei comutativa. Isto é, para todos
é dito ser abelian, ou comutativa, se a operação satisfaz a lei comutativa. Isto é, para todos  e
e 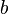 em
em  ,
,  . Se não, o grupo é chamado não-abeliano ou não-comutativa. O nome "abelian" vem do matemático norueguês Niels Abel. O exemplo acima de simetrias da praça é não-abeliano, porque
. Se não, o grupo é chamado não-abeliano ou não-comutativa. O nome "abelian" vem do matemático norueguês Niels Abel. O exemplo acima de simetrias da praça é não-abeliano, porque
- apodrecer 90 ° * ref = V ref D2 ≠ ref D1 = V ref * rot 90 °
O centro de um grupo é um subgrupo que consiste em os elementos que se deslocam com todos os outros elementos do grupo. Em um grupo conmutativo o centro é todo o grupo; No outro extremo, há grupos cujo centro é trivial, ou seja, consiste apenas no elemento de identidade.
Grupos cíclicos
Um grupo cíclico é um grupo cujos elementos podem ser gerado por sucessiva composição do grupo de operação a ser aplicada a um único elemento do referido grupo. Um elemento com essa propriedade é chamada um gerador ou um elemento primitivo do grupo. Grupos cíclicos são abelian.
Um grupo cíclico multiplicativo em que G é o grupo, e um é um gerador de:
Um grupo cíclico aditivo, com um gerador de:
Se a composição sucessiva da operação de definição do grupo é aplicado a um elemento não-primitivo do grupo, um subgrupo cíclico é gerado. Conforme O teorema de Lagrange, a ordem do subgrupo cíclico divide a ordem do grupo. Assim, se a ordem de um grupo finito é privilegiada , todos os seus elementos, excepto a identidade, são elementos primitivos do grupo.
Ordem dos grupos e elementos
O ordem de um grupo L, geralmente indicados por | L | ou, ocasionalmente, por o (G), é o número de elementos do conjunto L. Se a encomenda não é finito, então o grupo é um grupo infinito, denotada | G | = ∞.
A ordem de um elemento de um grupo de um L é o número inteiro positivo menos n tal que n = um de e, onde n representa um  , Ou seja, a aplicação da operação * de n cópias o valor um. (Se * representa multiplicação, então um n corresponde ao enésimo poder de um.) Se não existir tal n existe, em seguida, a fim de a é dito ser o infinito. A ordem de um elemento, é a mesma que a ordem do subgrupo cíclico gerado por esse elemento.
, Ou seja, a aplicação da operação * de n cópias o valor um. (Se * representa multiplicação, então um n corresponde ao enésimo poder de um.) Se não existir tal n existe, em seguida, a fim de a é dito ser o infinito. A ordem de um elemento, é a mesma que a ordem do subgrupo cíclico gerado por esse elemento.
A ordem do grupo de exemplo acima é de oito, a ordem de podridão 90 ° é quatro, porque rotativa 4 vezes em 90 ° não está mudando nada. A ordem dos elementos de reflexão ref V etc. é dois.
Notações e observações
Operação de grupo
Grupos pode utilizar a notação diferente dependendo do contexto e a operação de grupo.
- Grupos de aditivos usar + para denotar disso, e no sinal de menos - para denotar inversas. Por exemplo, a + (- a) = 0 em Z.
- Grupos multiplicativos usar *,
 Ou o símbolo mais geral "composição"
Ou o símbolo mais geral "composição"  para denotar multiplicação, e o sobrescrito -1 para denotar inversas. Por exemplo, a * a -1 = 1. É muito comum para soltar o * e apenas escrever aa -1 em vez disso.
para denotar multiplicação, e o sobrescrito -1 para denotar inversas. Por exemplo, a * a -1 = 1. É muito comum para soltar o * e apenas escrever aa -1 em vez disso. - Grupos de funções • usar para designar composição de função, eo expoente -1 para designar inversas. Por exemplo, g • g -1 = e. É muito comum para soltar a • e apenas escrever gg -1 em vez disso.
Omitir um símbolo para uma operação é geralmente aceitável, e deixa ao leitor a conhecer o contexto ea operação de grupo.
Ao definir grupos, é notação padrão para usar parênteses para definir o grupo e seu funcionamento. Por exemplo, (H, +) indica o grupo formado por H, com o conjunto de adição como operação de grupo. Para grupos como (Z n, +) e (F q *, *), o grupo multiplicativo de elementos diferentes de zero no campo finito F q, é comum para soltar os parênteses e a operação (uma vez que apenas uma operação faz com que essas definido em um grupo), tal como Z n e q F *. Também é correto para se referir a um grupo por seu identificador de conjunto, por exemplo, H ou 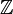 , Ou para definir o grupo de notação set-construtor, desde que fique claro qual grupo operação se destina.
, Ou para definir o grupo de notação set-construtor, desde que fique claro qual grupo operação se destina.
Elemento de identidade
Usando a propriedade do elemento de identidade, pode ser mostrado que um grupo tem exactamente um elemento de identidade. Por isso, um geralmente fala da identidade: suponha que tanto e e f são elementos de identidade. Então, porque é um f (à direita) e elemento de identidade * f = e, e porque e é uma (à esquerda) e elemento de identidade * f = f, de onde e = f.
O elemento de identidade e é, por vezes conhecido como o "elemento neutro", e é por vezes designado por algum outro símbolo, dependendo do grupo de:
- Em grupos multiplicativos, o elemento de identidade pode ser indicado por um.
- Em invertível grupos de matriz, o elemento de identidade é geralmente denotada por I ou Id.
- Em grupos de aditivos, o elemento de identidade pode ser denotado por 0.
- Em grupos de funções, o elemento de identidade geralmente é denotada por f 0.
Se S é um subconjunto de G e um elemento x de G, então, em notação multiplicativa, xs é o conjunto de todos os produtos {xs: s em S}; semelhante a notação Sx = {sx: s em S}; e por dois subconjuntos S e T de G, nós escrevemos ST para {r: s em S, t em T}. Em aditivo notação, escrevemos x + S, S + x, e S + T para os respectivos conjuntos (ver cosets).
Inverso
O inverso de um elemento a também pode ser mostrado para ser única, e é geralmente escrita ou um -1 - um, dependendo do contexto. Suponhamos que um dado l inversa e outro inverso r. Em seguida
- l = l * l * e = (a * r) = (l * a) * e * r = r = r.
Além disso, em caso de um grupo, que só conhecem b * A = E, em seguida, este é suficiente para concluir que b é o inverso de um elemento (uma vez que é garantido um inverso de dois lados de uma de existir, e, em seguida, b deve ser igual -lo). De modo semelhante a * b = E é suficiente para a mesma conclusão.
(No entanto, um conjunto com uma operação binária pode ter vários elementos de identidade esquerda ou muitos elementos de identidade direito, desde que não tem nada do tipo oposto: levar, por exemplo, em qualquer definir a operação definida por a * b = b, então qualquer elemento é um elemento de identidade esquerda, mas nenhum é um elemento de identidade direito Da mesma forma, em um monoid um elemento pode ter vários elementos inversos esquerda, desde que não tem elementos certos inversa (e vice-versa):. o conjunto de todos os mapas de um conjunto infinito para X em si é um monoid sob composição de função, em que cada mapa injective tem uma inversa esquerda, e cada mapa surjective tem uma inversa direita, mas nenhuma dessas inversas é único em geral. No entanto, se todos os elementos em um monoid ter uma inversa esquerda, o monóide pode ser demonstrado ser um grupo).
Associatividade
Para uma sequência de múltiplos factores numa dada ordem, pode-se formar um produto de várias maneiras diferentes, inserindo parênteses; No entanto, por várias aplicações da propriedade associativa, quaisquer dois destes pode ser mostrado para ser igual. Por esta razão, a expressão
- 1 * 2 * * ··· a n
é inequívoca e parênteses são geralmente omitida em tais expressões. Como conseqüência, quase nunca é necessário invocar explicitamente a propriedade associativa.
Variantes da definição
Algumas definições de um grupo usar condições aparentemente mais fracas para a identidade e os elementos inversos. Em vez de requerer um elemento de identidade de dois lados, pode-se requerer separadamente a existência de um elemento de identidade esquerda e direita, e da mesma forma pode requerer um separadamente a existência de uma esquerda e direita elementos inversos: em ambos os casos, os elementos de esquerda e direita pode ser demonstrou ser o mesmo (e cada um é único).
Exemplos de grupos
Os inteiros sob disso
O grupo provavelmente mais familiar é o grupo de números inteiros sob disso . Pode-se pensar os axiomas de um grupo que está sendo modelado sobre as propriedades dos números inteiros Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...} , em conjunto com a operação de grupo "+", indica que, como de costume, a adição. Os axiomas que ser verificados são:
- Encerramento: Se a e b são números inteiros, em seguida, a b + é um número inteiro.
- Associativity: Se a, b, e c são números inteiros, então (a + b) + c = a + (b + c).
- Elemento Identidade: 0 é um número inteiro e para qualquer número inteiro um, 0 + a = a + 0 = a.
- Elementos inversas: Se a é um número inteiro, então o número inteiro - um satisfaz as regras inversos: A + (- a) = (- A) + a = 0.
Este grupo também é abeliano porque a + b = b + a.
Se estendemos este exemplo ainda mais considerando os números inteiros com ambos adição e multiplicação, ele forma uma estrutura algébrica mais complicado chamado anel. (Mas, note que os números inteiros com multiplicações não são um grupo.)
Alguns grupos multiplicativos
O termo grupo multiplicativo refere-se a grupos cuja operação decorre de multiplicação , num certo sentido (dependendo do contexto).
Os inteiros sob multiplicação
Para começar, vamos dar um contra-exemplo: os números inteiros com a operação de multiplicação, denotado por "·". De acordo com a notação geral, este é denotado (Z, ·). Satisfaz os de fecho, associamento e identidade axiomas, mas não têm inversos: não é verdade que, sempre que a é um número inteiro, não é um número inteiro de tal modo que b ab = bA = 1. Por exemplo, a = 2, é um número inteiro, mas a única solução para a equação AB = 1 é, neste caso, b = 1/2. Não podemos escolher b = 1/2 1/2 porque não é um número inteiro. Uma vez que nem todos os elementos do ácido (Z, ·) tem um inverso (multiplicativo), (Z, ·) não é um grupo. É, no entanto, um conmutativo monóide, que é uma estrutura semelhante a um grupo, mas não necessita de elementos inversos.
Os números racionais diferentes de zero
O passo natural para remediar esta está considerando o conjunto de números racionais Q, o conjunto de todas as frações de inteiros a / b, onde a e b são inteiros e b é diferente de zero, e a operação de multiplicação, mais uma vez indicado por "·". Uma vez que o número racional 0 não tem um inverso multiplicativo, (Q, ·), como (Z, ·), não é um grupo.
No entanto, se em vez utilizar o conjunto de todos os números racionais Q diferente de zero \ {0}, então (Q \ {0}, ·) não formam um grupo abeliano. Na verdade, ao encerramento, associatividade e elemento de identidade axiomas são fáceis de verificar e acompanhar a partir das propriedades de inteiros (não perdemos encerramento removendo zero, porque o produto de dois números racionais diferentes de zero não é zero). Finalmente, o inverso de a / b é b / a, por conseguinte, o axioma do elemento inversa é satisfeito.
Assim como os números inteiros formar um anel, os números racionais formar a estrutura algébrica de um campo, permitindo as operações de adição, subtração, multiplicação e divisão.
Multiplicativos grupos cíclicos
Em (Q, ·), existem os subgrupos cíclicos
- L = {a n, n ∈ Z} ⊂ Q
onde n é um n-ésimo os exponenciações de o elemento primitivo de um grupo que. Por exemplo, se a é 2, então
Este grupo é um exemplo de um grupo abeliano livre Hierarquia de uma: a patente é um, porque L é gerado por um elemento (uma ou equivalentemente um -1) e a freeness refere-se ao facto de que nenhum as relações entre os poderes deste gerador ocorrer. Portanto, L, é isomorfo para o grupo de inteiros (com adição) introduzido acima.
Consindering o grupo
- {A n, n ∈ Z / m Z},
o módulo de m se liga o grupo em um conjunto finito com um conjunto não fraccionada dos elementos, uma vez que o inverso (e 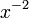 , Etc.) seria dentro do conjunto.
, Etc.) seria dentro do conjunto.
Os números inteiros diferentes de zero módulo um primo
As classes diferentes de zero de inteiros módulo p, um número primo , formam um grupo sob a multiplicação. O produto de dois números inteiros nenhum dos quais é divisível por p não é divisível por p ou (porque p é primo), que mostra que o conjunto indicado de classes é fechada sob a multiplicação. Associatividade é clara, ea classe de um é a identidade para a multiplicação, por isso continua a provar é que cada elemento tem uma inversa: dado um número inteiro a não divisível por p, tem de se encontrar um número inteiro b tal que
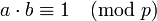 .
.
Isto pode ser demonstrado utilizando o Algoritmo de Euclides, por exemplo. Na verdade, neste exemplo é semelhante ao (Q \ {0}, ·) acima, porque acaba por ser o grupo de elementos diferentes de zero no finito campo F p. No entanto, é distintamente diferente do segundo grupo cíclico multiplicativo mencionado acima.
Grupos finitos
Se o número de elementos de um grupo G é finito, então a própria L é chamado um grupo finito. O de cima grupo diedro de ordem 8 é um exemplo. Duas classes importantes são os seguintes:
- os grupos (abelianos) cíclicos Z / n Z tratada acima. Qualquer grupo finito abeliano é um finito soma direta de grupos deste tipo, isso faz parte do teorema fundamental de grupos abelianos finitamente gerados.
- o grupo simétrico S N: é o grupo de permutações de n letras. Por exemplo, o grupo simétrico em 3 letras S 3 é o grupo que consiste de todas as permutas possíveis das três letras ABC, ou seja, contém os elementos de ABC, ACB, ..., até CBA, no total, seis (ou 3 factorial ) elementos. Paralelamente ao grupo de simetrias do quadrado acima, S 3 também pode ser interpretado como o grupo de simetrias de um triângulo equilátero.
O teorema de cayley declara que qualquer grupo finito (não necessariamente abeliano) pode ser expressa como um subgrupo de um grupo simétrico S N.
A teoria do grupo Elementary
A teoria do grupo Elementary se preocupa com fatos básicos que mantêm para todos os grupos individuais. Por exemplo:
- Você pode executar a divisão em grupos; ou seja, tendo em conta os elementos a e b do grupo G, existe exatamente uma solução em x G à equação x * a = b e exatamente uma solução y em G com a equação y = a * b. Na verdade, direita, respectivamente deixou multiplicação da equação por um -1 dá a solução x = b * a -1, respectivamente y = -1 * b.
- (meias e sapatos) O inverso de um produto é o produto dos inversos na ordem inversa: (a * b) -1 = -1 b * a -1.
- Prova: Iremos demonstrar que (a * b) * (b -1 * -1) = E, que, como mencionado acima é suficiente para provar que b -1 * -1 é o inverso de uma b *.
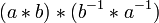
= 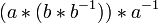
(Associatividade) = 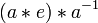
(Definição dos inversa) = 
(Definição de elemento neutro) = 
(Definição dos inversa)
A construção de novos grupos a partir de determinados queridos
Além subgrupos e grupos de quociente de duas maneiras básicas de construção de novos grupos a partir de determinados queridos. Outras técnicas de manipulação incluem:
- Produto directo: Se (L, *) e (H, •) são grupos, em seguida, o conjunto de L × H, juntamente com a operação (1 g, 1 h) (2 g, 2 h) = (1 g * g de 2, • h 1 h 2) é um grupo. O produto direto também pode ser definida com qualquer número de termos, finito ou infinito, usando a Produto cartesiano e definindo a operação coordenada-wise.
- Produto semidireto: Se N e H são grupos e φ: H → Aut (N) é um homomorphism grupo, em seguida, o produto semidireto de N e H em relação φ é o grupo (N × H, *), * com definido como
- (N 1, h 1) * (n = 2, H 2) = (n φ 1 (1 h) (n = 2), 2 h 1 h)
- Soma externo directo: A soma externo directo de uma família de grupos é o subgrupo do produto constituído por elementos que têm um número finito de coordenadas não-identidade. Se a família é finito a soma direta eo produto são equivalentes.
Generalizações
| Estruturas de grupo semelhante | |||||
| Totalidade * | Associatividade | Identidade | Inverses | Comutatividade | |
|---|---|---|---|---|---|
| Magma | Sim | Não | Não | Não | Não |
| Semigroup | Sim | Sim | Não | Não | Não |
| Monoid | Sim | Sim | Sim | Não | Não |
| Grupo | Sim | Sim | Sim | Sim | Não |
| Grupo Abelian | Sim | Sim | Sim | Sim | Sim |
| Laço | Sim | Não | Sim | Sim | Não |
| Quasigroup | Sim | Não | Não | Sim | Não |
| Grupóide | Não | Sim | Sim | Sim | Não |
| Categoria | Não | Sim | Sim | Não | Não |
| Semicategory | Não | Sim | Não | Não | Não |
| * Encerramento, que é usado em várias fontes para definir estruturas de grupo semelhante, é um axioma equivalente a totalidade, embora definida de forma diferente. | |||||
Em álgebra abstrata , as estruturas mais gerais surgem relaxando alguns dos axiomas que definem um grupo.
- Eliminando a exigência de que cada elemento tem uma inversa, então a estrutura algébrica resultante é chamada uma monoid.
- Um monóide sem uma identidade é chamado um semigroup.
- Alternativamente, relaxa o requisito de que a operação seja associativo enquanto ainda exige a possibilidade de divisão , a estrutura resultante é um algébrica loop.
- Um loop sem uma identidade é chamado um quasigroup.
- Finalmente, caindo todas axioma para a relação binária, a estrutura algébrica resultante é chamada uma magma.
Grupóides, que são semelhantes aos grupos, excepto que a composição de um b * não necessita de ser definido para toda a e b, surgem no estudo de tipos mais envolvidos de simetrias, muitas vezes em estruturas topológicos e analíticos. Grupóides, por sua vez, são os tipos especiais de categorias.
Supergrupos e Álgebras de Hopf são outras generalizações, e por isso são montes.
Grupos abelianos formar o protótipo para o conceito de um categoria abeliana, que tem aplicações para espaços vetoriais e além.
Leis formais do grupo está certo série de potências formal, que têm propriedades muito parecido com uma operação de grupo.
Em geometria diferencial , geometria algébrica e topologia , o conceito de grupo especializada para incluir grupos com estrutura adicional. Grupos de Lie, grupos algébricos e grupos topológicos são exemplos de grupo objetos:-estruturas de grupo como estar sentado em um categoria diferente da categoria normal dos conjuntos.