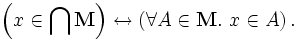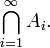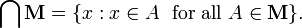Interseção (teoria dos conjuntos)
Fundo para as escolas Wikipédia
Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. patrocínio SOS Criança é legal!
Em matemática , a interseção de dois conjuntos A e B é o conjunto que contém todos os elementos de A que também pertencem a B (ou de modo equivalente, todos os elementos de B que também pertencem a a), mas não há outros elementos.
Para a explicação dos símbolos utilizados neste artigo, consulte o tabela de símbolos matemáticos.
Definição básica

A intersecção de A e B está escrito "A ∩ B". Formalmente:
- x é um elemento de um ∩ B se e apenas se
- x é um elemento de A e
- x é um elemento de B.
- Por exemplo:
- A intersecção dos conjuntos {1, 2, 3} e {2, 3, 4} é {2, 3}.
- O número 9 não está na interseção do conjunto de números primos {2, 3, 5, 7, 11, ...} eo conjunto de números ímpares {1, 3, 5, 7, 9, 11, ...}.
Se a interseção de dois conjuntos A e B está vazio, ou seja, eles não têm elementos em comum, em seguida, disse que estão a ser desmembrado, denotado: A ∩ B = Ø. Por exemplo, os conjuntos {1, 2} e {3, 4} são disjuntos, escrito
{1, 2} ∩ {3, 4} = O.
Mais geralmente, pode-se tomar a intersecção de vários conjuntos de uma só vez. A interseção de A, B, C, e D, por exemplo, é um ∩ B ∩ C ∩ D = A ∩ (B ∩ (C ∩ D)). Intersecção é uma associativo operação; Assim,
A ∩ (B ∩ C) = (A ∩ B) ∩ C.
Interseções arbitrárias
A noção mais geral é a interseção de uma coleção não vazia arbitrária de conjuntos. Se M for um conjunto não-vazio cujos elementos são eles próprios define, então x é um elemento de a interseção de M se e apenas se para cada elemento A de M, x é um elemento de um. Em símbolos:
Esta ideia subsume os parágrafos anteriores, em que, por exemplo, A C ∩ B ∩ é a interseção da coleção {A, B, C}.
A notação para este último conceito pode variar consideravelmente. Definir teóricos , por vezes, vai escrever "∩ M", enquanto outros, ao contrário, escrever "A ∩ ∈ M A". Esta última notação pode ser generalizada para "∩ i ∈ I A i", que se refere à interseção da coleção {A i: i ∈ I}. Aqui eu é um conjunto não vazio, e A i é um conjunto para cada i em I.
No caso em que o conjunto de índices que é o conjunto de números naturais , você pode ver a notação análoga à de um infinita série:
Quando a formatação é difícil, isso também pode ser escrito "A 1 A 2 ∩ ∩ ∩ A 3 ...", embora estritamente falando, A 1 ∩ (A 2 ∩ (A 3 ∩ ... não faz sentido. (Este último exemplo, um cruzamento de countably muitos jogos, é realmente muito comum, por exemplo ver o artigo sobre σ-álgebras.)
Finalmente, note-se que, sempre que o símbolo "∩" é colocado antes de outros símbolos em vez de entre eles, deve ser de um tamanho maior (⋂).
Intersecção Nullary
Note-se que na seção anterior foram excluídos os casos em que M foi o conjunto vazio (∅). A razão é como se segue. A intersecção da recolha M é definido como o conjunto (ver notação set-construtor)
Se M estiver vazia não existem conjuntos A em M, então a questão torna-se "qual x 's satisfaz a condição declarou?" A resposta parece ser cada possível x. Quando M é vazio a condição dada acima é um exemplo de um verdade vazia. Assim, a intersecção da família vazia deve ser o "conjunto de tudo". O problema é que não existe tal conjunto. Supondo que esse conjunto existe conduz a um problema famoso em teoria dos conjuntos ingênua conhecido como O paradoxo de Russell. Por esta razão, a interseção do conjunto vazio é deixado indefinido.
Uma correção parcial para este problema pode ser encontrada se nós concordamos em restringir a nossa atenção para os subconjuntos de um conjunto fixo chamado de U Universo. Neste caso, a intersecção de uma família de subconjuntos de U pode ser definida como
Agora, se M é vazio não há nenhum problema. A interseção é apenas todo o universo U, que é um bem definido definido por suposição.