Teoria de conjuntos

Teoria dos conjuntos é o ramo da matemática que estuda conjuntos, que são coleções de objetos. Embora qualquer tipo de objetos podem ser coletadas em um set, ajuste a teoria é aplicada na maioria das vezes para objetos que são relevantes para a matemática.

O estudo moderno da teoria dos conjuntos foi iniciado por Cantor e Dedekind na década de 1870. Após a descoberta de paradoxos na teoria dos conjuntos informal, foram propostos vários sistemas axioma no início do século XX, de que o Zermelo-Fraenkel axiomas, com o axioma da escolha, são os mais conhecidos.

A teoria dos conjuntos, formalizada usando lógica de primeira ordem , é o sistema mais comum fundamental para a matemática. A linguagem da teoria dos conjuntos é usado nas definições de quase todos os objetos matemáticos, como funções e conceitos da teoria dos conjuntos são integrados em todo o currículo de matemática. Fatos elementares sobre conjuntos e associação definido pode ser introduzido na escola primária, juntamente com os diagramas de Venn , para estudar coleções de objetos físicos comuns. Operações elementares, tais como união de conjunto e interseção podem ser estudadas neste contexto. Conceitos mais avançados, tais como cardinalidade são uma parte normal do currículo de matemática de graduação.

Além de seu uso como um sistema fundacional, teoria dos conjuntos é um ramo da matemática em seu próprio direito, com uma comunidade de pesquisa ativa. Pesquisa contemporânea em teoria conjunto inclui um conjunto diversificado de temas, que vão desde a estrutura do número real linha para o estudo da consistência da grandes cardeais.

História

Veja Johnson (1972) para um tratamento de livro de comprimento. Temas matemáticos normalmente surgem e evoluem através das interações entre muitos pesquisadores. O ponto de origem da teoria dos conjuntos é um pouco incomum em que ele pode ser identificado como um papel 1874 por Georg Cantor : "Em uma propriedade característica de todos os números reais algébricos".

Começando com o trabalho de Zeno em torno de 450 aC, os matemáticos tinham sido strugglinging com o conceito de infinito . Especialmente notável é o trabalho de Bernard Bolzano, na primeira metade do século 19. A compreensão moderna de infinito começou 1867-1871, com Georg Cantor trabalho 's em teoria dos números. Um encontro entre 1872 e Cantor Dedekind muito influenciado o pensamento de Cantor e culminou em Cantor (1874).

O trabalho de Cantor inicialmente polarizada os matemáticos de sua época. Enquanto Weierstrass e Dedekind suportado Cantor, Kronecker, agora visto como um dos fundadores da construtivismo matemático, não o fez. Mas a utilidade dos conceitos tais como cantoriana correspondência de um-para-um entre os sets, sua prova de que existem mais números reais do que números inteiros, ea "infinidade de infinidades" ("paraíso de Cantor") a operação conjunto de energia dá origem a, eventualmente levou à aceitação generalizada do cantoriana teoria dos conjuntos.

A próxima onda de excitação na teoria dos conjuntos veio por volta de 1900, quando se descobriu que cantoriana definir teoria deu origem a várias contradições, chamados antinomias ou paradoxos. Russell e Zermelo encontrou independentemente do paradoxo mais simples e mais conhecido, chamado agora O paradoxo de Russell e envolvendo "o conjunto de todos os conjuntos que não são membros de si mesmos." É evidente que este conjunto não pode ser um membro de si mesmo, e, portanto, deve ser um membro de si mesmo! Em 1899 Cantor tinha se colocou a questão: "qual é o número cardinal ? do conjunto de todos os conjuntos " e obteve um paradoxo relacionado. Foi mais tarde percebeu que esses paradoxos não são meramente teórico definido, e que na lógica da frase "esta sentença é falsa" dá origem a um problema semelhante, pois se a sentença é verdadeira, ela deve ser falsa. Kurt Gödel usado este fato em 1931 prova de sua célebre teorema da incompletude.

O impulso da teoria dos conjuntos era tal que o debate sobre os paradoxos não levou ao seu abandono. O trabalho de Zermelo em 1908 e Fraenkel em 1922 resultou na canônica teoria dos conjuntos axiomática ZFC, que é livre de paradoxos. O trabalho de analistas, tal como Lebesgue demonstrou a grande utilidade matemática da teoria dos conjuntos. teoria dos conjuntos axiomática tornou-se tecida no próprio tecido da matemática como a conhecemos hoje.

Conceitos básicos

A relação básica entre objetos e conjuntos é a associação ou relação "elementhood"; O dado um objeto e um conjunto A, ou O é um membro de A ou não é um membro. A relação básica entre dois conjuntos é o subconjunto relação, também chamado de inclusão set. Por exemplo, {a, b} é um subconjunto de {a, b, c}, mas {a, d} não é.

Assim como existem operações aritméticas que operam em números, há operações em teoria dos conjuntos que operam em conjuntos. Por exemplo, começando com os conjuntos {1, 2, 3} e {2, 3, 4}, a operação de união produz um novo conjunto {1, 2, 3, 4} que contém todos os elementos que estão em ambos os conjuntos, ea intersecção operação produz o conjunto {2, 3} que consiste em todos os elementos que estão em ambos os conjuntos originais. Operações adicionais sobre conjuntos incluem:

• Complementação: o conjunto de todos os elementos de um conjunto U que não estão em um conjunto A é chamado o complemento de A em relação a U, denotada . Esta terminologia é usado na maioria das vezes, quando L é um implict conjunto "universal", como no estudo de diagramas de Venn . O conjunto de elementos de U não em A também é chamado a diferença de conjunto, denotada .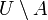
• O diferença simétrica de dois conjuntos consiste em todos os elementos que estão em exactamente um dos dois conjuntos.
• O Produto cartesiano de dois conjuntos A e B é composto por todos os pares ordenados (a, b), onde um é membro de A e b é um membro da B.
• O powerset de um conjunto A é constituída por todos os subconjuntos de A. Por exemplo, o powerset de {1, 2} é {{}, {1}, {2}, {1,2}}.

Interpretações

A idéia-chave na teoria dos conjuntos é a von Neumann universo de conjuntos puros. Um conjunto é puro, se todos os seus membros são conjuntos, todos os membros dos seus membros sejam sets, e assim por diante. Por exemplo, o conjunto que contém apenas o conjunto vazio é um conjunto não vazio puro. É comum na teoria dos conjuntos para restringir a atenção para os conjuntos puros, ao invés de estudar conjuntos arbitrários, e muitos sistemas axiomáticos da teoria dos conjuntos são destinados apenas para axiomatizar os conjuntos puros.

Os conjuntos puros estão dispostos na hierarquia cumulativa com base em quão profundamente os seus membros, membros de membros, etc. são aninhados. Cada conjunto é atribuído um número ordinal α nesta hierarquia, conhecida como o seu valor. Por outro lado, para cada ordinal α _α o conjunto V é definido para conter todos os conjuntos que são atribuídos classificação não superior a α. A atribuição de fileiras é feito por recursão transfinita: se o menor limite superior nas fileiras dos elementos de um conjunto X é α α Ranking então X é atribuído + 1.

Teoria dos conjuntos axiomática

Os conceitos básicos da teoria dos conjuntos pode ser estudada de maneira informal e intuitiva, em vez de axiomaticamente. Daí a teoria dos conjuntos muito elementar pode ser ensinado nas escolas primárias utilizando, por exemplo, diagramas de Venn . Esta abordagem intuitiva dá origem a antinomias, o mais simples e mais conhecido dos quais o ser Paradoxo. Russell da teoria dos conjuntos axiomática foi originalmente concebido para banir essas antinomias.

Os mais amplamente estudados sistemas da teoria dos conjuntos são baseadas no conceito de um hierarquia cumulativa de conjuntos. Tais sistemas são de dois tipos, aqueles cuja ontologia consiste de:

• Define sozinho. Isso inclui a teoria dos conjuntos axiomática mais comum, Zermelo-Fraenkel (ZFC), que inclui o axioma da escolha. Fragmentos de ZFE incluem:
  • Zermelo teoria dos conjuntos, que substitui o esquema axioma da substituição com a de separação;
  • Teoria dos conjuntos geral, um pequeno fragmento de Zermelo definir teoria suficiente para a Axiomas de Peano e conjuntos finitos;
  • Kripke-Platek teoria dos conjuntos, que omite os axiomas da infinidade, powerset, e escolha, e enfraquece os esquemas axioma da separação e substituição.
• Classes próprias, bem como conjuntos. Isso inclui Von Neumann-Bernays-Gödel teoria dos conjuntos, a qual tem a mesma força ZFC para teoremas sobre conjuntos por si só, e Morse-Kelley teoria dos conjuntos, que é mais forte do que ZFC.

Os sistemas NFU (com urelements) e NF (faltando-lhes) não são baseados em uma hierarquia cumulativa. NF e NFU incluem um "conjunto de todos os conjuntos", em relação à qual cada conjunto tem um complemento. Por outro lado, NF (mas não NFU) permite que os sistemas de jogos para os quais o axioma da escolha não se sustenta.

Sistemas de teoria dos conjuntos construtiva, como CST, czf, e IZF, incorporar seus axiomas em conjunto lógica intuicionista em vez de lógica de primeira ordem . No entanto, outros sistemas padrão aceitar a lógica de primeira ordem , mas apresentam uma relação filiação fora do padrão. Estes incluem teoria dos conjuntos rústica e teoria dos conjuntos fuzzy, em que o valor de um fórmula atômica que contém a relação de membros não é simplesmente verdadeiro e falso. O Modelos com valor de boolean de ZFC são um assunto relacionado.

Aplicações

Quase todos os conceitos matemáticos são agora definidos formalmente em termos de conjuntos e definir conceitos teóricos. Por exemplo, estruturas matemáticas tão diversos como gráficos, manifolds , anéis e espaços vetoriais são todos definidos como conjuntos que têm diversas (axiomáticas) propriedades. Equivalência e relações de ordem são onipresentes em matemática, com a teoria da relações é inteiramente fundamentada na teoria dos conjuntos.

Teoria dos conjuntos é também um sistema fundacional promissor para grande parte da matemática. Desde a publicação do primeiro volume de Principia Mathematica, que tem sido afirmado que a maioria ou mesmo todos os teoremas matemáticos podem ser obtidos utilizando um conjunto apropriadamente projetado de axiomas para a teoria dos conjuntos, aumentada com muitas definições, usando em primeiro ou segundo a lógica da ordem. Por exemplo, propriedades dos naturais e números reais podem ser obtidos dentro de teoria dos conjuntos, como cada sistema numérico pode ser identificado com um conjunto de classes de equivalência sob uma adequada relação de equivalência cujo campo é algum conjunto infinito.

Definir teoria como base para a análise matemática , topologia , álgebra abstrata , e matemática discreta também é incontroverso; matemáticos aceitar que (em princípio) teoremas nessas áreas podem ser derivadas das definições relevantes e os axiomas da teoria dos conjuntos. Poucos derivações completas de teoremas matemáticos complexos a partir de teoria dos conjuntos que tenham sido formalmente verificado, no entanto, porque tais derivações formais são muitas vezes muito mais do que a linguagem natural impermeabiliza matemáticos comumente presentes. Um projeto de verificação, Metamath, inclui derivações de mais de 10.000 a partir de teoremas Axiomas ZFC e usando lógica de primeira ordem .

As áreas de estudo

Teoria dos conjuntos é uma importante área de pesquisa em matemática, com muitos subcampos inter-relacionados.

Teoria dos conjuntos combinatória

Teoria dos conjuntos combinatória diz respeito a extensões de finitos combinatória para conjuntos infinitos. Isso inclui o estudo da aritmética cardinal eo estudo das extensões de O teorema de Ramsey, tais como o Erdos-Rado teorema.

Teoria dos conjuntos descritivo

Teoria dos conjuntos descritivo é o estudo de sub-grupos da linha real e, mais geralmente, subconjuntos de Espaços polonês. Ela começa com o estudo da no pointclasses Borel hierarquia e estende-se para o estudo de hierarquias mais complexos, tais como o hierarquia projetiva ea Wadge hierarquia. Muitas propriedades dos conjuntos de Borel pode ser estabelecido em ZFC, mas provar estas propriedades segure por conjuntos mais complicados requer axiomas adicionais relacionadas com determinacy e grandes cardeais.

O campo de teoria dos conjuntos descritivo eficaz é entre teoria dos conjuntos e teoria da recursão. Ele inclui o estudo de pointclasses lightface, e está intimamente relacionado com teoria hyperarithmetical. Em muitos casos, os resultados da teoria dos conjuntos descritiva clássica têm versões eficazes; em alguns casos, os novos resultados são obtidos por provar a versão eficaz em primeiro lugar e, em seguida, estendendo-se ("relativizar") para torná-lo mais amplamente aplicável.

Uma área recente de preocupações de investigação Borel relações de equivalência e definíveis mais complicadas relações de equivalência . Isto tem importantes aplicações para o estudo de invariantes em muitos campos da matemática.

Teoria dos conjuntos fuzzy

Na teoria dos conjuntos como Cantor definido e Zermelo e Fraenkel axiomatizada, um objeto é ou um membro de um conjunto ou não. Em teoria dos conjuntos fuzzy esta condição foi descontraído Zadeh assim que um objeto tem um grau de pertinência em um conjunto, como número entre 0 e 1. Por exemplo, o grau de pertinência de uma pessoa no set de "pessoas altas" é mais flexível do que um simples sim ou não como resposta e pode ser um número real tal como 0,75.

Teoria do modelo interno

Um modelo interno de Zermelo-Fraenkel (ZF) é um transitivo classe que inclui todos os ordinais e satisfaz todos os axiomas de ZF. O exemplo canônico é a constructible universo L desenvolvido por Gödel. O estudo de modelos interiores das extensões de ZF é de interesse na teoria dos conjuntos porque pode ser usado para provar resultados consistentes. Por exemplo, pode-se mostrar que, independentemente se um modelo V da ZF satisfaz o hipótese do contínuo ou o axioma da escolha, o modelo L interior construído dentro do modelo original irá satisfazer tanto a hipótese do contínuo e o axioma da escolha. Assim, a suposição de que é consistente ZF (tem qualquer modelo que seja) implica que ZF em conjunto com estes dois princípios é consistente.

O estudo de modelos internos é comum no estudo de determinação e grandes cardeais, especialmente quando se considera axiomas como o axioma de determinação que contradiz o axioma da escolha. Mesmo que um modelo fixo da teoria dos conjuntos satisfaz o axioma da escolha, é possível para um modelo interno para deixar de satisfazer o axioma da escolha. Por exemplo, a existência de grandes suficientemente cardeais implica que há um modelo interno satisfazendo o axioma de determinação (e, portanto, não satisfazem o axioma da escolha).

Grandes cardeais

Um grande cardeal é um número cardinal com uma propriedade extra. Muitos de tais propriedades são estudados, incluindo cardeais inacessíveis, Cardeais mensuráveis, e muitos mais. Estas propriedades normalmente implicam o número cardeal deve ser muito grande, com a existência de um cardeal com a propriedade especificada unprovable em Zermelo-Fraenkel.

Determinacy

Determinacy refere-se ao fato de que, sob os pressupostos adequados, determinados jogos de dois jogadores de informação perfeita são determinados desde o início no sentido de que um jogador deve ter uma estratégia vencedora. A existência dessas estratégias tem conseqüências importantes na teoria descritiva dos conjuntos, como a suposição de que uma classe mais ampla de jogos é determinada muitas vezes implica que uma classe mais ampla de conjuntos terão uma propriedade topológica. O axioma de determinação (AD) é um importante objeto de estudo; embora seja incompatível com o axioma da escolha, AD implica que todos os subgrupos da linha real são bem comportados (em particular, mensuráveis e com a propriedade conjunto perfeito). AD pode ser usado para provar que a Graus Wadge têm uma elegante estrutura.

Forçando

Paul Cohen inventaram forçando enquanto procura por uma modelo de ZFE em que o hipótese do contínuo falhar. Forçando adjacente a algumas determinado modelo da teoria dos conjuntos conjuntos adicionais, a fim de criar um modelo maior, com propriedades determinadas pela construção e do modelo original. Por exemplo, a construção de Cohen é contíguo subconjuntos adicionais dos números naturais , sem alterar qualquer um dos números cardinais do modelo original. Forçando é também um dos dois métodos para provar relativa consistência por métodos finitistic, o outro método sendo Modelos com valor de boolean.

Invariantes cardinais

A invariante cardeal é uma propriedade da linha verdadeira medida por um número cardinal. Por exemplo, uma invariante bem estudado é a menor cardinalidade de uma coleção de conjuntos parcos de reais cuja união é toda a linha real. Estes são invariantes no sentido de que quaisquer dois modelos isomórficos da teoria dos conjuntos deve dar o mesmo cardeal para cada invariante. Muitos invariantes cardinais foram estudados, e as relações entre eles são muitas vezes complexas e relacionadas com axiomas da teoria dos conjuntos.

Topologia de set-theoretic

Set-teóricas estudos topologia questões de topologia geral que são set-teórica na natureza ou que requerem métodos da teoria dos conjuntos avançados para a sua solução. Muitos desses teoremas são independentes de ZFC, exigindo axiomas mais fortes para a sua prova. Um problema é o famoso Pergunta espaço normal Moore, uma pergunta em topologia geral que foi objecto de intensa investigação. A resposta para a pergunta Moore espaço normal foi eventualmente provou ser independente de ZFC.

Objeções à teoria dos conjuntos

Desde a sua criação, tem havido alguns matemáticos que têm opôs-se usando a teoria dos conjuntos como uma fundação para a matemática, afirmando que é apenas um jogo que inclui elementos de fantasia. Errett Bispo demitido teoria dos conjuntos como " Deus matemática 's, que devemos deixar que Deus faça. " Também Ludwig Wittgenstein questionou especialmente a manipulação de infinidades, que diz respeito também ZF. Visões de Wittgenstein sobre fundamentos da matemática foram criticadas por Paul Bernays, e estreitamente investigado por Crispin Wright, entre outros.

A objeção mais freqüente para definir teoria é a visão construtivista de que a matemática é vagamente relacionadas à computação e que teoria dos conjuntos ingênua está sendo formalizada com a adição de elementos noncomputational.

Topos teoria tem sido proposto como uma alternativa à teoria dos conjuntos axiomática tradicional. Topos teoria pode ser usado para interpretar várias alternativas à teoria dos conjuntos, tais como construtivismo, a teoria conjunto finito, e teoria dos conjuntos computável.