Set (matemática)

Um conjunto é uma coleção de objetos distintos considerados como um todo. Os conjuntos são um dos mais fundamentais conceitos em matemática . O estudo da estrutura de conjuntos, teoria definida , é rica e contínua. Tendo sido só inventou no final do século 19 , a teoria dos conjuntos é agora uma parte onipresente da educação matemática, sendo introduzida a partir de escola primária em muitos países. Definir teoria pode ser visto como uma base a partir da qual a quase totalidade da matemática pode ser derivada.

Em filosofia , conjuntos são normalmente considerados objetos abstratos da físicas sinais de que são, por exemplo; três copos em uma mesa quando se fala de conjunto, como "os copos", ou as linhas de giz em uma placa na forma de abertura e fechamento colchete símbolos, juntamente com quaisquer outros símbolos entre os dois símbolos de suporte. No entanto, os defensores da realismo matemático incluindo Penelope Maddy argumentaram que conjuntos são objetos concretos.

A intersecção de dois conjuntos é composta dos objectos contidos em ambos os conjuntos, mostrado num diagrama de Venn .

Definição

No início de sua der Beiträge zur Begründung transfiniten Mengenlehre, Georg Cantor , o principal criador da teoria dos conjuntos, deu a seguinte definição de um conjunto:

Por um "set" queremos dizer qualquer coleção M em um todo de definidos, distintos objetos m (que são chamados os "elementos" de M) de nossa percepção [Anschauung] ou de nosso pensamento.

O elementos de um conjunto, também chamados de seus membros, pode ser qualquer coisa: números, pessoas, letras do alfabeto, outros conjuntos, e assim por diante. Os conjuntos são convencionalmente denotadas com maiúsculas. A instrução que define A e B são iguais significa que eles têm precisamente os mesmos membros (ou seja, todos os membros de A é também membro do B e vice-versa).

Ao contrário de um multiset, cada elemento de um conjunto deve ser exclusivo; há dois membros podem ser idênticas. Todas as operações de conjunto preservar a propriedade de que cada elemento do conjunto é único. A ordem em que os elementos de um conjunto estão listadas é irrelevante, ao contrário de uma sequência ou tupla.

Conjuntos descrevendo

Há duas maneiras de descrever, ou que especifique os membros da, um conjunto. Uma maneira é por definição intensional, usando uma regra ou descrição semântica. Veja este exemplo:

Um é o conjunto cujos membros são os primeiros quatro positivos inteiros .

B é o conjunto de cores do Bandeira francesa.

A segunda maneira é por extensão, isto é, listando cada membro do conjunto. Um definição extensional é simbolizada colocando a lista de membros em cintas:

C = {4, 2, 1, 3}

D = {azul, branco, vermelho}

A ordem em que os elementos de um conjunto estão listadas em uma definição extensional é irrelevante, assim como quaisquer repetições na lista. Por exemplo,

{6, 11} = {11, 6} = {11, 11, 6, 11}

são equivalentes, porque a especificação extensional significa apenas que cada um dos elementos mencionados é um membro do conjunto.

Para conjuntos com muitos elementos, a enumeração de membros pode ser abreviado. Por exemplo, o conjunto dos primeiros mil números inteiros positivos pode ser especificado como extensionalmente:

{1, 2, 3, ..., 1000},

onde o reticências ("...") indica que a lista continua de forma óbvia. Elipses também pode ser utilizado quando conjuntos têm infinitamente muitos membros. Assim, o conjunto de positivo mesmo números pode ser escrito como {2, 4, 6, 8, ...}.

A notação com o aparelho também pode ser utilizado numa especificação intencional de um conjunto. Neste uso, as chaves têm o significado "o conjunto de tudo ..." Então, E = {ternos de jogo de cartão} é o conjunto cujos quatro membros são ♠, ♦, ♥, e ♣. Uma forma mais geral do presente é notação set-construtor, através do qual, por exemplo, o conjunto F dos vinte números inteiros menores que são menos do que quatro quadrados perfeitos pode ser denotado:

F = {n ^2-4: n é um número inteiro; e 0 ≤ n ≤ 19}

Neste formato, o pontos (":") significa "de tal modo que", bem como a descrição pode ser interpretado como "F é o conjunto de todos os números da forma n ^2-4, de tal modo que n é um número inteiro no intervalo de 0 a 19 inclusive . " Às vezes o barra vertical ("|") é usado em vez do cólon.

Um muitas vezes tem a opção de especificar um conjunto intensionalmente ou extensionalmente. Nos exemplos acima, por exemplo, A = B = C e D.

Afiliação

Se algo é ou não é um elemento de um conjunto particular, então este é simbolizado por ∈ e ∉ respectivamente. Assim, no que diz respeito aos conjuntos acima definidos:

• 4 ∈ A e 285 ∈ F (desde 285 = 17² - 4); mas
• 9 ∉ F e verde ∉ B.

Cardinalidade

A cardinalidade | S | de um conjunto S é ". O número de membros de S" Por exemplo, uma vez que a bandeira francesa tem três cores, | B | = 3.

Há um conjunto sem membros e de zero cardinalidade, que é chamado de conjunto vazio (ou o conjunto nulo) e é representada pelo símbolo ø. Por exemplo, o conjunto A de todos os quadrados de três lados tem zero membros (| A | = 0), e, assim, um = O. Embora, como o número zero , pode parecer trivial, o conjunto vazio é muito importante em matemática. A existência deste conjunto é um dos conceitos fundamentais da teoria dos conjuntos axiomática .

Alguns conjuntos têm infinito cardinalidade. O conjunto N de números naturais , por exemplo, é infinito. Alguns cardinalities infinitas são maiores do que outros. Por exemplo, o conjunto de números reais tem maior cardinalidade do que o conjunto dos números naturais. No entanto, se puder ser demonstrado que a cardinalidade de (ou seja, o número de pontos em) uma linha recta é a mesma que a de qualquer cardinalidade segmento de linha que, de um inteiro avião, e de fato de qualquer espaço euclidiano .

Subconjuntos

Se todos os membros do conjunto A é também um membro do conjunto B, então A é dito ser um subconjunto de B, escrito (Também pronunciado A está contido em B). Equivalentemente, podemos escrever 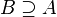, Lido como B é um superconjunto de A, B inclui A, ou B contém Um. A relação entre conjuntos estabelecidos pela é chamado de inclusão ou de contenção.

Se A é um subconjunto de, mas não igual a, B, então A é chamado um subconjunto apropriado de B, escrito (A é um subconjunto apropriado de B) ou (B é super adequada de A).

Note-se que as expressões e são usados de forma diferente por diferentes autores; alguns autores usam para significar o mesmo que (Respectivamente ), Ao passo que outros usam para significar o mesmo que (Respectivamente ).

A é um subconjunto de B

Exemplo:

• O conjunto de todos os homens é um subconjunto próprio do conjunto de todas as pessoas.
• 
• 

O conjunto vazio é um subconjunto de cada jogo e cada conjunto é um subconjunto de si mesmo:

Conjunto de energia

O conjunto de um conjunto S de energia pode ser definida como o conjunto de todos os subconjuntos de S. Isto inclui os subconjuntos formados a partir dos membros de S e o conjunto vazio. Se um conjunto finito S tem cardinalidade n, em seguida, o conjunto de S poder tem cardinalidade 2 ^n. Se S for um infinito (ou contável ou incontável) definir, em seguida, o conjunto de S poder é sempre incontável. O conjunto de potência pode ser escrito como 2 ^S.

Como um exemplo, o poder definir 2 ^{{1, 2, 3}} de {1, 2, 3} é igual ao conjunto {{1, 2, 3}, {1, 2}, {1, 3}, { 2, 3}, {1}, {2}, {3}, O}. A cardinalidade do conjunto original é 3, e o cardinal do conjunto de potência é 2 ³ ou 8. Esta relação é uma das razões para o conjunto de energia terminologia. Da mesma forma, a sua notação é um exemplo de uma convenção geral fornecer notações para conjuntos com base em suas cardinalities.

Conjuntos especiais

Existem alguns conjuntos que possuem grande importância matemática e são referidas com tal regularidade que adquiriram nomes especiais e as convenções de notação para identificá-los. Um destes é o conjunto vazio. Muitos destes conjuntos são representados usando Negrito Blackboard. Conjuntos de números especiais incluem:

• , Denotando o conjunto de todos os números primos .
• , Denotando o conjunto de todos os números naturais . Isto quer dizer, = {1, 2, 3, ...}, ou, por vezes, = {0, 1, 2, 3, ...}.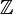
• , Denotando o conjunto de todos os números inteiros (seja positivo, negativo ou zero). Assim 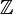= {..., -2, -1, 0, 1, 2, ...}.
• , Denotando o conjunto de todos os números racionais (isto é, o conjunto de todas as apropriadas e fracções impróprias ). Assim, . Por exemplo, e . Todos os números inteiros são neste conjunto uma vez que cada um número inteiro pode ser expressa como a fracção .
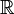• , Denotando o conjunto de todos os números reais . Este conjunto inclui todos os números racionais, juntamente com todos os irracionais números (ou seja, números que não podem ser reescritos como frações, tais como e √2).
• , Denotando o conjunto de todos os números complexos .

Cada um destes conjuntos de números tem um número infinito de elementos, e . Os números primos são utilizados com menos frequência do que os outros fora de teoria dos números e áreas afins.

Operações básicas

Sindicatos

Existem maneiras de construir novos conjuntos partir dos já existentes. Dois conjuntos podem ser "adicionado" juntos. A união de A e B, denotado por A ∪ B, é o conjunto de todas as coisas que são membros de A ou B.

A união de A e B

Exemplos:

• {1, 2} ∪ {vermelho, branco} = {1, 2, vermelho, branco}
• {1, 2, verde} ∪ {vermelho, branco, verde} = {1, 2, vermelho, branco, verde}
• {1, 2} ∪ {1, 2} = {1, 2}

Algumas propriedades básicas dos sindicatos são:

• A ∪ B = B ∪ A
• A ⊆ (A ∪ B)
• A ∪ A = A
• A ∪ ø = A
• A ⊆ B Se e apenas se A ∪ B = B

Interseções

Um novo conjunto também podem ser construídos por determinação de quais os membros de dois conjuntos têm "em comum". A intersecção de A e B, denotado por A ∩ B, é o conjunto de todas as coisas que são membros de ambos A e B. Se A ∩ B = O, então A e B são disse a ser separado.

A intersecção de A e B

Exemplos:

• {1, 2} ∩ {vermelho, branco} = O
• {1, 2, verde} ∩ {vermelho, branco, verde} = {verde}
• {1, 2} ∩ {1, 2} = {1, 2}

Algumas propriedades básicas de cruzamentos:

• A ∩ B = B ∩ A
• A ∩ B ⊆ A
• A ∩ A = A
• A ∩ O = O
• A ⊆ B Se e apenas se A ∩ B = A

Complementos

Dois conjuntos também podem ser "subtraídos". O complemento relativo de A em B (também chamada a diferença teórica definida de B e A), denotada por B \ A (ou B - A) é o conjunto de todos os elementos que são membros de B, mas não em membros de uma. Note que é válido para "subtrair" membros de um conjunto que não estão no conjunto, como remover verde de {1,2,3}; fazendo assim não tem nenhum efeito.

Em certas configurações de todos os conjuntos em discussão são considerados como sendo subconjuntos de um dado universal definido U. Em tais casos, L \ A, é chamado o complemento absoluta ou simplesmente complementar de A, e é indicado por A '.

O complemento relativo
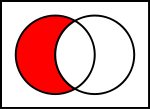
de A em B

O complemento de A em U

Exemplos:

• {1, 2} \ {vermelho, branco} = {1, 2}
• {1, 2, verde} \ {vermelho, branco, verde} = {1, 2}
• {1, 2} \ {1, 2} = ∅
• Se U é o conjunto de números inteiros, E é o conjunto de inteiros pares, e O é o conjunto de números inteiros ímpares, então o complemento de E na U é O, ou equivalentemente, E '= O.

Algumas propriedades básicas de complementos:

• Um ∪ A '= L
• A ∩ A '= ∅
• (A ')' = A
• A \ A = ∅
• A \ B = A ∩ B '

Produto cartesiano

Um novo conjunto pode ser construída associando cada elemento de um conjunto com todos os elementos do outro conjunto. O produto cartesiano de dois conjuntos A e B, denotado por A × B é o conjunto de tudo pares ordenados (a, b) de tal modo que um é um membro de a e b é um membro de B.

Exemplos:

• {1, 2} × {vermelho, branco} = {(1, vermelho), (1, branco), (2, vermelho), (2, branco)}
• {1, 2, verde} × {vermelho, branco, verde} = {(1, vermelho), (1, branco), (1, verde), (2, vermelho), (2, branco), (2, verde), (verde, vermelho), (verde, branco), (verde, verde)}
• {1, 2} × {1, 2} = {(1,1), (1,2), (2,1), (2,2)}

Algumas propriedades básicas dos produtos cartesianas:

• A × ∅ = ∅
• A × (B ∪ C) = (A x B) ∪ (A × C)
• | A × B | = | A | x | B |

Aplicações

Teoria dos conjuntos é visto como o fundamento a partir do qual praticamente toda a matemática pode ser derivada. Por exemplo, estruturas em álgebra abstrata , como grupos , campos e anéis, são conjuntos fechados sob uma ou mais operações.

Uma das principais aplicações da teoria dos conjuntos ingênua está construindo relações. Uma relação de um Um domínio de um codomain B é nada, mas um subconjunto de A × B. Tendo em conta este conceito, estamos prontos para ver que o conjunto F de todos os pares ordenados (x, x ^2), onde x é real, é bastante familiar. Tem um conjunto de domínio 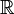e um codomain definido que é igualmente 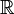, Porque o conjunto de todas as praças é subconjunto do conjunto de todos os reais. Se for colocado em notação funcional, esta relação torna-se f (x) = x ^2. A razão pela qual estes dois são equivalentes é, para qualquer valor dado, y que a função é definida para, a sua correspondente par ordenado, (y, y ²⁾ é um membro do conjunto F.

Teoria dos conjuntos axiomática

Embora inicialmente o teoria dos conjuntos ingênua, que define um conjunto apenas como toda a coleção bem definida, foi bem aceito, ele logo correu em vários obstáculos. Verificou-se que esta definição gerou vários paradoxos, notadamente:

• O paradoxo de Russell - Isso mostra que o "conjunto de todos os conjuntos que não contêm a si mesmos", ou seja, o "set" não existe.
• Paradoxo de Cantor - Isso mostra que "o conjunto de todos os conjuntos" não pode existir.

A razão é que a expressão bem definida não é muito bem definida. Era importante para a teoria dos conjuntos livre desses paradoxos porque quase toda a matemática estava sendo redefinida em termos da teoria dos conjuntos. Em uma tentativa de evitar esses paradoxos, teoria dos conjuntos foi axiomatizada baseado em lógica de primeira ordem , e assim a teoria dos conjuntos axiomática nasceu.

Para a maioria dos fins no entanto, o teoria dos conjuntos ingênua ainda é útil.

Realismo matemático

Penelope Maddy sugeriu que os conjuntos podem ser causalmente eficaz, e de fato compartilhar todas as causal e propriedades espaço-temporais de seus elementos. Assim, quando vejo os três copos sobre a mesa na frente de mim, eu também ver o conjunto também. Ela usou trabalhos recentes na ciência cognitiva e psicologia para apoiar esta posição, salientando que, assim como a uma certa idade, começamos a ver objetos em vez de meras percepções sensoriais, há também uma certa idade em que nós começamos a ver jogos ao invés de apenas objectos.