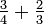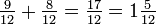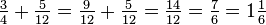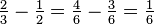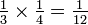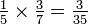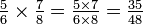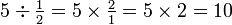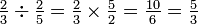Fraction (matemática)

Assuntos Relacionados: Matemática

Sobre este escolas selecção Wikipedia

Crianças SOS, que corre cerca de 200 sos escolas no mundo em desenvolvimento, organizado esta selecção. Crianças SOS tem cuidado de crianças na África por 40 anos. Você pode ajudar o seu trabalho na África ?

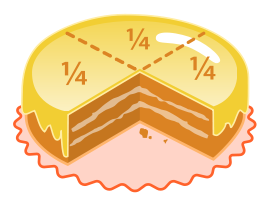
Um bolo com quarto removido. Os restantes três quartos são mostradas.

Em matemática , uma fração (do latim fractus, quebrado) é um conceito de um proporcional relação entre uma parte objeto eo objeto inteiro. Cada fracção é constituída por um denominador (parte inferior) e um numerador (topo), representando (respectivamente) o número de partes iguais de que um objecto é dividido em, e o número dessas partes indicadas para a fracção particular.

Para exemplo, a fracção de ¾ poderia ser usado para representar três partes iguais de um objecto de todo, se fosse dividido em quatro partes iguais. Porque é impossível dividir algo em partes iguais de zero, zero, nunca pode ser o denominador de uma fração (ver divisão por zero). Uma fracção com igual numerador e denominador é igual a um (por exemplo, 5/5 = 1) e a forma de fracção é raramente, se alguma vez, dada como um resultado final.

A fracção é um exemplo de um tipo específico de rácio, em que os dois números estão relacionados de uma relação de parte para o todo, em vez de como uma relação comparativa entre duas quantidades separadas. A fracção é um quociente de números , a quantidade obtida quando o numerador é dividido pelo denominador. Assim ¾ representa três dividido por quatro, em decimais 0,75, como uma percentagem de 75%. As três partes iguais do bolo é 75% de todo o bolo.

Em matemática superior, uma fração é visto como um elemento de um campo de fracções.

Historicamente, qualquer número que não representam um todo foi chamado de "fração". Os números que nós hoje chamamos de "decimais" foram originalmente chamado de "frações decimais"; os números que hoje chamamos de "frações" foram chamados de "frações vulgares", a palavra "vulgar", que significa "lugar comum".

O numerador e denominador de uma fracção podem ser separados por uma linha inclinada chamado solidus ou cortar, por exemplo ¾, ou pode ser escrito acima e abaixo de uma linha horizontal chamado vinculum, assim: $\ Tfrac {3} {4}$ .

A solidificao pode ser omitida do estilo oblíqua (por exemplo, ^{3 e} _4), onde o espaço é curto e o sentido é óbvio a partir do contexto, por exemplo, em sinais de trânsito em alguns países.

As fracções são usados com mais freqüência quando o denominador é relativamente pequeno. É mais fácil para multiplicar 32 por 3/16 do que fazer o mesmo cálculo usando equivalente decimal da fração (0,1875). É também mais preciso multiplicar por 15 ⅓, por exemplo, do que está a multiplicar por 15 uma aproximação decimal de um terço. Para alterar uma fracção para um número decimal, divida o numerador pelo denominador, e arredondar para a precisão desejada.

As fracções são também números racionais, em que significa que o denominador e numerador são números inteiros.

O termo é também usado nas expressões relacionadas, tal como fracção contínua e fração algébrica-ver casos especiais abaixo.

Formas de fracções

Vulgar, apropriado, e fracções impróprias

Uma fracção vulgar (ou fracção comum) é um número racional escrito como um número inteiro (o numerador) dividido por um número inteiro não zero (o denominador), por exemplo, 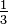$\ Tfrac {1} {3}$ , $\ Tfrac {3} {4}$ e $\ Tfrac {4} {3}$ .

Uma fracção vulgar é dito ser uma fracção adequada, se o valor absoluto do numerador é menor do que o valor absoluto do denominador, isto é, se o valor absoluto da fracção inteira é inferior a 1 (por exemplo, 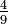$\ Tfrac {4} {9}$ ) -but Uma fracção incorrecto (EUA, britânica ou Australiana) ou superior fracção pesada (British apenas), se o valor absoluto do numerador é maior do que ou igual ao valor absoluto do denominador (p.ex. 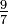$\ Tfrac {9} {7}$ ).

Números mistos

Um número misto é a soma de um número inteiro e uma fracção adequada. Por exemplo, referindo-se em dois bolos inteiros e três quartos de outro bolo, o todo e as partes das frações do número está escrito ao lado do outro: 2 + 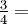$\ Tfrac {3} {4} =$ 2 $\ Tfrac {3} {4}$ .

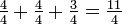Uma fração imprópria pode ser pensado como uma outra maneira de escrever um número misto; no "2 $\ Tfrac {3} {4}$ "Exemplo acima, imaginar que os dois bolos inteiros são cada um dividido em trimestres. Inteiras cada um contribui bolo $\ Tfrac {4} {4}$ ao total, assim $\ Tfrac {4} {4} + \ tfrac {4} {4} + \ tfrac {3} {4} = \ tfrac {11} {4}$ é outra maneira de escrever 2 $\ Tfrac {3} {4}$ .

Um número misto pode ser convertido para uma fracção incorrecto em três passos:

Multiplique toda a parte pelo denominador da parte fracionária.
Adicionar o numerador da parte fracionária para esse produto.
A soma resultante é o numerador da nova fracção (indevida), e a nova denominador é a mesma que a da parte fraccionada do número misto.

Da mesma forma, uma fracção incorrecto pode ser convertido a uma série mista:

Divida o numerador pelo denominador.
O quociente (sem restante) torna-se toda a parte eo restante se torna o numerador da parte fracionária.
O novo denominador é a mesma que a da fracção incorrecto originais.

Fracções equivalentes

Multiplicando o numerador e denominador de uma fracção pelo mesmo número de resultados (não-zero) em uma nova fracção que é dito para ser equivalente à fracção inicial. A palavra equivalente significa que as duas fracções ter o mesmo valor. Isto é verdade porque, para qualquer número 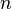$n$ , Multiplicando pela $\ Tfrac {n} {n}$ é realmente multiplicando por um, e qualquer número multiplicado por um tem o mesmo valor que o número original. 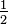Por exemplo, considere a fracção $\ Tfrac {1} {2}$ : Quando o numerador e denominador são ambos multiplicado por dois, o resultado é 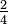$\ Tfrac {2} {4}$ , Que tem o mesmo valor (0,5) como 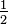$\ Tfrac {1} {2}$ . 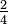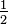Para imaginar isso visualmente, imagine cortar o exemplo bolo em quatro partes; dois dos pedaços juntos ( $\ Tfrac {2} {4}$ ) Representam metade do bolo ( $\ Tfrac {1} {2}$ ).

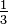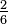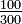Por exemplo: $\ Tfrac {1} {3}$ , $\ Tfrac {2} {6}$ , $\ Tfrac {3} {9}$ e $\ Tfrac {100} {300}$ todas as fracções são equivalentes.

Dividindo o numerador eo denominador de uma fracção pelo mesmo número diferente de zero também irá produzir uma fração equivalente. isto é chamado a redução ou de simplificar a fracção. Uma fração na qual o numerador eo denominador não possuem factores comuns (exceto um) é dito ser irredutível ou em seus termos mais simples ou mais baixas. Por exemplo, $\ Tfrac {3} {9}$ não é menor em termos tanto porque 3 e 9 pode ser exatamente dividido por 3. 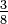Em contraste, $\ Tfrac {3} {8}$ é menor em termos, o único número que é um fator de ambos 3 e 8 é 1.

Recíprocos e o "denominador invisível"

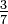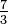O recíproco de uma fração é outra fração com numerador e denominador revertida. O recíproco da $\ Tfrac {3} {7}$ , Por exemplo, é $\ Tfrac {7} {3}$ .

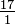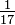Uma vez que qualquer número dividido por um resulta no mesmo número, é possível escrever qualquer número inteiro como uma fracção utilizando um como o denominador: 17 = $\ Tfrac {17} {1}$ (1 é muitas vezes referida como o "denominador invisível"). Portanto, excepto para zero, cada fracção ou um número inteiro tem recíproco. O recíproco de 17 seria $\ Tfrac {1} {17}$ .

Fracções complexas

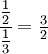Uma fracção complexo (ou fracção do composto) é uma fracção em que o numerador e denominador conter uma fracção. Por exemplo, $\ Cfrac {\ tfrac {1} {2}} {\ tfrac {1} {3}}$ é uma fracção complexo. Para simplificar uma fração complexo, divida o numerador pelo denominador, como com qualquer outra fracção: $\ Cfrac {\ tfrac {1} {2}} {\ tfrac {1} {3}} = \ tfrac {3} {2}$ .

Aritmética com fracções

Frações, como números inteiros, obedecer à comutativa , associativa , e leis distributivas e do Estado contra a divisão por zero.

Comparando frações

Comparando frações com o mesmo denominador requer apenas comparando os numeradores.

$\ Tfrac {3} {4}> \ tfrac {2} {4}$ como $3> 2$ .

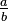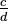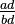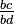A fim de comparar as fracções com denominadores diferentes, estes são convertidos para um denominador comum: comparar $\ Tfrac {a} {b}$ e $\ Tfrac {c} {d}$ , Estes são convertidos em $\ Tfrac {} {ad bd}$ e $\ Tfrac {bc} {bd}$ , Onde bd é o produto dos denominadores, e, em seguida, o anúncio numeradas e bc são comparados.

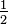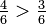
$\ Tfrac {2} {3}$ ? $\ Tfrac {1} {2}$ dá $\ Tfrac {4} {6}> \ tfrac {3} {6}$

Este método é também conhecido como o método de "cross-multiplicar", que pode ser explicada através da multiplicação dos números de topo e de fundo transversalmente. O produto dos denominadores é usado como um comum (mas não é necessário o menos comum) denominador.

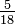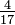
$\ Tfrac {5} {18}$ ? $\ Tfrac {4} {17}$

Multiplique 17 por 5 e 18 por 4. Coloque os produtos das equações em cima dos denominadores. O maior número identifica a maior fracção. Portanto 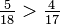$\ Tfrac {5} {18}> \ tfrac {4} {17}$ como 17 x 5 = 85 é maior do que 18 x 4 = 72.

A fim de trabalhar com números menores, o menos denominador comum é usado em vez do produto. As fracções são convertidos em fracções com o denominador comum, e, em seguida, as numeradas são comparados.

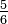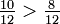
$\ Tfrac {5} {6}$ ? $\ Tfrac {3} {4}$ dá $\ Tfrac {10} {12}> \ tfrac {8} {12}$

Alguns textos de matemática com base em padrões tais como Matemática conectados omitir instrução de denominadores menos comuns inteiramente. Esse texto apresenta a utilização de tiras de "fracção" (uma faixa de papel dobrado em fracções ") ou fracções de referência", tais como um meio contra a qual uma fracção tal como dois quintos podem ser comparados. Embora tais métodos podem ser úteis para construir o entendimento conceitual, eles são controversos como eles não são eficazes para além do ensino fundamental, e tais textos são frequentemente suplementados por professores com o método padrão.

Adição

A primeira regra de adição é que apenas como quantidades pode ser adicionado; por exemplo, várias quantidades de trimestres. Ao contrário de quantidades, como a adição terços para trimestres, deve primeiro ser convertidos para gostar quantidades conforme descrito abaixo:

Adicionando como quantidades

Imagine um bolso contendo dois quartos, e outro bolso contendo três quartos; No total, há cinco trimestres. Uma vez que quatro quadrantes é equivalente a uma (de dólar), este pode ser representado como se segue:

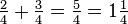$\ Tfrac24 + \ tfrac34 = \ tfrac54 = 1 \ tfrac14$ .

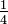Se $\ Tfrac12$ de um bolo é para ser adicionado ao $\ Tfrac14$ de um bolo, as peças precisam ser convertidas em quantidades comparáveis, como bolo oitavos ou bolo quartos.

Adicionando ao contrário de quantidades

Para adicionar fracções contendo quantidades (por exemplo, ao contrário de trimestres e terços), é necessário para converter todos os montantes a gostar quantidades. É fácil trabalhar com o tipo de fração para converter; basta multiplicar juntos os dois denominadores (número inferior) de cada fração.

Para a adição a trimestres terços, ambos os tipos de fracção são convertidos em $\ Tfrac14 \ times \ tfrac13 = \ {12} tfrac1$ (duodécimos).

Considere a adição de duas quantidades seguintes:

$\ Tfrac34 + \ tfrac23$

Em primeiro lugar, converter 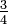$\ Tfrac34$ em duodécimos, multiplicando o numerador eo denominador por três: 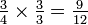$\ Tfrac34 \ times \ tfrac33 = \ {12} tfrac9$ . Note que 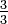$\ Tfrac33$ é equivalente a 1, o que mostra que 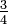$\ Tfrac34$ é equivalente ao resultante $\ Tfrac9 {12}$

Em segundo lugar, converter 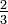$\ Tfrac23$ em duodécimos, multiplicando o numerador eo denominador por quatro: 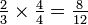$\ Tfrac23 \ times \ tfrac44 = \ {12} tfrac8$ . Note que 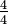$\ Tfrac44$ é equivalente a 1, o que mostra que 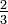$\ Tfrac23$ é equivalente ao resultante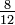 $\ Tfrac8 {12}$

Agora, pode ser visto que:

$\ Tfrac34 + \ tfrac23$

é equivalente a:

$\ Tfrac9 {12} + \ tfrac8 {12} = \ tfrac {17} {12} = 1 \ tfrac5 {12}$

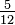Este método sempre funciona, mas às vezes há um denominador menor que pode ser usado (um denominador menos comum). Por exemplo, para adicionar $\ Tfrac {3} {4}$ e $\ Tfrac {5} {12}$ o denominador 48 pode ser utilizada (o produto de 4 e 12), mas o denominador menor 12 também pode ser usado, sendo o mínimo múltiplo comum de 4 e 12.

$\ Tfrac34 + \ tfrac {5} {12} = \ tfrac {9} {12} + \ tfrac {5} {12} = \ tfrac {14} {12} = \ tfrac76 = 1 \ tfrac16$

Subtração

O processo para subtrair fracções é, na sua essência, o mesmo que o de adicioná-los: encontrar um denominador comum, e cada fracção para alterar uma fracção equivalente com o denominador comum escolhida. A fracção resultante terá que denominador e numerador será o resultado da subtracção dos numeradas das fracções originais. Por exemplo,

$\ Tfrac23- \ tfrac12 = \ tfrac46- \ tfrac36 = \ tfrac16$

Multiplicação

Ao multiplicar ou dividir, pode ser possível escolher para cancelar para baixo transversalmente múltiplos que compartilham um fator comum. Por exemplo:

1/ 2 X 1 1/ 7 1 = 1/1 X 1/1. A seguir irá explicar como concluir essa equação.

A multiplicação por números inteiros

Considerando o exemplo acima bolo, se você tiver um quarto do bolo e você multiplicar o montante por três, então você acaba com três quartos. Podemos escrever este numericamente como segue:

$\ textstyle {3 \ times {1} \ over 4 = {3 \ mais de 4}} \, \!$

Como outro exemplo, suponha que cinco pessoas trabalham durante três horas fora de um dia de sete horas (isto é. Para 3/7 da jornada de trabalho). No total, eles vão ter trabalhado durante 15 horas (5 x 3 horas cada), ou 15/7 de um dia. Desde 7/7 de um dia é um dia inteiro e 14/7 é de dois dias, em seguida, no total, eles vão ter trabalhado para 2 dias e um sétimo de um dia. Numericamente:

$\ textstyle {5 \ times {3} \ over 7 = {15} \ over 7 = 2 {1 \ over 7}} \, \!$

A multiplicação por frações

Considerando o exemplo acima bolo, se você tiver um quarto do bolo e você multiplicar o valor por um terceiro, então você acaba com um duodécimo do bolo. Em outras palavras, um terço de um quarto (ou uma terceira vezes quarto) é um XII. Por quê? Porque nós estamos dividindo cada trimestre em três pedaços, e quatro trimestres vezes três faz 12 peças (ou duodécimos). Podemos escrever este numericamente como segue:

$\ textstyle {{1 \} \ mais de 3 vezes {1} \ over 4 = {1 \ over 12}} \, \!$

Como outro exemplo, suponha que cinco pessoas fazem um trabalho de valor igual, que totaliza três horas fora de um dia de sete horas. Cada pessoa terá feito um quinto do trabalho, então eles vão ter trabalhado por um quinto do 3/7 de um dia. Numericamente:

$\ textstyle {{1 \} \ mais de 5 vezes {3} \ over 7 = {3 \ mais de 35}} \, \!$

Regra geral

Você deve ter notado que quando nós multiplicamos frações, multiplicamos os dois numeradores (os melhores números) para fazer o novo numerador, e multiplicar os dois denominadores (os números em baixo) para fazer o novo denominador. Por exemplo:

$\ textstyle {{5 \ mais de 6} {7 \ times \ mais de 8} = {5 \ times 7 \ mais de 6 \ times 8} = {35 \ over 48}} \, \!$

A multiplicação por números mistos

Ao multiplicar números mistos, é melhor para converter toda a parte do número misto em uma fração. Por exemplo:

$\ Textstyle {3 \ times 2 {3} \ over 4 = 3 \ times \ left ({{8 \ over 4} {3 + \ over 4}} \ right) = 3 \ times {11} \ over 4 = { 33 \ over 4} = 8 {1 \ over 4}} \, \!$

Em outras palavras, 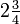$\ Textstyle {2 {3 \ 4}} sobre$ é o mesmo que 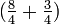$\ Textstyle {({8 \ over 4} {3 + \ over 4})}$ , Fazendo 11 quartos no total (porque dois bolos, cada um dividido em trimestres faz 8/4 total) e 33 quartos é 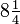$\ Textstyle {8 {1 \ over 4}}$ , Uma vez que oito bolos, cada uma formada por trimestres, é 32 quartos no total.

Divisão

Para dividir por uma fracção, basta multiplicar por o recíproco da fracção.

$\ textstyle {5 \ div {1} \ over 2 = 5 \ vezes {2} \ mais de 1 = 5 \ times 2 = 10}$

$\ Textstyle {{2 \ over 3} \ div {2 \ over 5} = {2 \ over 3} \ times {5} \ over 2 = {10} \ over 6 = {\ 5 ao longo de 3}}$

Para entender por que isso funciona, considere o seguinte:

Pergunta, faz

$\ Textstyle {\ frac ab \ div \ frac cd = \ frac ab \ times \ dc frac}$

Dado / Accepted

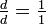I. Qualquer número dividido por si só é um (por exemplo, $\ Textstyle {\ frac d d = \ frac 1 1}$ )

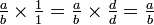II. Quando um número é multiplicado por um que não altere (por exemplo, $\ Textstyle {\ frac ab \ times \ frac 1 1 = \ frac ab \ times \ frac dd = \ frac ab}$ )

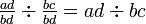III. Se duas fracções tem denominadores comuns, então as numeradas, pode ser dividido para encontrar o quociente (p.ex. $\ Textstyle {\ frac {} {ad bd} \ div \ frac {bc} {} = bd ad \ div bc}$ )

Prova

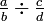1. $\ Textstyle {\ frac {a} {b} \ div \ frac {c} {d}}$ , Problem

2. 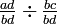$\ Textstyle {\ frac {} {ad bd} \ div \ frac {bc} {bd}}$ , Multiplicado pela primeira fracção por 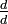$\ Textstyle {\ frac d d}$ e a segunda fracção por 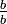$\ Textstyle {\ frac b b}$ , Que é a mesma como a multiplicação por um, e como acima aceites (I e II) não altera o valor da fracção

Nota: Estes valores de uma foram escolhidas para que as fracções que têm um denominador comum; bd é o denominador comum.

3. 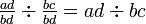$\ Textstyle {\ frac {} {ad bd} \ div \ frac {bc} {} = bd ad \ div bc}$ , A partir do que foi dado em (III)

4. 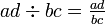$\ Textstyle {ad \ div bc = \ frac {} {bc ad}}$ , Notação Changed

5. $\ Textstyle {\ frac {} {bc ad} = \ frac ab \ times \ frac dc}$ , Pode ser visto

6. $\ Textstyle {\ frac um b \ times \ frac d c}$ , Solução

Cerca de 4.000 anos atrás egípcios dividido com frações que usam métodos ligeiramente diferentes, utilizando múltiplos menos comuns com frações de unidade.

Convertendo decimais para frações de repetição

Os números decimais, enquanto que sem dúvida mais útil para trabalhar com ao realizar cálculos, não têm o mesmo tipo de precisão que frações regulares (como são explicadas neste artigo) tem. Às vezes, um número infinito de casas decimais é necessário para transmitir o mesmo tipo de precisão. Assim, muitas vezes é útil para converter números decimais em frações de repetição.

Para padrões de repetição mais, um simples divisão do padrão pelo mesmo número de noves como números tem será suficiente. Por exemplo (o padrão é destacada em negrito):

0. 5 ... 55 = 5/9

0. 264 264,264 ... = 264/999

0. 6.291 62.916.291 ... = 6291/9999

Em caso zeros preceder o teste padrão, os noves são sufixo o mesmo número de zeros:

0,0 5 ... 55 = 5/90

0,000 392 392392 ... = 392/999000

0.00 12 1212 ... = 12/9900

No caso de um conjunto não-repetição de decimais preceder o padrão (como 0,1523 987 987987 ...), temos de igualá-la como a soma das partes não-repetindo e repetindo:

0,1523 + ,0000987987987 ...

Em seguida, converter ambos para frações. Uma vez que a primeira parte é não repetição, que não é convertido de acordo com o modelo dado acima:

1523/10000 + 987/9990000

Nós adicionamos estas frações, expressando ambos com um divisor comum ...

1521477/9990000 + 987/9990000

E adicioná-los.

1522464/9990000

Finalmente, simplificá-lo:

31718/208125

Casos especiais

Uma fracção é uma fracção de unidade vulgar com um numerador de 1, por exemplo, 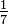$\ Tfrac {1} {7}$ .

Um Fracção egípcio é a soma das fracções unitárias distintas, por exemplo, $\ Tfrac {1} {2} + \ tfrac {1} {3}$ .

A fração dyadic é uma fração vulgar em que o denominador é um potência de dois, por exemplo, 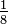$\ Tfrac {1} {8}$ .

Uma expressão que tem a forma de uma fração, mas na verdade representa a divisão por ou em um número irracional é às vezes chamado de "fração irracional". Um exemplo comum é $\ Textstyle {\ frac {\ pi} {2}}$ , A medida em radianos de um ângulo reto.

Números racionais são o campo quociente de inteiros. Funções racionais são funções avaliadas na forma de uma fração, onde o numerador eo denominador são polinômios. Estas expressões racionais são o campo quociente dos polinômios (mais de alguns domínio integral).

A fração continuada é uma expressão como $a_0 + \ frac {1} {a_1 + \ frac {1} {a_2 + ...}}$ , Em que o um _i são números inteiros. Este não é um elemento de um campo quociente.

O termo fração parcial é utilizado em álgebra, quando em decomposição expressões racionais (uma fração com uma expressão algébrica no denominador). O objetivo é escrever a expressão racional como a soma de outras expressões racionais com denominadores de menor grau. Por exemplo, a expressão racional 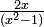$\ Textstyle {2x \ over (x ^ 2-1)}$ pode ser reescrita como a soma de duas fracções: 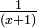$\ Textstyle {1 \ over (x + 1)}$ e $\ Textstyle {1 \ over (x-1)}$ .

Ferramentas pedagógicas

Em escolas primárias, as fracções foram demonstradas através de Hastes Cuisenaire.

Os pais de crianças frações de aprendizagem também deve estar ciente que a aritmética é frequentemente ensinada de forma muito diferente com matemática de reforma. Muitos textos não dão instrução dos métodos convencionais que podem utilizar o mínimo denominador comum, para comparar adicionar ou frações. Alguns introduzem recém-desenvolvido conceitos como "tiras" de fração e frações de benchmark (1/2, 1/4, 3/4 e 10/1) que não estão familiarizados com os pais ou matemáticos. Alguns estão preocupados que esses métodos não irá preparar os alunos para a matemática na faculdade ou escola. Se este for o caso, os pais podem pedir suas escolas para complementar a aprendizagem de seus filhos com métodos padrão ou mudar para textos que dão instrução em métodos tradicionais. Aritmética fração é normalmente ensinado e dominou desde o final de elementar a médio ou a escola secundária. No entanto, alguns textos, como a Matemática Conectados não discutem divisão de frações em tudo, mesmo através de 8ª série em CMP

Veja também os links externos abaixo.

História

O primeiro uso conhecido de frações decimais é ca. 2800 aC como antiga do Vale do Indo unidades de medida . O Egípcios usavam frações egípcio ca. 1000 aC. Os gregos usadas frações de unidade e mais tarde continuou frações e seguidores do filósofo grego Pitágoras , ca. 530 aC, descobriu que o raiz quadrada de dois não pode ser expressa como uma fracção. Em 150 aC Matemáticos Jain em India escreveu o "Sthananga Sutra", que contém os trabalhos sobre a teoria dos números, operações aritméticas, operações com frações .

Retirado de " http://en.wikipedia.org/w/index.php?title=Fraction_(mathematics)&oldid=198200701 "

Home Page - YouTube Channel