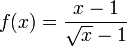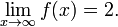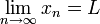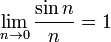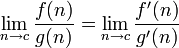Limite (matemática)

O Wikibook Cálculo tem uma página sobre o tema de: Limites

Em matemática , o conceito de uma "limite" é usado para descrever o comportamento de uma função como seu argumento ou "se aproxima" a algum ponto, ou como ele se torna arbitrariamente grande; ou o comportamento de uma sequência elementos 's como sua índice aumenta indefinidamente. Os limites são usados no cálculo e outros ramos da análise matemática para definir derivados e continuidade.

O conceito do "limite de uma função" é ainda mais generalizada ao conceito de rede topológica, enquanto que o limite de uma sequência é intimamente relacionada com limite e limite em directo teoria da categoria.

Limite de uma função

Suponha f (x) é uma função real e c é um número real . A expressão:

significa que f (x) pode ser feito para ser o mais próximo possível G conforme desejado, fazendo x suficientemente perto para c. Nesse caso, dizemos que "o limite do ƒ de x, quando x tende c, é L". Note-se que esta declaração pode ser verdadeiro mesmo se 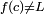. Na verdade, a função f (x) precisa nem mesmo ser definida no c. Dois exemplos ajudam a ilustrar isso.

Considerar quando x tende a 2. Neste caso, F (x) é definido entre 2 e igual ao seu limite de 0,4:

F (1,9)	F (1,99)	F (1,999)	f (2)	F (2,001)	F (2,01)	F (2,1)
0,4121	0,4012	0,4001	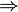0,4	0,3998	0,3988	0,3882

Quando x tende a 2, ƒ (x) se aproxima de 0,4 e, portanto, temos 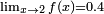. No caso onde , Ƒ é dito ser contínua em x = c. Mas nem sempre é o caso. Considerar

O limite de g (x) quando x tende 2 é de 0,4 (tal como na f (x)), mas 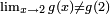; G não é contínua em x = 2.

Ou, considerar o caso em que f (x) é indeterminado em x = c.

Neste caso, à medida que x se aproxima de 1, f (x) é indeterminado em x = 1, mas o limite é igual a 2:

F (0,9)	F (0,99)	F (0,999)	F (1,0)	F (1,001)	F (1,01)	F (1,1)
1.95	1.99	1.999	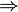undef	2.001	2.010	2.10

Assim, f (x) pode ser feita arbitrariamente próximo do limite de 2 apenas fazendo x suficientemente próximo o suficiente para 1.

Definição formal

Karl Weierstrass definido formalmente um limite da seguinte forma:

Seja f uma função definida em um intervalo aberto contendo c (exceto possivelmente em c) e deixe G ser um número real .

significa que

para cada real ε> 0 existe um verdadeiro δ> 0 tal que para todo x com 0 <| x - c | <δ, temos | f (x) - L | <ε.

A definição formal de um limite é chamado às vezes a forma de delta-epsilon porque ele usa as letras gregas delta (δ) e epsilon (ε). O uso das letras gregas particulares δ e ε é meramente tradicional; a definição iria, é claro, ser inalterado se foram usadas diferentes letras ou símbolos.

Cuidado: Deve notar-se que esta definição fornece um modo para reconhecer um limite sem fornecer um modo para o seu cálculo. Um frequentemente precisa de encontrar um limite usando métodos informais, especialmente quando f (x) é descontínua em c, por exemplo, quando f é um rácio com um denominador que se torna 0 a c. Deve-se verificar que o resultado realmente se enquadra na definição Weierstrass em tais casos.

Limite de uma função no infinito

Um conceito relacionado a limites quando x tende a algum número finito é o limite quando x tende positivo ou negativo infinito . Isso não significa literalmente que a diferença entre x e infinito se torna pequeno, já que o infinito não é um número real; pelo contrário, significa que x ou cresce sem vinculado positivamente (infinito positivo) ou cresce sem ligado de forma negativa (menos infinito).

Por exemplo, considere f (x) = x 2 / (x + 1).

• F (100) = 1,9802
• F (1,000) = 1,9980
• F (10,000) = 1,9998

Como X torna-se muito grande, o valor de f (x) abordagens de 2, e o valor de f (x) pode ser feita como próximo de 2 como se pode desejar apenas escolhendo x suficientemente grande. Neste caso, dizemos que o limite de f (x) quando x tende a infinito é 2. Na notação matemática,

Formalmente, temos a definição

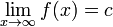Se, e apenas se, para cada ε> 0 existe um n tal que

Note-se que a N na definição geralmente dependerá ε. Uma definição semelhante aplica-se a

Se se considera o domínio de f ser a A linha número real estendida, em seguida, o limite de uma função no infinito pode ser considerado como um caso especial de limite de uma função em um ponto.

Limite de uma seqüência

Considere a seguinte seqüência: 1,79, 1,799, 1,7999, ... Pudemos observar que os números estão "se aproximando" 1.8, o limite da seqüência.

Formalmente, suponha que x _1, x _2, ... é uma seqüência de números reais . Dizemos que o número real L é o limite dessa sequência e escrevemos

Se e apenas se, para cada número real ε> 0 existe um número natural n ₀ (o que dependerá ε) de tal modo que para todo n> n ₀ temos | x _n - L | <ε.

Intuitivamente, isso significa que, eventualmente, todos os elementos da seqüência chegar tão perto quanto nós queremos o limite, uma vez que o valor absoluto | x _n - L | é a distância entre x _n e L. Não cada seqüência tem um limite; se isso acontecer, podemos chamá-lo convergente, divergente em contrário. Pode-se mostrar que uma sequência convergente tem apenas um limite.

O limite de uma seqüência e o limite de uma função estão intimamente relacionados. Por um lado, o limite de uma seqüência é simplesmente o limite no infinito de uma função definida em números naturais . Por outro lado, um limite de uma função f em x, se existir, é o mesmo que o limite da sequência _N x = f (x + 1 / n).

Identidades úteis

• , Em que S é um multiplicador escalar.
• , Em que b é uma constante.

As regras a seguir são válidos apenas se os limites no lado direito existe e são finitos.

• 
• 
• 
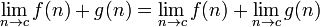
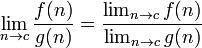• , Se o denominador contendo o limite não é igual a zero,

Se algum dos limites em lado direito é indefinido ou infinito, as regras não necessariamente funciona.

Por exemplo, 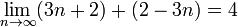mas é indefinido.

Limites de interesse extra

a regra de L'Hôpital

Esta regra usa derivados e tem uma utilização condicionada. Ela apenas pode ser utilizada em formas indeterminadas.

Por exemplo: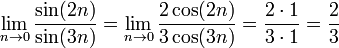

Somatórios

Um curto caminho para escrever o limit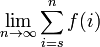e é

Net topológica

Todas as noções acima do limite pode ser unificada e generalizado para arbitrária espaços topológicos, introduzindo topológica redes e definir seus limites. O artigo sobre redes elabora sobre isso.

Uma alternativa é o conceito de limite de filtros em espaços topológicos.

Limite em teoria categoria