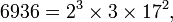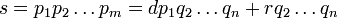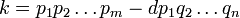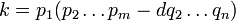Teorema fundamental da aritmética

Em teoria dos números , o teorema fundamental da aritmética (ou único-prime-fatoração teorema) afirma que cada número natural maior que 1 pode ser escrita como um produto único de números primos . Por exemplo,

Não há outros possíveis fatorações de 6936 ou 1200 em números primos. A representação acima colapsos repetiu fatores primos em poderes para facilitar a identificação. Porque a multiplicação é comutativa e associativa , a ordem dos fatores é irrelevante e geralmente escrito da menos para a maior.

Muitos autores tomar os números naturais para começar com 0, que não tem fatoração em primos. Assim, o Teorema 1 de Hardy & Wright (1979) toma a forma: "Todo inteiro positivo, exceto um, é um produto de números primos", e Teorema 2 (sua "Fundamental") afirma singularidade. O número 1 não é primo em si, mas uma vez que é o produto de nenhum número, muitas vezes é conveniente para incluí-lo no teorema pelo regra do produto vazio. (Ver, por exemplo, calculando a gcd ).

Hardy & Wright definir um número anormal de ser um número hipotético que não tem um primeiro-factorização única. Eles provar o teorema fundamental da aritmética, provando que não existe um número anormal.

Aplicações

O teorema fundamental da aritmética estabelece a importância dos números primos. Os números primos são os blocos de construção básicos de qualquer inteiro positivo, no sentido de que cada inteiro positivo pode ser construído a partir do produto de números primos com uma construção única. Encontrar a fatoração em primos de um inteiro permite derivação de todos os seus divisores, tanto de primeira linha e não-prime.

Por exemplo, o factorization acima de 6936 mostra que qualquer divisor positivo de 6936 deve ter o formulário 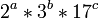, Onde toma um dos quatro valores em {0, 1, 2, 3}, onde leva um dos valores de dois em {0, 1}, e onde toma um dos três valores em {0, 1, 2}. Multiplicando o número de opções independentes em conjunto produz um total de divisores positivos.

Uma vez que os fatorações primos de dois números são conhecidos, o seu maior divisor comum e mínimo múltiplo comum pode ser encontrado rapidamente. Por exemplo, a partir do acima, é mostrado que o maior divisor comum de 6936 e 1200 é 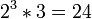. No entanto, se os prime factorizations não são conhecidos, à utilização do Euclidiana algoritmo geralmente requer muito menos do que o cálculo de factoring os dois números.

O teorema fundamental garante que e aditivo multiplicativo funções aritméticas são completamente determinadas por seus valores sobre os poderes de números primos.

Prova

O teorema foi praticamente provado por Euclides , mas a primeira prova completa e correta é encontrada no Disquisitiones Arithmeticae por Carl Friedrich Gauss . Pode ser importante notar que egípcios gosto Ahmes usado anteriormente aspectos práticos da factoring, e menor múltiplo comum, do teorema fundamental da aritmética permitindo uma longa tradição de desenvolver, tal como formalizado por Euclides, e rigorosamente comprovada por Gauss.

Embora à primeira vista o teorema parece "óbvio", ele não se sustenta em sistemas numéricos mais gerais, incluindo muitos anéis de inteiros algébricos. Este foi apontada pela primeira vez por Ernst Kummer, em 1843, em sua obra sobre o último teorema de Fermat . O reconhecimento desse fracasso é um dos primeiros desenvolvimentos em teoria dos números algébricos.

A prova de Euclid

A prova consiste em dois passos. Na primeira etapa, cada número é mostrado como um produto de zero ou mais primos. Na segunda, a prova demonstra que quaisquer duas representações podem ser unificadas numa única representação.

Números compostos não-prime

Suponhamos que havia um número inteiro positivo, que não pode ser escrito como um produto de números primos. Então deve haver um menor número tal (ver bem-ordem): deixá-lo ser n. Este número não pode n ser 1, devido à convenção vazio-produto acima. Não pode ser um número primo, quer, uma vez que qualquer número primo é um produto de um único privilegiada, em si. Assim deve ser um número composto. Assim

n = ab

em que tanto a como b são inteiros positivos menor do que n. Uma vez que n é o número mais baixo que não pode ser escrito como um produto de números primos, tanto a e b pode ser escrito como produtos de números primos. Mas, em seguida,

n = ab

pode ser escrita como um produto de números primos, bem como, uma prova por contradição. Isto é um contra-argumento mínimo.

Prova por descida infinita

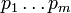A prova da singularidade da fatoração em primos de um dado usos inteiros descida infinita: Assume-se que um determinado número inteiro pode ser escrito como (pelo menos) dois diferentes produtos de números primos: então deve existir um número inteiro menor com tal propriedade. Denotar estas duas factorizações de como e 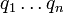, De tal modo que .

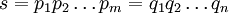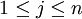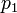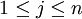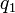Não (Com ) Pode ser igual a qualquer (Com ), Já que há outra forma seria um número inteiro menor factorizar de duas maneiras (removendo fatores primos comuns em ambos os produtos), violando a hipótese acima. Agora, pode-se supor sem perda de generalidade que é um fator primordial menor do que qualquer (Com ). Deixar ser a e quociente o resto da divisão por 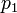. Pelo algoritmo de divisão e são garantidos para ser inteiros tais que e 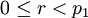. Note que não pode ser 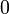, Como que faria 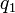um múltiplo de 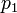e não prime. Também , Desde 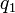é melhor que .

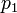Substituindo por 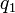na definição original de acima,

Por distributividade:

Definir um novo inteiro 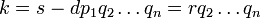. Desde , É claro que deve ser menor do que . E desde 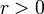, deve ser positiva. A partir da definição de , Segue-se que:

e por factoring fora :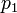

Portanto, existe uma fatoração em primos de que inclui 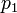. Mas também é verdade que

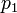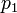Desde , não pode ser um fator primordial de . Assim, por combinação dos factores principais de com , Também é possível construir um factorization privilegiada de que não inclui . Portanto tem dois fatorações principais diferentes, contradizendo a suposição original que é o menor factorizar inteiro em mais de uma maneira. Assim, a suposição inicial deve ser falsa.