
Número binário
Informações de fundo
Crianças SOS feita esta seleção Wikipedia ao lado de outros recursos escolas . Clique aqui para mais informações sobre Crianças SOS.
| Sistemas numerais por cultura |
|---|
|
| Sistemas de posicionamento por base |
| Decimal (10) |
| Ternário equilibrada |
| Lista de sistemas numerais |
O sistema binário, ou base 2 sistema numérico, é um sistema de numeração que representa os valores numéricos usando dois símbolos, geralmente 0 e 1 . Mais especificamente, o habitual base- 2 é um sistema notação posicional com um raiz de 2. Devido à sua implementação direta em circuito eletrônico, o sistema binário é usado internamente por todos os modernos computadores .
História
O antigo escritor indiano Pingala desenvolvido conceitos matemáticos avançados para descrever prosódia, e ao fazer isso apresentou a primeira descrição conhecida de um sistema binário, possivelmente já no século 8 aC. Outros colocá-lo muito mais tarde; R. Hall, Matemática da Poesia, tem "c. 200 aC". O sistema de numeração baseou-se na Olho de Horus sistema de numeração Reino Antigo.
Um conjunto completo de 8 trigramas e 64 hexagramas, análogas às 3 bits e 6-bit números binários, eram conhecidos dos antigos chineses no texto clássico I Ching . Conjuntos semelhantes de combinações binárias têm também sido utilizados em sistemas de adivinhação africanos tradicionais, tais como Ifá, bem como em medievais Ocidental geomancia.
Um arranjo binário ordenada dos hexagramas do I Ching, representando a seqüência decimal de 0 a 63, e um método para gerar o mesmo, foi desenvolvido pelo estudioso chinês e um filósofo Shao Yong no século 11. No entanto, não há nenhuma evidência de que Shao compreendido cálculo binário.
Em 1605 Francis Bacon discutido um sistema pelo qual as letras do alfabeto poderia ser reduzido para sequências de dígitos binários, o que poderia, então, ser codificados como variações pouco visíveis na fonte em qualquer texto aleatório. Importante para a teoria geral da codificação binária, ele acrescentou que esse método pode ser usado com qualquer objeto em todos os: "desde que esses objetos ser capaz de apenas uma diferença dupla, como por Bells, por Trombetas, por Luzes e Tochas, pelo relatório de mosquetes, e os instrumentos da mesma natureza ". (Ver Cifra de Bacon.)
O sistema numérico binário novo foi completamente documentado por Gottfried Leibniz no século 17, em seu artigo Explication de l'Arithmétique Binaire . Sistema de Leibniz usado 0 e 1, como o sistema numérico binário moderna.
Em 1854, britânico matemático George Boole publicou um artigo detalhando marco de um sistema algébrico de lógica que se tornaria conhecido como Álgebra booleana. Seu cálculo lógico era tornar-se instrumental no projeto de circuitos eletrônicos digitais.
Em 1937, Claude Shannon produziu sua tese de mestrado em MIT que implementou Álgebra booleana e aritmética binária utilizando relés eletrônicos e interruptores, pela primeira vez na história. Intitulado Uma análise simbólica de Relay e comutação de circuitos, a tese de Shannon essencialmente fundada prático projeto de circuito digital.
Em novembro de 1937, George Stibitz, em seguida, trabalhar em Bell Labs, completou um computador baseado no revezamento ele apelidado de "Modelo K" (para "itchen K", onde tinha montado ele), que calculado usando adição binária. Bell Labs, assim, autorizou um programa de pesquisa completo no final de 1938 com Stibitz no leme. Seu Complexo Computador Número, completado 8 de janeiro de 1940 , foi capaz de calcular números complexos . Numa demonstração ao Conferência da Sociedade Americana de Matemática em Dartmouth College em 11 de setembro de 1940 , Stibitz foi capaz de enviar a calculadora do número complexo comandos remotos através de linhas telefônicas por um teletipo. Foi a primeira máquina de computação já usou remotamente através de uma linha telefônica. Alguns participantes da conferência que testemunharam a demonstração eram John Von Neumann , John Mauchly, e Norbert Wiener, que escreveu sobre isso em suas memórias.
Representação
Um número binário pode ser representado por qualquer sequência de bits (dígitos binários), que por sua vez podem ser representados por qualquer mecanismo capaz de estar em dois estados mutuamente exclusivos. As seguintes sequências de símbolos pode ser interpretado como todas o mesmo valor numérico binário de 667:
1 0 1 0 0 1 1 0 1 1 | - | - - | | - | | xoxooxxoxx ynynnyynyy

O valor numérico representado em cada caso depende do valor atribuído a cada símbolo. Em um computador, os valores numéricos podem ser representados por dois diferentes voltagens; em um magnético disco, magnético pode ser usado polaridades. A "positivo", "sim", ou "em" estado não é necessariamente equivalente ao valor numérico de um; depende da arquitetura em uso.
De acordo com a representação costumeira de numerais usando algarismos arábicos , números binários são comumente escritos com os símbolos 0 e 1. Quando escrito, números binários são frequentemente subscrito, prefixo ou sufixo para indicar a sua base, ou raiz. As notas seguintes são equivalentes:
- 100101 binário (declaração explícita de formato)
- 100101b (um sufixo que indica o formato binário)
- 100101B (um sufixo que indica o formato binário)
- bin 100101 (um prefixo indicando formato binário)
- 100101 2 (um subscrito indicando base 2 (binário) notação)
- % 100101 (um prefixo que indica o formato binário)
- 0b100101 (um prefixo indicando formato binário, comum em linguagens de programação)
Quando falada, números binários são geralmente ler dígito por dígito, a fim de distingui-los dos números decimais. Por exemplo, o número binário 100 é pronunciada um zero zero, em vez de cem, para fazer a sua natureza binária explícita, e para fins de correcção. Uma vez que o binário numeral 100 é igual ao valor decimal quatro, seria confuso, e numericamente incorrecto, para se referir ao numeral como cem.
Contagem no binário
| Binário | Decimal |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
Contar em binário é semelhante à contagem em qualquer outro sistema de numeração. Começando com um único dígito, contagem prossegue através de cada símbolo, em ordem crescente. Contagem decimal utiliza os símbolos de 0 a 9, enquanto binário utiliza apenas os símbolos 0 e 1.
Quando os símbolos para o primeiro dígito estão esgotados, a próxima maior dígito (à esquerda) é incrementado, e contando começa de novo em 0. Em decimal , contando prossegue assim:
- 000, 001, 002, 007 ..., 008, 009, (mais à direita dígito começa de novo, e próximo dígito é incrementado)
- 0 1 0, 011, 012, ...
- ...
- 090, 091, 092, 097 ..., 098, 099, (dois dígitos mais à direita começar de novo, e próximo dígito é incrementado)
- 1 00, 101, 102, ...
Depois de um dígito atinge 9, um incremento redefine a 0, mas também provoca um incremento do próximo dígito à esquerda. No sistema binário, a contagem é o mesmo, excepto que apenas os dois símbolos 0 e 1 são usadas. Assim, depois de um dígito atinge 1 em binário, um incremento redefine a 0, mas também provoca um incremento do próximo dígito à esquerda:
- 000, 001, (mais à direita dígito começa de novo, e próximo dígito é incrementado)
- 0 1 0, 011, (dois dígitos mais à direita começar de novo, e próximo dígito é incrementado)
- 1 00, 101, ...
Aritmética binária
Aritmética em binário é muito parecido com a aritmética em outros sistemas numéricos. A adição, subtracção, multiplicação, divisão e pode ser realizada em números binários.
Adição

A operação aritmética simples em binário é disso . Adicionando dois números binários de um único dígito é relativamente simples:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10 (carry: 1)
Adicionando dois valores "1" produz o valor "10" (falado como "one-zero"), equivalente ao valor decimal 2. Isto é semelhante ao que acontece em decimal quando certos números de um dígito são somados; se o resultado for igual ou superior ao valor da raiz (10), o dígito à esquerda é incrementado:
- 5 + 5 = 10
- 7 + 9 = 16
Isto é conhecido como a realização na maioria dos sistemas de numeração. Quando o resultado de uma adição excede o valor da raiz, o procedimento é o de "levar a um" para a esquerda, adicionando-o para o próximo valor de posição. Levando funciona da mesma maneira em binário:
1 1 1 1 1 (dígitos realizadas)
0 1 1 0 1
+ 1 0 1 1 1
-------------
= 1 0 0 1 0 0
Neste exemplo, dois números são adicionados juntos: 01101 2 (13 decimal) e 10111 2 (23 decimal). A linha superior mostra os bits de transporte utilizados. Começando na coluna mais à direita, 1 + 1 = 2 10. A 1 é transportada para a esquerda, e a 0 é escrito na parte inferior da coluna mais à direita. A segunda coluna da direita é adicionado: 1 + 0 + 1 = 10 2 novamente; o 1 é realizado, e 0 é escrito na parte inferior. A terceira coluna: 1 + 1 + 1 = 11 2 Desta vez, é levada a um 1, e um 1 é escrito na fila inferior.. Procedendo como este dá a resposta final 100100 2 (36 decimal).
Quando os computadores deve adicionar dois números, a regra de que: x ^ y = x + y% 2 para quaisquer dois bits x e y permite cálculo muito rápido, também.
Subtração
Subtração funciona quase da mesma maneira:
- 0-0 = 0
- 0-1 = 1 (com borrow)
- 1-0 = 1
- 1 - 1 = 0
Um número binário pode ser subtraído dos outros, como segue:
* * * * (Colunas favoritos são emprestados a partir)
1 1 0 1 1 1 0
- 1 0 1 1 1
----------------
= 1 0 1 0 1 1 1
Subtraindo um número positivo é equivalente a adicionar um negativo número de igual valor absoluto ; computadores normalmente usam notação de complemento de dois para representar valores negativos. Esta notação elimina a necessidade de uma operação de "substrato" em separado. A subtracção pode ser resumida com a fórmula:
A - B = A + B + 1 não
Para mais detalhes, consulte complemento de dois.
Multiplicação
Multiplicação em binário é semelhante ao seu homólogo decimal. Dois números A e B podem ser multiplicados por produtos parciais: para cada dígito em B, o produto dessa dígitos em A é calculado e escrito em uma nova linha, deslocado para a esquerda de modo que suas linhas dígito mais à direita com o dígito B que foi utilizado. A soma de todos estes produtos parciais dá o resultado final.
Uma vez que existem apenas dois dígitos em binário, existem apenas dois resultados possíveis de cada multiplicação parcial:
- Se o dígito na B é 0, o produto parcial é também 0
- Se o dígito na B é 1, o produto parcial é igual a A
Por exemplo, os números binários de 1011 e 1010 são multiplicados como se segue:
1 0 1 1 (A)
× 1 0 1 0 (B)
---------
0 0 0 0 ← Corresponde a um zero em B
+ 1 0 1 1 ← Corresponde a uma de um B
+ 0 0 0 0
+ 1 0 1 1
---------------
= 1 1 0 1 1 1 0
Os números binários também podem ser multiplicados com bits após uma ponto binário:
1 0 0 1,1 1 (A) (5,625 em decimal)
× 1 1 1 0.0 (B) (6,25 em decimal)
-------------
1 0 1 1 0 1 ← Corresponde a uma de um B
+ 0 0 0 0 0 0 ← Corresponde a um zero em B
+ 0 0 0 0 0 0
+ 1 0 1 1 0 1
+ 1 0 1 1 0 1
-----------------------
= 1 0 0 0 1 1,0 0 0 1 1 (35,15625 em decimal)
Veja também Algoritmo de multiplicação de Booth.
Divisão
Binary divisão é novamente semelhante ao seu homólogo decimal:
__________
0 1 1 | 1 1 0 1 1
Aqui, o divisor é 101 2, 5 ou decimal, enquanto o dividendo é 11011 2, ou 27 decimal. O procedimento é o mesmo que o de decimal divisão longa; aqui, o divisor 101 2 vai para os primeiros três dígitos 110 2 do dividendo uma vez, portanto, um "1" está escrito na linha superior. Este resultado é multiplicado pelo divisor, e subtraído os três primeiros dígitos do dividendo; o dígito seguinte (um "1") é incluído para obter uma nova sequência de três dígitos:
1
__________
0 1 1 | 1 1 0 1 1
- 1 0 1
-----
0 1 1
O procedimento é então repetido, com a nova sequência, continuando até que os dígitos do dividendo tenham sido esgotadas:
1 0 1
__________
0 1 1 | 1 1 0 1 1
- 1 0 1
-----
0 1 1
- 0 0 0
-----
1 1 1
- 1 0 1
-----
1 0
Assim, o quociente de 11,011 2 101 dividido por 2 é 2 101, como mostrado na linha superior, enquanto o restante, mostrado na linha de fundo, é de 10 2. Em decimal, 27 dividido por 5 é 5, com um resto de 2.
Operações bit a bit
Embora não directamente relacionadas com a interpretação numérica de símbolos binários, seqüências de bits podem ser manipulados usando Boolean operadores lógicos. Quando uma cadeia de símbolos binários é manipulada desta forma, é chamado um operação bit a bit; os operadores lógicos E, OU, e XOR pode ser realizada em bits correspondentes em dois números binários fornecidos como entrada. A lógica NÃO operação pode ser realizada em pedaços individuais em um só algarismo binário fornecido como entrada. Por vezes, tais operações podem ser utilizados como atalhos aritméticos, e pode ter outros benefícios computacionais bem. Por exemplo, uma deslocamento aritmético esquerda de um número binário é o equivalente a multiplicação por um (integral positivo,) potência de dois.
Conversão de e para outros sistemas numéricos
Decimal
Para converter de um número inteiro de base 10 para a sua base numeral-2 (binário) equivalente, o número é dividido por dois, e o restante representa a bit menos significativo. O (inteiro) resultado é novamente dividido por dois, o seu restante é o próximo bit mais significativo. Esse processo se repete até que o resultado de uma maior divisão torna-se zero.
Por exemplo, 10 118, em binária, é:
Operação Restante 118 ÷ 2 = 59 0 59 ÷ 2 = 29 1 29 ÷ 2 = 14 1 14 ÷ 2 = 7 0 7 ÷ 2 = 3 1 3 ÷ 2 = 1 1 1 ÷ 2 = 0 1
Lendo a seqüência de restos de baixo para cima dá o numeral binário  .
.
Este método funciona para a conversão de qualquer base, mas há melhores métodos para bases que são potências de dois, como octal e hexadecimal dado abaixo.
Para converter de base-2 para base-10 é o algoritmo reverso. A partir da esquerda, o dobro do resultado e adicionar o dígito seguinte até que não existem mais. Por exemplo, para converter 110010101101 2 em decimal:
Resultado Dígitos restantes 0 110010101101 0 × 2 + 1 = 1 10010101101 1 × 2 + 1 = 3 0010101101 3 × 2 + 0 = 6 010101101 6 x 2 + 0 = 12 10101101 12 × 2 + 1 = 25 0101101 25 × 2 + 0 = 50 101101 50 × 2 + 1 = 101 01101 101 × 2 + 0 = 202 1101 202 × 2 + 1 = 405 101 405 × 2 + 1 = 811 01 811 × 2 + 0 = 1622 1 1622 × 2 + 1 = 3245
O resultado é 3245 10.
Binário: 1 1 0 0 1 0 1 0 1 1 0 1
Decimal: [(2 ^ 11) * 1] + [(2 ^ 10) * 1] + [(2 ^ 9) * 0] + [(2 ^ 8) * 0] + [(2 ^ 7) * 1 ] + [(2 ^ 6) * 0] + [(2 ^ 5) * 1] + [(2 ^ 4) * 0] + [(2 ^ 3) * 1] + [(2 ^ 2) * 1 ] + [(2 ^ 1) * 0] + [(2 ^ 0) * 1] = 3245
As partes fracionárias de um número são convertidos com métodos semelhantes. Eles estão novamente com base na equivalência de deslocamento com duplicar ou reduzir para metade.
Em um número binário fraccionada tal como ,11010110101 2, o primeiro dígito é 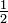 , O segundo
, O segundo  , Etc Então, se existir um 1 na primeira lugar após a casa decimal, em seguida, o número é pelo menos
, Etc Então, se existir um 1 na primeira lugar após a casa decimal, em seguida, o número é pelo menos 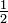 , E vice-versa. Duplo esse número é pelo menos 1. Isso sugere o algoritmo: repetidamente o dobro do número a ser convertido, ficha se o resultado é pelo menos 1, e, em seguida, jogue fora a parte inteira.
, E vice-versa. Duplo esse número é pelo menos 1. Isso sugere o algoritmo: repetidamente o dobro do número a ser convertido, ficha se o resultado é pelo menos 1, e, em seguida, jogue fora a parte inteira.
Por exemplo, 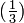 10, em binária, é:
10, em binária, é:
Conversão Resultado 
0. 
0.0 
0,01 
0,010 
0,0101
Assim, a fracção decimal repetindo 0. 3 ... é equivalente à fracção binário de repetição 0. 01 ....
Ou, por exemplo, 0,1 a 10, em binária, é:
Conversão Resultado 0,1 0. 0,1 × 2 = 0,2 <1 0.0 0,2 × 2 = 0,4 <1 0.00 0,4 × 2 = 0,8 <1 0.000 0,8 × 2 = 1,6 ≥ 1 0,0001 0,6 × 2 = 1,2 ≥ 1 0.00011 0,2 × 2 = 0,4 <1 0.000110 0,4 × 2 = 0,8 <1 0.0001100 0,8 × 2 = 1,6 ≥ 1 0.00011001 0,6 × 2 = 1,2 ≥ 1 0,000110011 0,2 × 2 = 0,4 <1 0,0001100110
Esta também é uma fração binária repetição 0,00011 0011 .... Pode vir como uma surpresa que encerra frações decimais pode ter repetindo expansões em binário. É por esta razão que muitos se surpreendem ao descobrir que 0,1 + ... + 0,1, (10 adições) difere de 1 em aritmética de ponto flutuante. De facto, as únicas fracções binárias com expansões de terminação estão na forma de um número inteiro dividido por uma potência de dois, o que não é 1/10.
A conversão final é de binário para decimal frações. A única dificuldade surge com fracções de repetição, mas caso contrário, o método é o de deslocar a fracção de um número inteiro, convertê-lo, como acima, e depois dividir pela potência apropriada de dois na base decimal. Por exemplo:

= 1100 .1011100 11100 ... 
= 1100101110 0,01110 01110 ... 
= 11001 0,01110 01110 ... 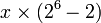
= 1100010101 
= (789/62) 10
Outra forma de conversão de binário para decimal, muitas vezes mais rápido para uma pessoa familiarizada com hexadecimal , é fazê-lo indiretamente-primeira conversão (  em binário) em (
em binário) em (  em hexadecimal) e, em seguida, converter (
em hexadecimal) e, em seguida, converter (  em hexadecimal) em (
em hexadecimal) em (  em decimal).
em decimal).
Para grandes números, estes métodos simples são ineficientes porque eles desempenham um grande número de multiplicações ou divisões onde um operando é muito grande. Um simples algoritmo de divisão e conquista é assintoticamente mais eficaz: dado um número binário, dividimos por 10 k, onde k é escolhido de modo que o quociente é aproximadamente igual ao resto, então cada uma dessas peças é convertido para decimal e os dois são concatenada. Dado um número decimal, que dividi-lo em dois pedaços de aproximadamente o mesmo tamanho, converter cada para binário, em seguida, multiplicar a primeira peça em 10 k e adicioná-los, onde k é o número de dígitos no (mais à direita) peça menos significativo .
Hexadecimal
Binário pode ser convertido para e a partir de hexadecimal um pouco mais facilmente. Isto é devido ao facto de a raiz do sistema de hexadecimal (16) é uma potência da raiz do sistema binário (2). Mais especificamente, 16 = 2 4, por isso leva quatro dígitos do binário para representar um dígito hexadecimal.
A tabela a seguir mostra todos os dígitos hexadecimal, juntamente com o valor decimal equivalente e sequência binário de quatro dígitos:
|
|
|
|
Para converter um número hexadecimal em seu equivalente binário, simplesmente substituir os dígitos binários correspondentes:
- 3A = 16 0011 1010 2
- E7 = 16 1110 0111 2
Para converter um número binário em seu equivalente hexadecimal, dividi-lo em grupos de quatro bits. Se o número de bits não é um múltiplo de quatro, basta inserir extras 0 bits no esquerdo (chamada preenchimento). Por exemplo:
- 01010010 2 = 0101 0010 agrupados com estofamento = 52 16
- 11011101 = 2 1,101 1,101 agrupados DD = 16
Para converter um número hexadecimal em seu equivalente decimal, multiplique o equivalente decimal de cada dígito hexadecimal pelo poder correspondente de 16 e adicionar os valores resultantes:
- C0E7 16 = (12 x 16 3) + (0 × 16 2) + (14 x 16 1) + (7 × 16 0) = (12 × 4096) + (0 × 256) + (14 x 16) + ( 7 x 1) = 49,383 10
Octal
Binário é também facilmente convertido no octal sistema de numeração, uma vez que octal utiliza uma base igual a 8, que é um potência de dois (ou seja, 2 3, por isso leva exatamente três dígitos binários para representar um dígito octal). A correspondência entre octal e números binários é o mesmo que para os oito primeiros dígitos do hexadecimal na tabela acima. Binário 000 é equivalente ao dígito octal 0, 111 é equivalente binário para octal 7, e assim por diante.
Octal Binário 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111
Convertendo de octal para rendimentos binários da mesma forma como faz para hexadecimal :
- 65 8 110 101 2 =
- 17 8 001 111 2 =
E de binário para octal:
- 101100 101 2 = 100 2 = 54 8 agrupados
- 10011 = 2 010 011 2 agrupadas com estofamento = 23 8
E a partir de octal em decimal:
- 65 8 = (6 x 8 1) + (5 × 8 0) = (6 × 8) + (5 × 1) = 53 10
- 127 8 = (1 × 8 2) + (2 x 8 1) + (7 × 8 0) = (1 × 64) + (2 × 8) + (7 x 1) = 87 10
Representando números reais
Não-inteiros pode ser representado usando poderes negativos, que são definidos a partir dos outros dígitos por meio de um ponto da raiz (chamado ponto decimal no sistema decimal). Por exemplo, o número binário 11,01 2 significa assim:
1 2 1 × (1 × 2 = 2) mais 1 x 2 0 (1 × 1 = 1) mais 0 × 2 -1 (0 × ½ = 0) mais 1 × 2 -2 (1 × ¼ = 0,25)
Para um total de 3,25 decimal.
Tudo números racionais diádicos 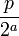 ter uma representação binária do numeral binário encerra tem um número finito de termos após o ponto da raiz. Outros números racionais têm representação binária, mas em vez de terminação, eles se repetem, com uma sequência finita de dígitos repetindo indefinidamente. Por exemplo
ter uma representação binária do numeral binário encerra tem um número finito de termos após o ponto da raiz. Outros números racionais têm representação binária, mas em vez de terminação, eles se repetem, com uma sequência finita de dígitos repetindo indefinidamente. Por exemplo
 =
=  = 0.01010101 ... 01 2
= 0.01010101 ... 01 2
 =
=  = 0.10110100 10110100 10110100 ... 2
= 0.10110100 10110100 10110100 ... 2
O fenómeno de que a representação binária de qualquer racional é ou terminação ou recorrente também ocorre em outros sistemas de numeração à base de radix. Ver, por exemplo, a explicação em decimal . Outra semelhança é a existência de representações alternativas para qualquer representação de terminação, baseando-se no facto de 0.111111 ... é a soma do série geométrica 2 -1 -2 + 2 + 2 + -3 ... que é um.
Números binários que nem terminam nem se repetem representam números irracionais . Por exemplo,
- 0,10100100010000100000100 .... tem um padrão, mas isso não é um padrão recorrente de comprimento fixo, de modo que o número é irracional
- 1,0110101000001001111001100110011111110 ... é a representação binária de
 , A raiz quadrada de 2, outro irracional. Não tem nenhum padrão discernível, embora uma prova de que
, A raiz quadrada de 2, outro irracional. Não tem nenhum padrão discernível, embora uma prova de que  é irracional requer mais do que isso. Ver número irracional .
é irracional requer mais do que isso. Ver número irracional .
