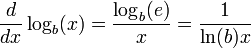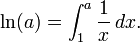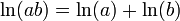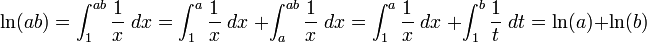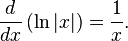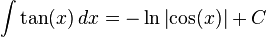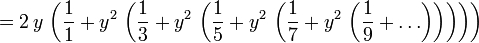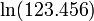Logaritmo natural

Assuntos Relacionados: Matemática

Sobre este escolas selecção Wikipedia

Crianças SOS têm produzido uma seleção de artigos da Wikipédia para escolas desde 2005. Clique aqui para mais informações sobre Crianças SOS.

O logaritmo natural, anteriormente conhecido como o logaritmo hiperbólica, é o logaritmo para o base e, onde e é um irracional constante aproximadamente igual a 2,718 281 828 459. Em termos simples, o logaritmo natural de um número x é a potência à qual e teria de ser aumentada para X igual - por exemplo, o logaritmo natural do próprio e é uma causa de e = ¹ e, enquanto o logaritmo natural de um seria 0, e desde ⁰ = 1. O logaritmo natural pode ser definido para todos os positivos verdadeiros números x como a área sob a curva y = 1 / t de 1 a x, e também pode ser definido para zero não números complexos , como explicado abaixo .

Gráfico da função logaritmo natural. A função rapidamente vai para o infinito negativo quando x tende a 0, mas cresce lentamente até o infinito positivo quando x cresce.

A função logaritmo natural também pode ser definida como a função inversa da função exponencial , que conduz às identidades:

$e ^ {\ ln (x) = x} \ qquad \ mbox {if} x> 0 \, \!$

$\ Ln (e ^ x) = x. \, \!$

Em outras palavras, a função de um logaritmo é bijection partir do conjunto de números reais positivos para o conjunto de todos os números reais. Mais precisamente, é um isomorfismo a partir do grupo de números reais positivos sob a multiplicação para o grupo de números reais sob adição. Representado como uma função :

$\ Ln: \ mathbb {R} ^ + \ a \ mathbb {R}$

Logaritmos pode ser definida para qualquer base positiva diferente de 1, e não só, e são úteis para a resolução de equações em que o desconhecido aparece como o expoente de alguma outra quantidade.

As convenções de notação

Os matemáticos, estatísticos, e alguns engenheiros geralmente entendem ou "log (x)" ou "ln (x)" para significar login _e (x), isto é, o logaritmo natural de x, e escrever "log ₁₀ (x)" se o logaritmo de base 10 destina-se de x.

Alguns engenheiros, biólogos, e alguns outros geralmente escrever "ln (x)" (ou ocasionalmente "log _e (x)") quando querem dizer o logaritmo natural de x, e tomar "log (x)" para significar log ₁₀ (x) ou, no caso de alguns cientistas da computação , log ₂ (X) (lg, embora esta é muitas vezes escrita (x), em vez).

Em mais utilizadas linguagens de programação , incluindo C , C ++ , MATLAB, Fortran, e BASIC , "log" ou "log" refere-se ao logaritmo natural.

Em portáteis calculadoras , o logaritmo natural é denotado ln, enquanto log é o logaritmo de base 10.

Por que ele é chamado de "natural"

Inicialmente, pode parecer que uma vez que o nosso sistema de numeração é base 10 , esta base seria mais "natural" do que base e. Mas matematicamente, o número 10 não é particularmente significativo. Seu uso culturalmente como a base para muitas sociedades 'numeração sistemas provavelmente decorre de seres humanos' número típico de dedos. E outras culturas ter baseado os seus sistemas de contagem sobre essas escolhas como 5, 20, e 60.

Log _e é um log "natural", pois brota automaticamente a partir de, e aparece com tanta frequência, em matemática. Por exemplo, considere o problema de diferenciar uma função logarítmica:

$\ Frac {d} {dx} \ log_b (x) = \ frac {\ log_b (e)} {x} = \ frac {1} {\ ln (b) x}$

Se o base b é igual e, em seguida, o derivado é simplesmente 1 / x, e em x = 1 deste derivado é igual a 1. Um outro sentido em que o logaritmo base- e é o mais natural é que ele pode ser facilmente definida em termos de um simples integrante ou série de Taylor e isso não é verdade de outros logaritmos.

Mais sentidos dessa naturalidade não fazem uso do cálculo. Como exemplo, há um número de série simples envolvendo o logaritmo natural. Na verdade, Pietro e Mengoli Nicholas Mercator chamou Logarithmus naturalis algumas décadas antes de Newton e Leibniz desenvolveram o cálculo.

Definições

Ln (x) definido como a área sob a curva F (x) = 1 / x.

Formalmente, ln (a) pode ser definida como a área sob o gráfico de 1 / x de 1 a A, que é como a integrante ,

$\ Ln (a) = \ int_1 ^ a \ frac {1} {x} \, dx.$

Isso define um logaritmo porque satisfaz a propriedade fundamental de um logaritmo:

$\ Ln (ab) = \ ln (a) + \ ln (b) \, \!$

Isto pode ser demonstrado por deixando $t = \ tfrac xa$ do seguinte modo:

$\ Ln (ab) = \ int_1 ^ {ab} \ frac {1} {x} \; dx = \ int_1 ^ a \ frac {1} {x} \; dx \; + \ Int_a ^ {ab} \ frac {1} {x} \; dx = \ int_1 ^ {a} \ frac {1} {x} \; dx \; + \ Int_1 ^ {b} \ frac {1} {t} \; dt = \ ln (a) + \ ln (b)$

O número e, em seguida, pode ser definido como o número único verdadeiro tal que LN (a) = 1.

Alternativamente, se a função exponencial tem sido definida em primeiro lugar usando um série infinita, o logaritmo natural pode ser definida como a sua função inversa , ou seja, ln (x) que é função tal que $e ^ {\ ln (x) = x} \!$ . Uma vez que a faixa da função exponencial em argumentos reais é todos os números reais positivos e uma vez que a função exponencial é estritamente crescente, isto é bem definido para todos os x positiva.

Derivada, série de Taylor

O derivado do logaritmo natural é dada pela

$\ Frac {d} {dx} \ ln (x) = \ frac {1} {x}. \,$

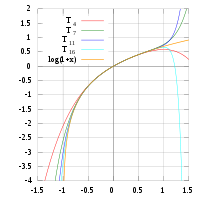
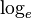Os polinômios de Taylor para $\ Log_e$ (1 + x) só fornecem aproximações precisas na faixa de -1 <x ≤ 1. Note-se que, para x> 1, os polinômios Taylor de grau mais elevado são piores aproximações.

Isto leva à série de Taylor para $\ Ln (1 + x)$ em torno de $0$ ; também conhecido como o Série Mercator

$\ Ln (1 + x) = \ sum_ {n = 1} ^ \ infty \ frac {(- 1) ^ {n + 1}} {n} x ^ n = x - \ frac {x ^ 2} {2 } + \ frac {x ^ 3} {3} - \ cdots \ quad {\ rm para} \ quad \ left | x \ right | \ leq 1 \ quad$

${\ Rm a menos} \ quad x = -1$

À direita é uma imagem de 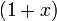$\ Ln$ $(1 + x)$ e alguns de seus polinômios Taylor em torno de $0$ . Estas aproximações convergem para a função apenas na região -1 <x ≤ 1; fora dessa região os de grau superior polinômios Taylor são piores aproximações para a função.

Substituindo x 1 para x, obtemos uma forma alternativa para ln (x) em si, ou seja,

$\ Ln (x) = \ sum_ {n = 1} ^ \ infty \ frac {(- 1) ^ {n + 1}} {n} (x-1) ^ n$

$\ Ln (x) = (x - 1) - \ frac {(x-1) ^ 2} {2} + \ frac {(x-1) ^ 3} {3} - \ frac {(x-1) ^ 4} {4} \ cdots$

${\ Rm para} \ quad \ left | x-1 \ right | \ leq 1 \ quad {\ rm a menos} \ quad x = 0.$

Ao utilizar o Euler transformar na série de Mercator, obtém-se o seguinte, que é válida para qualquer x com valor absoluto superior a 1:

$\ Ln {x \ over {x-1}} = \ sum_ {n = 1} ^ \ infty {1 \ over {nx ^ n}} = {1 \ over x} + {1 \ over {2x ^ 2} } + {1 \ over {3x ^ 3}} + \ cdots$

Esta série é semelhante a um BBP-tipo fórmula.

Observe também que 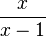$x \ over {x-1}$ é a sua própria função inversa, de modo a produzir o logaritmo natural de um determinado número N, simplesmente colocar em $n \ over {n-1}$ para x.

O logaritmo natural na integração

O logaritmo natural simples permite a integração de funções da forma g (x) = f (x) / f (x): um anti derivada de g (x) é dado por ln (| f (x) |). Este é o caso devido à regra da cadeia e o seguinte fato:

$\ {D \ over dx} \ left (\ ln \ left | x \ right | \ right) = {1 \ over x}.$

Em outras palavras,

$\ Int {1 \ over dx x} = \ ln | x | + C$

$\ Int {\ frac {f '(x)} {f (x)} \, dx} = \ ln | f (x) | + C.$

Aqui é um exemplo no caso de g (x) = tan (x):

$\ Int \ tan (x) \, dx = \ int {\ sin (x) \ over \ cos (x)} \, dx$

$\ Int \ tan (x) \, dx = \ int {- {d \ over dx} \ cos (x) \ over {\ cos (x)}} \, dx.$

Deixando f (x) = cos (x) e f (x) = - sen (x):

$\ Int \ tan (x) \, dx = - \ ln {\ left | \ cos (x) \ right |} + C$

$\ Int \ tan (x) \, dx = \ ln {\ left | \ sec (x) \ right |} + C$

onde C é uma constante arbitrária de integração.

O logaritmo natural pode ser integrado usando integração por partes:

$\ Int \ ln (x) \, dx = x \ ln (x) - x + C.$

Valor numérico

Para calcular o valor numérico do logaritmo natural de um número, a expansão em série de Taylor pode ser reescrita como:

$\ ln (1 + x) = x \, \ left (\ frac {1} {1} - x \, \ left (\ frac {1} {2} - x \, \ left (\ frac {1} { 3} - x \, \ left (\ frac {1} {4} - x \, \ left (\ frac {1} {5} - \ ldots \ right) \ right) \ right) \ right) \ right) \ quad {\ rm para} \ quad \ left | x \ right | <1 \, \.!$

Para obter uma melhor taxa de convergência, o seguinte identidade pode ser utilizado.

$\ Ln (x) = \ ln \ left (\ frac {1} {y + 1-y} \ right)$	$= 2 \, y \, \ left (\ frac {1} {1} + \ frac {1} {3} y ^ {2} + \ frac {1} {5} y ^ {4} + \ frac { 1} {7} y ^ {6} + \ frac {1} {9} y ^ {8} + \ ldots \ right)$
	$= 2 \, y \, \ left (\ frac {1} {1} + y ^ {2} \, \ left (\ frac {1} {3} + y ^ {2} \, \ left (\ frac {1} {5} + y ^ {2} \, \ left (\ frac {1} {7} + y ^ {2} \, \ left (\ frac {1} {9} + \ ldots \ right) \ right) \ right) \ right) \ right)$

desde que Y = (x -1) / (x + 1) e x> 0.

Para ln (x) em que x> 1, quanto mais próximo o valor de x é 1, mais rápida será a velocidade de convergência. As identidades associadas com o logaritmo pode ser aproveitado para explorar esta:

$\ Ln (123.456) \!$	$= \ Ln (1,23456 \ times 10 ^ 2) \, \!$
	$= \ Ln (1,23456) + \ ln (10 ^ 2) \, \!$
	$= \ Ln (1,23456) + 2 \ times \ ln (10) \, \!$
	$\ approx \ ln (1,23456) + 2 \ times 2,3025851 \, \!$

Tais técnicas foram usadas antes calculadoras, referindo-se a tabelas numéricas e realizar manipulações tais como aqueles acima.

Alta precisão

Para calcular o logaritmo natural com muitos dígitos de precisão, a abordagem da série de Taylor não é eficiente, pois a convergência é lenta. Uma alternativa é usar o método de Newton para inverter a função exponencial, cuja série converge mais rapidamente.

Uma alternativa para o cálculo de uma precisão extremamente elevada, é a fórmula

$\ Ln x \ approx \ frac {\ pi} {2 M (1,4 / s)} - m \ ln 2$

em que M denota o aritmética-geométrico médio e

$s = x \, 2 ^ m> 2 ^ {P / 2},$

com m escolhida de modo que os bits de p de precisão é alcançada. Na verdade, se este método é usado, Newton inversão do logaritmo natural pode ser usado por outro lado para calcular a função exponencial de forma eficiente. (As constantes de ln 2 e π pode ser pré-calculado para a precisão desejada utilizando qualquer um dos vários conhecidos série rapidamente convergente.)

Complexidade computacional

O complexidade computacional de calcular o logaritmo natural (utilizando a média aritmética-geométrica) é O (H (n) ln n). Aqui N é o número de dígitos de precisão em que o logaritmo natural é a de ser avaliadas e H (n), é a complexidade computacional da multiplicação de dois números de n quatro dígitos.

Logaritmos complexos

A função exponencial pode ser estendido para uma função que dá um número complexo como E ^X para qualquer número arbitrário complexo x; basta usar a série infinita com x complexo. Esta função exponencial pode ser invertido para formar um logaritmo complexo que exibe a maior parte das propriedades do logaritmo comum. Há duas dificuldades: não tem x e ^x = 0; e verifica-se que o e ^{2 πi} = 1 = e ^0. Desde a propriedade multiplicativa ainda trabalha para a função exponencial complexa, e ^z = e ^{z 2 nπi,} para todo z complexo e inteiros n.

Assim, o logaritmo não pode ser definido para o conjunto do plano complexo , e, mesmo assim, é multi-avaliado - qualquer logaritmo complexo pode ser transformada em um logaritmo "equivalente" pela adição de qualquer múltiplo inteiro de 2 πi à vontade. O logaritmo complexo só pode ser de valor único no plano de corte . Por exemplo, i ln = 1/2 ou 5/2 πi πi ou -3/2 πi, etc .; e, embora i ⁴ = 1, 4 log i pode ser definida como dois πi, ou 10 πi ou -6 πi, e assim por diante.

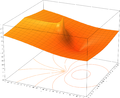
A representação gráfica da função de logaritmo natural no plano complexo (sucursal principal)
z = Re (ln (x + iy))
z = | Im (ln (x + iy)) |
Z = | ln (x + iy) |
Sobreposição dos três gráficos anteriores

Retirado de " http://en.wikipedia.org/w/index.php?title=Natural_logarithm&oldid=206770613 "

Home Page - YouTube Channel