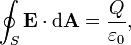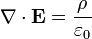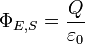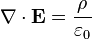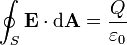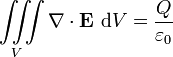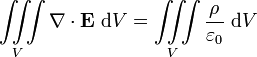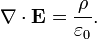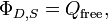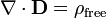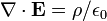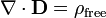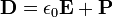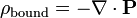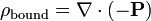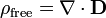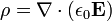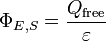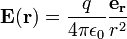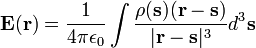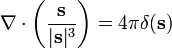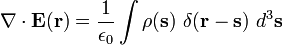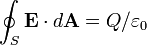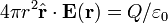A lei de Gauss

Eletromagnetismo
Eletricidade Magnetismo
Eletrostática Carga elétrica Eletricidade estática Campo elétrico Condutor Insulator Triboelectricity A descarga eletrostática Indução A lei de Coulomb A lei de Gauss Fluxo elétrico / energia potencial Momento de dipolo elétrico Densidade polarização
Magnetostática A lei de Ampère Campo magnético Magnetização O fluxo magnético Lei de Biot-Savart Momento de dipolo magnético A lei de Gauss para o magnetismo
Eletrodinâmica Lei da força de Lorentz Indução eletromagnética A lei de Faraday A lei de Lenz Corrente de deslocamento As equações de Maxwell Campo eletromagnético Radiação eletromagnética Maxwell tensor Poynting vector Potencial de Liénard-Wiechert Equações de Jefimenko Eddy atual
Rede elétrica Corrente elétrica Potencial elétrico Tensão Resistência A lei de Ohm Circuito em série Circuito paralelo Corrente contínua Corrente alternada Força eletromotiva Capacidade Indutância Impedância Cavidades de ressonância Waveguides
Formulação covariante Tensor eletromagnética ( tensor de tensão-energia) Quatro atual Electromagnética de quatro potencial
Os cientistas Ampère Coulomb Faraday Gauss Heaviside Henry Hertz Lorentz Maxwell Tesla Volta Weber Ørsted

Em física , "lei, também conhecido como Gauss Gauss teorema fluxo, é uma lei relativa à distribuição de carga elétrica para o resultante campo eléctrico . A lei de Gauss afirma que:

A lei foi formulada por Carl Friedrich Gauss em 1835, mas não foi publicado até 1867. É uma das quatro equações de Maxwell que formam a base de eletrodinâmica clássica, o outro ser três A lei de Gauss para o magnetismo, Lei de indução de Faraday, e A lei de Ampère com a correção de Maxwell. A lei de Gauss pode ser utilizado para derivar a lei de Coulomb , e vice-versa.

A lei de Gauss pode ser expressa de forma integrante:

onde o lado esquerdo da equação é um integral de superfície que denota o fluxo eléctrico através de uma superfície fechada S, e o lado direito da equação é a carga total fechada por S dividida pela constante elétrica.

A lei de Gauss também tem uma forma diferencial:

onde ∇ · E é o divergência do campo eléctrico , e é o ρ cobrar densidade.

As formas integral e diferencial estão relacionados pela teorema da divergência, também chamado de teorema de Gauss. Cada uma destas formas pode também ser expressa de duas maneiras: em termos de uma relação entre o campo eléctrico E e a carga eléctrica total, ou em termos de elétrica campo de deslocamento D ea carga elétrica livre.

A lei de Gauss tem uma semelhança matemática perto com uma série de leis em outras áreas da física, tais como A lei de Gauss para o magnetismo e A lei de Gauss para a gravidade. Na verdade, qualquer " lei do inverso do quadrado "pode ser formulado de uma maneira semelhante à lei de Gauss: Por exemplo, a lei de Gauss em si é essencialmente equivalente ao inverso do quadrado da lei de Coulomb , e a lei de Gauss em função da gravidade é essencialmente equivalente ao inverso do quadrado Lei da gravidade de Newton.

A lei de Gauss pode ser usado para demonstrar que todos os campos eléctricos dentro de um Gaiola de Faraday tem uma carga elétrica. A lei de Gauss é algo de um análogo elétrica de A lei de Ampère, que lida com o magnetismo.

Em termos de carga total

Forma integral

Para um volume V com a superfície S, a lei de Gauss afirma que

Φ onde _{E, S} é a fluxo elétrico através de S, Q é carga total dentro de V, e ε ₀ é o constante elétrica. O fluxo eléctrico é dada por um superfície integral sobre S:

onde E é o campo eléctrico, d A é um vector que representa um elemento infinitesimal de área , e · representa o produto de ponto ..

Aplicando a forma integral

Se o campo eléctrico é conhecido em toda a parte, a lei de Gauss torna muito fácil, em princípio, para encontrar a distribuição da carga eléctrica: O custo de uma dada região pode ser deduzida através da integração do campo eléctrico para encontrar o fluxo.

No entanto, muito mais frequentemente, é o problema inverso que tem de ser resolvido: A distribuição de carga eléctrica é conhecido, e o campo eléctrico tem de ser calculada. Isso é muito mais difícil, uma vez que se você sabe o fluxo total através de uma dada superfície, que dá quase nenhuma informação sobre o campo elétrico, que (para todos que você conhece) poderia entrar e sair da superfície em padrões arbitrariamente complicadas.

Uma excepção é se há alguns simetria na situação, que determina que o campo eléctrico passa através da superfície de uma maneira uniforme. Então, se o fluxo total for conhecida, o próprio campo pode deduzir-se em todos os pontos. Exemplos comuns de simetrias que se prestam a lei de Gauss incluem simetria cilíndrica, planar simetria, e simetria esférica. Veja o artigo Superfície de Gauss para exemplos onde estas simetrias são exploradas para calcular os campos eléctricos.

Formulário diferencial

Em forma diferencial , a lei de Gauss afirma:

onde ∇ · denota divergência, E é o campo eléctrico, e ρ é o total de eletricidade cobrar densidade (incluindo taxa de tanto livre e ligado) e ε ₀ é a constante elétrica. Este é matematicamente equivalentes à forma integrante, por causa da teorema da divergência.

Equivalência de formas integral e diferencial

As formas integral e diferencial são matematicamente equivalentes, pelo teorema da divergência. Aqui é o argumento mais especificamente:

A forma integral da lei de Gauss é:

S para qualquer superfície fechada contendo carga Q. Pelo teorema da divergência, esta equação é equivalente a:

para qualquer volume V, que contém carga Q. Por a relação entre a carga e densidade de carga, esta equação é equivalente a:

para qualquer volume V. Para que esta equação para ser simultaneamente verdadeiro para todos os possíveis volume V, é necessário (e suficiente) para os integrandos para ser igual em toda parte. Portanto, esta equação é equivalente a:

Assim, as formas integral e diferencial são equivalentes.

Em termos de carga livre

Livre versus carga acoplado

A carga elétrica que surge nas situações mais simples de livros didáticos seria classificado como "carga livre" -para exemplo, a carga que é transferida em eletricidade estática, ou a carga em um placa de capacitor. Em contraste, "carga ligado" surge apenas no contexto de dielétrico (polarizáveis) materiais. (Todos os materiais são, até certo ponto polarizável.) Quando tais materiais são colocados num campo eléctrico externo, os electrões permanecem ligados aos respectivos átomos, mas deslocar uma distância microscópica em resposta ao campo, de modo que eles são mais de um lado do átomo do que o outro. Todos esses deslocamentos microscópicas adicionar até dar uma distribuição de carga líquida macroscópica, e isso constitui a "carga ligado".

Embora microscopicamente, toda a carga é fundamentalmente o mesmo, muitas vezes há razões práticas para querer tratar carga ligada de forma diferente de carga livre. O resultado é que o mais direito "fundamentais" de Gauss, em termos de E, é por vezes colocado na forma equivalente a seguir, que é em função de D, e apenas a carga livre.

Forma integral

Esta formulação da lei de Gauss indica que, para qualquer volume V no espaço, com superfície S, a seguinte equação detém:

onde Φ _{D, S} é o fluxo do deslocamento elétrico campo D através de S, e Q _livre é a carga livre contido em V. O fluxo Φ _{D, S} é definida de forma análoga ao fluxo Φ _{E, S} do campo eléctrico E através de S. Especificamente, é dado pelo integral de superfície

Formulário diferencial

A forma diferencial da lei de Gauss, envolvendo apenas carga livre, afirma:

onde ∇ · D é a divergência do campo de deslocamento elétrico e ρ _livre é a densidade de carga elétrica livre.

A forma diferencial e forma integral são matematicamente equivalentes. A prova envolve principalmente o teorema da divergência.

Equivalência de total e livre declarações de carga

A prova de que as formulações da lei de Gauss em termos de carga livres são equivalentes para as formulações envolvendo carga total.

Nesta prova, vamos mostrar que a equação é equivalente à equação Note que estamos apenas lidando com as formas diferenciais, e não os formulários integrais, mas que é suficiente uma vez que o diferencial e formas integrais são equivalentes em cada caso, pelo teorema da divergência. Nós introduzimos o polarização P densidade, que tem a seguinte relação para E e D: e a seguinte relação à carga limite: Agora, considere as três equações: O aspecto chave é que a soma das duas primeiras equações é a terceira equação. Isto completa a prova: A primeira equação é verdade, por definição, e, por conseguinte, a segunda equação é verdadeiro Se e só se a terceira equação é verdadeiro. Assim, os segundo e terceiro equações são equivalentes, que é o que queria provar.

Em materiais lineares

Em homogêneo, isotrópico, não dispersivo, materiais lineares, há um agradável, simples relação entre E e D:

onde ε é a permitividade do material. Nestas circunstâncias, há ainda um outro par de formulações equivalentes da lei de Gauss:

Relação com a lei de Coulomb

Derivando a lei de Gauss da lei de Coulomb

A lei de Gauss pode ser derivada da lei de Coulomb , que afirma que o campo elétrico devido a uma estacionária carga pontual é:

onde

e _r é o radial vector unitário,

r é o raio, | R |,

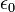é o constante eléctrico,

q é a carga da partícula, que é assumida para ser localizado no origem.

Usando a expressão da lei de Coulomb, obtemos o campo total de R usando um integrante para somar o campo em r devido à carga infinitesimal para o outro ponto s no espaço, para dar

onde 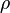é a densidade de carga. Se tomarmos a divergência de ambos os lados da equação em relação a R, e usar o teorema conhecido

onde δ (s) é a Delta de Dirac, o resultado é

Utilizando o " peneirar propriedade "da função delta de Dirac, chegamos a

que é a forma diferencial da lei de Gauss, como desejado.

Observe que, como a lei de Coulomb só se aplica aos encargos fixos, não há razão para esperar que a lei de Gauss para segurar a um custo com base em sozinhos essa derivação em movimento. Na verdade, a lei de Gauss se sustenta por cargas em movimento, e neste aspecto a lei de Gauss é mais geral do que a lei de Coulomb.

Derivando a lei de Coulomb da lei de Gauss

A rigor, a lei de Coulomb não pode ser derivada da lei de Gauss sozinho, uma vez que a lei de Gauss não dá qualquer informação sobre a onda de E (ver Helmholtz e decomposição A lei de Faraday). No entanto, a lei de Coulomb pode ser comprovado a partir da lei de Gauss se for assumido, além disso, que a partir de um campo eléctrico carga pontual é esfericamente simétrica (essa suposição, como a lei de Coulomb em si, é exatamente verdade, se a carga está parado, e aproximadamente verdadeira se a carga estiver em movimento).

Tomando S na forma integral da lei de Gauss para ser uma superfície esférica de raio r, centrado na carga pontual Q, temos

No pressuposto de simetria esférica, o integrando é uma constante que pode ser levado para fora do integrante. O resultado é

onde 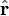é um vetor unitário apontando radialmente afastando-se da acusação. Novamente por simetria esférica, pontos E na direção radial, e por isso se

que é essencialmente equivalente à lei de Coulomb. Assim, o inverso do quadrado dependência direito do campo elétrico na lei de Coulomb decorre do direito do Gauss.