Indutância
Sobre este escolas selecção Wikipedia
Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. Clique aqui para saber mais sobre apadrinhamento de crianças.
| Eletromagnetismo |
|---|
 |
Eletrostática
|
Magnetostática
|
Eletrodinâmica
|
Rede elétrica
|
Formulação covariante Tensor eletromagnética ( tensor de tensão-energia)
|
Em eletromagnetismo e eletrônica , indutância é propriedade de um condutor através do qual uma mudança em corrente no condutor "induz" (cria) um Tensão ( força eletromotriz) em tanto o próprio (auto-indutância do condutor) e em quaisquer condutores nas proximidades (indutância mútua). Este efeito decorre de duas constatações fundamentais da física: Em primeiro lugar, que uma corrente constante cria um campo magnético estacionário ( A lei de Oersted) e em segundo lugar, que um campo magnético variável no tempo induz uma tensão em um condutor próximo ( Lei de indução de Faraday). A partir de A lei de Lenz, numa circuito eléctrico, uma corrente eléctrica através de uma mudança de circuito que tem indutância induz uma tensão proporcional que se opõe à mudança na corrente (auto-indutância). O campo variando neste circuito também pode induzir uma EMF em um circuito (indutância mútua) vizinho.
O termo 'indução' foi cunhado por Oliver Heaviside em fevereiro de 1886. É costume de usar o símbolo L para indutância, em honra do físico Heinrich Lenz. No Sistema SI da unidade de indutância é a henry, nomeado em homenagem ao cientista que descobriu indutância, Joseph Henry.
Para adicionar a indutância de um circuito, eléctrica ou componentes eletrônicos chamados indutores são utilizados, tipicamente constituído de espiras de fio para concentrar o campo magnético e de modo que o campo magnético é ligada ao circuito de mais do que uma vez.
A relação entre a auto-indutância L de um circuito elétrico em henries, tensão e corrente é
onde v denota a tensão em volts e i a corrente em amperes. A tensão através de um indutor é igual ao produto da sua indutância e a taxa de variação da corrente através dele.
Todos os circuitos práticos têm alguma indutância, o que pode proporcionar efeitos benéficos ou prejudiciais. Em um indutância do circuito sintonizado é usado para fornecer um circuito selectivo de frequência. Indutores práticos podem ser usados para fornecer a filtragem ou de armazenamento de energia no sistema. A indutância de um A linha de transmissão é uma das propriedades que determina a sua impedância característica; equilibrando a indutância e capacitância dos cabos é importante para a distorção-livre telegrafia e telefonia. A indutância de linhas de transmissão de energia de longo limita o poder AC que podem ser enviados sobre eles. Circuitos sensíveis, tais como e microfone cabos de rede de computadores podem usar construções de cabos especiais para limitar a indutância mútua entre os circuitos de sinais.
Na análise de circuitos
A generalização para o caso de K circuitos elétricos com correntes e tensões i m v m lê
Indutância aqui é uma matriz simétrica. A diagonal coeficientes L m, m são chamados coeficientes de auto-indutância, os elementos fora da diagonal são chamados coeficientes de indutância mútua. Os coeficientes de indutância são constantes, desde que nenhum material magnetizável com características não lineares está envolvido. Esta é uma consequência directa da linearidade das equações de Maxwell nos campos e a densidade de corrente. Os coeficientes de indutância tornar-se funções das correntes no caso não-linear, ver indutância não-linear .
Derivação da lei de Faraday de indutância
As equações de indutância acima são uma consequência de equações de Maxwell . Há uma derivação simples no caso importante de circuitos eléctricos que consistem em fios finos.
Considere-se um sistema de alças de fio K, cada um com uma ou várias voltas de arame. O ligação do fluxo de malha m é dada pela
Aqui N m denota o número de voltas no circuito m, Φ sou o fluxo magnético através deste circuito, e L m, n são algumas constantes. Esta equação seguinte a partir de A lei de Ampere - campos magnéticos e fluxos são funções lineares das correntes. Por Lei de indução de Faraday temos
onde v m indica a tensão induzida no circuito de m. Isto está de acordo com a definição acima de indutância se os coeficientes L m, n são identificados com os coeficientes de indutância. Porque os totais correntes N n i n contribuir para Φ m segue-se também que a L m, n é proporcional ao produto de espiras N N n m.
Indutância e energia do campo magnético
Multiplicando a equação para v m acima com i m dt e somando m dá a energia transferida para o sistema no intervalo de tempo dt,
Este deve concordar com a mudança da energia magnética W campo causado pelas correntes. A condição de integrabilidade
requer G m, n = L n, m. A matriz de indutância L m, n, assim, é simétrica. O integrante da transferência de energia é a energia do campo magnético em função das correntes,
Esta equação também é uma consequência directa de a linearidade das equações de Maxwell. É útil para associar mudando correntes elétricas com um acúmulo ou redução de energia campo magnético. A transferência de energia correspondente requer ou gera uma tensão. Uma analogia mecânica no caso K = 1 com energia do campo magnético (1/2) Li 2 é um corpo de massa M, a velocidade e energia cinética u (1/2) 2 MU. A taxa de variação da velocidade (atual) multiplicada com a massa (indutância) requer ou gera uma força (tensão).
Indutores acoplados

Indutância mútua ocorre quando a mudança na corrente em um indutor induz uma voltagem num outro indutor nas proximidades. É importante que o mecanismo pelo qual Transformadores de trabalho, mas também pode causar o acoplamento indesejado entre os condutores de um circuito.
A indutância mútua, M, é também uma medida do acoplamento entre dois indutores. A indutância mútua pelo circuito i no circuito j é dada pelo integral duplo Fórmula Neumann, ver técnicas de cálculo
A indutância mútua também tem a relação:
onde
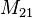 é a indutância mútua, e o subscrito especifica a relação da tensão induzida na bobina 2, devido à corrente na bobina 1.
é a indutância mútua, e o subscrito especifica a relação da tensão induzida na bobina 2, devido à corrente na bobina 1. - 1 N é o número de espiras na bobina 1,
- 2 N é o número de espiras na bobina 2,
- P 21 é a permeabilidade do espaço ocupado pelo fluxo.
A indutância mútua também tem um relacionamento com o coeficiente de acoplamento. O coeficiente de acoplamento é sempre entre 1 e 0, e é uma forma conveniente para especificar a relação entre uma determinada orientação de indutores com indutância arbitrária:
onde
- k é o coeficiente de acoplamento e 0 ≤ k ≤ 1,
- L1 é a indutância da primeira bobina, e
- 2 L é a indutância da segunda bobina.
Uma vez que a indutância mútua M é determinada a partir deste factor, pode ser utilizado para prever o comportamento de um circuito de:
onde
- V 1 é a tensão através do indutor de interesse,
- L1 é a indutância do indutor de interesse,
- I d 1 / d t é o derivado, em função do tempo, da corrente através do indutor de interesse,
- I d 2 / d t é o derivado, em função do tempo, da corrente através do indutor, que é acoplado ao primeiro indutor, e
- M é a indutância mútua.
O sinal de subtracção surge por causa da sensação da corrente I 2 foi definido no diagrama. Com ambas as correntes definido indo para os pontos do sinal de M será positivo.
Quando um indutor está intimamente acoplado a um outro indutor, através de indutância mútua, tal como numa do transformador, as tensões, correntes, e número de voltas pode ser relacionados da seguinte forma:
onde
- S V é a tensão através do indutor secundário,
- V p é a tensão através do indutor primário (o que está ligado a uma fonte de alimentação),
- N s é o número de espiras do indutor secundário em, e
- N p é o número de espiras do indutor primário em.
Por outro lado o atual:
onde
- I S representa a corrente através do indutor secundário,
- I, p é a corrente através do indutor primário (o que está ligado a uma fonte de alimentação),
- N s é o número de espiras do indutor secundário em, e
- N p é o número de espiras do indutor primário em.
Note-se que a potência através de um indutor é o mesmo que a potência através do outro. Observe também que estas equações não funcionam se ambos os transformadores são forçados (com fontes de energia).
Quando ambos os lados do transformador é um circuito sintonizado, a quantidade de indutância mútua entre os dois enrolamentos determina a forma da curva de resposta de frequência. Embora não há limites são definidos, esta é muitas vezes referida como loose-, crítico-, e o excesso de acoplamento. Quando dois circuitos sintonizados são fracamente acoplada através de indutância mútua, a largura de banda será estreita. Como a quantidade de indutância mútua aumenta, a largura de banda continua a crescer. Quando a indutância mútua é aumentada para além de um ponto crítico, o pico na curva de resposta começa a cair, e a frequência central irá ser atenuada mais fortemente do que as suas bandas laterais directos. Isto é conhecido como overcoupling.
Técnicas de cálculo
No caso mais geral, a indutância pode ser calculada a partir das equações de Maxwell. Muitos casos importantes podem ser resolvidos utilizando simplificações. Onde as correntes de alta frequência são considerados, com efeito de pele, as densidades de corrente e do campo magnético de superfície pode ser obtida através da resolução da equação de Laplace. Sempre que os condutores são fios finos, auto-indutância ainda depende do raio de arame e a distribuição da corrente no fio. Esta distribuição de corrente é aproximadamente constante (na superfície ou no volume do fio) para um raio muito mais pequeno do que o fio de outras escalas de comprimento.
Indutância mútua de dois loops de arame
A indutância mútua por um circuito filamentar i em um circuito filamentar j é dada pelo integral duplo Fórmula Neumann
O símbolo denota a 0 μ magnético constante (4π × 10 -7 H / m), C i e C j são as curvas gerado pelos fios, R ij é a distância entre dois pontos. Veja uma derivação dessa equação.
A auto-indutância de uma alça de arame
Formalmente, a auto-indutância de uma alça de arame seria dada pela equação acima, com i = j. O problema, no entanto, é que 1 / R torna-se agora infinito, tornando-se necessário levar a um fio finito raio e a distribuição da corrente no fio em conta. Restam a contribuição da integral sobre todos os pontos com | R |> a termo / 2 e uma correção,
Aqui, um raio e l designam e comprimento do fio, e Y é uma constante que depende da distribuição da corrente no fio: Y = 0, quando a corrente flui na superfície do fio ( efeito de pele), Y = 1/4 quando a corrente é homogênea em toda a fio. Esta aproximação é preciso, quando os fios são longos em comparação com as suas dimensões da secção transversal.
Método de imagens
Em alguns casos, diferentes distribuições actuais gerar o campo magnético na mesma secção de algum espaço. Este fato pode ser usado para relacionar auto indutâncias ( método de imagens). Como um exemplo, considere os dois sistemas:
- Um fio a uma distância d / 2 em frente de uma parede de condutor perfeito (o que é o retorno)
- Dois fios paralelos à distância d, com corrente oposta
O campo magnético dos dois sistemas coincide (em meio espaço). A energia do campo magnético e a indutância do segundo sistema é, portanto, duas vezes maior que a do primeiro sistema.
Relação entre indutância e capacitância
Indutância por comprimento L 'e capacitância por unidade de comprimento C 'estão relacionados uns aos outros, no caso especial de linhas de transmissão composto por dois condutores perfeitos paralelas de seção transversal arbitrária, mas constante,
Aqui ε e μ denotar constante dielétrica e permeabilidade magnética do meio dos condutores são incorporados em. Não há nenhum campo eléctrico e magnético no interior dos condutores (completo efeito de pele de alta frequência). A corrente flui para baixo sobre uma linha e retorna por outro. Sinais irá propagar ao longo da linha de transmissão a uma velocidade de radiação electromagnética na forma não-condutora que envolve os condutores.
A auto-indutância de circuitos eléctricos simples em ar
A auto-indutância de muitos tipos de circuitos eléctricos pode ser dada de forma fechada. Exemplos são listados na tabela.
| Tipo | Indutância | Comente |
|---|---|---|
| Camada única solenóide | 
|  : Número de voltas : Número de voltas R: raio l: Comprimento w = r / l   : Integrais elípticas : Integrais elípticas |
| Cabo coaxial, alta freqüência | 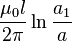 | um 1: Raio exterior um: raio interno l: Comprimento |
| Laço Circular |  | r: loop raio um: raio de arame |
| Retângulo |  | b, d: comprimento Border d >> a, b >> um um: raio de arame |
| Par de paralelo fios |  | um: raio de arame d: Distância, d ≥ 2-A l: Comprimento de par |
| Par de paralelo fios, de alta freqüência |  | um: raio de arame d: Distância, d ≥ 2-A l: Comprimento de par |
| Fio paralelo ao perfeitamente realização de parede |  | um: raio de arame d: Distância, d ≥ um l: Comprimento |
| Fio paralelo ao realização de parede, alta freqüência | 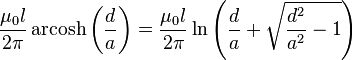 | um: raio de arame d: Distância, d ≥ um l: Comprimento |
O símbolo denota a 0 μ constante magnética (4π × 10 -7 H / m). Para altas freqüências a corrente elétrica flui na superfície do condutor ( efeito de pele), e, dependendo da geometria, por vezes, é necessário distinguir indutâncias de baixa e alta frequência. Este é o propósito da constante Y: Y = 0, quando a corrente é distribuída uniformemente sobre a superfície do arame a (efeito de pele), Y = 1/4, quando a corrente é distribuído uniformemente sobre a secção transversal do fio. No caso de alta freqüência, se aproximam uns dos outros condutores, uma corrente de rastreio adicional flui em sua superfície, e expressões que contêm Y se tornar inválido.
Indutância com simetria física
Indutância de um solenóide
A solenóide é um longo e fino da bobina, isto é, uma bobina cujo comprimento é muito maior do que o diâmetro. Sob estas condições, e sem qualquer material magnético utilizado, o A densidade do fluxo magnético 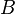 no interior da bobina é praticamente constante e é dada pela
no interior da bobina é praticamente constante e é dada pela
onde  é o magnético constante,
é o magnético constante,  o número de voltas,
o número de voltas, 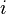 a corrente e
a corrente e 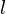 o comprimento da bobina. Ignorando efeitos finais do fluxo magnético total através da serpentina é obtida multiplicando a densidade de fluxo
o comprimento da bobina. Ignorando efeitos finais do fluxo magnético total através da serpentina é obtida multiplicando a densidade de fluxo 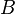 por a área da secção transversal
por a área da secção transversal  e o número de voltas
e o número de voltas  :
:
Quando isto é combinado com a definição de indutância,
segue-se que a indutância de um solenóide é dada por:
Uma mesa de indutância para solenóides curtas de vários diâmetro para rácios de comprimento foi calculada pela Dellinger, Whittmore, e Ould
Este, e a indutância de formas mais complicadas, pode ser derivada a partir de equações de Maxwell . Para bobinas rígidas de núcleo de ar, indutância é uma função da geometria da bobina e do número de voltas, e é independente de corrente.
Uma análise semelhante aplica-se a um solenóide com um núcleo magnético, mas apenas se o comprimento da bobina é muito maior do que o produto da permeabilidade relativa do núcleo magnético e o diâmetro. Isso limita a análise simples de núcleos de baixa permeabilidade, ou extremamente longos solenóides finas. Embora raramente útil, as equações são,
onde  a permeabilidade relativa do material no interior do solenóide,
a permeabilidade relativa do material no interior do solenóide,
de onde resulta que a indutância de um solenóide é dada por:
onde N é elevado ao quadrado, devido à definição de indutância.
Note-se que uma vez que a permeabilidade dos materiais ferromagnéticos, com alterações do fluxo magnético aplicado, a indutância de uma bobina com um núcleo ferromagnético geralmente variará com corrente.
Indutância de uma linha coaxial
Deixe o condutor interno tem raio  e permeabilidade
e permeabilidade  , Deixe o dielétrico entre o condutor interno e externo têm permeabilidade
, Deixe o dielétrico entre o condutor interno e externo têm permeabilidade  , E deixar que o condutor externo tem raio interno
, E deixar que o condutor externo tem raio interno  , Raio externo
, Raio externo  , E permeabilidade
, E permeabilidade  . Assume-se que uma corrente DC
. Assume-se que uma corrente DC  fluxos em sentidos opostos nos dois condutores, com densidade de corrente uniforme. O campo magnético gerado por estas correntes aponta na direcção azimutal e é uma função do raio
fluxos em sentidos opostos nos dois condutores, com densidade de corrente uniforme. O campo magnético gerado por estas correntes aponta na direcção azimutal e é uma função do raio  ; pode ser calculado usando o A lei de Ampère:
; pode ser calculado usando o A lei de Ampère:
O fluxo por comprimento 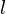 na região entre os condutores pode ser calculado através da elaboração de uma superfície que contém o eixo:
na região entre os condutores pode ser calculado através da elaboração de uma superfície que contém o eixo:
Dentro dos condutores, L pode ser calculado igualando a energia armazenada no indutor,  , Com a energia armazenada no campo magnético:
, Com a energia armazenada no campo magnético:
Para uma geometria cilíndrica com nenhuma 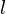 dependência, a energia por unidade de comprimento é
dependência, a energia por unidade de comprimento é
onde 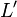 é a indutância por unidade de comprimento. Para o condutor interno, a integral sobre a mão-lado-direito é
é a indutância por unidade de comprimento. Para o condutor interno, a integral sobre a mão-lado-direito é  ; para o condutor exterior é
; para o condutor exterior é 
Resolvendo para 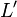 e somando os termos para cada região juntos dá uma indutância total por unidade de comprimento:
e somando os termos para cada região juntos dá uma indutância total por unidade de comprimento:
No entanto, para uma aplicação típica linha coaxial estamos interessados em passar sinais (não-DC) em freqüências para o qual a resistiva efeito de pele não pode ser negligenciada. Na maioria dos casos, os termos condutores interior e exterior são negligenciável, caso em que se pode aproximar
Análise de circuitos Phasor e impedância
Uso fasores, o equivalente impedância de uma indutância é dada por:
onde
- j é a unidade imaginária ,
- L é a indutância,
- ω = 2πf é a freqüência angular,
- f é a frequência e
- ωL = X L é o indutivo reactance.
Indutância não-linear
Muitos indutores fazer uso de materiais magnéticos . Estes materiais ao longo de um grande intervalo suficiente exibem uma permeabilidade não linear com efeitos tais como saturação. Isto, por sua vez, torna-a indutância resultante em função da corrente aplicada. Lei de Faraday, mas ainda mantém indutância é ambígua e é diferente se você está no cálculo dos parâmetros de circuito ou fluxos magnéticos.
A indutância secante ou de grandes sinais é usada em cálculos do fluxo. Ela é definida como:
O diferencial ou pequenos sinais indutância, por outro lado, é utilizado no cálculo da tensão. Ela é definida como:
A tensão de circuito para um indutor não-linear é obtida através da indutância diferencial, como mostrado pela Lei de Faraday e o regra da cadeia de cálculo.
Há definições semelhantes para indutâncias mútuas não-lineares.

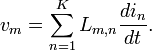






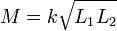


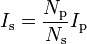


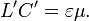

 para w << 1
para w << 1  para w >> 1
para w >> 1