Homeomorfismo

A deformação permanente entre um caneca de café e uma rosquinha ilustrando que eles são homeomorphic. Mas não é necessário ser uma deformação contínua durante dois espaços para ser homeomorfos.

Na matemática campo da topologia , um homeomorfismo ou isomorfismo topológico (do grego palavras homoios = semelhante e μορφή (morphe) = = forma formulário (deformação Latina de morphe)) é um especial isomorfismo entre espaços topológicos que respeita propriedades topológicas. Dois espaços com um homeomorfismo entre eles são chamados homeomorphic. De um ponto de vista topológico eles são os mesmos.

Grosso modo, um espaço topológico é um geométrico objeto eo homeomorfismo é um alongamento e flexão contínua do objeto em uma nova forma. Assim, um quadrado e um círculo são homeomorfos um ao outro, mas uma esfera e um doughnut não são. Uma piada tantas vezes repetida é que topologists não pode dizer a xícara de café a partir do qual eles estão bebendo da filhós eles estão comendo, uma vez que um donut suficientemente flexível poderia ser reformulado para a forma de um copo de café, criando uma covinha e progressivamente ampliando- , enquanto encolhendo o furo em uma alça.

Intuitivamente, um homeomorfismo Mapas de pontos no primeiro objeto que são "fecham juntos" para pontos no segundo objeto que estão juntos, e pontos no primeiro objeto que não estão juntos aos pontos no segundo objeto que não estão juntos. A topologia é o estudo dessas propriedades de objetos que não mudam quando homeomorfismos são aplicadas.

Definição

A função f entre dois topológicos espaços X e Y é chamado um homeomorphism se ele tem as seguintes propriedades:

• f é um bijection ( 1-1 e para),
• f é contínua,
• a função inversa f ^-1 é contínua (f é uma mapeamento aberto).

Se esta função exista, dizemos X e Y são homeomorphic. A auto-homeomorfismo é um homeomorfismo de um espaço topológico e ela própria. Os homeomorfismos formar uma relação de equivalência na classe de todos os espaços topológicos. O resultado classes de equivalência são chamados de classes homeomorfismo.

Exemplos

A trevo nó é homeomorfo a um toro . Enquanto isto pode parecer ilógico, em quatro dimensões podem facilmente ser deformadas continuamente.

• A unidade de 2- ² do disco D e a quadrado unitário em R ² são homeomorphic.

• O aberto intervalo (-1, 1) é homeomorfo ao números reais R.

• O produto espaço S ¹ × S ¹ e a dois dimensionais toro são homeomorphic.

• Cada isomorfismo uniforme e isomorfismo isométrico é um homeomorfismo.

• Qualquer 2-esfera com um único ponto removido é homeomorfo ao conjunto de todos os pontos em R ² (um 2-dimensional de avião ).

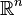• e 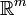não são para homeomorphic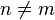

Propriedades

• Dois espaços homeomorfos compartilham a mesma propriedades topológicas. Por exemplo, se um deles é compacto , então o outro é assim; Se um deles é ligado, então o outro é assim; Se um deles é Hausdorff, então o outro é assim; seu grupos de homologia vai coincidir. Note, porém, que este não se estende às propriedades definidas através de um métrica; há espaços métricos que são homeomorphic mesmo que um deles é e completar o outro não é.

• Um homeomorphism é simultaneamente um mapeamento aberta e um mapeamento fechado, que é ele mapeia conjuntos abertos para abrir conjuntos e conjuntos fechados para conjuntos fechados.

• Cada auto-homeomorfismo em pode ser estendido para uma auto-homeomorphism de todo o disco 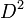( Truque de Alexandre).

Discussão informal

O critério intuitivo de alongamento, dobra, corte e colagem de volta juntos preciso uma certa quantidade de prática de aplicar corretamente - pode não ser óbvia a partir da descrição acima que deformando um segmento de linha para um ponto é inadmissível, por exemplo. Assim, é importante perceber que é a definição formal dada acima que conta.

Esta caracterização de um homeomorphism muitas vezes leva a uma confusão com o conceito de homotopy , que na verdade é definida como uma deformação contínua, mas a partir de uma função para outra, em vez de um espaço para outro. No caso de um homeomorfismo, prevendo uma deformação contínua é uma ferramenta mental para manter o controle de quais pontos no espaço X correspondem a que aponta em Y - um apenas os segue como X deforma. No caso de homotopy, a deformação contínua a partir de um mapa para o outro é essencial, e que também é menos restritiva, dado que nenhum dos mapas envolvidas necessidade de ser um-para-um ou em. Homotopia leva a uma relação em espaços: equivalência de homotopia .

Não é um nome para o tipo de deformação envolveu em visualizar uma homeomorphism. É (exceto quando o corte e regluing são obrigatórios) uma isotopia entre a mapa identidade em X eo homeomorfismo de X para Y.