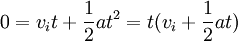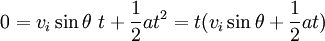Cinemática

Assuntos Relacionados: Matemática

Informações de fundo

Crianças SOS feita esta seleção Wikipedia ao lado de outros recursos escolas . Clique aqui para mais informações sobre Crianças SOS.

Cinemática ( grego κινειν, kinein, para mover) é um ramo da dinâmica que descreve o movimento de objetos sem a consideração das massas ou forças que trazem para fora o movimento. Em contraste, cinética está preocupado com as forças e interações que produzem ou afetam o movimento.

A aplicação mais simples de cinemática é apontar partícula movimento ( cinemática translacionais ou cinemática lineares). A descrição de rotação ( cinemática rotacional ou cinemática angular) é mais complicada. O estado de um corpo rígido genérico pode ser descrita através da combinação de ambos translação e rotação cinemática ( cinemática de corpo rígido). Um caso mais complicado é a cinemática de um sistema de corpos rígidos, possivelmente ligados entre si por processos mecânicos articulações. A descrição cinemática de fluxo de fluido é ainda mais complicada, e não geralmente consideradas no contexto da cinemática.

Movimento de translação

Translacional ou curvilíneas cinemática é a descrição do movimento no espaço de um ponto ao longo de uma trajectória. Esta via pode ser linear, ou curva, como visto com projéctil movimento. Existem três conceitos básicos que são necessários para a compreensão movimento de translação:

O deslocamento é a distância mais curta entre dois pontos: a origem eo ponto de deslocados. A origem é (0,0) numa sistema que é definida pelo observador de coordenadas. Porque o deslocamento tem tanto magnitude (comprimento) e direcção, é uma vetor cujo ponto inicial é a origem eo ponto final é o ponto de deslocados.
A velocidade é a taxa de variação no deslocamento em relação ao tempo; que é o deslocamento de um ponto muda com o tempo. A velocidade é também um vector. Para uma velocidade constante, a cada unidade de tempo aumenta o comprimento do vector de velocidade (no mesmo sentido) para o deslocamento do ponto móvel. Velocidade Instantânea (a velocidade a um instante de tempo) é definida como $\ Vec v = \ frac {d \ vec s} {d t}$ , Onde ds é um infinitamente pequeno deslocamento e dt é um infinitamente pequeno período de tempo. Velocidade média (velocidade ao longo de um período de tempo) é definida como $\ Vec v = \ frac {\ Delta \ vec s} {\ Delta t}$ , Onde Ds é a variação no deslocamento e At é o intervalo de tempo durante o qual o deslocamento alterações.
A aceleração é a taxa de variação da velocidade em relação ao tempo. A aceleração é também um vector. Tal como acontece com a velocidade constante se a aceleração é, para cada unidade de tempo que o comprimento do vector de aceleração (na mesma direcção) é adicionado à velocidade. Se a variação da velocidade (um vector) é conhecido, a aceleração é paralelo a ele. Aceleração instantânea (a aceleração a um instante de tempo) é definida como $\ Vec a = \ frac {d \ vec v} {d t}$ , Onde dv é uma infinitamente pequena mudança na velocidade e dt é um infinitamente pequeno período de tempo. Média aceleração (a aceleração ao longo de um período de tempo) é definida como $\ Vec a = \ frac {\ Delta \ vec v} {\ Delta t}$ , Onde? V é a mudança na velocidade e Dt é o intervalo de tempo durante o qual as mudanças de velocidade.

Quando a aceleração é constante, é dito estar passando por movimento uniformemente acelerado. Se este for o caso, há quatro equações que podem ser utilizados para descrever o movimento de um objecto.

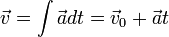$\ Vec v = \ int \ vec um dt = \ v_0 vec + \ vec uma t$ Aqueles que estão familiarizados com cálculo pode reconhecer isso como um problema de valor inicial. Porque aceleração (a) é uma constante, integrando-se com respeito ao tempo (t) faz uma mudança de velocidade. A adição deste à velocidade inicial (v ₀₎ dá a velocidade final (v).
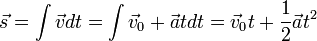$\ Vec s = \ int \ vec v dt = \ int \ v_0 vec + \ vec a dt = \ vec v_0 t + \ frac {1} {2} \ vec a ^ 2$ Usando a fórmula anterior, podemos substituir v para se chegar a esta equação, onde s é o deslocamento.
$\ Vec s = \ frac {\ v + \ vec v_0 vec} {2} t$ Utilizando a definição de um média, eo conhecimento que os tempos de velocidade média é igual a tempo de deslocamento, podemos chegar a esta equação.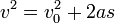
$v ^ 2 = v_0 ^ 2 + 2 um s$

Velocidade relativa

Para descrever o movimento de um objeto A em relação ao objeto O, quando sabemos como cada um está se movendo em relação ao objeto B, usamos a seguinte equação envolvendo vetores e adição de vetores:

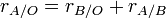
$r_ {A / S} = r_ {B / O} + {r_ A / B} \, \!$

A equação de movimento relativo acima afirma que o movimento de um em relação ao S é igual ao movimento de B em relação a O mais o movimento de um em relação a B.

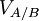Por exemplo, vamos Ann mover com velocidade $V_ {A}$ e deixar que se move com velocidade Bob $V_ {B}$ , A velocidade de cada dado em relação ao chão. Para encontrar o quão rápido Ann está se movendo em relação ao Bob (nós chamamos isso de velocidade $V_ {A / B}$ ), A equação acima dá:

$V_ {A} = V_ {B} {V_ + A / B} \, \! .$

Encontrar 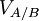$V_ {A / B}$ nós simplesmente reorganizar esta equação para obter:

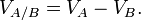
$V_ {A / B} = V_ {A} -V_ {B} \, \! .$

Em velocidades comparáveis à velocidade da luz , estas equações não são válidos. Eles são substituídos por equações derivadas de Einstein teoria da relatividade especial .

Exemplo: Rectilinear (1D) de movimento

Um objeto é acionado para cima, atinge o seu ápice, e, em seguida, começa sua descida sob uma aceleração constante.

Considere um objeto que é disparado diretamente para cima e cai de volta para o chão, para que sua trajetória está contido em uma linha reta. Se se adoptar a convenção de que o sentido ascendente é o sentido positivo, o objecto sofre uma aceleração constante de aproximadamente -9,81 m / s ^2. Portanto, o seu movimento pode ser modelado com as equações que regem o movimento uniformemente acelerado.

Por uma questão de exemplo, suponha que o objecto tem uma velocidade inicial de 50 m / s. Há várias questões interessantes cinemáticas podemos perguntar sobre o movimento da partícula:

Quanto tempo vai ser transportado por via aérea?

Para responder a esta pergunta, nós aplicamos a fórmula

$x_f - x_i = v_i t + \ frac {1} {2} a ^ 2.$

Uma vez que a questão solicita o período de tempo entre o objecto sair do chão e bater no chão sobre a sua queda, o deslocamento é zero.

$0 = v_i t + \ frac {1} {2} a ^ 2 = t (+ v_i \ frac {1} {2} at)$

Nós encontramos duas soluções para isso. A solução trivial diz que o tempo é zero; este é, na verdade, também é verdade, é o primeiro momento em que o deslocamento é zero: apenas quando se inicia o movimento. No entanto, a solução é de interesse

$t = - \ frac {2v_i} {a} = - \ frac {2} {* 50 - 9,81} = 10.2 \ s$

O que altitude que vai chegar antes de começar a cair?

Neste caso, usamos o facto de o objecto tem uma velocidade de zero no vértice da sua trajectória. Portanto, a equação é aplicável:

$v_f ^ 2 = v_i ^ 2 + 2-A (x_f - x_i)$

Se a origem do nosso sistema de coordenadas está no chão, em seguida, $x_i$ é zero. Então nós resolvemos para $x_f$ e substituir os valores conhecidos:

$x_f = \ frac {v_f ^ 2 - v_i ^ 2} {2} + um x_i = \ frac {0-50 ^ 2} {2} * -9,81 0 = 127,55 \ m$

Qual será a sua velocidade final ser quando se atinge o solo?

Para responder a esta pergunta, nós usamos o fato de que o objeto tem uma velocidade inicial igual a zero no ápice antes de começar a descida. Podemos usar a mesma equação que usamos para a última pergunta, utilizando o valor de 127,55 m para $x_i$ .

$v_f = \ sqrt {v_i ^ 2 + 2-A (x_f - x_i)} = \ sqrt {0 ^ 2 + 2 (-9,81) (0-127,55)} = 50 \ m / s$

Assumindo que este experimento foram realizadas em um vácuo (negando efeitos de arrasto), descobrimos que as velocidades finais e iniciais são iguais, um resultado que concorda com conservação de energia.

Exemplo: movimento do projétil (2D)

Um objeto disparou em um ângulo $\ Theta$ a partir do solo segue uma trajetória parabólica.

Suponha que um objeto não é acionado na vertical, mas é despedido em um ângulo $\ Theta$ a partir do solo. O objeto, então, seguir uma trajetória parabólica, e seu movimento horizontal pode ser modelado independentemente de seu movimento vertical. Suponha que o objeto é acionado a uma velocidade inicial de 50 m / s e 30 graus a partir da horizontal.

Até onde vai viajar antes de bater no chão?

O objecto experimenta uma aceleração de -9,81 ms ^-2 na direcção vertical e sem aceleração na direcção horizontal. Por conseguinte, o deslocamento horizontal é

$\ Delta x = x_f - x_i = v_i \ cos \ theta \ t + \ frac {1} {2} a ^ 2 = v_i \ cos \ theta \ t$

A fim de resolver esta equação, temos de encontrar t. Isto pode ser feito através da análise do movimento na direcção vertical. Se impusermos que o deslocamento vertical é zero, nós podemos usar o mesmo procedimento que fizemos para movimento retilíneo para encontrar t.

$0 = v_i \ sin \ theta \ t + \ frac {1} {2} a ^ 2 = t (v_i \ sin \ theta + \ frac {1} {2} at)$

Nós agora resolver para t e substituir esta expressão para a expressão original para o deslocamento horizontal. (Note-se a utilização do identidade trigonométrica $2 \ sin \ theta \ cos \ theta = \ sin 2 \ theta$ )

$\ Delta x = v_i \ cos \ theta \ left (\ frac {-2 v_i \ sin \ theta} {a} \ right) = - \ frac {v_i ^ 2 \ sin 2 \ theta} {a} = 220,93 \ m$

Movimento de rotação

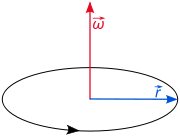
O vetor velocidade angular aponta para a rotação anti-horário e para baixo para a rotação no sentido horário, conforme especificado pelo regra da mão direita.

Cinemática de rotação é a descrição da rotação de um objecto e envolve a definição ea utilização das três quantidades seguintes:

Posição angular: Se um vector é definido como a distância orientada a partir do eixo de rotação para um ponto de um objecto, a posição angular desse ponto é o ângulo orientado $\ Theta$ a partir de um eixo de referência (por exemplo, os X-semiaxis positivos) para que vetor. Um ângulo orientado é um ângulo varrido torno de um eixo de rotação conhecido e num sentido de rotação conhecido. Na cinemática bidimensionais (a descrição de movimento planar), o eixo de rotação é perpendicular ao quadro de referência e pode ser representada por um ponto de rotação (ou centro), e o sentido de rotação está representado pelo sinal do ângulo (tipicamente, um sinal positivo significa sentido anti-horário). O deslocamento angular pode ser considerado como uma posição relativa. Ele é representado pelo ângulo orientado varrida pelo ponto supramencionado (ou vector), a partir de uma posição angular para outro.

Velocidade angular: A magnitude da velocidade angular 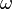$\ Omega$ é a taxa a que a posição angular $\ Theta$ mudanças com relação ao tempo t:

$\ Mathbf {\ omega} = \ frac {\ mathrm {d} \ theta} {\ mathrm {d} t}$

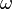Aceleração angular: A magnitude da aceleração angular $\ Alpha$ é a taxa à qual a velocidade angular $\ Omega$ mudanças com relação ao tempo t:

$\ Mathbf {\ alpha} = \ frac {\ mathrm {d} \ mathbf {\ omega}} {\ mathrm {d} t}$

As equações da cinemática de translação pode ser facilmente estendido para planar cinemática rotacional com trocas de variáveis simples:

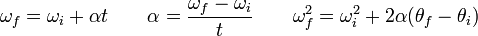
$\, \ \ Theta_f -! \ Theta_i = \ omega_i t + \ frac {1} {2} \ alpha t ^ 2 \ qquad \ theta_f - \ theta_i = \ frac {1} {2} (\ omega_f + \ omega_i) t$ $! \, \ \ Omega_f = \ omega_i + \ alpha t \ qquad \ alpha = \ frac {\ omega_f - \ omega_i} {t} \ qquad \ omega_f ^ 2 = \ omega_i ^ 2 + 2 \ alpha (\ theta_f - \ theta_i)$

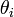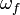Aqui $\, \! \ Theta_i$ e $\, \! \ Theta_f$ são, respectivamente, as posições angulares iniciais e finais, $\, \! \ Omega_i$ e $\, \! \ Omega_f$ são, respectivamente, as velocidades angulares iniciais e finais, e $\, \! \ Alpha$ é a aceleração angular constante. Embora a posição no espaço e velocidade no espaço são verdadeiros (ambos os vectores em termos das suas propriedades sob rotação), como é a velocidade angular, em si ângulo não é um verdadeiro vector.

Os sistemas de coordenadas

Em qualquer situação, as coordenadas mais úteis pode ser determinada pela restrições sobre o movimento, ou pela natureza geométrica da força que causa ou que afectam o movimento. Assim, para descrever o movimento de um grânulo constrangido a mover-se ao longo de um arco circular, o mais útil de coordenadas pode ser o seu ângulo sobre o aro. Da mesma forma, para descrever o movimento de uma partícula actuado por um força central, as coordenadas mais úteis podem ser coordenadas polares .

Coordenadas retangulares fixos

Neste sistema de coordenadas, vectores são expressos como uma adição de vectores em x, y, z e direcção a partir de uma origem não-rotativo. Normalmente i é um vector unitário na direcção x, j é um vector unitário na direcção y, e k é um vector unitário na direcção z.

O vector de posição, S (ou R), o vector de velocidade, v, e a aceleração do vetor, um são expressos em coordenadas rectangulares, da seguinte forma:

$\ S VEC = x \ vec i + y j vec \ + z \ vec k \, \!$

$\ Vec v = \ dot {s} = \ dot {x} \ vec {i} + \ dot {y} \ vec {j} + \ dot {z} \ vec {k} \, \!$

$\ Vec a = \ ddot {s} = \ ddot {x} \ vec {i} + \ ddot {y} \ vec {j} + \ ddot {z} \ vec {k} \, \!$

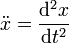
Nota: $\ Dot {x} = \ frac {\ mathrm {d}} {x \ mathrm {d} t}$ , $\ Ddot {x} = \ frac {\ mathrm {d} ^ 2x} {\ mathrm {d} t ^ 2}$

Coordenar três giro dimensional quadro

(A ser escrito)

Restrições cinemáticas

Um constrangimento cinemático é qualquer condição relativa propriedades de um sistema dinâmico, que devem ser verdadeiras em todos os momentos. Abaixo estão alguns exemplos comuns:

Rolando sem escorregar

Um objeto que rola contra um superfície sem escorregar obedece a condição de que a velocidade do seu centro de massa é igual ao produto vectorial da sua velocidade angular com um vector a partir do ponto de contacto com o centro de massa,:

$v_G (t) = \ omega \ times r_ {G / O} \, \!$

Para o caso de um objecto que não ponta ou virar, o que reduz a V = R ω.

Cabo inextensível

Este é o caso em que os corpos são ligados por uma corda que permanece em tensão e não pode alterar o comprimento. A restrição é de que a soma de todos os componentes do cabo, no entanto eles são definidos, é o comprimento total, e a derivada temporal desta soma é zero.

Retirado de " http://en.wikipedia.org/w/index.php?title=Kinematics&oldid=199418384 "

Home Page - YouTube Channel