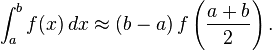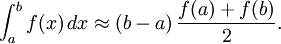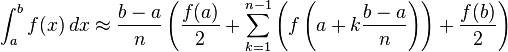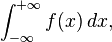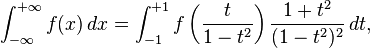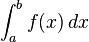Integração numérica
Informações de fundo
Esta seleção Wikipedia está offline disponível a partir de Crianças SOS, para distribuição no mundo em desenvolvimento. Visite o site da SOS Children at http://www.soschildren.org/


Em análise numérica, integração numérica constitui uma ampla família de algoritmos para calcular o valor numérico de uma definitiva integrante e, por extensão, o termo também é usado para descrever a solução numérica de equações diferenciais. Este artigo incide sobre o cálculo de integrais definidas. A quadratura numérica prazo (geralmente abreviado como quadratura) é mais ou menos um sinónimo de integração numérica, especialmente quando aplicado a integrais unidimensionais. Integração numérica ao longo de mais do que uma dimensão é por vezes descrito como cubagem, embora o significado de quadratura é entendida para maior integração dimensional, bem.
O problema básico considerado por integração numérica é calcular uma solução aproximada para uma integral definida:
Se f (x) é uma função bem-comportada suave, integrada ao longo de um pequeno número de dimensões e os limites da integração são delimitadas, existem muitos métodos de aproximar a integral com precisão arbitrária.
Razões para a integração numérica
Há várias razões para a realização de integração numérica. A f integrando (x) pode ser conhecida apenas em certos pontos, tal como obtido por amostragem . Alguns sistemas embarcados e outros aplicativos de computador pode precisar de integração numérica por este motivo.
Uma fórmula geral para o integrando pode ser conhecida, mas pode ser difícil ou impossível encontrar um primitiva, que é um função elementar. Um exemplo de tal um integrando é f (x) = exp (- x 2), a primitiva de que (a função de erro, vezes por constantes) não pode ser escrito em forma elementar.
Pode ser possível encontrar uma anti simbolicamente, mas pode ser mais fácil de calcular uma aproximação numérica do que para calcular a primitiva. Isto pode ser o caso se a primitiva é dada como uma série infinita ou produto, ou se a sua avaliação requer uma função especial que não está disponível.
Métodos para integrais unidimensionais
Métodos de integração numérica pode geralmente ser descrito como uma combinação de avaliações do integrando para obter uma aproximação para a integral. O integrando é avaliada em um conjunto finito de pontos chamados pontos de integração e uma soma ponderada desses valores é usada para aproximar a integral. Os pontos de integração e pesos dependem do método específico utilizado e a precisão requerida a partir da aproximação.
Uma parte importante da análise de qualquer método de integração numérica é estudar o comportamento do erro de aproximação como uma função do número de avaliações do integrando. Um método que produz um pequeno erro para um pequeno número de cálculos é geralmente considerada superior. A redução do número de avaliações do integrando reduz o número de operações aritméticas envolvido, e, por conseguinte, reduz o total de erro de arredondamento. Além disso, cada avaliação leva tempo, eo integrando pode ser arbitrariamente complicada.
Um tipo 'força bruta' de integração numérica pode ser feito, se o integrando for razoavelmente bem-comportado (ou seja, piecewise contínua e de variação limitada), através da avaliação do integrando com incrementos muito pequenos.
Regras de quadratura baseado em funções de interpolação
Uma grande classe de regras de quadratura pode ser derivada por meio da construção de interpolação funções que são de fácil integração. Normalmente essas funções de interpolação são polinômios .

O método mais simples deste tipo é permitir que a função de interpolação de ser uma função constante (um polinómio de grau zero), que passa através do ponto ((a + b) / 2, f ((a + b) / 2)). Esta é a chamada regra do ponto médio ou regra do retângulo.

A função de interpolação pode ser um função afim (um polinómio de grau 1), que passa pelos pontos (A, f (A)) e (b, f (b)). Isso é chamado de regra trapezoidal.

Para qualquer uma destas regras, nós podemos fazer uma aproximação mais precisa, quebrando-se o intervalo [a, b] em algum número n de subintervalos, computando uma aproximação para cada subintervalo, em seguida, adicionando-se todos os resultados. Isso é chamado de uma regra composta, regra estendida, ou regra iterado. Por exemplo, a regra trapezoidal compósito pode ser indicado como
onde os subintervalos tem a forma [k h, (k 1) h], com h = (b - a) / n e k = 0, 1, 2, ..., n-1.
Interpolação com polinômios avaliados em pontos espaçados em [a, b] produz o Fórmulas de Newton-Cotes, de que a regra do retângulo e do Estado trapezoidal são exemplos. Regra de Simpson, que se baseia em um polinómio de ordem 2, é também uma fórmula de Newton-Cotes.
Regras de quadratura com pontos espaçados têm a propriedade muito conveniente de aninhamento. A regra correspondente com cada intervalo subdividida inclui todos os pontos actuais, de modo que esses valores do integrando pode ser re-utilizado.
Se se permitir que os intervalos entre os pontos de interpolação para variar, encontramos outro grupo de fórmulas em quadratura, tal como o Fórmulas de quadratura de Gauss. Uma regra de quadratura de Gauss é tipicamente mais preciso do que uma regra de Newton-Cotes que requer o mesmo número de cálculos das funções, se o integrando é liso (ou seja, se for suficientemente diferenciável). Outros métodos de quadratura com intervalos variáveis incluem Clenshaw-Curtis quadratura (também chamado de quadratura Fejér) métodos, que fazem ninho.
Regras de quadratura de Gauss não fazer ninho, mas o relacionado Fórmulas de quadratura de Gauss-Kronrod fazer.
Algoritmos adaptativos
Se f (x) não tem muitos derivados em todos os pontos, ou se os derivados tornam-se grandes, então quadratura Gaussiana é muitas vezes insuficiente. Neste caso, um algoritmo semelhante ao seguinte terá melhor desempenho:
def calculate_definite_integral_of_f (f, initial_step_size): '' 'Este algoritmo calcula a integral definida de uma função 0-1, de forma adaptativa, escolhendo etapas menores perto de pontos problemáticos. '' 'X = 0,0 h = initial_step_size acumulador = 0,0, enquanto x <1.0: se x + h> 1,0: h = 1,0 - x = quad_this_step se error_too_big_in_quadrature_of_over_range (f, [x, x + h]): h = make_h_smaller (h ) else: acumulador + = quadrature_of_f_over_range (f, [x, x + h]) x + = h se error_too_small_in_quadrature_of_over_range (f, [x, x + h]): h = make_h_larger (h) # Evite perder tempo com pequenos passos. retorno acumulador
Alguns detalhes do algoritmo exigem uma reflexão cuidadosa. Para muitos casos, estimar o erro de quadratura através de um intervalo para uma função f (x) não é óbvia. Uma solução popular é usar dois diferentes regras de quadratura, e usar sua diferença como uma estimativa do erro de quadratura. O outro problema é decidir o que "muito grande" ou "muito pequeno" significam. Um critério local para "demasiado grande" é que o erro de quadratura não deve ser maior do que o t-h em que t, de um número real, é a tolerância que deseja definir para erro global. Então, novamente, se h já é pequena, pode não valer a pena para torná-lo ainda menor, mesmo que o erro de quadratura é aparentemente grande. Um critério global é que a soma de erros em todos os intervalos deve ser menor do que o t. Este tipo de análise de erro é normalmente chamado de "a posteriori", já que calculamos o erro depois de ter calculado a aproximação.
Heurística para quadratura adaptativa são discutidos por Forsythe et al. (Seção 5.4).
Métodos de extrapolação
A precisão de uma regra de quadratura do tipo de Newton-Cotes é geralmente uma função do número de pontos de avaliação. O resultado é geralmente mais preciso como o número de pontos de avaliação aumenta, ou, de forma equivalente, como a largura do tamanho do passo entre os pontos diminui. É natural que se pergunte o que o resultado seria se o tamanho do passo foram autorizados a aproximar-se de zero. Isso pode ser respondida por extrapolar o resultado de dois ou mais tamanhos de passo diferente de zero, usando métodos de aceleração da série, tais como Richardson extrapolação. A função pode ser uma extrapolação polinomial ou função racional. Extrapolação métodos são descritos em mais pormenor por Stoer e Bulirsch (Secção 3.4) e são implementadas em muitas das rotinas no Biblioteca QUADPACK.
Conservador (a priori) estimativa de erro
Seja f ter um primeiro derivado limitada sobre [a, b]. O teorema do valor médio para f, onde x <b, dá
para alguns Y X em [A, X] de acordo com x. Se nós integramos em x de um para b em ambos os lados e tomar os valores absolutos, obtemos
Podemos ainda aproximar a integral no lado da mão direita, trazendo o valor absoluto para o integrando, e substituindo o termo em f 'por um limite superior:
 (**)
(**)
(Ver supremum) Portanto, se aproximar a integral ∫ a b f (x) x d pela regra de quadratura (b -. a) f (a) nosso erro não é maior do que o lado direito de (**). Podemos converter isso em uma análise de erro para a soma de Riemann (*), dando um limite superior de
para o error prazo de que a aproximação particular. (Note que este é precisamente o erro foi calculado para o exemplo  .) Usando mais derivados, e por ajustes a quadratura, podemos fazer uma análise de erro semelhante usando uma série Taylor (usando uma soma parcial com prazo remanescente) para f. Esta análise erro dá um rigoroso limite superior sobre o erro, se os derivados de f estão disponíveis.
.) Usando mais derivados, e por ajustes a quadratura, podemos fazer uma análise de erro semelhante usando uma série Taylor (usando uma soma parcial com prazo remanescente) para f. Esta análise erro dá um rigoroso limite superior sobre o erro, se os derivados de f estão disponíveis.
Este método de integração pode ser combinado com aritmética intervalo para produzir provas de computador e cálculos verificados.
Integrais sobre intervalos infinitos
Intervalos infinitos
Uma maneira de calcular uma integral sobre intervalo infinito,
é transformá-lo em uma integral sobre um intervalo finito por qualquer uma das várias alterações possíveis de variáveis, como por exemplo:
A integral sobre intervalo finito pode então ser avaliado por métodos de integração comuns.
Intervalos de meia infinitos
Um integrante ao longo de um intervalo de meia-infinito pode igualmente ser transformado em um integrante ao longo de um intervalo finito por qualquer uma de várias alterações possíveis de variáveis, por exemplo:
Da mesma forma,
Integrais multidimensionais
As regras de quadratura discutidos até agora são todos concebidos para calcular integrais unidimensionais. Para calcular integrais em múltiplas dimensões, uma abordagem é a frase integral múltipla como repetidas integrais unidimensionais, apelando para Teorema de Fubini. Esta abordagem exige que as avaliações da função para crescer exponencialmente como o número de dimensões aumenta. Dois métodos são conhecidos para superar esta chamada maldição da dimensionalidade.
Monte Carlo
Métodos de Monte Carlo e métodos quase-Monte Carlo são fáceis de aplicar a integrais multidimensionais, e pode resultar em maior precisão para o mesmo número de avaliações da função de repetidas integrações usando métodos unidimensionais.
Uma grande classe de métodos de Monte Carlo úteis são os chamados Cadeia de Markov de Monte Carlo algoritmos, que inclui o Algoritmo de Metropolis-Hastings e Amostragem Gibbs.
Grades esparsos
Grades esparsas foram originalmente desenvolvidos por Smolyak para a quadratura de funções de alta dimensão. O método é sempre baseado em uma regra de quadratura unidimensional, mas realiza uma combinação mais sofisticado dos resultados univariadas.
Conexão com equações diferenciais
O problema de se avaliar a integral
pode ser reduzida para uma problema de valor inicial para uma equação diferencial ordinária . Se o integral acima é denotada por I (b), então a função que satisfaz
Métodos desenvolvidos para equações diferenciais ordinárias, tais como Métodos de Runge-Kutta, pode ser aplicada ao problema corrigidos e, assim, ser usado para calcular o integral. Por exemplo, a quarta ordem de Runge-Kutta padrão aplicado à equação diferencial produz a regra de Simpson de cima.
A equação diferencial I '(x) = f (x) tem uma forma especial: o lado direito contém apenas a variável dependente (aqui x) e não a variável independente (aqui I). Isto simplifica a teoria e algoritmos consideravelmente. O problema de avaliar integrais é, assim, melhor estudado em seu próprio direito.