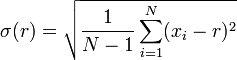Desvio padrão
Fundo para as escolas Wikipédia
Arranjar uma seleção Wikipedia para as escolas no mundo em desenvolvimento sem internet foi uma iniciativa da SOS Children. Veja http://www.soschildren.org/sponsor-a-child para saber mais sobre apadrinhamento de crianças.
Em probabilidade e estatística , o desvio padrão de uma distribuição de probabilidade , variável aleatória , ou população ou multiconjunto de valores é uma medida do espalhamento de seus valores. O desvio padrão é usualmente representada com a letra σ (letra minúscula Sigma). É definido como a raiz quadrada da variância .
Para compreender o desvio padrão, tenha em mente que a variância é a média das diferenças ao quadrado entre pontos de dados e da média. A variação é tabulados em unidades quadradas. O desvio padrão, sendo a raiz quadrada da quantidade que, por conseguinte, mede a propagação de dados em torno da média, medida nas mesmas unidades como os dados.
Dito de modo mais formal, o desvio padrão é o root mean square (RMS) desvio de valores a partir de sua média aritmética .
Por exemplo, na população {4, 8}, a média é de 6 e os desvios médio são {-2, 2}. Esses desvios quadrados são {4, 4} a média dos quais (a variância) é 4. Por conseguinte, o desvio padrão é de 2. Neste caso, 100% dos valores na população sao um desvio padrão da média.
O desvio padrão é a medida mais comum de dispersão estatística, medindo quão amplamente difundir os valores em um conjunto de dados são. Se muitos pontos de dados estão perto da média, o desvio padrão é pequeno; se muitos pontos de dados estão longe de ser a média, o desvio padrão, em seguida, é grande. Se todos os valores de dados são iguais, então o desvio padrão é zero.
Para população, o desvio padrão pode ser estimada por um desvio padrão modificado (s) de um amostra. As fórmulas são dadas abaixo.

 é uma medida do espalhamento dos valores da variável aleatória longe da sua média
é uma medida do espalhamento dos valores da variável aleatória longe da sua média 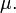
Definição e cálculo
Um exemplo simples
Suponha que nós desejamos para encontrar o desvio padrão do conjunto dos números 4 e 8.
Passo 1: encontrar a média aritmética (ou média) de 4 e 8,
Passo 2: encontrar o desvio de cada número a partir da média,
Passo 3: Quadrado cada um dos desvios (amplificando desvios maiores e fazendo valores negativos positivo),
Passo 4: soma dos quadrados obtidos (como um primeiro passo para a obtenção de uma média),
Passo 5: dividir a soma pelo número de valores, que aqui é 2 (dando uma média),
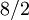 = 4.
= 4.
Passo 6: tirar a raiz quadrada não-negativa do quociente (conversão de unidades quadrados de volta para unidades regulares),
Assim, o desvio padrão é 2.
Desvio padrão de uma variável aleatória
O desvio padrão de uma variável aleatória X é definido como:
em que E (X) é a valor esperado de x, e Var (X) é a variância de X.
Nem todas as variáveis aleatórias têm um desvio padrão, uma vez que estes valores esperados não precisa existir. Por exemplo, o desvio padrão de uma variável aleatória, que segue uma Distribuição de Cauchy é indefinido, porque seu E (X) é indefinido.
Se a variável aleatória X assume os valores 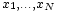 (Que são números reais ), com igual probabilidade, em seguida, o seu desvio padrão pode ser calculado como se segue. Em primeiro lugar, a média de X,
(Que são números reais ), com igual probabilidade, em seguida, o seu desvio padrão pode ser calculado como se segue. Em primeiro lugar, a média de X,  , É definido como um somatório:
, É definido como um somatório:
onde N é o número de amostras tomadas. Em seguida, o desvio padrão para simplifica
Em outras palavras, o desvio padrão de uma variável aleatória X discreta uniforme pode ser calculado como se segue:
- Para cada valor
 calcular a diferença
calcular a diferença  entre x i e o valor médio
entre x i e o valor médio  .
. - Calcular os quadrados dessas diferenças.
- Encontre a média das diferenças ao quadrado. Esta quantidade é a variância σ 2.
- Tirar a raiz quadrada da variância.
A expressão acima também pode ser substituído com
Igualdade destas duas expressões pode ser demonstrado por um pouco de álgebra:
Desvio padrão de uma variável aleatória contínua
Distribuições contínuas geralmente dar uma fórmula para o cálculo do desvio padrão como uma função dos parâmetros da distribuição. Em, o desvio-padrão geral de uma variável aleatória contínua X com função de densidade de probabilidade p (x) é
Onde
Exemplo
Vamos mostrar como calcular o desvio padrão de uma população. Nosso exemplo usará as idades de quatro filhos: {5, 6, 8, 9}.
Passo 1. Calcule a média média ,  :
:
Temos N = 4 porque existem quatro pontos de dados:
 Substituto N = 4
Substituto N = 4
Passo 2. Calcular o desvio padrão,  . (Uma vez que os quatro valores representam toda a população, não usamos a fórmula para o desvio padrão estimado neste caso):
. (Uma vez que os quatro valores representam toda a população, não usamos a fórmula para o desvio padrão estimado neste caso):
 Substituto
Substituto  = 7 e n = 4
= 7 e n = 4
Assim, o desvio padrão das idades dos quatro filhos é a raiz quadrada de 2,5, ou aproximadamente 1.58.
Se isso fosse definida uma amostra extraída de uma população maior de crianças, ea questão em apreço era uma estimativa do desvio-padrão da população, convenção iria substituir o denominador N (ou 4) na etapa 2 aqui com N-1 (ou 3 ).
Interpretação e aplicação
Um grande desvio padrão indica que os pontos de dados estão longe de ser a média e um desvio padrão pequeno indica que eles estão agrupados estreitamente em torno da média.
Por exemplo, cada um dos três conjuntos de dados {0, 0, 14, 14}, {0, 6, 8, 14} e {6, 6, 8, 8} tem uma média de 7. Os desvios-padrão são 7, 5, e 1, respectivamente. O terceiro conjunto tem um desvio padrão muito menor do que os outros dois porque seus valores são todos perto de 7. Em um sentido amplo, o desvio-padrão nos diz quão longe a partir da média dos pontos de dados tendem a ser. Ele terá as mesmas unidades como os dados aponta-se. Se, por exemplo, o conjunto de dados {0, 6, 8, 14} representa as idades de quatro irmãos em anos, o desvio padrão é de 5 anos.
Como outro exemplo, o conjunto de dados {1000, 1006, 1008, 1014} pode representar as distâncias percorridas por quatro atletas, medido em metros. Ele tem uma média de 1.007 metros, e um desvio padrão de 5 metros.
Desvio padrão pode servir como uma medida de incerteza. Na ciência física, por exemplo, o desvio padrão relatado de um grupo de repetidas as medições deve dar a precisão dessas medições. Ao decidir se as medições de acordo com uma previsão teórica, o desvio padrão das referidas medições é de importância crucial: se a média das medições é muito longe da predição (com a distância medida em desvios-padrão), então a teoria a ser testada provavelmente precisa de ser revista. Isso faz sentido, uma vez que estão fora da faixa de valores que podem ser razoavelmente esperados para ocorrer se a previsão fosse correta eo desvio padrão adequadamente quantificadas. Ver intervalo de previsão.
Exemplos da vida real
O valor prático de compreender o desvio padrão de um conjunto de valores é de apreciar a quantidade de variação não é do "média" (média).
Tempo
Como um exemplo simples, considere as temperaturas médias para as cidades. Enquanto duas cidades podem ter cada um uma temperatura média de 60 ° F, é útil para entender que o intervalo para cidades próximas da costa é menor do que para cidades do interior, que esclarece que, enquanto a média é semelhante, a chance de variação é maior do que no interior, perto da costa.
Assim, uma média de 60 ocorre para uma cidade com máxima de 80 ° C e mínima de 40 ° C, e também ocorre para outra cidade com picos de 65 e baixos de 55. O desvio-padrão nos permite reconhecer que a média para o cidade com a maior variação, e, portanto, um desvio padrão mais elevado, não vai oferecer como uma previsão confiável de temperatura como a cidade com a menor variação e desvio padrão mais baixo.
Esportes
Outra maneira de vê-lo é considerar as equipes de esportes. Em qualquer conjunto de categorias, haverá equipes que avaliam altamente em algumas coisas e mal em outros. As possibilidades são, as equipes que levam na classificação não mostrará uma disparidade tão grande, mas vai ser muito bom na maioria das categorias. Quanto mais baixo o desvio padrão de suas classificações em cada categoria, a mais equilibrada e coerente que possa ser. Assim, uma equipe que é sempre ruim na maioria das categorias terá um desvio padrão baixo. Uma equipe que é sempre boa na maioria das categorias também terão um desvio de baixo padrão. Uma equipe com um desvio padrão elevado pode ser o tipo de equipa que marcar um monte (ofensa forte), mas também admite um lote (defesa fraca), ou, vice-versa, que pode ter uma ofensa pobre, mas compensa por ser difícil de marcar em -teams com um desvio padrão mais elevado será mais imprevisível.
Tentar prever que as equipes, em um determinado dia, vai ganhar, pode incluir a olhar para os desvios-padrão dos vários equipe "estatísticas" classificações, nas quais anomalias podem combinar os pontos fortes contra fracos para tentar entender quais os fatores que podem prevalecer como indicadores mais fortes de eventuais resultados de pontuação.
Nas corridas, um motorista é cronometrado em voltas sucessivas. Um motorista com um baixo desvio padrão de tempos de volta é mais consistente do que um motorista com um desvio padrão mais elevado. Esta informação pode ser usada para ajudar a compreender onde as oportunidades pode ser encontrada para reduzir os tempos de volta.
Finanças
Em finanças, o desvio padrão é uma representação do risco associado a um determinado segurança (ações, títulos, propriedade, etc.), ou o risco de uma carteira de valores mobiliários. O risco é um fator importante na determinação de como gerenciar com eficiência uma carteira de investimentos, pois determina a variação no retorno sobre o ativo e / ou carteira e dá aos investidores uma base matemática para decisões de investimento. O conceito geral de risco é que à medida que aumenta, o retorno esperado sobre o ativo irá aumentar como resultado do prémio de risco ganhou - em outras palavras, os investidores devem esperar um maior retorno sobre o investimento, quando disse que o investimento traz um nível mais elevado de risco .
Por exemplo, você tem uma escolha entre duas ações: da A retorna historicamente 5%, com um desvio padrão de 10%, enquanto da B retorna 6% e leva um desvio padrão de 20%. Com base no risco e retorno, o investidor pode decidir que da A é a melhor escolha, porque ponto percentual adicional de da B de retorno gerado (mais 20% em termos de dólares) não vale o dobro do grau de risco associado ao da A . da B é provável que ficam aquém do investimento inicial mais frequentemente do que da A nas mesmas circunstâncias, e irá retornar apenas um ponto percentual a mais, em média. Neste exemplo, da A tem o potencial para ganhar 10% a mais do que o retorno esperado, mas tem a mesma probabilidade de ganhar 10% menos do que o retorno esperado.
Calculando a média de retorno (ou média aritmética) de uma garantia sobre um determinado número de períodos irá gerar um retorno esperado sobre o ativo. Para cada período, subtraindo o retorno esperado a partir dos resultados de retorno reais na variância. Quadrada da variância em cada período para encontrar o efeito do resultado sobre o risco total do ativo. Quanto maior for a variância de um período, o maior risco a segurança carrega. Tomando a média dos desvios quadrados resulta na medição de unidades globais de risco associados ao activo. Encontrar a raiz quadrada da variância este irá resultar no desvio padrão da ferramenta de investimento em questão. Use esta medida, combinada com o retorno médio sobre a segurança, como base para a comparação de valores mobiliários.
Interpretação geométrica
Para ganhar alguns insights geométricas, vamos começar com uma população de três valores, x 1, x 2, x 3. Isto define um ponto P = (x 1, x 2, x 3) em R3. Considere a linha G = {(R, R, R): r em R}. Este é o "diagonal principal" que passa pela origem. Se os três valores indicados foram todos iguais, então o desvio padrão seria zero e P que se encontram em L. Portanto, não é razoável supor que o desvio padrão está relacionada com a distância de P para L. E isso é realmente o caso. Movendo ortogonal de P para a linha L, uma atinge o ponto:
cujas coordenadas são a média dos valores que começou com. Um pouco de álgebra mostra que a distância entre P e R (que é a mesma que a distância entre P e a linha L) é dada por σ√ 3. Uma fórmula análoga (com 3 substituído por N) também é válido para uma população de N valores; então, temos que trabalhar em R N.
Regras para dados distribuídos normalmente

Na prática, um muitas vezes assume que os dados são de um aproximadamente normalmente distribuído população. Este é frequentemente justificada pela clássica teorema do limite central, que diz que somas de muitos, variáveis aleatórias independentes e identicamente distribuídas tendem para a distribuição normal como um limite. Se pressuposto de que se justifica, em seguida, cerca de 68% dos valores estão dentro de um desvio padrão da média, cerca de 95% dos valores estão dentro de dois desvios padrão e cerca de 99,7% se encontram dentro de três desvios padrão. Isto é conhecido como o 68-95-99.7 regra ou a regra empírica.
O intervalos de confiança são como se segue:
| σ | 68,26894921371% |
| 2σ | 95,44997361036% |
| 3σ | 99,73002039367% |
| 4σ | 99,99366575163% |
| 5σ | 99,99994266969% |
| 6σ | 99,99999980268% |
| 7σ | 99,99999999974% |
Para as distribuições normais, os dois pontos da curva, que são um desvio padrão da média são também o pontos de inflexão.
Desigualdade de Chebyshev
Desigualdade de Chebyshov prova que em qualquer conjunto de dados, quase todos os valores serão mais perto do valor da média, em que o significado de "perto" é especificado pelo desvio padrão. Desigualdade de Chebyshev implica que, para (quase) todas as distribuições aleatórias, e não apenas os normais, temos o seguinte limites mais fracos:
- Pelo menos 50% dos valores estão dentro √2 desvios padrão da média.
- Pelo menos 75% dos valores estão dentro de dois desvios padrão da média.
- Pelo menos 89% dos valores estão dentro de 3 desvios padrão da média.
- Pelo menos 94% dos valores estão dentro de quatro desvios padrão da média.
- Pelo menos 96% dos valores estão dentro de 5 desvios padrão da média.
- Pelo menos 97% dos valores estão dentro de seis desvios padrão da média.
- Pelo menos 98% dos valores estão dentro de sete desvios padrão da média.
E, em geral:
- Pelo menos (1-1 / 2 K) x 100% dos valores estão dentro k desvios padrão da média.
Relação entre o desvio padrão ea média
A média eo desvio padrão de um conjunto de dados geralmente são relatados juntos. Em certo sentido, o desvio padrão é uma medida "natural" de dispersão estatística, quando o centro de dados é medido em relação à média. Isto é porque o desvio padrão da média é menor do que de qualquer outro ponto. A declaração precisa é o seguinte: suponha que x 1, ..., x n são números reais e definir a função:
Usando o cálculo , ou simplesmente pela completar o quadrado, é possível mostrar que σ (R) tem um mínimo único na média:
(Isso também pode ser feito com álgebra bastante simples sozinho, uma vez que σ 2 (r) é equiparado a um polinômio quadrático).
O coeficiente de variação de uma amostra é o quociente entre o desvio padrão para a média. É um número adimensional que pode ser utilizado para comparar a quantidade de variância entre populações com diferentes meios.
Métodos de cálculo rápidas
Um pouco mais rápido (significativamente para a execução de desvio padrão) maneira de calcular o desvio padrão da população é dada pela seguinte fórmula (embora considerações devem ser tomadas medidas para erro de arredondamento, estouro aritmético, e underflow condições aritméticas):
ou
onde as somas de energia s 0, S 1, S 2 são definidas pela
Da mesma forma para o desvio padrão da amostra:
Ou seja executado somas:


















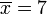

![\ Sigma = \ sqrt {\ frac {1} {4} \ left [(x_1 - 7) ^ 2 + (x_2 - 7) ^ 2 + (x_3 - 7) ^ 2 + (x_4 - 7) ^ 2 \ right ]}](../../images/135/13580.png)
![\ Sigma = \ sqrt {\ frac {1} {4} \ left [(5-7) ^ 2 + (6-7) ^ 2 + (8-7) ^ 2 + (9-7) ^ 2 \ right ]}](../../images/135/13581.png)