
Interpolación
Acerca de este escuelas selección Wikipedia
SOS Children ha intentado que el contenido de Wikipedia más accesible por esta selección escuelas. Visite el sitio web de Aldeas Infantiles SOS en http://www.soschildren.org/
En la matemática subcampo de análisis numérico, la interpolación es un método de construcción de nuevos puntos de datos dentro de la gama de una conjunto discreto de puntos de datos conocidos.
En la ingeniería y la ciencia a menudo se tiene una serie de puntos de datos, tal como se obtiene por muestreo o experimento, y trata de construir una función que se ajusta estrechamente esos puntos de datos. Se llama curva de ajuste o el análisis de regresión . La interpolación es un caso específico de ajuste de curvas, en el que la función debe ir exactamente a través de los puntos de datos.
Un problema diferente que está estrechamente relacionado con la interpolación es la aproximación de una función complicada por una función simple. Supongamos que conocemos la función, pero es demasiado complejo para evaluar de manera eficiente. Entonces podríamos elegir un pocos puntos de datos conocidos de la función complicada, creando un Tabla de búsqueda, y tratar de interpolar los puntos de datos para construir una función simple. Por supuesto, cuando se utiliza la función simple para calcular los nuevos puntos de datos que normalmente no recibimos el mismo resultado que cuando se utiliza la función original, pero dependiendo del dominio del problema y el método de interpolación usan la ganancia en simplicidad podría compensar el error.
Cabe mencionar que hay otro tipo muy diferente de la interpolación en las matemáticas, a saber, el " interpolación de los operadores ". Los resultados clásicas sobre la interpolación de los operadores son los Riesz-Thorin teorema y la Teorema de Marcinkiewicz. También hay muchos otros resultados posteriores.
Definición
De entre significado y entre polos, los puntos o nodos. Por tanto, cualquier medio para calcular un nuevo punto entre dos puntos de datos existentes es la interpolación.
Hay muchos métodos para hacer esto, muchos de los cuales implican algún tipo de ajuste de la función a los datos y la evaluación de que la función en el punto deseado. Esto no excluye otros medios tales como los métodos estadísticos de cálculo de los datos interpolados.
La forma más simple de interpolación es tomar la media aritmética de 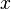 y
y  de dos puntos adyacentes para encontrar el punto medio. Esto le dará el mismo resultado que la interpolación lineal evaluado en el punto medio.
de dos puntos adyacentes para encontrar el punto medio. Esto le dará el mismo resultado que la interpolación lineal evaluado en el punto medio.
Dada una secuencia de n números distintos x k llamados nodos y para cada x k un segundo número y k, que estamos buscando una función f de manera que
Un par x k, k y se llama un punto de datos y f se llama un interpolador para los puntos de datos.
Cuando el número y k vienen dados por una función conocida f, a veces nos escribimos f k.
Ejemplo
Por ejemplo, supongamos que tenemos una tabla como ésta, que da algunos valores de una función desconocida f.
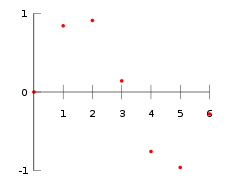
| x | f (x) | ||||
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 1 | 0 | . | 8415 | ||
| 2 | 0 | . | 9093 | ||
| 3 | 0 | . | 1411 | ||
| 4 | -0 | . | 7568 | ||
| 5 | -0 | . | 9589 | ||
| 6 | -0 | . | 2794 | ||
La interpolación proporciona un medio de estimación de la función en puntos intermedios, tales como x = 2,5.
Hay muchos métodos de interpolación diferentes, algunos de los cuales se describen a continuación. Algunas de las preocupaciones a tener en cuenta al elegir un apropiado algoritmo son: ¿Qué tan exacto es el método? ¿Qué tan caro es? Cómo suave es el interpolante? ¿Cuántos datos se necesitan puntos?
Interpolación constante a trozos

El método de interpolación más sencilla es la de localizar el valor de datos más cercano, y asignar el mismo valor. En una dimensión, rara vez hay buenas razones para elegir este uno sobre la interpolación lineal, que es casi tan barato, pero en dimensiones más altas, en interpolación multivariado, esto puede ser una opción favorable por su velocidad y simplicidad.
Interpolación linear

Uno de los métodos más simples es interpolación lineal (a veces conocido como lerp). Considere el ejemplo anterior de la determinación de f (2,5). Desde 2.5 está a medio camino entre 2 y 3, es razonable tomar f (2.5) a medio camino entre f (2) = 0.9093 y f (3) = 0,1411, que produce 0,5252.
Generalmente, la interpolación lineal tiene dos puntos de datos, por ejemplo (x a, y a) y (b x, y b), y el interpolador está dada por:
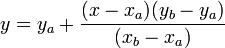 en el punto (x, y).
en el punto (x, y).
La interpolación lineal es rápida y fácil, pero no es muy preciso. Otra desventaja es que el interpolador no es diferenciable en el punto x k.
La siguiente estimación del error de interpolación lineal muestra que no es muy precisa. Denotar la función que queremos interpolar por g, y supongamos que x está entre x a y x b y que g es dos veces continuamente diferenciable. A continuación, el error de interpolación lineal es
En palabras, el error es proporcional al cuadrado de la distancia entre los puntos de datos. El error de algunos otros métodos, incluyendo la interpolación polinómica y la interpolación spline (descrito a continuación), es proporcional a mayores potencias de la distancia entre los puntos de datos. Estos métodos también producen interpolantes más suaves.
La interpolación polinómica

Interpolación polinómica es una generalización de la interpolación lineal. Tenga en cuenta que el interpolador lineal es una función lineal. Ahora Reemplazamos este interpolante por un polinomio de mayor grado.
Consideremos de nuevo el problema dado anteriormente. La siguiente sexto grado del polinomio pasa por todos los siete puntos:
Sustituyendo x = 2.5, encontramos que f (2,5) = 0.5965.
En general, si tenemos n puntos de datos, no es exactamente un polinomio de grado a lo sumo n -1 pasar por todos los puntos de datos. El error de interpolación es proporcional a la distancia entre los puntos de datos a la potencia n. Además, el interpolador es un polinomio y por lo tanto infinitamente diferenciable. Así, vemos que la interpolación polinómica resuelve todos los problemas de la interpolación lineal.
Sin embargo, la interpolación polinómica también tiene algunas desventajas. Cálculo del polinomio de interpolación es relativamente muy computacionalmente caro (ver complejidad computacional). Además, la interpolación polinómica puede no ser tan exacto después de todo, sobre todo en los puntos finales (véase Fenómeno de Runge). Estas desventajas se pueden evitar mediante el uso de la interpolación spline.
Interpolación Spline

Recuerde que la interpolación lineal utiliza una función lineal para cada uno de los intervalos [x k, x k + 1]. Interpolación spline utiliza polinomios de bajo grado en cada uno de los intervalos, y elige las piezas polinómicas de manera que encajan sin problemas juntos. La función resultante se llama una spline.
Por ejemplo, la spline cúbico natural es trozos cúbicos y dos veces continuamente diferenciable. Además, su segunda derivada es cero en los puntos finales. El spline cúbico natural de interpolación de los puntos en la tabla de arriba está dada por
En este caso obtenemos f (2,5) = 0,597262.
Al igual que la interpolación polinómica, interpolación spline incurre en un error menor que la interpolación lineal y el interpolador es más suave. Sin embargo, el interpolador es más fácil de evaluar que los polinomios de alto grado se utilizan en la interpolación polinómica. También no sufre de Fenómeno de Runge.
Otras formas de interpolación
Otras formas de interpolación se pueden construir por recoger una clase diferente de interpolantes. Por ejemplo, interpolación racional es la interpolación por funciones racionales, y interpolación trigonométrica es interpolación por polinomios trigonométricos. La transformada discreta de Fourier es un caso especial de la interpolación trigonométrica. Otra posibilidad es utilizar wavelets.
La Fórmula de interpolación Whittaker-Shannon se puede utilizar si el número de puntos de datos es infinito.
Interpolación multivariable es la interpolación de las funciones de más de una variable. Los métodos incluyen interpolación bilineal y interpolación bicúbica en dos dimensiones, y interpolación trilineal en tres dimensiones.
A veces, sabemos no sólo el valor de la función que queremos interpolar, en algunos puntos, pero también su derivado. Esto lleva a Problemas de interpolación de Hermite.
Conceptos relacionados
El término extrapolación se utiliza si queremos encontrar puntos de datos fuera de la gama de puntos de datos conocidos.
En curva de problemas de ajuste, la restricción de que el interpolador tiene que ir exactamente a través de los puntos de datos es relajado. Sólo se requiere para acercarse a los puntos de datos tan estrechamente como sea posible. Esto requiere la parametrización de los interpolantes potenciales y tener alguna manera de medir el error. En el caso más simple esto conduce a mínimos cuadrados aproximación.
Estudios de teoría de la aproximación de cómo encontrar la mejor aproximación a una función dada por otra función de alguna clase predeterminado, y lo bien que esta aproximación es. Esto produce claramente un salto de lo bien que el interpolador puede aproximar la función desconocida.
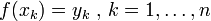
![| F (x) -g (x) | \ le C (X_b-x_a) ^ 2 \ quad \ mbox {} donde \ quad C = \ frac18 \ max_ {y \ in [x_a, X_b]} | g '' (y) |.](../../images/71/7171.png)

![f (x) = \ left \ {\ begin {matriz} -0,1522 x ^ 3 + 0,9937 x, y \ mbox {si} x \ in [0,1], \\ -0.01258 x ^ 3 a 0,4189 x ^ 2 + 1,4126 x - 0,1396, y \ mbox {si} x \ in [1,2], \\ 0,1403 x ^ 3 a 1,3359 x ^ 2 + x 3,2467 - 1,3623, y \ mbox {si} x \ in [2, 3], \\ 0,1579 x ^ 3 a 1,4945 x ^ 2 + x 3.7225 - 1.8381, y \ mbox {si} x \ in [3,4], \\ 0,05375 x ^ 3 -0,2450 x ^ 2 a 1,2756 x + 4,8259, y \ mbox {si} x \ in [4,5], \\ -0,1871 x ^ 3 + 3,3673 x ^ 2-19,3370 x + 34.9282, & \ mbox {si} x \ in [5,6]. \\ \ End {matriz} \ right.](../../images/71/7182.png)
