
Teoria quântica de campos
Fundo para as escolas Wikipédia
Crianças SOS feita esta seleção Wikipedia ao lado de outras escolas recursos . Visite o site da SOS Children at http://www.soschildren.org/
| Teoria quântica de campos |
|---|
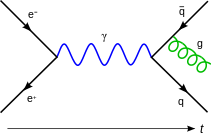 Feynman diagrama |
| História |
Fundo
|
Simetrias
|
Ferramentas
|
Equações
|
|
Teorias incompletas
|
Os cientistas
|
Teoria quântica de campos (QFT) é uma estrutura teórica para a construção mecânica quântica modelos de campo-como sistemas ou, equivalente, de sistemas de muitos corpos. É amplamente utilizado em física de partículas e física da matéria condensada . A maioria das teorias em física de partículas moderna, incluindo o modelo padrão das partículas elementares e suas interações, são formuladas como relativistas teorias quânticas de campo. Em física da matéria condensada, teorias de campos são usados em muitas circunstâncias, especialmente aqueles em que o número de partículas é deixada a flutuar, por exemplo, na Teoria BCS de supercondutividade .
História
Teoria quântica de campos originou no 1920 do problema de criar uma teoria mecânica quântica da campo eletromagnético. Em 1926 , Max Born, Pascual Jordão, e Werner Heisenberg construído tal teoria, expressando o campo de interno graus de liberdade como um conjunto infinito de osciladores harmônicos e empregando o procedimento usual para a quantificação desses osciladores ( quantização canônica). Esta teoria do princípio de que não há cargas elétricas ou correntes estavam presentes e hoje seria chamado de teoria do campo livre. A primeira teoria razoavelmente completo de eletrodinâmica quântica, que incluíam tanto o campo eletromagnético e eletricamente carregadas matéria (especificamente, elétrons ) como objetos de mecânica quântica, foi criado por Paul Dirac em 1927 . Esta teoria quântica de campos pode ser usada para modelar processos importantes, tais como a emissão de um fóton por um elétron caindo em um estado quantum de energia mais baixa, um processo em que o número de partículas de alterações - um átomo no estado inicial torna-se mais de um átomo de um fotão no estado final. Agora Entende-se que a capacidade de descrever tais processos é uma das características mais importantes da teoria quântica de campos.
Era evidente desde o início que um tratamento adequado quântica do campo eletromagnético tinha de alguma forma incorporar de Einstein da relatividade teoria, que tinha afinal crescido fora do estudo da eletromagnetismo clássico. Esta necessidade de reunir relatividade ea mecânica quântica foi a segunda maior motivação no desenvolvimento da teoria quântica de campos. Pascual Jordan e Wolfgang Pauli mostrou em 1928 que os campos quânticos poderiam ser feitas para se comportar da maneira prevista pela relatividade especial durante transformações de coordenadas (especificamente, eles mostraram que o campo comutadores foram Lorentz invariante), e em 1933 Niels Bohr e Leon Rosenfeld mostrou que este resultado pode ser interpretado como uma limitação sobre a capacidade de medir os campos em separações espaço-like, exatamente como exigido pela relatividade. Um novo impulso para a teoria quântica de campos veio com a descoberta do Equação de Dirac, uma equação de uma única partícula obedecendo tanto a relatividade ea mecânica quântica, quando foi mostrado que várias de suas propriedades indesejáveis (tais como estados de energia negativa) poderia ser eliminada, reformulando a equação de Dirac como uma teoria quântica de campos. Este trabalho foi realizado por Wendell Furry, Robert Oppenheimer , Vladimir Fock, e outros.
O terceiro segmento no desenvolvimento da teoria quântica de campos foi a necessidade de lidar com as estatísticas dos sistemas de muitas partículas de forma consistente e com facilidade. Em 1927 , Jordan tentou estender a quantização canônica de campos para as funções de onda de muitos corpos de partículas idênticas, um processo que às vezes é chamado segunda quantização. Em 1928 , a Jordânia e Eugene Wigner descobriu que o campo quântico descrever elétrons, ou outro férmions, teve de ser expandida usando anti-pendulares operadores de criação e aniquilação devido à Princípio de exclusão de Pauli. Esta discussão do desenvolvimento foi incorporada teoria de muitos corpos, e fortemente influenciada física da matéria condensada e física nuclear .
Apesar de seus primeiros sucessos, a teoria quântica de campos foi atormentado por várias dificuldades teóricas graves. Muitas quantidades físicas aparentemente inócuos-, tais como a mudança de energia de estados eletrônicos devido à presença do campo eletromagnético, deu infinito - um resultado absurdo - quando calculado usando a teoria quântica de campos. Este "problema de divergência" foi resolvido durante a 1940 por Bethe, Tomonaga, Schwinger, Feynman , e Dyson, através do procedimento conhecido como renormalização . Esta fase de desenvolvimento culminou com a construção da moderna teoria da eletrodinâmica quântica (QED). Começando no 1950 com o trabalho de Yang e Mills, QED foi generalizado a uma classe de teorias quânticas de campos conhecidos como teorias de gauge. O 1960 e 1970 viu a formulação de uma teoria de calibre agora conhecido como o Modelo Padrão da física de partículas , que descreve todas as partículas elementares conhecidas e as interações entre eles. A parte fraca interação do modelo padrão foi formulada por Sheldon Glashow, com a Mecanismo de Higgs adicionado por Steven Weinberg e Abdus Salam. A teoria demonstrou ser consistente por Gerardus 't Hooft e Martinus Veltman.
Também durante o 1970, desenvolvimentos paralelos no estudo de transições de fase em física da matéria condensada liderada Leo Kadanoff, Michael Fisher e Kenneth Wilson (que se estende de trabalho Ernst Stueckelberg, Andre Peterman, Murray Gell-Mann e Francis Low) a um conjunto de idéias e métodos conhecido como grupo de renormalização. Ao fornecer uma melhor compreensão física do procedimento renormalization inventado no 1940, o grupo de renormalização provocou o que tem sido chamado de "grande síntese" da física teórica, unindo as técnicas teóricas de campo quântico usados na física de partículas e física da matéria condensada em um referencial teórico único.
O estudo da teoria quântica de campos está vivo e florescente, como são aplicações deste método para muitos problemas físicos. Ele continua sendo uma das áreas mais vitais do física teórica hoje, fornecendo uma linguagem comum para muitos ramos da física .
Princípios da teoria quântica de campos
Campos clássicos e campos quânticos
A mecânica quântica , na sua formulação mais geral, é uma teoria abstrata de operadores (observáveis) atuando em um espaço abstrato do Estado ( Espaço de Hilbert), onde os observáveis representam quantidades fisicamente observáveis eo espaço estado representa os possíveis estados do sistema em estudo. Além disso, cada observável corresponde, em sentido técnico, com a idéia clássica de um grau de liberdade. Por exemplo, os observáveis fundamentais associados com o movimento de uma única partícula da mecânica quântica são os operadores a posição eo momento  e
e  . Mecânica quântica comuns lida com sistemas como este, que possuem um pequeno conjunto de graus de liberdade.
. Mecânica quântica comuns lida com sistemas como este, que possuem um pequeno conjunto de graus de liberdade.
(É importante notar, neste ponto, que este artigo não usa a palavra " partícula ", no contexto de dualidade onda-partícula. Em teoria quântica de campos, "partícula" é um termo genérico para qualquer entidade mecânica quântica discreto, tal como um elétron, que pode se comportar como partículas clássicas ou ondas clássicas sob diferentes condições experimentais.)
Um campo quântica é um sistema mecânico quântico contendo um grande, e possivelmente infinito , o número de graus de liberdade. Isto não é tão exótico numa situação como se poderia pensar. A campo clássico contém um conjunto de graus de liberdade em cada ponto do espaço; por exemplo, a clássica campo eletromagnético define dois vectores - o campo elétrico eo campo magnético - que podem, em princípio, assumir valores distintos para cada posição  . Quando o campo como um todo é considerada como um sistema de mecânica quântica, as suas observáveis formar um infinito (na verdade incontável) set, porque
. Quando o campo como um todo é considerada como um sistema de mecânica quântica, as suas observáveis formar um infinito (na verdade incontável) set, porque  é contínua.
é contínua.
Além disso, os graus de liberdade em um campo quântico são dispostos em conjuntos de "repetidas". Por exemplo, os graus de liberdade em um campo eletromagnético podem ser agrupados de acordo com a posição  , Com exactamente dois vectores para cada
, Com exactamente dois vectores para cada  . Note que
. Note que  é um número comum, que "índices" os observáveis; não deve ser confundido com o operador posição
é um número comum, que "índices" os observáveis; não deve ser confundido com o operador posição  encontrado na mecânica quântica comum, que é um observável. (Assim, a mecânica quântica comum é muitas vezes referida como "teoria do campo quântico de dimensão zero", porque contém apenas um único conjunto de observáveis.) Também é importante notar que não há nada de especial sobre
encontrado na mecânica quântica comum, que é um observável. (Assim, a mecânica quântica comum é muitas vezes referida como "teoria do campo quântico de dimensão zero", porque contém apenas um único conjunto de observáveis.) Também é importante notar que não há nada de especial sobre  porque, como se vê, há geralmente mais de uma maneira de indexar os graus de liberdade no campo.
porque, como se vê, há geralmente mais de uma maneira de indexar os graus de liberdade no campo.
Nas seções seguintes, vamos mostrar como essas idéias podem ser usados para construir uma teoria da mecânica quântica com as propriedades desejadas. Vamos começar por discutir de partícula única mecânica quântica ea teoria da mecânica quântica associada de muitas partículas. Então, por encontrar uma maneira de indexar os graus de liberdade no problema de muitas partículas, vamos construir um campo quântico e estudar as suas implicações.
Single-partículas e mecânica quântica de muitas partículas
Na mecânica quântica comuns, o tempo-dependente Equação de Schrödinger descreve o movimento de uma única partícula não relativística é
onde  é o de partícula de massa ,
é o de partícula de massa ,  é a aplicada potencial, e
é a aplicada potencial, e 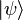 indica o estado quântico (estamos usando notação bra-ket).
indica o estado quântico (estamos usando notação bra-ket).
Queremos considerar como esse problema generaliza a  partículas. Há duas motivações para estudar o problema de muitas partículas. A primeira é uma necessidade clara na física da matéria condensada , em que tipicamente o número de partículas é na ordem de número de Avogadro (6.0221415 x 10 23). A segunda motivação para o problema de muitas partículas surge da física de partículas eo desejo de incorporar os efeitos da relatividade especial . Se alguém tenta incluir o relativista a energia restante na equação acima, o resultado é tanto a Equação de Klein-Gordon ou o Equação de Dirac. No entanto, essas equações têm muitas qualidades insatisfatórios; por exemplo, eles possuem energia valores próprios , que se estendem para -∞, de modo que parece haver nenhuma definição de um fácil estado fundamental. Acontece que essas inconsistências surgem de descurar a possibilidade de criar dinamicamente ou destruir partículas, o que é um aspecto crucial da relatividade. Einstein famoso relação massa-energia prevê que as partículas suficientemente maciças pode decair em várias partículas mais leves, e suficientemente partículas energéticas podem se combinar para formar partículas maciças. Por exemplo, um elétron e um pósitrons pode aniquilar uns aos outros para criar fótons . Assim, uma teoria quântica relativista consistente deve ser formulada como uma teoria de muitas partículas.
partículas. Há duas motivações para estudar o problema de muitas partículas. A primeira é uma necessidade clara na física da matéria condensada , em que tipicamente o número de partículas é na ordem de número de Avogadro (6.0221415 x 10 23). A segunda motivação para o problema de muitas partículas surge da física de partículas eo desejo de incorporar os efeitos da relatividade especial . Se alguém tenta incluir o relativista a energia restante na equação acima, o resultado é tanto a Equação de Klein-Gordon ou o Equação de Dirac. No entanto, essas equações têm muitas qualidades insatisfatórios; por exemplo, eles possuem energia valores próprios , que se estendem para -∞, de modo que parece haver nenhuma definição de um fácil estado fundamental. Acontece que essas inconsistências surgem de descurar a possibilidade de criar dinamicamente ou destruir partículas, o que é um aspecto crucial da relatividade. Einstein famoso relação massa-energia prevê que as partículas suficientemente maciças pode decair em várias partículas mais leves, e suficientemente partículas energéticas podem se combinar para formar partículas maciças. Por exemplo, um elétron e um pósitrons pode aniquilar uns aos outros para criar fótons . Assim, uma teoria quântica relativista consistente deve ser formulada como uma teoria de muitas partículas.
Além disso, vamos supor que o  partículas têm indistinguíveis. Como descrito no artigo sobre partículas idênticas, isto implica que o estado de todo o sistema deve ser ou simétricos ( bósons) ou (antisymmetric férmions), quando as coordenadas de suas partículas constituintes são trocados. Estes estados de multi-partículas são bastante complicado para escrever. Por exemplo, o estado quântico de um sistema geral de
partículas têm indistinguíveis. Como descrito no artigo sobre partículas idênticas, isto implica que o estado de todo o sistema deve ser ou simétricos ( bósons) ou (antisymmetric férmions), quando as coordenadas de suas partículas constituintes são trocados. Estes estados de multi-partículas são bastante complicado para escrever. Por exemplo, o estado quântico de um sistema geral de  bósons é escrito como
bósons é escrito como
onde  são os estados de partícula única,
são os estados de partícula única,  é o número de partículas de estado de ocupação
é o número de partículas de estado de ocupação  Ea soma é tomada sobre todas as possíveis permutações
Ea soma é tomada sobre todas as possíveis permutações  agindo em
agindo em  elementos. Em geral, este é uma soma de
elementos. Em geral, este é uma soma de 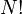 (
(  fatorial ) termos distintos, que rapidamente torna-se incontrolável como
fatorial ) termos distintos, que rapidamente torna-se incontrolável como  aumenta. A maneira de simplificar esse problema é transformá-lo em uma teoria quântica de campos.
aumenta. A maneira de simplificar esse problema é transformá-lo em uma teoria quântica de campos.
Segunda quantização
Nesta seção, iremos descrever um método para a construção de uma teoria quântica de campos chamado segunda quantização. Isso basicamente envolve a escolha de uma forma de indexar os graus de liberdade da mecânica quântica no espaço de vários estados idênticos de partículas. Ele baseia-se na Formulação hamiltoniana da mecânica quântica; Existem várias outras abordagens, tais como a Caminho feynman integrante, que utiliza um Formulação de Lagrange. Para uma visão geral, consulte o artigo sobre quantização.
Segunda quantização de bósons
Para simplificar, vamos primeiro discutir segunda quantização para bósons, que formam estados quânticos perfeitamente simétricos. Vamos denotar as ortogonais entre si, estados de partícula única por  e assim por diante. Por exemplo, o estado 3-partícula com partícula em um estado
e assim por diante. Por exemplo, o estado 3-partícula com partícula em um estado  e dois no estado
e dois no estado 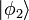 é
é
O primeiro passo na segunda quantização é a de expressar tais estados quânticos em termos de números de ocupação, listando o número de partículas que ocupam cada um dos estados de partícula única 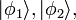 etc. Isto é simplesmente uma outra forma de rotular os estados. Por exemplo, o estado 3-partícula acima é denotado como
etc. Isto é simplesmente uma outra forma de rotular os estados. Por exemplo, o estado 3-partícula acima é denotado como
O próximo passo é expandir o  espaço de estado -particle para incluir os espaços estatais para todos os valores possíveis de
espaço de estado -particle para incluir os espaços estatais para todos os valores possíveis de  . Este espaço de estado estendido, conhecido como um Espaço de Fock, é constituído pelo espaço de estado de um sistema sem partículas (o chamado estado de vácuo), mais o espaço de estados de um sistema de 1-partícula, mais o espaço de estados de um sistema de 2-partícula, e assim por diante. É fácil de ver que há uma correspondência de um-para-um entre a representação número de ocupação e estados boson válidos no espaço de Fock.
. Este espaço de estado estendido, conhecido como um Espaço de Fock, é constituído pelo espaço de estado de um sistema sem partículas (o chamado estado de vácuo), mais o espaço de estados de um sistema de 1-partícula, mais o espaço de estados de um sistema de 2-partícula, e assim por diante. É fácil de ver que há uma correspondência de um-para-um entre a representação número de ocupação e estados boson válidos no espaço de Fock.
Neste ponto, o sistema mecânico quântico tornou-se um campo quântico no sentido em que descrito acima. Graus elementares do campo de liberdade são os números de ocupação, e cada número de ocupação é indexada por um número  , Indicando que os estados de partícula única
, Indicando que os estados de partícula única 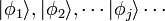 ela se refere.
ela se refere.
As propriedades desse campo quântico pode ser explorado através da definição operadores de criação e aniquilação, que adicionam partículas e subtrair. Eles são análogos a "escada operadores" na quantum problema oscilador harmônico, que adicionados e subtraídos quanta energia. No entanto, estes operadores, literalmente, criar e aniquilar partículas de um determinado estado quântico. O operador aniquilação bosônico  e operador de criação
e operador de criação  tem os seguintes efeitos:
tem os seguintes efeitos:
Pode ser demonstrado que estes são os operadores no sentido da mecânica quântica habitual, ou seja, operadores lineares que actuam sobre o espaço de Fock. Além disso, eles são de fato Conjugados hermitianas, o que justifica a nossa maneira de tê-los escrito. Eles podem ser mostrados para obedecer à relação de comutação
onde  representa o Kronecker delta. Estes são precisamente as relações obedecidas pelos operadores de escada para um conjunto infinito de independente osciladores harmônicos quânticos, um para cada estado de uma única partícula. Adicionando ou removendo bósons de cada Estado é, portanto, análogo ao excitante ou emocionante de-um quantum de energia em um oscilador harmônico.
representa o Kronecker delta. Estes são precisamente as relações obedecidas pelos operadores de escada para um conjunto infinito de independente osciladores harmônicos quânticos, um para cada estado de uma única partícula. Adicionando ou removendo bósons de cada Estado é, portanto, análogo ao excitante ou emocionante de-um quantum de energia em um oscilador harmônico.
O Hamiltoniano do campo quântico (que, por meio da Equação de Schrödinger, determina sua dinâmica) pode ser escrita em termos de operadores de criação e aniquilação. Por exemplo, o hamiltoniano de um campo de livres (sem interacção) bósons é
onde 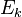 é a energia do
é a energia do  -th eigenstate energia de uma única partícula. Note que
-th eigenstate energia de uma única partícula. Note que
 .
.
Segunda quantização de férmions
Acontece que uma definição diferente de criação e aniquilação deve ser utilizado para descrever férmions. De acordo com Princípio de exclusão de Pauli, férmions não podem compartilhar estados quânticos, para que seus números de ocupação  só pode assumir o valor 0 ou 1. Os operadores de aniquilação fermiônicas
só pode assumir o valor 0 ou 1. Os operadores de aniquilação fermiônicas  e operadores de criação
e operadores de criação 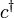 são definidos pela
são definidos pela
Estes obedecer a uma anticommutation relação:
Pode-se notar com este que a aplicação de um operador de criação fermionic duas vezes dá zero, por isso é impossível para as partículas de compartilhar estados de partícula única, em conformidade com o princípio da exclusão.
Operadores de campo
Temos mencionado anteriormente que não pode haver mais de uma maneira de indexar os graus de liberdade em um campo quântico. Segundo índices de quantificação do campo enumerando os de partícula única estados quânticos. No entanto, como já vimos, é mais natural pensar em um "campo", tais como o campo eletromagnético, como um conjunto de graus de liberdade indexados pela posição.
Para este fim, podemos definir operadores de campo que criar ou destruir uma partícula em um determinado ponto no espaço. Em física de partículas, estes operadores acabam por ser mais conveniente para trabalhar, porque eles tornam mais fácil para formular teorias que satisfazem as exigências da relatividade.
Estados Single-partículas são normalmente enumerados em termos da sua momentos (como no partícula em um problema de caixa.) Podemos construir operadores de campo, aplicando a Transformada de Fourier para os operadores de criação e aniquilação para estes estados. Por exemplo, o operador de campo aniquilação bosônico  é
é
Os operadores de campo bosônicos obedecer à relação de comutação
onde  representa o Delta de Dirac. Como antes, as relações fermiônicas são os mesmos, com os comutadores substituídos por anticommutators.
representa o Delta de Dirac. Como antes, as relações fermiônicas são os mesmos, com os comutadores substituídos por anticommutators.
Deve-se ressaltar que o operador de campo não é a mesma coisa que uma função de onda de partícula única. O primeiro é um operador que actua sobre o espaço de Fock, e este último é apenas um campo escalar. No entanto, elas estão intimamente relacionados, e são, de facto geralmente denotada com o mesmo símbolo. Se temos um Hamiltoniano com uma representação do espaço, dizem
onde os índices 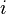 e
e  atropelar todas as partículas, então a teoria de campo é hamiltoniano
atropelar todas as partículas, então a teoria de campo é hamiltoniano
Isso se parece muito com uma expressão para o valor esperado da energia, com  desempenhando o papel da função de onda. Essa relação entre os operadores de campo e wavefunctions torna muito fácil para formular teorias de campo a partir de Hamiltonians projetada de espaço.
desempenhando o papel da função de onda. Essa relação entre os operadores de campo e wavefunctions torna muito fácil para formular teorias de campo a partir de Hamiltonians projetada de espaço.
Implicações da teoria quântica de campos
Unificação de campos e partículas
O procedimento de "segunda quantização" que temos delineado na seção anterior leva um conjunto de de partícula única estados quânticos como ponto de partida. Às vezes, é impossível definir tais estados de partícula única, e deve-se proceder diretamente à teoria quântica de campos. Por exemplo, uma teoria quântica da campo electromagnético deverá ser uma teoria quântica, porque é impossível (por várias razões) para definir um wavefunction para um único fóton . Em tais situações, a teoria quântica de campo pode ser construída examinando as propriedades mecânicas do campo clássica e adivinhar o correspondente teoria quântica. As teorias de campos obtidos deste modo tem as mesmas propriedades que as obtidas usando segunda quantização, tais como criação bem definida e operadores de aniquilação obedecendo relações de comutação ou anticommutation.
Teoria quântica de campos, portanto, fornece uma estrutura unificada para descrever "campo-como" objetos (como o campo eletromagnético, cuja excitações são fótons) e objetos "partícula-like" (como os elétrons, que são tratados como excitações de um campo de elétrons subjacente ).
Significado físico de partículas indistinguibilidade
O segundo procedimento de quantização depende de forma crucial as partículas sendo idêntico. Nós não teria sido capaz de construir uma teoria do campo quântico de um sistema de muitas partículas distinguíveis, porque não teria havido nenhuma maneira de separar e indexar os graus de liberdade.
Muitos físicos preferem tomar a interpretação inversa, o que é que a teoria quântica de campos explica o que são partículas idênticas. Na mecânica quântica comum, não há muita motivação teórica para a utilização simétrica (bosônico) ou antisimétricos (férmions) estados, ea necessidade de tais estados é simplesmente considerada como um fato empírico. Do ponto de vista da teoria quântica de campos, as partículas são idênticas se e somente se eles são excitações do mesmo campo quântico subjacente. Assim, a pergunta "por que todos os elétrons idênticos?" surge erroneamente sobre elétrons individuais como objetos fundamentais, quando na verdade ele é apenas o campo de elétron que é fundamental.
Conservação de partículas e não-conservação
Durante segunda quantização, começamos com um espaço hamiltoniano e estado descrevendo um número fixo de partículas (  ), E terminou com um Hamiltoniano e espaço de estado para um número arbitrário de partículas. É claro que, em muitas situações comuns
), E terminou com um Hamiltoniano e espaço de estado para um número arbitrário de partículas. É claro que, em muitas situações comuns  é uma quantidade importante e perfeitamente bem definida, por exemplo, se estamos a descrever um gás de átomos selados em uma caixa. Do ponto de vista da teoria quântica de campos, tais situações são descritos por estados quânticos que são auto-estados do operador de número
é uma quantidade importante e perfeitamente bem definida, por exemplo, se estamos a descrever um gás de átomos selados em uma caixa. Do ponto de vista da teoria quântica de campos, tais situações são descritos por estados quânticos que são auto-estados do operador de número  , Que mede o número total de partículas presentes. Como acontece com qualquer quantum observáveis mecânica,
, Que mede o número total de partículas presentes. Como acontece com qualquer quantum observáveis mecânica,  é conservada se comuta com a Hamiltoniana. Nesse caso, o estado quântico está preso no
é conservada se comuta com a Hamiltoniana. Nesse caso, o estado quântico está preso no  -particle subespaço do espaço de Fock total ea situação poderia igualmente bem ser descrito por comum
-particle subespaço do espaço de Fock total ea situação poderia igualmente bem ser descrito por comum  mecânica quântica -particle.
mecânica quântica -particle.
Por exemplo, podemos ver que a Hamiltoniana livre de Higgs descrito acima conserva o número de partículas. Sempre que o hamiltoniano opera em um estado, cada partícula destruído por um operador aniquilação  é imediatamente colocado de volta pelo operador criação
é imediatamente colocado de volta pelo operador criação 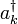 .
.
Por outro lado, é possível, e de facto comum, para encontrar estados quânticos que não são de autoestados  , Que não tem o número de partículas bem definidas. Esses estados são difíceis ou impossíveis de lidar com a mecânica quântica comuns, mas eles podem ser facilmente descrito em teoria quântica de campos como superposições quânticas de estados com diferentes valores de
, Que não tem o número de partículas bem definidas. Esses estados são difíceis ou impossíveis de lidar com a mecânica quântica comuns, mas eles podem ser facilmente descrito em teoria quântica de campos como superposições quânticas de estados com diferentes valores de  . Por exemplo, suponha que temos um campo bosônico cujas partículas pode ser criada ou destruída por interações com um campo fermiônico. O Hamiltoniano do sistema combinado seria dada pelos Hamiltonians do bóson livre e campos de férmions livres, além de uma "energia potencial" termo como
. Por exemplo, suponha que temos um campo bosônico cujas partículas pode ser criada ou destruída por interações com um campo fermiônico. O Hamiltoniano do sistema combinado seria dada pelos Hamiltonians do bóson livre e campos de férmions livres, além de uma "energia potencial" termo como
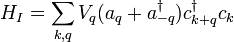 ,
,
onde 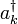 e
e  denota os operadores de criação e aniquilação bosônicos,
denota os operadores de criação e aniquilação bosônicos,  e
e  denota os operadores de criação e aniquilação fermiônicas, e
denota os operadores de criação e aniquilação fermiônicas, e 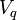 é um parâmetro que descreve a força da interacção. Este "termo de interação", descreve processos em que um fermion no estado
é um parâmetro que descreve a força da interacção. Este "termo de interação", descreve processos em que um fermion no estado  ou absorve ou emite um bóson, assim, ser expulso em uma eigenstate diferente
ou absorve ou emite um bóson, assim, ser expulso em uma eigenstate diferente  . (Na verdade, este tipo de Hamiltoniano é usado para descrever a interacção entre elétrons de condução e fônons em metais . A interacção entre os electrões e os fotões é tratado de uma forma semelhante, mas é um pouco mais complicado, porque o papel de rotação deve ser levado em conta.) Uma coisa a notar aqui é que, mesmo que começar com um número fixo de bósons, que normalmente vai acabar com uma superposição de estados com diferentes números de bósons em momentos posteriores. O número de fermiones, no entanto, é conservada no caso presente.
. (Na verdade, este tipo de Hamiltoniano é usado para descrever a interacção entre elétrons de condução e fônons em metais . A interacção entre os electrões e os fotões é tratado de uma forma semelhante, mas é um pouco mais complicado, porque o papel de rotação deve ser levado em conta.) Uma coisa a notar aqui é que, mesmo que começar com um número fixo de bósons, que normalmente vai acabar com uma superposição de estados com diferentes números de bósons em momentos posteriores. O número de fermiones, no entanto, é conservada no caso presente.
Em física da matéria condensada , os estados com o número de partículas mal definidas são particularmente importantes para descrever os vários superfluidos. Muitas das características definidoras de um superfluido surgir a partir da noção de que o seu estado quântico é uma superposição de estados com diferentes números de partículas.
Abordagens axiomáticas
A descrição anterior da teoria quântica de campos segue o espírito em que a maioria físicos abordar o assunto. No entanto, não é matematicamente rigorosa. Ao longo das últimas décadas, tem havido muitas tentativas de colocar a teoria quântica de campos em um fundamento firme matemática através da formulação de um conjunto de axiomas para ele. Estas tentativas se dividem em duas grandes classes.
A primeira classe de axiomas, proposto pela primeira vez durante o 1950, incluem o Wightman, Osterwalder-Schrader, e Sistemas Haag-Kastler. Eles tentaram formalizar noção de um "campo valor de operador" dos físicos dentro do contexto da análise funcional, e sucesso limitado apreciado. Foi possível provar que qualquer teoria quântica de campos satisfazem esses axiomas satisfeito certos teoremas gerais, tais como o spin-estatísticas teorema eo CPT teorema. Infelizmente, revelou-se extraordinariamente difícil para mostrar que qualquer teoria de campo realista, incluindo o Modelo Padrão , satisfeito estes axiomas. A maioria das teorias que poderiam ser tratadas com estes axiomas analíticos eram fisicamente trivial, sendo restrita a-dimensões baixas e falta dinâmica interessantes. A construção de teorias que satisfaçam um destes conjuntos de axiomas cai no campo de teoria quântica de campos construtivo. Importante trabalho foi feito nesta área no 1970 por Segal, Glimm, Jaffe e outros.
Durante o 1980, um segundo conjunto de axiomas com base em geométricas idéias foi proposto. Esta linha de investigação, o que limita a sua atenção para uma determinada classe de teorias quânticas de campos conhecidos como teorias de campo quânticos topológicos, associa-se mais estreitamente com Michael Atiyah e Graeme Segal, e, nomeadamente, foi expandida por Edward Witten, Richard Borcherds, e Maxim Kontsevich. No entanto, as teorias quânticas de campo mais fisicamente relevantes, tais como o Modelo Padrão , não são teorias de campo quânticos topológicos; a teoria quântica de campos do efeito Hall quântico fracionário é uma notável exceção. O principal impacto da teoria quântica de campos topológica axiomático foi em matemática, com importantes aplicações em teoria da representação, topologia algébrica e geometria diferencial .
Encontrar os axiomas adequados para a teoria quântica de campos ainda é um problema em aberto e difícil em matemática. Um dos Millennium Prize Problems-provando a existência de um gap de massa no Yang-Mills teoria está ligada a esta questão.
Os fenômenos associados com a teoria quântica de campos
Na parte anterior do artigo, descrevemos as propriedades mais gerais da teoria quântica de campos. Algumas das teorias quânticas de campos estudados em vários campos da física teórica possuem propriedades especiais adicionais, como renormalizabilidade, calibre de simetria, e supersimetria. Estes são descritos nas secções seguintes.
Renormalization
No início da história da teoria quântica de campos, verificou-se que muitos cálculos aparentemente inócuos, como o mudança perturbativa na energia do electrão devido à presença do campo electromagnético, dão resultados infinitas. Muitos destes problemas estão relacionados com falhas em eletrodinâmica clássica que foram identificadas (mas não resolvidos), tanto para trás como o século 19 , e eles basicamente derivam do fato de que muitas das supostas propriedades "intrínsecos" de um elétron estão vinculados ao campo eletromagnético com o qual interage. Para ilustrar isso, lembre-se a partir da discussão anterior que o hamiltoniano interação entre dois campos quânticos, como o campo de elétrons e do campo eletromagnético, não precisa conservar o número de partículas. Assim, mesmo que começar com um único elétron e há fótons, o estado quântico irá evoluir rapidamente em uma superposição de estados que pode incluir um ou mais fótons. Portanto, a energia transportada por que "single" de elétron-its auto-energia não é simplesmente o valor "nua", mas inclui também a energia contida em uma nuvem de atendente de fótons. Quando esse auto de energia é calculado, verifica-se que a contribuição de fótons possuindo arbitrariamente altas energias (ou, de forma equivalente, arbitrariamente curto comprimentos de onda) conduz a um valor formalmente infinito.
A solução para este problema, em primeiro lugar determinado pela Julian Schwinger, é chamado renormalização . A idéia é impor uma " corte "para a contribuição fotónica, por exemplo, postulando que fotões não pode possuir energias acima de algum valor extremamente elevado. Qualquer quantidade que deseja calcular, tal como a energia de repouso, é agora finito, mas dependente do ponto de corte. Em seguida, reformulação do resultado em termos quantidades de fisicamente observáveis tais como a massa observada de electrões, em vez de quantidades não observáveis tais como a energia de corte e a massa de electrões nu. O resultado final é independente de todos os pormenores do procedimento de corte, incluindo o valor da energia de corte, desde a processos relevantes ocorrem a energias muito abaixo do ponto de corte.
O procedimento de renormalização só funciona para uma determinada classe de teorias quânticas de campo, chamado de teorias quânticas de campo renormalizáveis. O Modelo Padrão da física de partículas é renormalizável, e por isso são suas teorias componentes ( eletrodinâmica quântica / teoria eletrofraca e cromodinâmica quântica). De acordo com a teoria do grupo de renormalização, cada teoria renormalizável um limite de baixa energia única (ou seja, o chamado " teoria eficaz campo ") para uma ampla gama de teorias de alta energia. renormalizável teorias são, por conseguinte, independente da natureza precisa dos fenómenos de alta energia subjacentes.
Liberdade calibre
A teoria de gauge é uma teoria que admite um simetria com um parâmetro local. Por exemplo, em cada quântica teoria global fase do função de onda é arbitrária e não representa algo físico. Consequentemente, a teoria é invariante sob uma mudança global das fases (adicionando uma constante para a fase de todas as funções de onda, em todos os lugares); isto é um simetria global. Em eletrodinâmica quântica, a teoria também é invariante sob uma alteração local de fase, ou seja - pode-se mudar a fase de tudo funções de onda de modo que a mudança pode ser diferente em cada ponto espaço-tempo. Isto é um simetria local. No entanto, para que uma estrutura bem definida derivado operador de existir, deve-se introduzir um novo campo, o campo indicador, que também se transforma, para que a mudança local de variáveis (fase, no nosso exemplo) não para afectar o derivado. Em eletrodinâmica quântica este campo indicador é o campo eletromagnético. A mudança de bitola local das variáveis é denominado calibrar a transformação.
Em teoria quântica de campos as excitações dos campos representam partículas. A partícula associada com excitações do campo indicador é o calibre Higgs, que é a de fotões no caso de eletrodinâmica quântica.
O graus de liberdade em teoria quântica de campos são flutuações locais dos campos. A existência de um medidor de simetria reduz o número de graus de liberdade, simplesmente porque algumas flutuações dos campos pode ser transformado para zero por medir transformações, assim eles são equivalentes a não ter flutuações em tudo, e, portanto, eles não têm qualquer significado físico. Tais flutuações são geralmente chamados de "não-físicos graus de liberdade" ou artefatos de calibre; geralmente alguns deles têm um negativo norma, tornando-os inadequados para uma teoria consistente. Portanto, se uma teoria clássica dos campos tem uma simetria de calibre, então sua versão quantizada (ou seja, a teoria quântica de campos correspondente) terá esta simetria. Em outras palavras, uma simetria de calibre não pode ter um quantum anomalia. Se uma simetria de calibre é anômala (ou seja, não mantido na teoria quântica), então a teoria não é consistente: por exemplo, na eletrodinâmica quântica, se tivesse havido um medidor de anomalia, isso exigiria a aparência de fótons com longitudinal polarização e polarização no tempo direção, tendo este último um negativo norma, tornando a teoria inconsistente; Outra possibilidade seria a de que esses fotões que aparecem apenas em processos intermédios, mas não nos produtos finais de qualquer interacção, tornando a teoria não unitária e novamente inconsistente (ver teorema óptica).
Em geral, o transformações de calibre de uma teoria consistem várias transformações diferentes, que podem não ser comutativa . Essas transformações estão juntos descrito por um objeto matemático conhecido como um grupo de calibre. infinitesimais transformações de calibre são o grupo de calibre geradores. Portanto, o número de bósons é o grupo de dimensão (ou seja, número de geradores que formam uma base).
Todo interações fundamentais da natureza são descritos por teorias de gauge. Estes são:
- Eletrodinâmica quântica, cujabitola transformação é uma alteração local de fase, de modo que ogrupo indicador éU (1). O bóson de calibre é ofóton.
- Cromodinâmica quântica, cujabitola grupo é SU (3). O bósons são oito glúons.
- O Teoria electroweak, cujogrupo de gauge é
 (umproduto direto daU (1) eSU (2)).
(umproduto direto daU (1) eSU (2)). - Gravidade, cuja teoria clássica érelatividade geral, admite o princípio da equivalência, que é uma forma de calibre simetria.
Supersimetria
Supersimetria assume que cada fundamentais fermion tem uma Superpartner que é um bóson e vice-versa. Foi introduzida a fim de resolver o chamado Hierarquia problema, isto é, para explicar por que as partículas não protegidos por qualquer simetria (como o bóson de Higgs) não receber correções radiativas a sua massa conduzi-lo para as escalas maiores (GUT, Planck ...). Foi logo percebeu-se que a supersimetria tem outras propriedades interessantes: sua versão aferida é uma extensão da relatividade geral ( supergravity), e é um ingrediente chave para a consistência da teoria das cordas .
A forma como a supersimetria protege as hierarquias é a seguinte: uma vez que para cada partícula existe uma Superpartner com a mesma massa, qualquer circuito em uma correção radiativo é cancelado pelo circuito correspondente à sua Superpartner, tornando o finito UV teoria.
Desde ainda não foram observados superparceiros, se a supersimetria existe deve ser quebrada (por meio de um termo suave chamada, que quebra a supersimetria sem arruinar seus votos recursos). Os modelos mais simples desta quebra exigem que a energia dos superparceiros não ser demasiado elevada; nestes casos, supersymmetry está prevista para ser observado por experiências no Large Hadron Collider.
![\ Left [\ frac {| \ mathbf {p} | ^ 2}} {2m + V (\ mathbf {r}) \ right] | \ psi (t) \ rang = i \ hbar \ frac {\ partial} { \ partial t} | \ psi (t) \ rang,](../../images/261/26195.png)
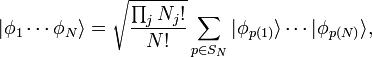
![\ Frac {1} {\ sqrt {3}} \ left [| \ phi_1 \ rang | \ phi_2 \ rang | \ phi_2 \ rang + | \ phi_2 \ rang | \ phi_1 \ rang | \ phi_2 \ rang + | \ phi_2 \ tocou | \ phi_2 \ rang | \ phi_1 \ rang \ right].](../../images/262/26203.png)
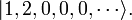


![\ Left [a_i, a_j \ right] = 0 \ quad \ quad \ left [a_i ^ \ punhal, a_j ^ \ punhal \ right] = 0 \ quad \ quad \ left [a_i, a_j ^ \ punhal \ right] = \ delta_ {ij},](../../images/262/26211.png)


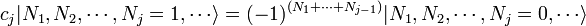

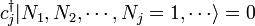
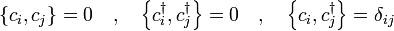

![\ Left [\ phi (\ mathbf {r}), \ phi (\ mathbf {r '}) \ right] = 0 \ quad \ quad \ left [\ phi ^ \ dagger (\ mathbf {r}), \ phi ^ \ dagger (\ mathbf {r '}) \ right] = 0 \ quad \ quad \ left [\ phi (\ mathbf {r}), \ phi ^ \ dagger (\ mathbf {r'}) \ right ] = \ delta ^ 3 (\ mathbf {R} - \ mathbf {r '})](../../images/262/26222.png)


