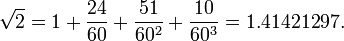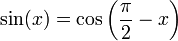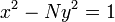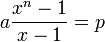La matemática india

Temas relacionados: Matemáticas

Antecedentes de las escuelas de Wikipedia

Organizar una selección Wikipedia para las escuelas en el mundo en desarrollo sin acceso a Internet era una iniciativa de SOS Children. Haga clic aquí para obtener información sobre el apadrinamiento de niños.

Historia de la ciencia

Fondo Teorías / sociología Historiografía Pseudociencia
Por época En las primeras culturas en la Antigüedad Clásica En la Edad Media En el Renacimiento Revolución científica Romanticismo en la ciencia
Por cultura Africano Bizantino Chino Indio Islámico Coreano Mexicano Persa
Ciencias Naturales Astronomía Biología Botánica Química Ecología Evolución Geología Geofísica Paleontología Física
Matemáticas Álgebra Cálculo Combinatoria Geometría Lógica Probabilidad Estadística Trigonometría
Ciencias Sociales Antropología Ciencias económicas Geografía Lingüística Ciencias Políticas Psicología Sociología Sostenibilidad
Tecnología Las ciencias agrícolas Ciencias de la Computación Ciencia de los Materiales Ciencia militar
Medicina Medicina alternativa Anatomía La anestesia (general) Bioquímica Biotecnología Cáncer Cardiología (invasiva y de intervención) Dermatología Embriología Endocrinología Genética Inmunología Diagnóstico médico Biología molecular Neurología Neurociencia Nutrición Patología Psiquiatría Cirugía Virología
Páginas de navegación Líneas de tiempo Portal Categorías

Matemáticas indias -que aquí es la matemática que surgieron en El sur de Asia desde la antigüedad hasta el final de la 18 ª siglo tuvo sus inicios en la Edad de Bronce civilización del valle del Indo (2600-1900 BCE) y la Edad del Hierro Cultura védica (1500-500 aC). En la época clásica de las matemáticas indias ( 400 CE a 1200 CE), las contribuciones importantes fueron hechas por eruditos como Aryabhatta, Brahmagupta, y Bhaskara II. Matemáticos indios hicieron primeras contribuciones al estudio del sistema decimal número , cero , los números negativos , la aritmética y el álgebra . Además, la trigonometría , habiendo evolucionado en el Mundo helenístico y de haber sido introducido en la antigua India a través de la traducción de griego obras, era más avanzada en la India, y, en particular, las definiciones modernas de seno y coseno se desarrollaron allí. Estos conceptos matemáticos fueron transmitidas al Medio Oriente , de China , y Europa y dio lugar a los nuevos acontecimientos que ahora forman los cimientos de muchas áreas de las matemáticas.

Trabajos matemáticos indios antiguos y medievales, todos compuestos en sánscrito , por lo general consistían en una sección de sutras en el que un conjunto de reglas o problemas se manifestaron con gran economía en el verso con el fin de ayudar a la memorización de un estudiante. Esto fue seguido por una segunda sección consta de un comentario en prosa (a veces múltiples comentarios por diferentes eruditos) que explica el problema con más detalle y proporciona justificación de la solución. En la sección de la prosa, la forma (y por tanto su memorización) no se consideró tan importante como las ideas involucradas. Todos los trabajos matemáticos fueron transmitidas oralmente hasta que aproximadamente 500 aC; a partir de entonces, que fueron transmitidos en forma oral y en forma manuscrita. El documento matemático más antiguo existente producido en el subcontinente indio es la corteza de abedul Bakhshali manuscrito, descubierto en 1881 en el pueblo de Bakhshali, cerca Peshawar (actual Pakistán ) y es probable que desde el siglo VII.

Un punto de referencia más adelante en las matemáticas de la India fue el desarrollo de la desarrollos en serie de funciones trigonométricas (seno, coseno, y arco tangente) por los matemáticos de la Escuela de Kerala en el CE del siglo XV. Su trabajo notable, completado dos siglos antes de la invención del cálculo en Europa, siempre lo que hoy se considera el primer ejemplo de una serie de potencias (aparte de la serie geométrica). Sin embargo, no formularon una teoría sistemática de la diferenciación y la integración , ni hay ninguna prueba directa de sus resultados que se transmite fuera de Kerala .

Los campos de la matemática india

Algunas de las áreas de las matemáticas estudiadas en la antigua y medieval India incluyen los siguientes:

Aritmética : Sistema decimal, los números negativos (véase Brahmagupta), Zero (ver Numeración arábiga), el moderno notación posicional sistema de numeración , Los números de coma flotante (ver Escuela de Kerala), teoría de números , Infinito (ver Yajur Veda), Números transfinitos, números irracionales (véase Sulba Sutras)
Geometría : Las raíces cuadradas (ver Bakhshali aproximación), Raíces cúbicas (véase Mahavira), Ternas pitagóricas (ver Sutras Sulba; Baudhayana y Apastamba estado el teorema de Pitágoras sin pruebas), Transformación (ver Panini), el triángulo de Pascal (ver Pingala)
Álgebra : Ecuaciones cuadráticas (ver Sulba Sutras, Aryabhata, y Brahmagupta), Ecuaciones cúbicas (ver Mahavira y Bhaskara), Ecuaciones de cuarto grado (ecuaciones bicuadráticos; ver Mahavira y Bhaskara)
La lógica matemática: Gramáticas formales, la teoría del lenguaje formal, el Forma Panini-Backus (ver Panini), La recursividad (ver Panini)
Matemáticas generales: los números de Fibonacci (ver Pingala), las formas más tempranas de código Morse (véase Pingala), logaritmos , índices (ver Jaina matemáticas), Algoritmos , Algoritmo (véase Aryabhata y Brahmagupta)
Trigonometría : funciones trigonométricas (ver Surya Siddhanta y Aryabhata), Series trigonométricas (ver Madhava y Escuela de Kerala)

Matemáticas indias muestran muchas maneras diferentes de la cultura india.

Harappa Matemáticas (2600 aC - 1700 aC)

La evidencia más temprana del uso de las matemáticas en Asia del Sur se encuentra en los artefactos de la civilización del valle del Indo (IVC), también llamada la civilización Harappa. Las excavaciones en Harappa, Mohenjo-Daro (Pakistán) y otros lugares en el río Indus valle han descubierto indicios de la utilización de las matemáticas prácticas. La gente de la IVC fabrican ladrillos cuyas dimensiones eran en la proporción 4: 2: 1, considerado favorable para la estabilidad de una estructura de ladrillo. Se utilizó un sistema estandarizado de pesos basados en las proporciones: 1/20, 1/10, 1/5, 1/2, 1, 2, 5, 10, 20, 50, 100, 200, y 500, con la unidad peso equivalente a aproximadamente 28 gramos (y aproximadamente igual a la oz Inglés o uncia griego). Se fabrican en serie en pesos regulares geométricas formas, que incluían hexaedros, barriles, conos, y cilindros, lo que demuestra el conocimiento de básico geometría .

Los habitantes de la civilización del Indo también intentaron homogeneizar la medición de la longitud de un alto grado de precisión. Diseñaron un -cuya unidad-gobernante del Mohenjo-Daro gobernante de longitud (aproximadamente 1,32 pulgadas o 3,4 centímetros) se dividió en diez partes iguales. Ladrillos fabricados en la antigua Mohenjo-Daro menudo tenían dimensiones que eran múltiplos enteros de esta unidad de longitud.

La Tradición Oral Matemática

Los matemáticos de la antigua y principios de la India medieval eran casi todos sánscrito panditas (paṇḍita "aprendidas hombre"), que fueron capacitados en el idioma sánscrito y la literatura, y poseía "un tronco común de conocimientos en gramática ( Vyākaraṇa), exégesis ( mimamsa) y la lógica ( nyāya). "La memorización de" lo que se escucha "( śruti en sánscrito) a través de la recitación desempeñó un papel importante en la transmisión de los textos sagrados en la India antigua. Memorización y recitación también se utilizó para transmitir obras filosóficas y literarias, así como tratados sobre el ritual y la gramática. Los estudiosos modernos de la antigua India han tomado nota de los "logros verdaderamente notables de los panditas indios que han conservado enormemente textos voluminosos por vía oral durante milenios."

Estilos de memorización

Energía prodigiosa se gastó por la antigua cultura de la India para garantizar que estos textos fueron transmitidos de generación en generación con fidelidad excesiva. Por ejemplo, la memorización de lo sagrado Vedas incluye hasta once formas de recitación del mismo texto. Los textos fueron posteriormente "prueba de lectura" mediante la comparación de las diferentes versiones citados. Formas de recitación incluyeron la Jata-pāṭha (literalmente "la recitación de malla") en el que cada dos palabras adyacentes en el texto se recitaban primero en su orden original, y luego repiten en el orden inverso, y finalmente repitieron de nuevo en el orden original. Así, la recitación procedió como:

word1word2, word2word1, word1word2; word2word3, word3word2, word2word3; ...

En otra forma de recitación, dvaja-pāṭha (literalmente "la recitación de la bandera") una secuencia de N palabras se recitó (y memorizado) por el emparejamiento de las dos primeras y las dos últimas palabras y luego proceder como:

word1word2, palabra (N-1) wordN; word2word3, palabra (N-3) palabra (N-2); ...; palabra (N-1) wordN, word1word2;

La forma más compleja de la recitación, ghana-pāṭha (literalmente "la recitación densa"), de acuerdo con (. Filliozat 2004, p 139), tomó la forma:

word1word2, word2word1, word1word2word3, word3word2word1, word1word2word3; word2word3, word3word2, word2word3word4, word4word3word2, word2word3word4; ...

Que estos métodos han sido eficaces, es testificado por la preservación de los más antiguos textos religiosos de la India, la Ṛgvedá ( ca. 1500 BCE), como un solo texto, sin ningún tipo de variantes de lectura. Métodos similares se utilizaron para la memorización de textos matemáticos, cuya transmisión mantenido exclusivamente oral hasta el final de la Período védico (ca. 500 aC).

El sutra Género

La actividad matemática en la antigua India comenzó como parte de una "reflexión metodológica" en lo sagrado Vedas, que tomó la forma de obras denominado Vedangas, o, "Auxiliares del Veda" (siglo BCE septima-cuarta). La necesidad de conservar el sonido del texto sagrado mediante el uso de śikṣā ( fonética) y chandas ( métricas); para conservar su significado por el uso de Vyākaraṇa ( gramática) y nirukta ( etimología); y para llevar a cabo correctamente los ritos en el momento correcto por el uso de kalpa ( ritual) y Jyotisa ( astronomía ), dio lugar a las seis disciplinas de la Vedangas. Matemáticas surgió como parte de los últimos dos disciplinas, el ritual y la astronomía (que también incluía la astrología). Desde el Vedangas precedió inmediatamente el uso de la escritura en la antigua India, formaron el último de la literatura exclusivamente oral. Ellos se expresaron en forma mnemotécnica de alta compresión, la sūtra (literalmente, "hilo"):

Los conocedores de la sūtra saben como tener unos fonemas, siendo carente de ambigüedad, que contiene la esencia, frente a todo, estar sin pausa e inobjetable.

Extrema brevedad se logró a través de múltiples medios, que incluían el uso de puntos suspensivos "más allá de la tolerancia del lenguaje natural", el uso de nombres técnicos en lugar de los nombres más descriptivos, que coarte listas por sólo mencionar las primeras y últimas entradas, y el uso de marcadores y variables. Los sutras crean la impresión de que la comunicación a través del texto era "sólo una parte de toda la instrucción. El resto de la instrucción debe haber sido transmitido por la llamada Parampara Guru-shishya, 'sucesión ininterrumpida de maestro (gurú) para el estudiante (sisya),' y no fue abierta al público en general en secreto ", y tal vez incluso mantenido. La brevedad logrado en un sutra se demuestra en el siguiente ejemplo de la Baudhayana Sulba Sūtra (700 aC).

El diseño del altar del fuego interno en el Sulba Sūtra

El fuego-altar doméstico en el Período védico fue requerido por el ritual de tener una base cuadrada y estar constituido por cinco capas de ladrillos con 21 ladrillos en cada capa. Un método para construir el altar era dividir a un lado de la plaza en tres partes iguales con una cuerda o soga, para el próximo dividir el transversal (o perpendicular) lado en siete partes iguales, y por lo tanto sub-dividir el cuadrado en 21 rectángulos congruentes . Los ladrillos fueron diseñados para ser de la forma del rectángulo constituyente y la capa se ha creado. Para formar la siguiente capa, se utilizó la misma fórmula, pero los ladrillos fueron dispuesto transversalmente. El proceso se repitió tres veces más (con direcciones alternas) con el fin de completar la construcción. En el Baudhayana Sulba Sutra, este procedimiento se describe en las siguientes palabras:

"II.64. Después de dividir el quadri-lateral de cada siete, uno divide la transversal [cable] en tres.
II.65. En otra capa uno pone el [ladrillos] orientada hacia el norte ".

De acuerdo con (Filliozat 2004, p 144.), El oficiante construir el altar tiene sólo unas pocas herramientas y materiales a su disposición: una cuerda (. Sánscrito, rajju, f), dos clavijas (. Sánscrito, Sanku, m), y arcilla para hacer los ladrillos (sánscrito, iṣṭakā, f.). Concisión se logra en el Sutra, al no mencionar explícitamente lo que califica el adjetivo "transversal"; Sin embargo, a partir de la forma femenina de la (sánscrito) adjetivo usado, es fácil inferir de calificar "cordón". Del mismo modo, en la segunda estrofa, no se mencionan "ladrillos" de forma explícita, pero inferirse de nuevo por la forma plural femenina de "orientada hacia el norte." Por último, la primera estrofa, dice nunca de manera explícita que la primera capa de ladrillos están orientados en la dirección Este-Oeste, pero que también está implicada por la mención explícita de "orientada hacia el norte", en la segunda estrofa; para, si la orientación estaba destinado a ser el mismo en las dos capas, sería o bien no se menciona en absoluto o sólo se menciona en la primera estrofa. Todas estas inferencias son hechas por el oficiante mientras recuerda la fórmula de su memoria.

Período védico (1500 aC - 400 aC)

Los textos religiosos de la Período védico proporcionar evidencia para el uso de grandes números. En el momento de la última Veda, la Yajurvedasaṃhitā (1200-900 aC), los números de hasta $10 ^ {12}$ estaban siendo incluidos en los textos. Por ejemplo, el mantra (fórmula sacrificial) al final de la annahoma ("Rite-oblación de alimentos") realiza durante el aśvamedha ("sacrificio de caballo"), y pronunció justo antes-, during-, y justo después de la salida del sol, invoca potencias de diez de cien a un billón:

"Hail to SATA (" cien " $10 ^ 2$ ), Granizo a sahasra ("mil" $10 ^ 3$ ), Granizo a ayuta ("diez mil" $10 ^ 4$ ), Granizo a niyuta ("cientos de miles" $10 ^ 4$ ), Granizo a prayuta ("millones" $10 ^ 6$ ), Granizo a Arbuda ("diez millones" $10 ^ 7$ ), Granizo a nyarbuda ("cien millones" $10 ^ 8$ ), Granizo a samudra ("mil millones" $10 ^ 9$ , Literalmente "mar"), el granizo de Madhya ("diez mil millones" $10 ^ {10}$ , Literalmente "medio"), el granizo a anta ("cien mil millones" $10 ^ {11}$ , Lit., "fin"), el granizo a parārdha ("un billón" $10 ^ {12}$ lit., "más allá de las partes"), el granizo al alba (USAS), granizo al crepúsculo (vyuṣṭi), granizo a la que se va a subir (udeṣyat), granizo a la que va en aumento (Udyat), granizo a la que sólo se ha levantado (udita), granizo al cielo (svarga), granizo al mundo (loka), granizo a todos ".

La Satapatha Brahmana (9no siglo BCE) contiene normas para construcciones geométricas rituales que son similares a los Sutras Sulba.

Sulba Sūtras

La Sulba Sūtras (literalmente, "Aforismos de los acordes" en Sánscrito védico) (c. 700-400 aC reglas) Lista para la construcción de altares de fuego de sacrificio. La mayoría de los problemas matemáticos considerados en la primavera Sulba Sūtras de "una sola exigencia teológica", el de la construcción de altares de fuego que tienen diferentes formas pero compartan la misma zona. Se pidió a los altares a ser construida de cinco capas de ladrillo cocido, con la condición adicional de que cada capa consiste en 200 ladrillos y que no hay dos capas adyacentes tienen acuerdos congruentes de ladrillos.

De acuerdo con (Hayashi 2005, p. 363), los sutras Sulba contienen "la expresión verbal más antigua existente del Teorema de Pitágoras en el mundo, a pesar de que ya había sido conocido por la Babilonios antiguos ".

La cuerda diagonal (akṣṇayā-rajju) de un rectángulo (rectángulo) produce tanto que el flanco (pārśvamāni) y la horizontal (tiryaṇmānī) producir por separado ".

Desde la declaración es un sutra, se comprime y lo necesariamente las cuerdas producen no es elaborado, pero el contexto implica claramente las áreas cuadrados construidos en sus longitudes, y habría sido explicado que el maestro al alumno.

Contienen listas de Ternas pitagóricas, que son casos particulares de Ecuaciones diofánticas. También contienen declaraciones (que en retrospectiva que sabemos que es aproximado) sobre la cuadratura del círculo y "rodeando la plaza."

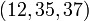Baudhayana (. C 8vo siglo BCE) compuso la Baudhayana Sulba Sutra, el más conocido Sulba Sutra, que contiene ejemplos de ternas pitagóricas simples, tales como: $(3, 4, 5)$ , $(5, 12, 13)$ , $(8, 15, 17)$ , $(7, 24, 25)$ Y $(12, 35, 37)$ así como una declaración del teorema de Pitágoras para los lados de un cuadrado: "La soga que se tiende a través de la diagonal de un cuadrado produce un área del doble del tamaño de la plaza original". También contiene la declaración general del teorema de Pitágoras (para los lados de un rectángulo): "La cuerda estirada a lo largo de la longitud de la diagonal de un rectángulo hace un área que los lados verticales y horizontales hacen juntos." Baudhayana da una fórmula para la raíz cuadrada de dos,

$\ Sqrt {2} = 1 + \ frac {1} {3} + \ frac {1} {3 \ cdot4} - \ frac {1} {3 \ cdot 4 \ cdot 34} \ aprox 1.4142156 \ cdots$

La fórmula es exacta hasta cinco cifras decimales, siendo el valor verdadero 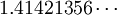$1.41421356 \ cdots$ Esta fórmula es similar en estructura a la fórmula que se encuentra en una tableta de mesopotámico del período paleobabilónico (1900-1600 C.):

$\ Sqrt {2} = 1 + \ frac {24} {60} + \ frac {51} {60 ^ 2} + \ frac {10} {60} ^ 3 = 1.41421297.$

que expresa $\ Sqrt {2}$ en el sistema sexagesimal, y que también es precisa hasta 5 decimales (después de redondeo).

Según el matemático SG Dani, la tablilla cuneiforme babilónica Ca. Plimpton 322 escrito 1850 BCE "contiene quince ternas pitagóricas con bastante grandes entradas, incluyendo (13500, 12709, 18541), que es un triple primitiva, lo que indica, en particular, que no era sofisticada comprensión sobre el tema" en Mesopotamia en el año 1850 BCE. "Dado que estas pastillas son anteriores al período Sulbasutras por varios siglos, teniendo en cuenta el aspecto contextual de algunos de los triples, es razonable esperar que la comprensión semejante hubiera estado allí en la India." Dani continúa diciendo:

"Como el principal objetivo de la Sulvasutras fue describir las construcciones de los altares y los principios geométricos que participan en ellos, el tema de ternas pitagóricas, incluso si hubiera sido bien entendida puede todavía no han aparecido en la Sulvasutras. La aparición de los triples en el Sulvasutras es comparable a las matemáticas que uno puede encontrar en un libro de introducción a la arquitectura o la otra área aplicada similar y no se correspondería directamente al conocimiento general sobre el tema en ese momento. Dado que, por desgracia, no se han encontrado otras fuentes contemporáneas puede que nunca sea posible resolver esta cuestión de manera satisfactoria ".

En los tres Sutras Sulba fueron compuestas. Los dos restantes, el Manava Sulba Sutra compuesta por Manava (fl. 750 a 650 aC) y la Apastamba Sulba Sutra, compuesta por Apastamba (c. 600 aC), contenía resultados similares a la Baudhayana Sulba Sutra.

Vyakarana

Un hito importante del período védico fue obra de Gramático sánscrito, Pāṇini (c. 520-460 aC). Su gramática incluye el uso temprano de la lógica booleana , de la nula del operador, y de gramáticas libres de contexto, e incluye un precursor de la Forma Backus-Naur (usado en la descripción de lenguajes de programación ).

Jaina Matemáticas (400 aC - 200 dC)

Aunque Jainismo como religión y filosofía es anterior a su exponente más famoso, Mahavira ( Siglo sexto antes de Cristo), quien fue contemporáneo de Gautama Buda , la mayoría de los textos de Jaina en topcs matemáticos fueron compuestas después del siglo 6 aC. Matemáticos Jaina son importantes históricamente como vínculos fundamentales entre las matemáticas del período védico y el de la "época clásica."

Una contribución histórica significativa de Jaina matemáticos yacía en su liberación de las matemáticas indias de sus limitaciones religiosas y rituales. En particular, su fascinación por la enumeración de números muy grandes y los infinitos , los llevó a clasificar los números en tres clases: enumerables, innumerables y infinito. No contento con una simple noción de infinito, que pasó a definir cinco tipos diferentes de infinito: el infinito en una dirección, lo infinito en dos direcciones, el infinito en el área, el infinito en todas partes, y el infinito perpetuamente. Además, los matemáticos Jaina idearon notaciones para potencias sencillas (y exponentes) de números como cuadrados y cubos, lo que les permitió definir sencilla ecuaciones algebraicas (beezganit samikaran). Matemáticos Jaina eran al parecer también el primero en utilizar la palabra shunya (literalmente vacío en sánscrito ) para referirse a cero. Más de un milenio más tarde, su denominación se convirtió en la palabra Inglés "cero" después de un tortuoso viaje de traducciones y transcripciones de la India a Europa. (Ver Zero: Etimología .)

Además de Surya Prajnapti, importante Jaina trabaja en matemáticas incluyen la Vaishali Ganit (c 3er siglo BCE.); la Sthananga Sutra (fl 300 aC - 200 dC.); la Anoyogdwar Sutra (fl 200 aC - 100 dC.); y la Satkhandagama (c. segundo siglo dC). Importantes matemáticos Jaina incluidos Bhadrabahu (d 298 aC.), El autor de dos trabajos astronómicos, la Bhadrabahavi-Samhita y un comentario sobre el Surya Prajinapti; Yativrisham Acharya (c 176 aC.), Autor de un texto matemático llamado Tiloyapannati; y Umasvati (c. 150 aC), que, aunque más conocido por sus influyentes escritos sobre filosofía y Jaina metafísica, compuso un trabajo matemático llamado Tattwarthadhigama-Sutra Bhashya.

Pingala

Entre otros estudiosos de este período que han contribuido a las matemáticas, la más notable es Pingala (Pingala) ( fl. 300-200 aC), un teórico musical que fue autor de la Chandas Shastra (chandaḥ-śāstra, también Chandas Sutra chandaḥ-sutra), una sánscrito tratado sobre prosodia. Hay pruebas de que en su obra sobre la enumeración de las combinaciones silábicas, Pingala tropezado tanto el triángulo de Pascal y coeficientes binomiales , aunque él no tenía conocimiento de la Sí teorema binomial. La obra de Pingala también contiene las ideas básicas de los números de Fibonacci (llamado maatraameru). Aunque el sutra Chandah no se ha conservado en su totalidad, un comentario siglo 10 en él por Halayudha tiene. Halayudha, que se refiere al triángulo de Pascal como Meru-prastāra (literalmente "la escalera Monte Meru "), tiene esto que decir:

"Dibuja un cuadrado A partir de la mitad de la plaza, dibujar otras dos plazas similares por debajo de ella;. Por debajo de estos dos, tres otras plazas, etc. El marcado debe iniciarse poniendo 1 en la primera plaza Ponga 1 en cada uno de los.. dos plazas de la segunda línea. En la tercera línea ponen 1 en los dos cuadrados en los extremos y, en la plaza central, la suma de los dígitos en las dos plazas situadas por encima de ella. En la cuarta línea ponen 1 en los dos cuadrados en los extremos. En los medios poner la suma de los dígitos en las dos plazas por encima de cada uno. Proceder de esta manera. De estas líneas, la segunda proporciona las combinaciones con una sílaba, la tercera las combinaciones con dos sílabas, ... "

El texto también indica que Pingala era consciente de la combinatoria de identidad:

${N \ choose 0} + {n \ choose 1} + {n \ choose 2} + \ cdots + {n \ eligen n-1} + {n \ choose n} = 2 ^ n$

Katyayana

Aunque no es un matemático de Jaina, Katyayana (c. 3 ª siglo aC) se caracteriza por ser el último de los matemáticos védicos. Él escribió el Katyayana Sulba Sutra, que presentó mucho geometría , incluyendo al general teorema de Pitágoras y un cálculo de la raíz cuadrada de 2 correcta a cinco decimales.

La tradición escrita: Comentario Prosa

Con la creciente complejidad de las matemáticas y otras ciencias exactas, se exigió a la escritura y cálculo. En consecuencia, muchos trabajos matemáticos comenzaron a ser escritas en manuscritos que luego fueron copiados y re-copiados de generación en generación.

"Se estima la India de hoy a tener cerca de treinta millones de manuscritos, la mayor masa de material de lectura, escrita a mano en cualquier parte del mundo. La cultura letrada de la ciencia de la India se remonta a por lo menos el siglo V antes de Cristo ... como se muestra por los elementos de la Mesopotamia literatura augurio y la astronomía que entró en la India en ese momento y (eran) definitivamente no ... preservados oralmente ".

El primer matemático prosa comentario era que en el trabajo, Aryabhatiya (escrito 499 CE), un trabajo sobre astronomía y matemáticas. La parte matemática del Aryabhatiya se compone de 33 sutras (en forma de verso) que consisten en declaraciones o reglas matemáticas, pero sin ningún tipo de pruebas. Sin embargo, de acuerdo con (Hayashi 2003, p. 123), "esto no necesariamente significa que sus autores no probaron ellos. Fue probablemente una cuestión de estilo de la exposición." Desde el momento de Bhaskara I (600 CE en adelante), comentarios en prosa cada vez empecé a incluir algunas derivaciones (upapatti). El comentario de Bhaskara I en el Aryabhatiya, tenía la siguiente estructura:

Regla ('sutra') en el versículo por Aryabhata
Comentario por Bhaskara I, que consiste en:
- La aclaración de reglas (derivaciones eran aún poco frecuente entonces, pero se hizo más común después)
- Ejemplo (uddeśaka) generalmente en verso.
- Configuración (nyāsa / sthapana) de los datos numéricos.
- Trabajo (karana) de la solución.
- Verificación (pratyayakaraṇa, literalmente "hacer convicción") de la respuesta. Estos se convirtieron en raras En el siglo 13, derivaciones o pruebas siendo favorecido por entonces.

Por lo general, para cualquier tema matemático, los estudiantes en la India antigua primero memorizan los sutras, que, como se explicó anteriormente, eran "deliberadamente inadecuada" en los detalles explicativos (con el fin de transmitir sucintamente las reglas matemáticas desnudo-huesos). Luego, los estudiantes trabajaron a través de los temas de los comentarios en prosa de la escritura (y dibujar diagramas) en polvo de creta y tableros (es decir, tableros cubiertos de polvo). Esta última actividad, un elemento básico de trabajo matemático, fue más tarde símbolo matemático-astrónomo, Brahmagupta ( fl. CE del siglo séptimo), para caracterizar los cálculos astronómicos como "trabajo de polvo" (en sánscrito: dhulikarman).

Los números y el sistema numérico decimal

La más antigua existente escritura usada en la India fue el Guión Kharoṣṭhī utiliza en el Cultura Gandhara del noroeste. Se piensa que es de Origen arameo y fue en uso desde el siglo IV aC al siglo IV. Casi simultáneamente, otro script, el Brahmi, apareció en gran parte del subcontinente, y más tarde se convertiría en la base de muchos guiones de Asia meridional y Asia sudoriental. Ambos guiones tenían símbolos numéricos y sistemas de numeración, que inicialmente no estaban basadas en un sistema de valor. La primera evidencia fechable del uso del sistema decimal de posición-valor en la India se encuentra en el Yavanajātaka ( ca. 270 CE) de Sphujidhvaja, una versificación de una anterior (ca. 150 dC) la adaptación prosa indio de una obra perdida de la astrología helenística.

Bakhshali Manuscrito

El manuscrito matemático más antiguo existente en el sur de Asia es la Bakhshali Manuscrito, un manuscrito escrito en corteza de abedul "híbrido budista sánscrito" en el guión Sarada, que fue utilizado en la región noroeste del subcontinente indio entre los siglos 12 y 8 de la CE. El manuscrito fue descubierto en 1881 por un agricultor mientras cavaba en un recinto de piedra en el pueblo de Bakhshali, cerca Peshawar (entonces en India británica y ahora en Pakistán ). De autor desconocido y ahora se conserva en el Biblioteca Bodleian de la Universidad de Oxford , el manuscrito ha sido fechado -como diversamente pronto como los "primeros siglos de la era cristiana" y tan tarde como entre el 9 y el CE del siglo 12. El CE del siglo séptimo se considera ahora una fecha creíble, aunque con la posibilidad de que el "manuscrito en su forma actual constituye un comentario o una copia de un trabajo matemático anterior."

El manuscrito sobrevivir tiene setenta hojas, algunas de las cuales están en fragmentos. Su contenido matemático consiste en reglas y ejemplos, escritas en verso, junto con comentarios en prosa, que incluyen soluciones a los ejemplos. Los temas tratados incluyen aritméticas (fracciones, raíces cuadradas, ganancias y pérdidas, el interés simple, los regla de tres, y regula falsi) y álgebra (simultánea ecuaciones lineales y ecuaciones de segundo grado ), y progresiones aritméticas. Además, hay un puñado de problemas geométricos (incluyendo problemas sobre volúmenes de sólidos irregulares). El manuscrito Bakhshali también "emplea un sistema de valores decimales con un punto de cero." Muchos de sus problemas son los llamados problemas de ecualización que conducen a sistemas de ecuaciones lineales. Un ejemplo de fragmento III-5-3v es la siguiente:

"Un comerciante tiene siete caballos asava, una segunda cuenta con nueve caballos haya, y un tercero tiene diez camellos. Son igual de bien fuera en el valor de sus animales si cada uno da dos animales, uno para cada uno de los otros. Encuentra el precio de cada animal y el valor total de los animales que posee cada comerciante ".

El comentario que acompaña a la prosa ejemplo resuelve el problema mediante la conversión a tres (bajo-determinado) ecuaciones en cuatro incógnitas y suponiendo que los precios son todos los enteros.

Periodo Clásico (400 - 1200)

Este período es a menudo conocido como la edad de oro de la Matemática de la India. Este período vio matemáticos como Aryabhata, Varahamihira, Brahmagupta, Bhaskara I, Mahavira, y Bhaskara II dan forma más amplia y más clara a muchas ramas de las matemáticas. Sus contribuciones se extendería a Asia , el Oriente Medio , y eventualmente a Europa . A diferencia de las matemáticas védicas, sus trabajos incluyen tanto las contribuciones astronómicos y matemáticos. De hecho, las matemáticas de la época fue incluido en la "ciencia astral" (jyotiḥśāstra) y consistieron en tres sub-disciplinas: ciencias matemáticas (Ganita o tantra), la astrología horóscopo (Hora o jātaka) y la adivinación (Samhita). Esta división tripartita se ve en Sexto siglo de Varahamihira Pancasiddhantika compilation- (literalmente panca, "cinco", siddhānta, "conclusión de la deliberación", de fecha 575 CE) -de cinco obras anteriores, Surya Siddhanta, Romaka Siddhanta, Paulisa Siddhanta, Vasishtha Siddhanta y Paitamaha Siddhanta, que eran adaptaciones de obras aún anteriores de la astronomía mesopotámica, griega, egipcia, romana y de la India. Como se explicó anteriormente, los principales textos fueron compuestos en sánscrito verso, y fueron seguidos por los comentarios en prosa.

Siglos V y VI

Surya Siddhanta

Aunque su autoría es desconocida, la Surya Siddhanta (c. 400) contiene las raíces del moderno trigonometría . Algunos autores consideran que su fue escrito bajo la influencia de Mesopotamia y Grecia. Sin embargo, según Flavio Filostratus registra Pitágoras en el siglo quinto antes de Cristo y Apolonio de Tiana en el siglo 1 CE fue a estudiar en India.Furthermore no hay pruebas contundentes para demostrar que los matemáticos griegos tuvieron fuerte influencia en la astronomía griega.

Este antiguo texto utiliza la siguiente como funciones trigonométricas, por primera vez:

Sine (Jya).
Coseno (Kojya).
Seno inverso (Otkram jya).

También contiene los primeros usos de:

Tangente .
Secante.

Los ciclos de tiempo cosmológicas hindúes explican en el texto, que fue copiado de un trabajo anterior, da:
- La duración media de la año sideral como 365.2563627 días, que es sólo 1,4 segundos más que el valor moderno de 365,2563627 día.
- La duración media de la año tropical como 365.2421756 días, que son sólo 2 segundos más corto que el valor moderno de 365,2421988 día.

Más tarde los matemáticos indios como Aryabhata hace referencia a este texto, mientras que más tarde árabes y latinos traducciones fueron muy influyentes en Europa y el Medio Oriente.

Calendario Chhedi

Este calendario Chhedi (594) contiene un uso temprano de lo moderno lugar-valor Sistema de numeración utilizado ahora universalmente Hindú-Árabe (véase también Numerales indo-arábigos).

Aryabhata I

Aryabhata (476-550) escribió el Aryabhatiya. Describió los principios fundamentales importantes de las matemáticas en el 332 shlokas. El tratado contenía:

Ecuaciones cuadráticas
Trigonometría
El valor de π , corregir a 4 decimales.

Aryabhata también escribió el Arya Siddhanta, que se ha perdido. Las contribuciones de Aryabhata incluyen:

Trigonometría:

Introducido las funciones trigonométricas .
Definido el seno (jya) como la relación moderna entre medio un ángulo y la mitad de un acorde.
Definido el coseno (kojya).
Definido el versine (ukramajya).
Definido el seno inverso (otkram jya).
Métodos de cálculo de los valores numéricos aproximados Gave.
Contiene las primeras tablas de valores de seno, coseno y versine, en 3.75 ° intervalos de 0 ° a 90 °, a 4 decimales de precisión.
Contiene el pecado trigonométrica fórmula (n + 1) x - sen nx = nx pecado - el pecado (n - 1) x - (1/225) nx pecado.
Trigonometría esférica.

Aritmética:

Fracciones continuas.

Algebra:

Las soluciones de ecuaciones cuadráticas simultáneas.
Soluciones con números enteros de ecuaciones lineales por un método equivalente al método moderno.
Solución general de la ecuación lineal indeterminado.

Astronomía matemática:

Propuesto por primera vez, un heliocéntrica del sistema solar con los planetas girando sobre su ejes y tras una elíptica órbita alrededor del Sol
Cálculos precisos para las constantes astronómicas, como el:
- Eclipse solar .
- Eclipse lunar .
- La fórmula para la suma de la cubos, lo cual fue un paso importante en el desarrollo del cálculo integral.

Cálculo:

Infinitesimales:
- En el curso del desarrollo de un inventario detallado del eclipse lunar, Aryabhatta se vio obligado a introducir el concepto de los infinitesimales (tatkalika gati) para designar el movimiento instantáneo cerca de la luna.
Ecuaciones diferenciales :
- Expresó el movimiento casi instantánea de la luna en la forma de una ecuación diferencial básica.
Función exponencial:
- Usó lafunción exponencial een su ecuación diferencial del movimiento instantáneo cerca de la luna.

Varahamihira

Varahamihira (505-587) produjo el Pancha Siddhanta ( Los Cinco astronómicos Cánones ). Hizo importantes contribuciones a la trigonometría , incluyendo seno y coseno tablas a 4 decimales de precisión y las siguientes fórmulas relativas seno y coseno funciones:

$\sin^2(x) + \cos^2(x) = 1$

$\sin(x)=\cos\left(\frac{\pi}{2}-x\right)$

$\frac{1-\cos(2x)}{2}=\sin^2(x)$

Siglos VII y VIII

El teorema de Brahmagupta afirma queAF=FD.

En el siglo VII, dos campos separados, la aritmética (que incluía medición ) y el álgebra , comenzó a surgir en las matemáticas indias. Los dos campos más tarde serían llamados Pati-Ganita (literalmente "las matemáticas de los algoritmos") y bīja-Ganita (lit. "matemáticas de semillas", con "semillas" -como las semillas de las plantas-que representan incógnitas con el potencial de generar, en este caso, las soluciones de ecuaciones). Brahmagupta, en su obra astronómica Brāhma Sphuta Siddhānta (628 CE), incluidos dos capítulos (12 y 18) dedicadas a estos campos. Capítulo 12, que contiene 66 versos sánscritos, se divide en dos secciones: "Operaciones básicas" (incluyendo raíces cúbicas, fracciones, razón y proporción, y de trueque) y "matemáticas prácticos" (incluyendo mezcla, series matemáticas, figuras planas, ladrillos de apilamiento, aserrado de la madera, y apilamiento de grano). En este último apartado, declaró su famoso teorema sobre las diagonales de un cuadrilátero cíclico:

Teorema de Brahmagupta:Si uncuadrilátero cíclico tiene diagonales que sonperpendiculares entre sí, entonces la línea perpendicular trazada desde el punto de intersección de las diagonales a cualquier lado del cuadrilátero siempre biseca el lado opuesto.

Capítulo 12 también incluye una fórmula para el área de un cuadrilátero cíclico (una generalización dela fórmula de Heron), así como una descripción completa detriángulos racionales (es decir,triángulos con los lados racionales y áreas racional).

La fórmula de Brahmagupta:El área,A, de uncuadrilátero cíclico con lados de longitudes deun,b,c,d, respectivamente, está dada por

$A = \sqrt{(s-a)(s-b)(s-c)(s-d)}$

dondes, elsemiperímetro, dada por: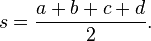 $s=\frac{a+b+c+d}{2}.$

Teorema de Brahmagupta en triángulos racionales:Un triángulo con lados racionales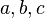 $a, b, c$ y zona racional es de la forma:

$a = \frac{u^2}{v}+v, \ \ b=\frac{u^2}{w}+w, \ \ c=\frac{u^2}{v}+\frac{u^2}{w} - (v+w)$

para algunos números racionales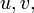 $u, v,$ y $w$ .

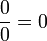Capítulo 18 contiene 103 versos sánscritos que comenzaron con las normas para las operaciones aritméticas con números cero y negativos y se considera el primer tratamiento sistemático del tema. Las normas (que incluyó $a + 0 = \ a$ y $a \times 0 = 0$ ) eran los correctos, con una excepción: $\frac{0}{0} = 0$ . Más adelante en el capítulo, dio la primera solución explícita (aunque todavía no del todo general) de la ecuación de segundo grado :

$\ ax^2+bx=c$

Para el número absoluto multiplicado por cuatro veces el [coeficiente de la] cuadrado, añadir el cuadrado de la [coeficiente del] medio plazo; la raíz cuadrada de la misma, menos el [coeficiente de la] término medio, se divide en dos veces el [coeficiente de la] plaza es el valor. ( Brahmasphutasiddhanta (traducción Colebrook, 1817, página 346)

Esto es equivalente a:

$x = \frac{\sqrt{4ac+b^2}-b}{2a}$

También en el capítulo 18, Brahmagupta fue capaz de avanzar en la búsqueda de soluciones integrales () de la ecuación de Pell,

$\ x^2-Ny^2=1,$

donde $N$ es un número entero no cuadrado. Lo hizo mediante el descubrimiento de la siguiente identidad:

Identidad de Brahmagupta: $\ (x^2-Ny^2)(x'^2-Ny'^2) = (xx'+Nyy')^2 - N(xy'+x'y)^2$ que era una generalización de una identidad anterior deDiofanto: Brahmagupta usó su identidad para probar el siguiente lema:

Lema (Brahmagupta):Si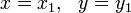 $x=x_1,\ \ y=y_1 \ \$ es una solución de $\ \ x^2 - Ny^2 = k_1,$ y, $x=x_2, \ \ y=y_2 \ \$ una solución de $\ \ x^2 - Ny^2 = k_2,$ , entonces:

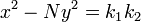
$x=x_1x_2+Ny_1y_2,\ \ y=x_1y_2+x_2y_1 \ \$ es una solución de $\ x^2-Ny^2=k_1k_2$

Luego utilizó este lema tanto a generar un número infinito de soluciones (integrales) de la ecuación de Pell, dada una solución, e indicar el siguiente teorema:

Teorema (Brahmagupta):Si la ecuación $\ x^2 - Ny^2 =k$ tiene una solución entera para cualquiera de $\ k=\pm 4, \pm 2, -1$ entonces la ecuación de Pell:

$\ x^2 -Ny^2 = 1$

también tiene una solución entera.

Brahmagupta en realidad no probar el teorema, sino que funcionó ejemplos usando su método. El primer ejemplo que presentó fue:

Ejemplo (Brahmagupta):Encuentra los números enteros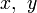 $\ x,\ y\$ tal que:

$\ x^2 - 92y^2=1$

En su comentario, Brahmagupta añadió, "una persona la solución de este problema dentro de un año es un matemático". La solución que proporcionó fue:

$\ x=1151, \ y=120$

Bhaskara I

Bhaskara I (c. 600-680) amplié el trabajo de Aryabhata en sus libros titulados Mahabhaskariya , Aryabhattiya Bhashya y Laghu Bhaskariya . Produjo:

Soluciones de ecuaciones indeterminadas.
Una aproximación racional de lafunción seno.
Una fórmula para el cálculo del seno de un ángulo agudo sin el uso de una mesa, corregir a 2 cifras decimales.

Novena a la duodécima siglos

Virasena

Virasena (siglo 9) fue un matemático Jaina en la corte del rey Rashtrakuta Amoghavarsha de Manyakheta, Karnataka. Él escribió el Dhavala , un comentario sobre las matemáticas jainistas, que:

Se ocupa de los logaritmos de base 2 (ardhaccheda) y describe sus leyes.
Primero usa logaritmos basar 3 (trakacheda) y la base 4 (caturthacheda).

Virasena también dio:

La derivación de lavolumende uncono truncado por una especie de procedimiento infinito.

Mahavira

Mahavira Acharya (c. 800-870) de Karnataka, el último de los notables matemáticos Jaina, vivió en el siglo noveno y fue patrocinado por el rey Rashtrakuta Amoghavarsha. Escribió un libro titulado Ganit Saar Sangraha en las matemáticas numéricas, y también escribió tratados sobre una amplia gama de temas matemáticos. Estos incluyen las matemáticas de:

Cero.
Cuadrados.
Cubos.
raíces cuadradas,raíces cúbicas, y lasseries que se extienden más allá de éstos.
Geometría plana.
Geometría sólida.
Los problemas relacionados con la fundición desombras.
Fórmulas deriva para calcular el área de unaelipseycuadrilátero dentro de uncírculo

Mahavira también:

Afirmó que laraíz cuadradade unnúmero negativono existía
Dio la suma de unaserie cuyos términos soncuadrados de unaprogresión aritmética, y dio reglas empíricas parael áreayperímetro de unaelipse.
Ecuaciones cúbicas resuelto.
Ecuaciones cuárticas resuelto.
Resuelto algunasecuaciones de quinto grado y de orden superiorpolinomios.
Dio las soluciones generales de las ecuaciones polinómicas de orden superior:
- $\ ax^n = q$
- $a \frac{x^n - 1}{x - 1} = p$
Resuelto ecuaciones cuadráticas indeterminadas.
Resuelto ecuaciones cúbicas indeterminadas.
Resuelto ecuaciones de orden superior indeterminadas.

Shridhara

Shridhara (c. 870-930), que vivió en Bengala, escribió los libros titulados Nav Shatika , Tri Shatika y Pati Ganita . El dio:

Una buena regla para encontrar elvolumende unaesfera.
La fórmula para resolverecuaciones de segundo grado.

El Pati Ganita es una obra en la aritmética y la medición . Se trata de diversas operaciones, incluyendo:

Operaciones elementales
La extracción de raíces cuadradas y cúbicas.
Fracciones.
Ocho reglas dadas para las operaciones en cero.
Métodos desuma de diferentes series aritméticas y geométricas, que se convirtiera en referencias estándar en obras posteriores.

Manjula

Ecuaciones diferenciales de Aryabhata se elaboraron en el siglo 10 por Manjula (tambiénMunjala), quien se dio cuenta de que la expresión

$\ \sin w' - \sin w$

podría expresarse aproximadamente como

$\ (w' - w)\cos w$

Él entendió el concepto de diferenciación después de resolver la ecuación diferencial resultante de la sustitución de esta expresión en la ecuación diferencial de Aryabhata.

Aryabhata II

Aryabhata II (c. 920-1000) escribió un comentario sobre Shridhara, y un tratado astronómico Maha-Siddhanta . El Maha-Siddhanta tiene 18 capítulos, y discute:

Matemáticas numéricas (Ank Ganit).
Álgebra.
Soluciones de ecuaciones indeterminadas (kuttaka).

Shripati

Shripati Mishra (1019-1066) escribió los libros Siddhanta Shekhara , una obra importante en la astronomía en 19 capítulos, y Ganit tilaka , un incompleto aritmética tratadistas en 125 versos basados en una obra de Shridhara. Trabajó principalmente en:

Permutaciones y combinaciones.
Solución general de la ecuación lineal indeterminado simultánea.

También fue el autor deDhikotidakarana, una obra de veinte versos sobre:

ElDhruvamanasaes una obra de 105 versículos sobre:

Cálculo planetarioslongitudes
eclipses.
planetario tránsitos.

Nemichandra Siddhanta Chakravati

Nemichandra Siddhanta Chakravati (c. 1100) fue autor de un tratado matemático tituladoGome-mat Saar.

Bhaskara II

Bhāskara II (1114-1185) fue un matemático-astrónomo que escribió varios tratados importantes, a saber, el Siddhanta Shiromani , Lilavati , Bijaganita , Gola Addhaya , Griha Ganitam y Karan Kautoohal . Un número de sus contribuciones se transmite después a Oriente Medio y Europa. Sus contribuciones incluyen:

Aritmética:

Cómputo interés.
Progresiones aritméticas y geométricas.
Geometría plana.
Geometría sólida.
La sombra de la gnomon.
Soluciones de combinaciones.
Dio una prueba de la división porceroserinfinito.

Algebra:

El reconocimiento de un número positivo tiene dos raíces cuadradas.
Irracionales.
Operaciones con productos de varias incógnitas.
Las soluciones de:
- Ecuaciones cuadráticas.
- Ecuaciones cúbicas.
- Ecuaciones de cuarto grado.
- Ecuaciones con más de un desconocido.
- Ecuaciones cuadráticas con más de un desconocido.
- La forma general dela ecuación de Pell usando el chakravalamétodo.
- La ecuación cuadrática indeterminada general utilizando elchakravalamétodo.
- Ecuaciones cúbicas indeterminados.
- Ecuaciones cuárticas indeterminados.
- De orden superior indeterminadospolinomiosecuaciones.

Geometría:

Dio una prueba delteorema de Pitágoras.

Cálculo:

Concebida cálculo diferencial.
Descubierto elderivado.
Descubierto elcoeficiente diferencial.
Desarrollado diferenciación.
Dichoteorema de Rolle, un caso especial de lateorema del valor medio (uno de los teoremas más importantes de cálculo y análisis).
Derivado el diferencial de la función seno.
Computarizadaπ, corregir a 5 decimales.
Calculado de la longitud de la revolución de la Tierra alrededor del Sol a 9 cifras decimales.

Trigonometría:

La evolución dela trigonometría esférica
Las fórmulas trigonométricas:
- $\ \sin(a+b)=\sin(a) \cos(b) + \sin(b) \cos(a)$
- $\ \sin(a-b)=\sin(a) \cos(b) - \sin(b) \cos(a)$

Kerala Matemáticas (1300 - 1600)

La Escuela de Kerala de la astronomía y las matemáticas fue fundada por Madhava de Sangamagrama en Kerala , sur de la India y la incluyó entre sus miembros: Parameshvara, Neelakanta Somayaji, Jyeshtadeva, Achyuta Pisharati, Melpathur Narayana Bhattathiri y Achyuta Panikkar. Floreció entre los 14o y 16o siglos y los descubrimientos originales de la escuela parece haber terminado con Narayana Bhattathiri ( 1559- 1632). En un intento de resolver los problemas astronómicos, los astrónomos de la escuela de Kerala independiente creado una serie de importantes conceptos matemáticos. Los resultados más importantes, desarrollo en serie de funciones trigonométricas , se les dio en sánscrito verso en un libro de Neelakanta llama Tantrasangraha y un comentario sobre esta obra llamados Tantrasangraha-vakhya de autor desconocido. Los teoremas se declararon sin pruebas, pero pruebas de la serie de seno , coseno , y inversa tangente se proporcionaron un siglo más tarde en el trabajo Yuktibhasa (c.1500-c.1610), escrito en malayalam, por Jyesthadeva, y también en un comentario sobre Tantrasangraha .

Su descubrimiento de estos tres desarrollos en serie importantes de cálculo siglos -varios antes cálculo fue desarrollado en Europa por Isaac Newton y Gottfried Leibniz -era un logro histórico en matemáticas. Sin embargo, la Escuela de Kerala no se puede decir que inventó el cálculo , ya que, mientras ellos fueron capaces de desarrollar desarrollos en serie de Taylor para las funciones trigonométricas importantes, desarrollaron ni una teoría completa de la diferenciación o integración , ni el teorema fundamental del cálculo . Los resultados obtenidos por la escuela Kerala incluyen:

El (infinita)serie geométrica: 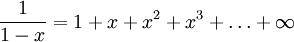$\frac{1}{1-x} = 1 + x + x^2 + x^3 + \dots + \infty$ para $|x|<1$ Esta fórmula ya se sabe, por ejemplo, en la obra del matemático árabe del siglo décimoAlhazen (la forma latinizada del nombre de Ibn al-Haytham (965-1039)).
Una prueba semi-rigurosa (ver "inducción" observación a continuación) del resultado: 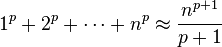$1^p+ 2^p + \cdots + n^p \approx \frac{n^{p+1}}{p+1}$ para grandes n . Este resultado también era conocido por Alhazen.
Uso intuitivo deinducción matemática, sin embargo, la hipótesis de inducciónfue formulado o no emplea en pruebas.
Las aplicaciones de las ideas de (lo que se convertiría) diferencial e integralde cálculopara obtener(Taylor-Maclaurin) serie infinitade $\sin x$ , $\cos x$ Y $\arctan x$ ElTantrasangraha-vakhyada la serie en verso, que cuando se traducen a la notación matemática, se puede escribir como:

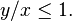
$r\arctan(\frac{y}{x}) = \frac{1}{1}\cdot\frac{ry}{x} -\frac{1}{3}\cdot\frac{ry^3}{x^3} + \frac{1}{5}\cdot\frac{ry^5}{x^5} - \cdots ,$ donde $y/x \leq 1.$

$\sin x = x - x\cdot\frac{x^2}{(2^2+2)r^2} + x\cdot \frac{x^2}{(2^2+2)r^2}\cdot\frac{x^2}{(4^2+4)r^2} - \cdot$

$r - \cos x = r\cdot \frac{x^2}{(2^2-2)r^2} - r\cdot \frac{x^2}{(2^2-2)r^2}\cdot \frac{x^2}{(4^2-4)r^2} + \cdots ,$ donde, por $r = 1$ , la serie de reducir a la serie de potencias estándar para estas funciones trigonométricas, por ejemplo:

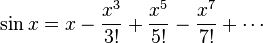- $\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots$ y
- $\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots$
El uso de rectificación (cálculo de longitud) del arco de un círculo para dar una prueba de estos resultados. (El método más tarde de Leibniz, utilizando cuadratura ( es decir, el cálculo de área bajo el arco del círculo, se no utiliza.)
El uso de expansión de la serie de $\arctan x$ la obtención de una expresión serie infinita (más tarde conocido como serie Gregory) para $\ Pi$ :

$\frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \ldots + \infty$

Una aproximación racional de error para la suma finita de su serie de interés. Por ejemplo, el error, $f_i(n+1)$ , (para n impar, y i = 1, 2, 3 ) para la serie:

$\frac{\pi}{4} \approx 1 - \frac{1}{3}+ \frac{1}{5} - \cdots (-1)^{(n-1)/2}\frac{1}{n} + (-1)^{(n+1)/2}f_i(n+1)$

donde $f_1(n) = \frac{1}{2n}, \ f_2(n) = \frac{n/2}{n^2+1}, \ f_3(n) = \frac{(n/2)^2+1}{(n^2+5)n/2}.$

La manipulación del término de error para derivar una serie de convergencia más rápida para $\ Pi$ :

$\frac{\pi}{4} = \frac{3}{4} + \frac{1}{3^3-3} - \frac{1}{5^3-5} + \frac{1}{7^3-7} - \cdots \infty$

Utilizando la serie mejorada para derivar una expresión racional, 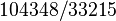$104348/33215$ para $\ Pi$ corregir hastanuevecifras decimales,es decir, $3.141592653$
El uso de una noción intuitiva de límite para calcular los resultados.
Un semi-rigurosa (ver observación sobre los límites arriba) método de diferenciación de algunas funciones trigonométricas. Sin embargo, ellos no formular la noción de una función , o tener conocimientos de las funciones exponenciales o logarítmicas.

Las obras de la escuela de Kerala fueron escritas por primera vez para el mundo occidental por el inglés CM Whish en 1835 . Según Whish, los matemáticos Kerala tenían " sentó las bases para un sistema completo de fluxiones "y estas obras abundó" con formas fluxionales y series que se encuentran en ninguna obra de países extranjeros. " Sin embargo, los resultados de Whish fueron casi completamente descuidados, hasta más de un siglo más tarde, cuando los descubrimientos de la escuela de Kerala fueron investigados nuevamente por C. Rajagopal y sus asociados. Su trabajo incluye comentarios sobre las pruebas de la serie arctan en Yuktibhasa dada en dos artículos, un comentario sobre la Yuktibhasa ' s prueba de la serie de seno y el coseno y dos documentos que proporcionan los sánscritos versos del Tantrasangrahavakhya para la serie de arctan, el pecado , y el coseno (con traducción al Inglés y comentario).

Los matemáticos de Kerala incluyen Narayana Pandit (c. 1340-1400), quien compuso dos obras, un tratado de aritmética, Ganita Kaumudi , y un tratado algebraica, Bijganita Vatamsa . Narayana también se piensa que es el autor de un comentario detallado de de Bhaskara II Lilavati, titulado Karmapradipika (o Karma-Paddhati ). Madhava de Sangamagramma (. c 1340-1425) fue el fundador de la Escuela de Kerala. Aunque es posible que escribió Karana Paddhati un trabajo escrito en algún momento entre 1375 y 1475, todo lo que realmente sabemos de su trabajo proviene de obras de estudiosos posteriores.

Parameshvara (. C 1370-1460) escribió comentarios sobre las obras de Bhaskara I, Aryabhata y Bhaskara II. Su Lilavati Bhasya , un comentario sobre de Bhaskara II Lilavati , contiene uno de sus importantes descubrimientos: una versión de la teorema del valor medio. Nilakantha Somayaji (1444-1544) compuso el Tantra Samgraha (que ' generado "un comentario anónimo tarde Tantrasangraha-vyākhyā y un comentario más por el nombre Yuktidipaika , escrito en 1501). Elaboró y extendió las contribuciones de Madhava.

Citrabhanu (c. 1530) fue un matemático del siglo 16 de Kerala que dio soluciones enteras a 21 tipos de sistemas de dos ecuaciones algebraicas simultáneas con dos incógnitas. Estos tipos son todos los posibles pares de ecuaciones de las siguientes siete formas:

$\ x + y = a, x - y = b, xy = c, x^2 + y^2 = d, x^2 - y^2 = e, x^3 + y^3 = f, x^3 - y^3 = g$

Para cada caso, Citrabhanu dio una explicación y justificación de su gobierno, así como un ejemplo. Algunos de sus explicaciones son algebraica, mientras que otros son geométricos. Jyesthadeva (c. 1500-1575) fue otro miembro de la Escuela de Kerala. Su obra clave fue la Yukti-Bhasa (escrito en malayalam, una lengua regional de Kerala ). Jyesthadeva presentó pruebas de la mayoría de los teoremas matemáticos y series infinitas anteriormente descubiertos por Madhava y otros matemáticos Escuela Kerala.

Cargos de eurocentrismo

Se ha sugerido que las contribuciones a las matemáticas indias no han recibido el debido reconocimiento en la historia moderna y que muchos descubrimientos e invenciones de los matemáticos indios están actualmente culturalmente atribuidos a sus homólogos occidentales, como resultado del eurocentrismo. Según GG Joseph:

[Su trabajo] lleva a bordo algunas de las objeciones planteadas acerca de la trayectoria eurocéntrica clásica. La conciencia [de la matemática india y árabe] es muy probable que sea templado con rechazos desdeñosas de su importancia en comparación con las matemáticas griegas. Las contribuciones de otras civilizaciones - especialmente China e India, se perciben ya sea como prestatarios de fuentes griegas o habiendo hecho sólo contribuciones menores a incorporar el desarrollo matemático. Una apertura a las conclusiones de las investigaciones más recientes, especialmente en el caso de las matemáticas indias y chinas, es tristemente desaparecida "

El historiador de las matemáticas,Florian Cajori, sugirió que "sospechan [s] queDiofanto consiguió su primera visión del conocimiento algebraico de la India. "

Más recientemente, como se discutió en la sección anterior, la serie infinita de cálculo para las funciones trigonométricas (redescubierto por Gregory, Taylor y de Maclaurin a finales del siglo 17) se describe (con pruebas) en la India, por los matemáticos de la Escuela de Kerala, notablemente unos dos siglos antes. Algunos estudiosos han sugerido recientemente que el conocimiento de estos resultados podría haber sido transmitido a Europa a través de la ruta comercial de Kerala por los comerciantes y misioneros jesuitas. Kerala estaba en contacto continuo con China, y Arabia, y, a partir de alrededor de 1500, con Europa. La existencia de vías de comunicación y una cronología adecuada sin duda realizar una transmisión de tal posibilidad. Sin embargo, no hay evidencia directa a título de manuscritos relevantes que tal transmisión tuvo lugar realmente. De hecho, de acuerdo con David Bressoud, "no hay evidencia de que el trabajo de la India de la serie era conocida más allá de la India, o incluso fuera de Kerala, hasta el siglo XIX."

Ambos estudiosos árabes e indios hicieron descubrimientos antes de que el siglo 17 que ahora se considera una parte de cálculo. Sin embargo, no pudieron, como Newton y Leibniz eran, "combinar muchas ideas diferentes en los dos temas unificadores de la derivada y la integral , mostrar la conexión entre los dos, y gire el cálculo en la gran herramienta de resolución de problemas que tienen hoy ". Las carreras intelectuales tanto de Newton y Leibniz están bien documentados y no hay ninguna indicación de que su trabajo no ser su propio; sin embargo, no se sabe con certeza si los inmediatos predecesores de Newton y Leibniz, "incluyendo, en particular, Fermat y Roberval, aprendido de algunas de las ideas de los matemáticos islámicos e indios a través de fuentes que no son conscientes." Esta es un área activa de investigación actual, sobre todo en las colecciones de manuscritos de España y el Magreb , la investigación que ahora se persigue, entre otros lugares, en el Centro Nacional de Investigación Científica de París .

Recuperado de " http://en.wikipedia.org/w/index.php?title=Indian_mathematics&oldid=197000390 "

Home Page - YouTube Channel