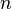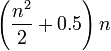Quadrado mágico
Informações de fundo
Crianças SOS têm produzido uma seleção de artigos da Wikipédia para escolas desde 2005. Você quer saber sobre o patrocínio? Veja www.sponsorachild.org.uk
Em matemática recreativa, um quadrado mágico de ordem n é um arranjo de números n ², geralmente distintas inteiros , em uma praça , de modo que os números n em todas as linhas, todas as colunas, e ambas as diagonais somar a mesma constante. Um quadrado mágico normal contém os inteiros de 1 a n ². O termo "quadrado mágico" também é por vezes utilizado para se referir a qualquer um dos vários tipos de praça palavra.
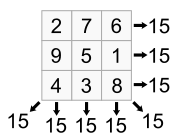
Existem quadrados mágicos normais para todas as encomendas n ≥ 1, com excepção n = 2, embora o caso n = 1 é trivial-lo é composto por uma única célula que contém o número 1. O menor caso não trivial, mostrada abaixo, é de ordem 3.
A soma constante em cada linha, coluna e diagonal é chamado de constante mágica ou soma mágica, M. A constante mágica de um quadrado mágico normal, depende apenas de n e tem o valor
Para quadrados mágicos normais de ordem n = 3, 4, 5, ..., as constantes mágicas são:
- 15, 34, 65, 111, 175, 260, ... (sequência A006003 em OEIS ).
História de quadrados mágicos
O quadrado Lo Shu (3 × 3 quadrado mágico)
Chinês literatura datado de tão cedo quanto 650 aC conta a lenda de Lo Shu ou "rolagem do rio Lo". Na China antiga , havia uma enorme inundação. As pessoas tentaram oferecer algum sacrifício ao deus do rio de um dos rios inundações, o rio Lo, para acalmar sua raiva. Então, surgiu a partir da água uma tartaruga com uma figura / padrão curioso em seu escudo; houve pontos circulares de números que foram dispostas em um padrão de três por três de nove grelha de tal modo que a soma dos números em cada fila, coluna e diagonal foi o mesmo: 15. Este número também é igual ao número de dias em cada dos 24 ciclos do Ano solar chinês. Este padrão, de uma certa maneira, foi usada pelo povo no controle do rio.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
O Lo Shu Square, como o quadrado mágico sobre a carapaça de tartaruga é chamado, é o quadrado mágico normais única de ordem três, em que 1 é na parte inferior e 2 está no canto superior direito. Cada quadrado mágico normal da ordem de três é obtido a partir da Lo Shu por rotação ou reflexão.
A Praça de Lo Shu também é referido como o quadrado mágico de Saturno ou Cronos. Seu valor numérico é obtido a partir do funcionamento do I Ching quando o Trigramas são colocados numa ordem dada no primeiro mapa rio, o Ho Tu ou rio Amarelo . O Ho Tu produz 4 quadrados de Hexagramas 8 x 8 nos seus valores exterior de 1 a 6, 2-7, 3-8, e 4-9, e estes quadrados exteriores pode então ser simetricamente adicionados em conjunto para dar um quadrado interior central de 5 a 10. Os valores centrais do Ho Tu são as do Lo Shu (para que eles trabalhem em conjunto), uma vez que o valor total de 15 x 2 (claro e escuro) é encontrado o número de anos no ciclo de precessão equinocial (12.960 x 2 = 25,920). O Ho Tu produz um total de 40 luz e 40 números escuros chamado os dias e as noites (as alternâncias de claro e escuro), e um total de 8 x 8 x 8 Hexagramas cuja adição simétrico oposto é igual a 8640, portanto, cada valor de um quadrado é chamado de uma temporada como ele é igual a 2160. 8640 é o número de horas em um ano de 360 dias, e 2.160 anos é igual a um aeon (12 éons = 25.920 anos).
Para validar os valores contidos nos dois mapas fluviais (Ho Tu e Lo Shu) o I Ching fornece números do Céu e da Terra, que são o 'Original Trigrams "(pai e mãe) de 1 a 10. Céu ou um Trigram com toda ininterrupta linhas (linhas claras - yang) têm números ímpares 1,3,5,7,9, e da Terra um Trigram com todas as linhas quebradas têm números pares 2,4,6,8,10. Se cada um de linhas do trigrama é dado um valor multiplicando os números do Céu e da Terra, então o valor de cada linha no céu 1 seria 1 + 2 + 3 = 6, e sua parceira no Ho Tu de Terra 6 seria 6 + 12 + 18 = 36, estes dois 'Original trigramas ", assim, produzir mais 6 Trigrams (ou crianças em todas as suas combinações) - e quando as seqüências de trigramas são colocadas em ângulos retos entre si que produzem um 8 x 8 quadrados de Hexagramas (ou cubos) que cada um tem 6 linhas de valores. A partir deste ponto simples a complexa estrutura de a matemática evolui como uma progressão hexadecimal, e é o hexágono que é o link para a carapaça de tartaruga ou tartaruga. Em textos chineses do I Ching a lua é um símbolo de água (escuridão) cujas transformações ou mudanças de criar a luz ou o fogo - o valor escuro 6 cria a luz quando o seu número é aumentado em 1. Este mesmo princípio pode ser encontrado em calendários antigos tais como o Egípcio, como o ano de 360 dias de 8640 horas foi dividido por 72 para produzir os cinco dias extras ou 120 horas em que os deuses nasceram. Demora 72 anos para os céus para mover um grau através de sua precessão.
Significado cultural de quadrados mágicos
Quadrados mágicos têm fascinado a humanidade ao longo dos tempos, e foram em torno de mais de 4.000 anos. Eles são encontrados em um número de culturas, incluindo o Egito ea Índia, gravado em pedra ou metal e usado como talismãs, a crença é que quadrados mágicos teve astrológicos qualidades e divinatórias, a sua utilização garantindo longevidade e prevenção de doenças.
O Kubera-Kolam é uma pintura piso utilizado na Índia, que tem a forma de um quadrado mágico de ordem três. Ele é essencialmente o mesmo que o Quadrado de Lo Shu, mas com 19 adicionados a cada número, dando uma constante de 72 mágica.
| 23 | 28 | 21 |
| 22 | 24 | 26 |
| 27 | 20 | 25 |
Saudita
Quadrados mágicos eram conhecidos Matemáticos árabes, possivelmente tão cedo quanto o século 7, quando os árabes entraram em contato com a cultura indiana ou do Sul da Ásia, e aprendeu matemática e astronomia indianas, incluindo outros aspectos da matemática combinatória . Também tem sido sugerido que a ideia veio através da China. Os primeiros quadrados mágicos de ordem 5 e 6 de aparecer em uma enciclopédia de Bagdá por volta de 983 dC, o Rasa'il Ihkwan al-Safa (a Enciclopédia do Brethern da Pureza); mais simples quadrados mágicos eram conhecidos por vários matemáticos árabes anteriores.
O matemático árabe Ahmad al-Buni, que trabalhou em quadrados mágicos por volta de 1200 dC, atribuído propriedades místicas para eles, embora nenhum detalhe destas supostas propriedades são conhecidas. Há também referências ao uso de quadrados mágicos em cálculos astrológicos, uma prática que parece ter se originado com os árabes.
Índia
Um quadrado mágico início bem conhecida na Índia é encontrado em Khajuraho na Parshvanath Templo Jain. Data do século 10.
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
Isto é referido como o Chautisa Yantra, uma vez que cada somas sub-quadrado a 34.
Europa
Em 1300, com base no trabalho do árabe Al-Buni, erudito bizantino grego Manuel Moschopoulos escreveu um tratado matemático sobre o assunto de quadrados mágicos, deixando de fora o misticismo de seus antecessores. Moschopoulos é pensado para ser o primeiro ocidental a ter escrito sobre o assunto. Na década de 1450 o Italiano Luca Pacioli estudou quadrados mágicos e recolhido um grande número de exemplos.
Em cerca de 1510 Heinrich Cornelius Agrippa escreveu De Occulta Philosophia, com base na Hermética e obras mágicas de Marsilio Ficino e Pico della Mirandola, e em que ele expôs sobre as virtudes mágicas de sete quadrados mágicos de ordens 3-9, cada um associado a um dos astrológicos planetas. Este livro foi muito influente em toda a Europa até o Contra-Reforma e quadrados mágicos de Agripa, às vezes chamado Kameas , continuar a ser usado dentro de magia cerimonial moderno em muito da mesma forma que ele prescreveu primeiro.
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

O uso mais comum para estes Kameas é proporcionar um padrão sobre a qual a construção do sigilos de espíritos, anjos ou demônios; as letras do nome da entidade são convertidos em números, e as linhas são traçadas através do padrão que estes números sucessivos fazer no kamea. Em um contexto mágico, o quadrado mágico termo também é aplicado a uma variedade de praças palavra ou número praças encontrado em mágica grimoires, incluindo algumas que não seguem nenhum padrão óbvio, e mesmo aqueles com diferentes números de linhas e colunas. Eles são geralmente destinados para uso como talismãs. Por exemplo os seguintes quadrados são: A Quadrado de Sator, um dos mais famosos quadrados mágicos encontrados em uma série de grimoires incluindo o Chave de Salomão; um quadrado "para superar a inveja", de O Livro do Poder; e dois quadrados de O Livro da Magia Sagrada de Abramelin o Mago, o primeiro a causar a ilusão de um palácio soberbo a aparecer, eo segundo a ser usado na cabeça de uma criança durante um angélico invocação:
|
|
|
|
Quadrado mágico de Albrecht Dürer

O fim-4 quadrado mágico em Gravura de Albrecht Dürer Melencolia I acredita-se ser o primeiro visto na arte européia. É muito semelhante a Praça de Yang Hui, que foi criado na China cerca de 250 anos antes da época de Dürer. A soma 34 pode ser encontrado nas linhas, colunas diagonais, cada um dos quadrantes, os quatro centros de quadrados, os quadrados de canto, os quatro números exteriores no sentido horário a partir dos cantos (3 + 8 + 14 + 9) e do mesmo modo o contador de quatro -clockwise (os locais de quatro rainhas nas duas soluções da 4 rainhas quebra-cabeça ), Os dois conjuntos de quatro números simétricos (2 + 8 + 9 + 15 e 3 + 5 + 12 + 14) e a soma das duas entradas médias das duas colunas e linhas externas (por exemplo, 5 + 8 + 9 + 12 ), bem como vários quartetos em forma de pipa, por exemplo, 3 + 5 + 11 + 15; os dois números no meio da linha inferior indicam a data da gravação: 1514. de Dürer Melencolia I desempenha um papel-chave na The Thief Art, um romance de Noah Charney (Atria, 2007).
| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
O quadrado mágico Sagrada Família

A fachada da Paixão Igreja da Sagrada Família, em Barcelona , projetada pelo escultor Josep Subirachs, apresenta um quadrado 4 × 4 mágica:
A constante mágica do quadrado é 33, a idade de Jesus no momento da Paixão. Estruturalmente, é muito semelhante ao quadrado mágico melancolia, mas teve os números em quatro das células reduzido em um.
| 1 | 14 | 14 | 4 |
| 11 | 7 | 6 | 9 |
| 8 | 10 | 10 | 5 |
| 13 | 2 | 3 | 15 |
Apesar de ter o mesmo padrão de soma, este não é um quadrado mágico normal, como acima, como dois números (10 e 14) são duplicados e dois (12 e 16) estão ausentes, falhando a 1 → regra n².
Tipos de quadrados mágicos e sua construção
Há muitas maneiras de construir quadrados mágicos, mas o padrão (e mais simples) caminho é seguir certas configurações / fórmulas que geram padrões regulares. Existem quadrados mágicos para todos os valores de n, com uma única exceção - é impossível construir um quadrado mágico de ordem 2. quadrados mágicos podem ser classificados em três tipos: impar, duplamente mesmo (n divisível por quatro) e isoladamente mesmo (n mesmo, mas não é divisível por quatro). Quadrados estranhos e até mesmo duplamente mágicos são fáceis de gerar; a construção de isolados até mesmo quadrados mágicos é mais difícil, mas existem vários métodos, incluindo a Método LUX para quadrados mágicos (devido a John Horton Conway) e a Strachey método para quadrados mágicos.
A teoria do grupo também foi utilizado para a construção de novas praças mágicas de uma dada ordem de um deles, consulte .
| Quantas n × n quadrados mágicos para n> 5? |
O número de diferentes n × n quadrados mágicos para n 1-5, sem contar as rotações e reflexões:
- 1, 0, 1, 880, 275.305.224 (sequência A006052 em OEIS ).
O número para n = 6 foi estimada 1,7745 × 10 19.
Um método para a construção de um quadrado mágico de ordem ímpar
A partir da coluna central da primeira linha com o número 1, o movimento fundamental para o enchimento dos quadrados é diagonalmente para cima e para a direita, um passo de cada vez. Se um quadrado preenchido é encontrado, se move verticalmente para baixo um quadrado em vez disso, em seguida, continuar como antes. Quando um movimento iria deixar a praça, que é enrolado em torno da última linha ou primeira coluna, respectivamente.
Padrões semelhantes podem também ser obtidos começando a partir de outros quadrados.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
As seguintes fórmulas ajudar a construir quadrados mágicos de ordem ímpar
| ||||||||||||
* Raízes quadradas são mais fáceis de calcular as raízes cúbicas
Exemplo:
| ||||||||||||
O "Número Médio" está sempre no fundo diagonal da esquerda para a direita superior.
O "último número" é sempre em frente ao número 1 em uma coluna ou linha externa.
Um método de construção de um quadrado mágico de ordem duplamente mesmo
Duplamente mesmo significa que n é um múltiplo de um inteiro mesmo; ou 4p, em que p é um número inteiro. por exemplo, 4, 8, 12
Padrão genérico
Todos os números são escritos em ordem da direita para a esquerda através de cada linha, por sua vez, a partir do canto superior esquerdo. Os números são, então, quer retido no mesmo lugar ou trocados com os respectivos números diametralmente opostas em um determinado padrão regular. No quadrado mágico de ordem quatro, os números nas quatro praças centrais e um quadrado em cada canto são mantidos no mesmo lugar e os outros são trocados com os seus números diametralmente opostas.
A construção de um quadrado mágico de ordem 4
Vá para a esquerda para a direita até a praça enchendo contagem e preenchendo apenas nas diagonais. Em seguida, continue indo esquerda para a direita do canto superior esquerdo da tabela e preencher a contagem regressiva de 16 ou n². Como mostrado abaixo.
|
| ||||||||||||||||||||||||||||||||||||||||
O medjig-método de construir quadrados mágicos do mesmo modo n> 4
Este método lúdico é baseado em um jogo matemático publicou 2006 chamado medjig (autor: Willem Barink, editor: Philos-Spiele). As peças do puzzle medjig quadrados são divididos em quatro quadrantes em que os números 0, 1, 2 e 3 estão espalhadas em todas as sequências. Há 18 quadrados, cada seqüência ocorre três vezes. O objetivo do puzzle é fazer 9 quadrados fora da coleção e organizá-los em um 3 x 3 "medjig-quadrado" de tal forma que a série, colunas e diagonais formadas pelos quadrantes, mostrar a soma de 9.
A maneira medjig de construção de um quadrado mágico de ordem 6 é o seguinte. Organizar um quadrado 3 x 3 medjig (por conveniência desta vez você pode escolher ilimitada de toda a coleção). Em seguida, tomar o clássico 3 x 3 quadrado mágico conhecido e dividir todos os campos de que em quatro quadrantes. Próximo preencher esses quadrantes com o número original e os seus três modulo-9 números até 36, seguindo o padrão da solução-medjig. Ao fazê-lo, o campo original com o número 8 produz os quatro subcampos com os números 8 (= 8 + 0x9), 17 (= 8 + 1X9), 26 (8 + = 2x9) e 35 (8 + = 3x9), o campo com o número 3 produz os números 3, 12, 21 e 30, etc ... Veja a ilustração abaixo.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Da mesma maneira você pode construir um quadrado mágico de ordem 8. Primeiro você tem que construir uma solução medjig 4 x 4 (soma de todas as séries, colunas e diagonais 12). E, em seguida, ampliar por exemplo, o bem conhecido Dürer 4 x 4 quadrado mágico modulo-16 a 64. Para a construção de um quadrado mágico de ordem 10 você tem que arranjar uma solução medjig 5 x 5, para os quais são necessários dois conjuntos de peças medjig . Para a ordem 12, você pode simplesmente duplicar horizontalmente e verticalmente uma solução medjig 3 x 3 e, em seguida, ampliar modulo-36-144 a ordem 6 quadrado mágico feito acima. Ordem 16 vai da mesma maneira.
A construção de quadrados panmagic
Qualquer número p na ordem de quadrado-n pode ser escrito exclusivamente sob a forma de um p + r =, com R escolhido a partir de {1, ..., n}. Note-se que devido a esta restrição, um e r não são o quociente habitual e resto da divisão de p por n. Por conseguinte, o problema da construção pode ser dividido em dois problemas mais fácil de resolver. Então, construir dois correspondentes grades quadrados de propriedades de ordem n panmagic satisfatória, uma para os números-A (0, ...., N-1), e um para os números-R (1, ...., N). Isso requer um monte de confusão, mas pode ser feito. Quando bem sucedida, combiná-los em um - panmagic - quadrado. Van den Essen e muitos outros suposto esta também foi a maneira como o grande Benjamin Franklin (1706-1790) construiu suas famosas praças franklin. Três quadrados panmagic são mostrados abaixo. Os dois primeiros quadrados foram construídos de Abril de 2007 por Barink, o terceiro é alguns anos mais velho, e vem de Donald Morris, que utilizou, como ele supõe, a maneira franklin de construção.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A ordem 8 satisfaz todas as propriedades panmagic quadrados, incluindo os franklin. É composto por 4 unidades de 4x4 perfeitamente panmagic. Note-se que ambos os pedidos 12 quadrados mostram a propriedade de que qualquer linha ou coluna pode ser dividido em três partes tendo uma soma de 290 (= 1/3 da soma total de uma linha ou coluna). Esta propriedade compensa a ausência da propriedade Franklin panmagic mais padrão que qualquer meia linha ou coluna mostra a soma de 1/2 do total. Para o resto do fim de 12 praças diferem um quadrado lot.The Barink 12x12 é composta por 9 unidades 4x4 perfeitamente panmagic, além disso quaisquer quatro números consecutivos começando em qualquer lugar estranho em uma linha ou coluna mostram uma soma de 290. O 12x12 quadrado Morris carece estas propriedades, mas, pelo contrário, mostra franklindiagonals constantes. Para uma melhor compreensão do Construindo decompor os quadrados tal como descrito acima, e ver como ele foi feito. E observar a diferença entre as construções Barink por um lado, e a construção Morris / Franklin, por outro lado.
No livro Matemática no Time-Life Science Biblioteca Série, quadrados mágicos de Euler e Franklin são mostrados. Franklin projetei este para que qualquer subconjunto de quatro quadrados (qualquer quatro quadrados contíguos que formam um quadrado maior, ou quaisquer quatro quadrados equidistantes do centro) total de 130. Na Praça de Euler, as linhas e colunas cada total de 260, e no meio do caminho eles totalizam 130 - e um xadrez cavaleiro, fazendo seus movimentos em forma de L na praça, pode tocar todas as 64 caixas em ordem numérica consecutiva.
A construção de um quadrado mágico usando algoritmos genéticos
Um quadrado mágico pode ser construído usando algoritmos genéticos. Este é um processo de tentativa e erro elegante em que uma população inicial de quadrados mágica com valores aleatórios são gerados. As aptidões destes quadrado mágico individuais são calculados com base no "achatamento" do quadrado mágico, ou seja, o grau de desvio nas somas das linhas, colunas e diagonais. A população de quadrados mágicos vai cruzar (valores de troca) de uma forma coerente com a genética, com base na pontuação aptidão dos quadrados mágicos. Assim, quadrados mágicos com maior pontuação de fitness terá uma maior probabilidade de se reproduzir. No processo de cruzamentos onde os quadrados mágicos trocar seus valores, um fator de mutação é introduzida, imitando mutação genética na natureza. Esta mutação serão incluídos ou excluídos naturalmente a partir da solução em função da sua contribuição para a aptidão do quadrado mágico. A próxima geração da população quadrado mágico é novamente calculada para a sua aptidão, e esse processo continua até que seja encontrada uma solução.
Generalizações
Restrições extras
Certas restrições adicionais podem ser impostas quadrados mágicos. Se não só as diagonais principais, mas também as diagonais quebrados para resumir a constante mágica, o resultado é um praça panmagic. Se levantando cada número para certos poderes produz outro quadrado mágico, o resultado é uma bimagic, uma trimagic, ou, em geral, uma praça multimagic.
Diferentes restrições
Às vezes, as regras para quadrados mágicos estão relaxados, de modo que apenas as linhas e colunas, mas não necessariamente as diagonais somar a constante mágica. Em heterosquares e praças antimagia, os 2 n + 2 somas devem ser todos diferentes.
Outras operações
Em vez de adicionar os números em cada fila, coluna e diagonal, pode-se aplicar alguma outra operação. Por exemplo, um quadrado mágico multiplicativa tem um produto da constante de números.
|
| ||||||||||||||||||||||||||||||||
Outras formas mágicas
Outros formatos quadrados do que pode ser considerado, o que resulta, por exemplo, em estrelas mágicas e hexágonos magia. Subindo no resultado de dimensão em cubos mágicos, tesseracts mágicos e outros hypercubes magia.
Edward Shineman, uma forma mágica de renome internacional construcionista, desenvolveu ainda um outro projeto na forma de diamantes mágicos. Ele fez muitos deles para fins comemorativas e históricas, e também experimentou com outro casal retângulo auto-contido / combinações quadrados, figuras "clareamento" em forma de L, e muito mais. Os diamantes foram feitas em honra de eventos e pessoas que vão de Tiger Woods para Ronald Reagan, da Universidade de Cornell aniversário de a família aniversários especiais. Várias de suas obras foram apresentados em livros quadrados mágicos, bem como várias publicações em The Journal of Mathematics recreativas. Uma matriz de suas contribuições mágicas podem ser encontradas em eds-magic-squares.com.
Extensões combinados
Pode-se combinar duas ou mais das extensões acima, resultando em objectos tais como hypercubes multimagic multiplicativos. Pouco parece ser conhecido sobre este assunto.
Problemas relacionados
Ao longo dos anos, muitos matemáticos, incluindo Euler e Cayley têm trabalhado em quadrados mágicos, e descobriu relações fascinantes.
Quadrado mágico de primos
Rudolf Ondrejka (1928-2001) descobriu o seguinte 3x3 quadrado mágico de números primos , neste caso, nove Chen primos:
| 17 | 89 | 71 |
| 113 | 59 | 5 |
| 47 | 29 | 101 |
O Green-Tao teorema implica que há arbitrariamente grandes quadrados mágicos que consistem de números primos.
problema n-rainhas
Em 1992, Demirörs, Rafraf, e Tanik publicou um método para a conversão de alguns quadrados mágicos em Soluções N-rainhas, e vice-versa.
Data quadrado mágico
A praça data mágica é um quadrado de 4 × 4 mágica em que os números em uma determinada data (por exemplo, 15 de abril de 1707) são utilizados para construir a primeira fileira (4, 15, 17, 07). O constante mágica (M) de um 4 × 4 quadrado mágico 'normal' é 34. Se os quatro números em uma data que não se somam a 34, não podemos construir um quadrado mágico 'normal' para essa data. No exemplo acima, M = 43:
| 4 | 15 | 17 | 07 |
| 5 | 19 | 13 | 6 |
| 20 | 9 | 2 | 12 |
| 14 | 0 | 11 | 18 |
A única diferença entre um quadrado mágico e um quadrado mágico data é que, em uma data mágica repetição quadrado de números não é permitido em qualquer linha, exceto o primeiro, enquanto que em um quadrado mágico 'normal', a repetição não é permitido em qualquer linha .
Número / Word quadrado mágico
A Number / Word praça combinação mágica é construído usando as três regras seguintes:
- Faça um quadrado mágico normal da ordem de 3 utilizando quaisquer números.
- Contar o número de letras de cada número e substituir o número com essa contagem.
- A nova praça também deve ser mágica.
Um exemplo de um tal quadrado é mostrado abaixo:
|
|
| ||||||||||||||||||||||||||||||||||||
Problema Tarry-Escott
Por uma estranha coincidência, a 3 × 3 quadrado mágico contém uma solução para o Problema Tarry-Escott.
| 4 | 9 | 2 |
| 3 | 5 | 7 |
| 8 | 1 | 6 |
Prepare dois números define a partir do quadrado mágico acima através da combinação de números de linhas e últimos últimas colunas nas instruções no sentido horário e sentido anti-horário:
- {492, 276, 618, 834}
- {294, 438, 816, 672}.
Tarry-Escott Solução:
- 492 1 + 276 618 1 + 1 + 1 = 834 + 294 1 438 1 816 + 1 + 672 1
- 492 2 + 2 276 + 2 618 + 834 = 2 294 2 + 2 438 + 2 816 + 2 672
- 3 492 + 3 276 + 3 618 + 834 = 294 3 3 + 438 + 3 816 3 + 3 672.
Magic Squares em literatura contemporânea
No capítulo 2 de A Grande Cérebro está de volta por John D. Fitzgerald, Tom, aliás o "Grande Brain", lembra-se de ter sido dito por um professor sobre um quadrado mágico. Depois de trabalhar nele durante três dias, ele vem com a Ordem 3, Sum 15 quadrado. Ele, então, configura o "jogo dos números", arredondando seus amigos e explicando o conceito, cobrando 10 centavos para jogar com um prêmio de 50 centavos para qualquer um que pode resolvê-lo dentro de dois dias, entregando uma folha com a grade de 3 * 3 e o números de um a nove para cada jogador, e dando permissão a todos os participantes para obter a ajuda de seus pais. Pensando que vai ser fácil, todas as 20 crianças presentes, incluindo seu irmão John (o narrador) optar por jogar e dar-lhe um centavo. John mostra-o a seu pai, o único graduado da faculdade na cidade. Seu pai explica que a primeira coisa a fazer é fazer uma lista de todas as combinações de três números de 1 a 9, que totalizam 15, excluindo aqueles em que um número é usado mais de uma vez. Em seguida, (mostrando falta de conhecimentos sobre o assunto), ele diz que você tem que "continuar tentando as diferentes combinações até chegar a resposta certa." John faz parte da lista, e gasta cada momento livre que ele tem ao longo dos próximos dois dias tentando colocar as combinações juntos, sem sucesso. Seu pai diz-lhe para fazê-lo pela eliminação e começar com os três praças do centro, mas não elaborou. Após dois dias, ninguém tem resolvido, e alguns acreditam que ele não pode ser feito. Mas quando o prazo passa e não há vencedores, Tom revela a resposta.
Em O romance de Steve Martin The Pleasure of My Company, o personagem principal Daniel Pecan Cambridge constrói quadrados mágicos como uma forma de relaxar.