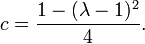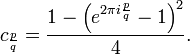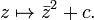Mandelbrot set
Informações de fundo
Crianças SOS tentou tornar o conteúdo mais acessível Wikipedia por esta selecção escolas. Crianças SOS é a maior doação de caridade do mundo órfãos e crianças abandonadas a chance da vida familiar.

O conjunto de Mandelbrot é um conjunto de aponta no plano complexo , o limite de que forma um fractal . Matematicamente, o conjunto de Mandelbrot pode ser definida como o conjunto de valores A c complexas para as quais a órbita de 0 sob iteração do complexo quadrático polinômio x n + 1 = 2 x n + c restos delimitada.
Eg. c = 1 dá a sequência de 0, 1, 2, 5, 26, ... que leva até ao infinito. Como esta sequência é ilimitado, 1 não é um elemento do conjunto de Mandelbrot.
Por outro lado, c = i dá a sequência de 0, i, (-1 + i), -i, (-1 + i), -i ... que é delimitada, e, portanto, pertence ao grupo de Mandelbrot.
Quando calculada e representada graficamente no plano complexo, o grupo de Mandelbrot é visto como tendo um limite de elaborada, que não simplifica a qualquer dado ampliação. Isso qualifica a fronteira como um fractal.
O conjunto de Mandelbrot tornou-se fora populares matemática tanto por seu apelo estético e por ser uma estrutura complicada decorrente de uma definição simples. Benoît Mandelbrot e outros trabalharam duro para se comunicar esta área da matemática para o público.
História
O conjunto de Mandelbrot tem seu lugar na dinâmicas complexas, um campo primeiro investigado pelos matemáticos franceses Pierre Fatou e Gaston Julia no início do século 20. As primeiras fotos dele foram desenhados em 1978 por Robert Brooks e Peter Matelski como parte de um estudo de Grupos kleinianas.
Mandelbrot estudou o parâmetro de espaço polinômios quadráticos em um artigo que apareceu em 1980. O estudo matemático do grupo de Mandelbrot realmente começou com o trabalho pelos matemáticos Adrien Douady e John H. Hubbard, que estabeleceu muitas das suas propriedades fundamentais e nomeou o set em honra de Mandelbrot.
Os matemáticos Heinz-Otto e Peitgen Peter Richter tornou-se conhecido por promover o set com fotografias brilhantes, livros, e uma galeria de touring.
O artigo de capa do agosto 1985 Scientific American apresentou uma imagem criada por Mandelbrot, Peitgen, e Hubbard.
O trabalho de Douady e Hubbard coincidiu com um aumento enorme no interesse na dinâmica complexa e matemática abstrata, eo estudo do conjunto de Mandelbrot tem sido uma peça central deste campo desde então. Uma lista exaustiva de todos os matemáticos que têm contribuído para a compreensão desse conjunto, desde então, está além do escopo deste artigo, mas essa lista inclui, nomeadamente, Mikhail Lyubich,, Curt McMullen, John Milnor, Mitsuhiro Shishikura, e Jean-Christophe Yoccoz.
Definição formal
O conjunto de Mandelbrot  é definido por uma família de polinômios quadrática complexa
é definido por uma família de polinômios quadrática complexa
dado por
 ,
,
onde  é um parâmetro complexo. Para cada
é um parâmetro complexo. Para cada  , Considera-se o comportamento da sequência
, Considera-se o comportamento da sequência  obtido pela iterating
obtido pela iterating 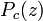 Começando às ponto crítico
Começando às ponto crítico 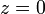 , Que quer escapa ao infinito ou fica dentro de um disco de algum raio finito. O conjunto de Mandelbrot é definido como o conjunto de todos os pontos
, Que quer escapa ao infinito ou fica dentro de um disco de algum raio finito. O conjunto de Mandelbrot é definido como o conjunto de todos os pontos  de tal modo que a sequência de cima não escapa para o infinito.
de tal modo que a sequência de cima não escapa para o infinito.

Mais formalmente, se  denota o n º de iterate
denota o n º de iterate 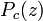 (Ou seja
(Ou seja 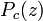 composto com si n vezes), o conjunto de Mandelbrot é o subconjunto do plano complexo dada por
composto com si n vezes), o conjunto de Mandelbrot é o subconjunto do plano complexo dada por
Matematicamente, o conjunto de Mandelbrot é apenas um conjunto de números complexos. Um determinado número complexo  ou pertencente a
ou pertencente a 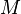 ou não. Uma imagem do conjunto de Mandelbrot pode ser feita por coloração todos os pontos
ou não. Uma imagem do conjunto de Mandelbrot pode ser feita por coloração todos os pontos  que pertencem
que pertencem 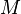 preto, e todos os outros pontos de branco. As imagens mais coloridas geralmente vistos são gerados por pontos corantes não no conjunto de acordo com o quão rápida ou lentamente a seqüência
preto, e todos os outros pontos de branco. As imagens mais coloridas geralmente vistos são gerados por pontos corantes não no conjunto de acordo com o quão rápida ou lentamente a seqüência 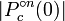 diverge para o infinito. Veja a seção sobre desenhos de computador abaixo para mais detalhes.
diverge para o infinito. Veja a seção sobre desenhos de computador abaixo para mais detalhes.
O conjunto de Mandelbrot também pode ser definida como a conexão locus da família de polinómios 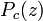 . Isto é, é o subconjunto do plano complexo que consiste naqueles parâmetros
. Isto é, é o subconjunto do plano complexo que consiste naqueles parâmetros  para o qual o Julia conjunto de
para o qual o Julia conjunto de  é ligado.
é ligado.
Propriedades básicas
O conjunto de Mandelbrot é um conjunto compacto , contida no disco fechado de raio de 2 em torno da origem. Na verdade, um ponto  pertence ao conjunto de Mandelbrot, se e somente se
pertence ao conjunto de Mandelbrot, se e somente se  para todos
para todos  . Em outras palavras, se o valor absoluto de
. Em outras palavras, se o valor absoluto de  nunca se torna maior do que 2, a sequência vai escapar para o infinito.
nunca se torna maior do que 2, a sequência vai escapar para o infinito.

O cruzamento de 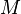 com o eixo real é precisamente o intervalo
com o eixo real é precisamente o intervalo ![[-2, 0.25] \,](../../images/214/21445.png) . Os parâmetros ao longo deste intervalo pode ser colocado em um-para-um correspondência com aqueles do real família logística,
. Os parâmetros ao longo deste intervalo pode ser colocado em um-para-um correspondência com aqueles do real família logística,
A correspondência é dada pela
Na verdade, isto dá uma correspondência entre todo o espaço de parâmetros da família logística e que do conjunto de Mandelbrot.
A área do conjunto de Mandelbrot é estimada em 1,506 ± 0,000 77 591 000 08.
Douady e Hubbard têm mostrado que o conjunto de Mandelbrot é ligado. Na verdade, eles construíram uma explícita isomorfismo conformada entre o complemento do conjunto de Mandelbrot e o complemento do disco unidade fechada. Mandelbrot tinha inicialmente suspeitado de que o conjunto de Mandelbrot é desconectado. Esta conjectura foi baseado em imagens de computador gerados por programas que não são capazes de detectar os filamentos finos que ligam diferentes partes 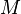 . Após mais experimentos, ele revisou sua conjectura, decidindo que
. Após mais experimentos, ele revisou sua conjectura, decidindo que 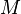 deve ser conectado.
deve ser conectado.
A fórmula para a dinâmica uniformização do complemento do conjunto de Mandelbrot, decorrente de Douady e Hubbard prova da conexão de 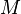 , Dá origem a raios externos do grupo de Mandelbrot. Estes raios podem ser utilizados para estudar o conjunto Mandelbrot em termos combinatórios e formar a espinha dorsal da Yoccoz parapuzzle.
, Dá origem a raios externos do grupo de Mandelbrot. Estes raios podem ser utilizados para estudar o conjunto Mandelbrot em termos combinatórios e formar a espinha dorsal da Yoccoz parapuzzle.
O limite do conjunto de Mandelbrot é exatamente o bifurcação lócus da família quadrática; isto é, o conjunto de parâmetros  para os quais a dinâmica muda abruptamente sob pequenas alterações de
para os quais a dinâmica muda abruptamente sob pequenas alterações de  Pode ser construído como o limite definido de uma sequência de curvas algébricas planas, as curvas de Mandelbrot, do tipo geral conhecido como lemniscates polinomiais. As curvas Mandelbrot são definidos pela configuração p 0 = z, p = n p n-1 + Z 2, e, em seguida, interpretando o conjunto de pontos | p n (z) | = 1 no plano complexo, como uma curva no real cartesiano plano de grau 2 n + 1 em x e y.
Pode ser construído como o limite definido de uma sequência de curvas algébricas planas, as curvas de Mandelbrot, do tipo geral conhecido como lemniscates polinomiais. As curvas Mandelbrot são definidos pela configuração p 0 = z, p = n p n-1 + Z 2, e, em seguida, interpretando o conjunto de pontos | p n (z) | = 1 no plano complexo, como uma curva no real cartesiano plano de grau 2 n + 1 em x e y.
Outras propriedades
Os principais cardioides e período bulbos

Ao olhar para uma imagem do conjunto de Mandelbrot, um imediatamente percebe a grande cardióide região em forma no centro. Este cardióide principal é a região de parâmetros  para qual
para qual  tem um atraindo ponto fixo. Ele consiste de todos os parâmetros de forma
tem um atraindo ponto fixo. Ele consiste de todos os parâmetros de forma
para alguns  no disco unidade aberta.
no disco unidade aberta.
À esquerda do cardióide principal, ligada a ela no ponto  , Uma lâmpada de forma circular é visível. Esta lâmpada é composto por esses parâmetros
, Uma lâmpada de forma circular é visível. Esta lâmpada é composto por esses parâmetros  para qual
para qual  tem um atraindo ciclo de período 2. Este conjunto de parâmetros é um círculo real, ou seja, que de raio em torno de 1/4 -1.
tem um atraindo ciclo de período 2. Este conjunto de parâmetros é um círculo real, ou seja, que de raio em torno de 1/4 -1.
Há infinitamente muitos outros tangente lâmpadas ao cardióide principal: para cada número racional  , Com p e q primos entre si, não há tal lâmpada que é tangente ao parâmetro
, Com p e q primos entre si, não há tal lâmpada que é tangente ao parâmetro

Este bolbo é chamado o  -bulb do grupo de Mandelbrot. É constituída de parâmetros que têm um ciclo de atrair período
-bulb do grupo de Mandelbrot. É constituída de parâmetros que têm um ciclo de atrair período  e número de rotação combinatória
e número de rotação combinatória  . Mais precisamente, o
. Mais precisamente, o  periódico Fatou componentes que contêm o ciclo atraindo todos toque em um ponto comum (comumente chamado de
periódico Fatou componentes que contêm o ciclo atraindo todos toque em um ponto comum (comumente chamado de 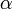 ponto -Fixed). Se nós rotular estes componentes
ponto -Fixed). Se nós rotular estes componentes  na orientação anti-horário, em seguida
na orientação anti-horário, em seguida  mapeia o componente
mapeia o componente 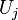 para o componente
para o componente  .
.

A mudança de comportamento que ocorre no  é conhecido como um bifurcação: os atraindo ponto fixo "colide" com um q -Ciclo período repelente. À medida que passam através do parâmetro de bifurcação para o
é conhecido como um bifurcação: os atraindo ponto fixo "colide" com um q -Ciclo período repelente. À medida que passam através do parâmetro de bifurcação para o  -bulb, o ponto fixo atraindo se transforma em um ponto de repulsão fixo (o
-bulb, o ponto fixo atraindo se transforma em um ponto de repulsão fixo (o  ponto -Fixed), eo período -Ciclo q torna-se atrair.
ponto -Fixed), eo período -Ciclo q torna-se atrair.
Componentes hiperbólicas
Todas as lâmpadas que encontramos na seção anterior eram componentes interiores do conjunto de Mandelbrot em que os mapas  tem um ciclo periódico atraindo. Esses componentes são chamados de componentes hiperbólicas.
tem um ciclo periódico atraindo. Esses componentes são chamados de componentes hiperbólicas.
Conjectura-se que estas são as únicas regiões do interior 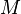 . Este problema, conhecido como densidade de hiperbolicidade, pode ser aberto o problema mais importante no campo da dinâmica de complexos. Componentes não-hiperbólicos hipotético do conjunto de Mandelbrot são muitas vezes referidos como componentes "queer".
. Este problema, conhecido como densidade de hiperbolicidade, pode ser aberto o problema mais importante no campo da dinâmica de complexos. Componentes não-hiperbólicos hipotético do conjunto de Mandelbrot são muitas vezes referidos como componentes "queer".
Para polinômios quadráticos reais, esta pergunta foi respondida positivamente na década de 1990 de forma independente por Lyubich e por Graczyk e Świątek. (Note-se que componentes hiperbólicas de interseção do eixo reais correspondem exactamente às janelas periódicas no Diagrama de Feigenbaum. Portanto, este resultado indica que essas janelas existem perto de cada parâmetro no diagrama.)
Nem todos os componentes hiperbólica pode ser alcançado por uma sequência de bifurcações diretos do principal cardióide do conjunto de Mandelbrot. No entanto, esse componente pode ser alcançado por uma sequência de bifurcações directas da principal cardioid de um pouco de cópia Mandelbrot (veja abaixo).
Ligações locais
Conjectura-se que o conjunto de Mandelbrot é localmente ligado. Esta conjectura famoso é conhecido como MLC (por Mandelbrot Conectada localmente). Pelo trabalho de Adrien Douady e John H. Hubbard, essa conjectura resultaria em um modelo simples abstrato "disco pinçado" do conjunto de Mandelbrot. Em particular, isso implicaria a conjectura hiperbolicidade importante mencionado acima.
O célebre obra de Jean-Christophe Yoccoz estabelecido conectividade local do grupo de Mandelbrot em todos os finito-renormalizável parâmetros; isto é, falando grosseiramente, aquelas que estão contidos apenas em um número finito de pequenas cópias Mandelbrot. Desde então, a conectividade local tem sido provado em muitos outros pontos de 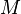 , Mas a conjectura completa ainda está aberta.
, Mas a conjectura completa ainda está aberta.
Auto-similaridade

 .
. 
O conjunto de Mandelbrot é auto-similar sob ampliação nos bairros da Misiurewicz pontos. É também para ser conjecturado auto-semelhante ao redor generalizada Feigenbaum pontos (por exemplo, -1,401155 ou -.1528 + 1.0397i), no sentido de convergir para um conjunto limite.

O conjunto de Mandelbrot, em geral, não é estritamente auto-semelhante, mas que é quase auto-semelhante, como pequenas versões ligeiramente diferentes de si podem ser encontrados em pequenas escalas arbitrariamente.
As pequenas cópias do conjunto de Mandelbrot são todos um pouco diferente, principalmente por causa dos fios finos que ligam-los para o corpo principal do conjunto.
Mais resultados
O Dimensão do hausdorff limite do conjunto de Mandelbrot é igual a 2, tal como determinado por um resultado de Mitsuhiro Shishikura. Não se sabe se o limite do jogo de Mandelbrot tem planar positiva Medida de Lebesgue.
No Modelo Blum-Shub-Smale de computação real, o conjunto de Mandelbrot não é computável, mas seu complemento é computably enumeráveis. No entanto, muitos objectos simples (por exemplo, o gráfico de exponenciação) também não são calculável no modelo BSS. No momento não se sabe se o conjunto de Mandelbrot é computável em modelos de computação real com base no análise computável, que correspondem mais de perto com a noção intuitiva de "traçar o conjunto por um computador." Hertling mostrou que o conjunto de Mandelbrot é computável neste modelo, se a conjectura hiperbolicidade é verdade.
Relacionamento com conjuntos de Julia

Como uma consequência da definição do conjunto de Mandelbrot, existe uma correspondência próxima entre a geometria do conjunto de Mandelbrot num dado ponto e a estrutura das correspondentes Julia definido.
Este princípio é explorada no resultado de praticamente todos profundas sobre o conjunto de Mandelbrot. Por exemplo, Shishikura prova que, para um conjunto denso de parâmetros no limite do conjunto de Mandelbrot, o conjunto de Julia tem Dimensão hausdorff dois, e, em seguida, transfere esta informação ao plano de parâmetro. Da mesma forma, Yoccoz primeira prova a conectividade local de conjuntos de Julia, antes de estabelecer-lo para o grupo de Mandelbrot com os parâmetros correspondentes. Adrien Douady frases este princípio como
Plough no plano dinâmico e colheita no espaço de parâmetros.
Geometria

Lembre-se que, para cada número racional  , Onde
, Onde  e
e  são relativamente primos, existe um componente de hiperbólica período
são relativamente primos, existe um componente de hiperbólica período  bifurcando do cardióide principal. A parte do conjunto de Mandelbrot ligado ao cardióide principal neste ponto de bifurcação é chamado de p / q-membro. Computador experiências sugerem que o diâmetro do membro tende para zero como
bifurcando do cardióide principal. A parte do conjunto de Mandelbrot ligado ao cardióide principal neste ponto de bifurcação é chamado de p / q-membro. Computador experiências sugerem que o diâmetro do membro tende para zero como  . A melhor estimativa atual é conhecido o famoso Yoccoz-desigualdade, que afirma que o tamanho tende a zero como
. A melhor estimativa atual é conhecido o famoso Yoccoz-desigualdade, que afirma que o tamanho tende a zero como  .
.
Um período  -limb terá
-limb terá  "Antenas" na parte superior de seu membro. Podemos, assim, determinar o período de uma determinada lâmpada contando essas antenas.
"Antenas" na parte superior de seu membro. Podemos, assim, determinar o período de uma determinada lâmpada contando essas antenas.
Generalizações

Às vezes, a conexão de outros loci do que a família quadrática famílias também são referidos como o Mandelbrot define dessas famílias.
O loci conexão das famílias polinomiais unicritical  para
para  são freqüentemente chamados de conjuntos Multibrot.
são freqüentemente chamados de conjuntos Multibrot.

Para as famílias gerais de funções holomorfas, o limite do conjunto de Mandelbrot generaliza para o locus de bifurcação, que é um objecto natural para estudar mesmo quando o locus de ligação não é útil.
Também é possível considerar a construções semelhantes no estudo de mapeamento não analíticos. De particular interesse é o tricorn, o locus conexão da família anti-holomorphic
O tricorn (também chamado às vezes o conjunto Mandelbar) foi encontrado por Milnor em seu estudo sobre fatias de parâmetros de polinômios cúbicos reais. Não está ligado localmente. Esta propriedade é herdada pelo locus conexão de polinômios cúbicos reais.
Desenhos de computador


Algoritmos:
- Escapar algoritmo de tempo
- versão boolean (chama M-set e seu exterior usando 2 cores) = algoritmo de Mandelbrot
- discreta (inteiro) version = método de ajuste do nível (LSM / M); chama set e cor bandas Mandelbrot em seu exterior
- versão contínua
- versão curvas de nível = empates lemniscates de Mandelbrot = limites de conjuntos de nível
- decomposição do exterior de Mandelbrot set
- potencial complexo
- Hubbard-Douady (real) potencial de Mandelbrot set (CPM / M) - parte radial do potencial complexo
- ângulo externo de Mandelbrot set - parte angular do potencial complexo
- abstrato set-M
- Método de estimação Distância de Mandelbrot set
- distância estimativa exterior = algoritmo Milnor (DEM / M)
- interior estimativa distância
- algoritmo usado para explorar interior de Mandelbrot set
- período de componentes hiperbólicas
- multiplicador da órbita periódica (raios internos (ângulo) e raio intenal)
- bof61 e bof60
Cada algoritmo pode ser implementado em ou sequencial versão paralela. Simetria de espelho pode ser utilizada para cálculos de velocidade plano .
| Wikibooks tem um livro sobre o tema de: Fractals |
Escapar algoritmo de tempo
O algoritmo mais simples para a geração de uma representação do conjunto de Mandelbrot é conhecida como o algoritmo de "escapar tempo". Um cálculo de repetição é executada para cada ponto x, y na área do terreno e com base no comportamento de cálculo que, uma cor é escolhido para o pixel.
O X e Y localização de cada ponto de partida são utilizados como valores de repetição, ou iteração de cálculo (descrito em detalhe abaixo). O resultado de cada iteração seja usado como os valores iniciais para a próxima. Os valores são verificados durante cada iteração para ver se eles atingiram um estado crítico 'escape'. Se esta condição é atingida, o cálculo for interrompido, o elemento de imagem é tirada, e os próximos ponto x, y é examinada. Para alguns valores iniciais, escape ocorre rapidamente, depois de apenas um pequeno número de iterações. Para outros valores a partir, pode levar centenas ou milhares de iterações para escapar. Para valores dentro do conjunto de Mandelbrot, escape nunca ocorrerá. O programador ou usuário deve escolher a quantidade de interação, ou 'profundidade', eles deseja examinar. Quanto maior o número máximo de iterações, mais detalhes e sutileza surgem na imagem final, mas quanto mais tempo vai demorar para calcular a imagem.
A cor de cada ponto representa a rapidez com que os valores atingiram o ponto de fuga. Muitas vezes, o preto é usado para mostrar valores que não conseguem escapar antes do limite de iteração e cores gradualmente mais brilhantes são usados para pontos que escapam. Isto dá uma representação visual de quantos ciclos foram necessários antes de alcançar a condição de fuga.
Para programadores
A definição do conjunto de Mandelbrot, juntamente com as suas propriedades básicas, sugere um algoritmo simples para fazer um desenho do conjunto de Mandelbrot. A região do plano complexo que estamos a considerar é subdividida em um certo número de pixels. Para colorir qualquer pixel, deixe-  Ser o ponto médio daquele pixel. Temos agora uma iteração do valor crítico
Ser o ponto médio daquele pixel. Temos agora uma iteração do valor crítico  sob
sob  , Verificando a cada passo se o ponto de órbita tem módulo maior do que 2.
, Verificando a cada passo se o ponto de órbita tem módulo maior do que 2.
Se este for o caso, sabemos que o O ponto médio não pertencem ao conjunto de Mandelbrot, e nós colorir nosso pixel. (Ou nós colorir branco para obter a imagem matemática simples ou colori-la de acordo com o número de iterações usadas para obter as imagens coloridas conhecidas). Caso contrário, continuamos a iteração por um determinado (grande, mas fixo) número de passos, após o que nós decidimos que o nosso parâmetro é "provavelmente" no conjunto de Mandelbrot, ou pelo menos muito próximo a ele, e colorir o pixel preto.
Em pseudocódigo, este algoritmo ficaria da seguinte forma.
Para cada pixel na tela fazer: {x = x0 = x coordenada de pixels y = y0 = y coordenada de pixel de iteração = 0 max_iteration = 1000 enquanto (x * x + y * y <= (2 * 2 ) E iteração <max_iteration) {xtemp = x * x - y * y + x0 y = 2 * x * y + x = y0 xtemp iteração = iteração + 1} if (iteração == max_iteration), então color = cor mais preto = iteração plot (x0, y0, cor)} onde, para relacionar o pseudocódigo  e
e  :
:
e por isso, como pode ser visto no pseudocódigo no cálculo de x e y:
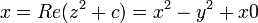 e y =
e y = 
Para obter imagens coloridas do conjunto, a atribuição de uma cor para cada valor do número de iterações executadas podem ser feitas utilizando um de uma variedade de funções (linear, exponencial, etc). Uma maneira prática de fazê-lo, sem abrandar os cálculos, é usar o número de iterações executadas como uma entrada para uma tabela paleta de cores de consulta inicializado na inicialização. Se a tabela de cores tem, por exemplo, 500 entradas, então você pode usar n mod 500, onde n é o número de iterações, para selecionar a cor a ser usada. Você pode inicializar a matriz paleta de cores de várias maneiras diferentes, dependendo do que característica especial do comportamento de fuga que você deseja enfatizar graficamente.
Contínuo coloração (liso)
The Escape Tempo Algoritmo é popular por sua simplicidade. No entanto, ele cria faixas de cores, que pode diminuir o valor de uma imagem. Isso pode ser corrigido usando o Normalized contagem de iteração do algoritmo, que prevê uma transição suave de cores entre iterações. A equação é

onde n é o número de iterações para z, B é o raio de resgate (que é normalmente dois para um conjunto de Mandelbrot, mas que pode ser alterado), e P é a potência para o qual Z é gerado no conjunto de Mandelbrot equação (z n = 1 z n P + C, P é geralmente 2). Outra equação para esta é

Note-se que esta nova equação é mais simples do que o primeiro, mas ele só funciona para conjuntos de Mandelbrot com um raio de resgate de 2 e uma potência de 2.
Embora este algoritmo é relativamente simples de implementar (usando equação), existem algumas coisas que têm de ser tomadas em consideração. Em primeiro lugar, as duas equações retornar um fluxo contínuo de números. No entanto, cabe a você decidir sobre a forma como os valores de retorno será convertida em uma cor. Algum tipo de método para a fundição de estes números em um gradiente deve ser desenvolvido. Por outro lado, recomenda-se que em alguns iterações adicionais são feitas de modo a que z pode crescer. Se parar a iteração assim que escapa z, não há a possibilidade de que o algoritmo de suavização não irá funcionar.
Estimativas de distância
Pode-se calcular a distância a partir do ponto c (em exterior ou interior) até ao ponto mais próximo da limite de Mandelbrot.
Estimativa Exterior distância
A prova da ligação do conjunto de Mandelbrot, de facto, dá uma fórmula para a uniformiza�o mapa do de complemento  (E o derivado deste mapa). Pelo Koebe 1/4 teorema, pode-se então calcular a distância entre o ponto médio do nosso pixels e o grupo de Mandelbrot até um fator de quatro.
(E o derivado deste mapa). Pelo Koebe 1/4 teorema, pode-se então calcular a distância entre o ponto médio do nosso pixels e o grupo de Mandelbrot até um fator de quatro.
Em outras palavras, desde que o número máximo de iterações é suficientemente elevado, obtém-se uma imagem do Mandelbrot com as seguintes propriedades:
- Cada pixel, que contém um ponto do conjunto de Mandelbrot é de cor preta.
- Cada pixel, que é de cor preta fica perto do conjunto de Mandelbrot.
A estimativa de distância de um c pixel (um número complexo) a partir do conjunto de Mandelbrot é dada por
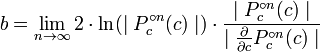
onde
 apoia polinomial quadrática complexa
apoia polinomial quadrática complexa  significa n iterações de
significa n iterações de  ou
ou 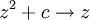 , Começando com Z = c:
, Começando com Z = c: 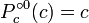 ,
,  ;
;  é o derivado de
é o derivado de  no que diz respeito a c. Este derivado pode ser encontrado a partir de
no que diz respeito a c. Este derivado pode ser encontrado a partir de  e depois
e depois  . Isso pode ser facilmente verificada usando a regra da cadeia para o derivado.
. Isso pode ser facilmente verificada usando a regra da cadeia para o derivado.
Do ponto de vista de um matemático, esta fórmula só funciona no limite em que n vai para o infinito, mas as estimativas muito razoáveis podem ser encontrados com apenas algumas iterações adicionais após as principais saídas de loop.
Uma vez b for encontrado, pelo Koebe 1/4-teorema, sabemos não há nenhum ponto de o grupo de Mandelbrot com a distância c menor do que b / 4.
Estimativa distância Interior
Também é possível calcular a distância de um (ou seja, interior) ponto limitly periódica para o limite do jogo de Mandelbrot. A estimativa é dada por 
onde
 é o período,
é o período,  é o ponto a ser estimada,
é o ponto a ser estimada, 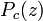 é o polinomial quadrática complexa
é o polinomial quadrática complexa 
 é
é  composições
composições  , Começando com
, Começando com 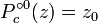
 é qualquer de a
é qualquer de a  pontos que fazem a atrator das iterações
pontos que fazem a atrator das iterações  começando com
começando com  ;
;  satisfaz
satisfaz  ,
,  ,
,  ,
,  e
e  são derivados de várias
são derivados de várias 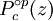 , Avaliado em
, Avaliado em  .
.
Dado  e
e  ,
,  e seus derivados pode ser avaliada por:
e seus derivados pode ser avaliada por:

 .
.
Análogo ao caso exterior, uma vez que b é encontrado, sabemos que todos os pontos dentro da distância de b / c de 4 estão dentro do grupo de Mandelbrot.
Há dois problemas práticos com a estimativa interior distância: em primeiro lugar, temos de encontrar  precisamente, e em segundo lugar, precisamos encontrar
precisamente, e em segundo lugar, precisamos encontrar  precisamente. O problema com
precisamente. O problema com  é que a convergência de
é que a convergência de  por iteração
por iteração 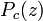 requer, teoricamente, um número infinito de operações. O problema com o período que é, por vezes, devido a erros de arredondamento, de um período é falsamente identificado para ser um múltiplo inteiro do período real (por exemplo, é detectado um período de 86, enquanto que o período real é apenas 43 = 86/2) . Nesse caso, a distância é superestimado, ou seja, o raio relatado poderia conter pontos fora do grupo de Mandelbrot.
requer, teoricamente, um número infinito de operações. O problema com o período que é, por vezes, devido a erros de arredondamento, de um período é falsamente identificado para ser um múltiplo inteiro do período real (por exemplo, é detectado um período de 86, enquanto que o período real é apenas 43 = 86/2) . Nesse caso, a distância é superestimado, ou seja, o raio relatado poderia conter pontos fora do grupo de Mandelbrot.
Otimizações
Uma forma de melhorar cálculos é saber de antemão se a dado ponto está dentro do cardióide ou no bulbo período-2.
Para evitar ter que fazer um grande número de iterações para outros pontos do conjunto, pode-se fazer a verificação "periodicidade" significa -Quais verificar se um ponto alcançado na iteração um pixel foi alcançado antes. Se assim for, o pixel não pode divergir, e deve estar no conjunto. Esta é a mais relevante para cálculos de ponto fixo, onde há uma relativamente grande chance de tal periodicidade-a cheia de ponto flutuante (ou de alta precisão) implementação raramente iria entrar em tal período.
Verificação periodicidade é, naturalmente, um trade-off: A necessidade de memorizar os aspectos custa instruções de memória e gerenciamento de dados, ao passo que ele salva instruções computacionais


![z \ mapsto \ lambda z (1-z), \ quad \ lambda \ in [1,4]. \,](../../images/214/21446.png)