Número ordinal

Representação dos números ordinais até ^ω ω. Cada volta da espiral representa um poder de ω

Na teoria dos conjuntos , um número ordinal, ou apenas ordinal, é a tipo de ordem de um bem ordenada conjunto. Ordinais são uma extensão dos números naturais diferentes de números inteiros e de cardeais . Como outros tipos de números, ordinais podem ser adicionados, multiplicaram-se, e exponenciadas. Os ordinais finitos (e os cardeais finitos) são os números naturais: 0, 1, 2, ..., uma vez que quaisquer dois ordenamentos totais de um conjunto finito são ordem isomorphic. O ordinal menos infinito é ω que é identificado com o número cardinal . Além ordinais ω no entanto (no caso transfinite) estabelecer uma distinção mais fina do que os cardeais por conta de sua informação da ordem. Considerando que há apenas um cardinal infinito contável, ou seja, em si, não são muitas uncountably ordinais infinitos contáveis, nomeadamente ω, ω + 1, ω + 2, ..., ω · 2, ω · 2 + 1, ..., ω ^2, ..., ω ^3, ..., ^ω ω, ..., ^ω ω ω, ..., ε _0, .... Aqui adição e multiplicação não são conmutativo: em particular 1 + ω é ω em vez de ω + 1, enquanto 2 · ω é ω em vez de ω · 2. O conjunto de todos os ordinais contáveis constitui o primeiro ordinal incontável ω _1, que é identificado com o cardeal (Ao lado cardinal depois ). Cardeais bem ordenadas são identificados com o seu ordinais iniciais, ou seja, a menor ordinal de que cardinalidade. A cardinalidade de um ordinal define uma associação muitos para um dos números ordinais para os cardeais.

Ordinais foram introduzidas por Georg Cantor em 1897 para acomodar sequências infinitas e classificar conjuntos com certos tipos de ordem estruturas em cima delas.

Em geral, cada α ordinal é o tipo de ordem do conjunto de ordinais estritamente menor que α si. Esta propriedade permite que cada ordinal para ser representado como o conjunto de todos os ordinais menos do que isso. Ordinais podem ser classificados como: zero, ordinais sucessores, e ordinais limite (de vária cofinalities). Dada uma classe de ordinais, pode-se identificar o membro th-α dessa classe, ou seja, um índice de lata (contar) eles. Uma classe é fechada e sem limites, se a sua função de indexação é contínuo e nunca pára. O Cantor forma normal representa com exclusividade cada ordinal como uma soma finita de poderes ordinais de ω. No entanto, isto não pode formar a base de uma notação ordinal universal devido a tais representações auto-referenciais como 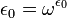. Ordinais cada vez maiores pode ser definida, mas tornam-se mais e mais difícil de descrever. Qualquer número de ordem pode ser feita em um espaço topológico, dotando-o com o ordem topologia; Esta topologia é discreto se e somente se o ordinal é um cardeal contável, ou seja, no máximo, ω. Um subconjunto de ω + 1 está aberto na topologia ordem, se e somente se, ou é cofinite ou não contém ω como um elemento.

Ordinais estender os números naturais

Um número natural (que, neste contexto, inclui o número 0 ) pode ser usada para dois fins: para descrever o tamanho de um definido, ou para descrever a posição de um elemento de uma sequência. Quando restrito a conjuntos finitos estes dois conceitos coincidem; há apenas uma maneira de colocar um conjunto finito em uma seqüência linear, a menos de isomorfismo. Ao lidar com conjuntos infinitos é preciso distinguir entre a noção de tamanho, o que leva a números cardinais , e à noção de posição, que é generalizado pelos números ordinais descritos aqui. Isto porque, enquanto qualquer conjunto tem apenas uma dimensão (a sua cardinalidade), há muitas nonisomorphic bem-ordenações de qualquer conjunto infinito, como explicado abaixo.

Considerando que a noção de número cardinal é associado a um conjunto com nenhuma estrutura especial sobre ele, os ordinais estão intimamente ligados com o tipo especial de conjuntos que são chamados bem ordenada (tão intimamente ligadas, de fato, que alguns matemáticos não fazem distinção entre os dois conceitos). Um conjunto bem ordenado é um conjunto totalmente ordenado (dadas quaisquer dois elementos um define um menor e outra maior de uma maneira coerente), no qual não há nenhuma sequência decrescente infinita (no entanto, pode haver sequências crescentes infinitas); equivalentemente, todo subconjunto não vazio do conjunto tem um elemento menos. Ordinais pode ser utilizado para rotular os elementos de qualquer dado conjunto bem ordenada (o mais pequeno elemento ser rotulado 0, após o que um 1, o próximo 2 ", e assim por diante") e para medir o "comprimento" da totalidade definir pelo menos ordinal que não é um rótulo para um elemento do conjunto. Este "comprimento" é chamado o tipo de ordem do conjunto.

Qualquer ordinal é definido pelo conjunto de ordinais que o precedem: na verdade, a definição mais comum de ordinais identifica cada ordinal como o conjunto de ordinais que o precedem. Por exemplo, o ordinal 42 é o tipo de ordem dos ordinais menos do que ele, ou seja, os ordinais de 0 (o menor de todos os ordinais) a 41 (o antecessor imediato de 42), e é geralmente identificado como o conjunto {0 , 1,2, ..., 41}. Por outro lado, qualquer conjunto de ordinais que é para baixo-closed-o que significa que qualquer ordinal menos de um ordinal no conjunto também está no set-é (ou pode ser identificado com) um ordinal.

Até agora, temos apenas mencionado ordinais finitos, que são os números naturais. Mas existem infinitos, bem como: a menor ordinal infinito é ω, que é o tipo de ordem dos números naturais (ordinais finitos) e que pode até mesmo ser identificados com o conjunto dos números naturais (na verdade, o conjunto dos números naturais é bem -ordered-como é qualquer conjunto de ordinais e uma vez que está para baixo fechada pode ser identificado com o ordinal associado a ele, que é exatamente como nós definimos ω).

Uma representação gráfica "palito" do ω² ordinal. Cada vara corresponde a um ordinal da forma ω · m + n, onde m e n são números naturais.

Talvez uma intuição mais clara dos ordinais podem ser formados por análise de um primeiro alguns deles: como mencionado acima, eles começam com os números naturais, 0, 1, 2, 3, 4, 5, ... Depois de todos os números naturais vem o primeiro ordinal infinito , ω, e depois que vêm ω + 1, + 2 ω, ω + 3, e assim por diante. (Exatamente o meio de adição será definido posteriormente em:. Apenas considerá-los como nomes) Depois de todos estes vêm ω · 2 (que é ω + ω), ω · 2 + 1, ω · 2 + 2, e assim por diante, então ω · 3 e, em seguida, mais tarde, ω · 4. Agora o conjunto de ordinais que formam deste modo (a ω · m + n, onde m e n são números naturais) em si deve ter um ordinal associado a ela, e que é ω ^2. Mais adiante, não será ω ^3, então ω ^4, e assim por diante, e ^ω ω, então ω ^ω², e muito mais tarde ε ₀ ( epsilon zero) (para dar alguns exemplos de relativamente pequeno-contável-ordinais). Nós podemos ir neste caminho longe indefinidamente ("indefinidamente longe" é exatamente o que ordinais são bons em: basicamente toda vez que alguém diz "e assim por diante" ao enumerar os ordinais, define um ordinal maior). O menor ordinal incontável é o conjunto de todos os ordinais contáveis, expressa em ω _1.

Definições

Conjuntos bem ordenados

A conjunto bem ordenado é um conjunto ordenado em que cada subconjunto não vazio tem um elemento menos: isto é equivalente (pelo menos na presença do axioma de escolha dependente) a apenas dizendo que o conjunto está totalmente ordenada e não há nenhuma sequência decrescente infinita, algo que é talvez mais fácil de visualizar. Na prática, a importância da boa ordenação é justificada pela possibilidade de aplicação indução transfinita, que diz, essencialmente, que qualquer propriedade que passa de os antecessores de um elemento para que o próprio elemento deve ser verdadeiro de todos os elementos (do dado conjunto bem-ordenado). Se os estados de uma computação (programa de computador ou um jogo) pode ser bem ordenado de tal forma que cada passo é seguido por uma etapa de "inferior", então você pode ter certeza que a computação irá terminar.

Agora nós não queremos fazer uma distinção entre dois conjuntos bem ordenados, se eles só diferem no "rotulagem dos seus elementos", ou mais formalmente: se podemos emparelhar os elementos do primeiro conjunto com os elementos do segundo conjunto, tais que se um elemento é menor do que o outro no primeiro conjunto, então o parceiro de o primeiro elemento é menor do que o parceiro de o segundo elemento do segundo conjunto, e vice-versa. Tal correspondência de um-para-um é chamado um isomorfismo ordem e os dois conjuntos bem ordenados estão a ser dito fim-isomorphic, ou similar (obviamente esta é uma relação de equivalência ). Desde que exista um isomorfismo ordem entre dois conjuntos bem ordenados, o isomorfismo ordem é único: o que torna bastante justificável considerar os conjuntos como essencialmente idêntica, e para buscar um representante "canonical" do tipo isomorfismo (classe). Este é exatamente o que os ordinais fornecer, e também fornece uma rotulagem canônica dos elementos de qualquer conjunto bem-ordenado.

Portanto, essencialmente, pretende definir um ordinal como uma classe de isomorfismo de conjuntos bem ordenados, isto é, como um classe de equivalência para a relação de equivalência de "ser fim-isomorphic". Há uma dificuldade técnica, no entanto, no facto de a classe de equivalência é demasiado grande para ser um conjunto no habitual Zermelo-Fraenkel (ZF) formalização da teoria dos conjuntos. Mas esta não é uma dificuldade séria. Vamos dizer que o ordinal é o tipo de pedido de qualquer conjunto da classe.

Definição de um ordinal como uma classe de equivalência

A definição original de número ordinal, encontrado por exemplo em Principia Mathematica, define o tipo de ordem de uma boa ordenação como o conjunto de todos bem-ordenações similares (ordem isomorphic) para que o bem-ordenação: em outras palavras, um número ordinal é genuinamente uma classe de equivalência de conjuntos bem ordenados. Esta definição deve ser abandonada em ZF e sistemas relacionados de teoria dos conjuntos axiomática , porque essas classes de equivalência são grandes demais para formar um conjunto. No entanto, esta definição pode ainda ser utilizado em teoria tipo e na teoria dos conjuntos de Quine Novas Fundações e sistemas relacionados (onde ele oferece uma solução alternativa surpreendente para o Paradoxo da maior ordinal Burali-Forti).

Von Neumann definição de ordinais

Em vez de definir um ordinal como uma classe de equivalência de conjuntos bem ordenados, vamos defini-lo como um conjunto bem-ordenado particular que (canonicamente) representa a classe. Assim, um número ordinal será um conjunto bem-ordenado; e cada conjunto bem-ordenado será fim-isomorfo a exactamente um número ordinal.

A definição padrão, sugerida por John von Neumann , é: cada ordinal é o conjunto bem-ordenado de todos os ordinais menores. Em símbolos, λ = [0, λ). Formalmente:

Um conjunto S é um ordinal se e somente se S é estritamente bem ordenada com respeito para definir a associação e cada elemento de S é também um subconjunto de S.

Note que os números naturais são ordinais por esta definição. Por exemplo, um elemento 2 é de 4 = {0, 1, 2, 3}, e 2 é igual a {0, 1} e por isso, é um subconjunto de {0, 1, 2, 3}.

Pode ser mostrado por indução transfinita que cada conjunto bem-ordenado é fim-isomorfo a exactamente um destes ordinais, isto é, há uma ordem preservação função bijective entre eles.

Além disso, os elementos de cada ordinal são próprios ordinais. Sempre que você tem dois ordinais S e T, S é um elemento de T se e somente se S é um subconjunto próprio de T. Além disso, S ou é um elemento de T, ou T é um elemento de S, ou eles são iguais. Assim, cada conjunto de ordinais é totalmente ordenado. Além disso, cada conjunto de ordinais é bem-ordenada. Este generaliza o fato de que cada conjunto de números naturais é bem ordenado.

Conseqüentemente, cada ordinal S é um conjunto tendo como elementos de forma precisa os ordinais menores do que S. Por exemplo, cada conjunto de ordinais tem um supremum, o ordinal obtido tomando a união de todos os ordinais do conjunto. Esta união existe independentemente do tamanho do conjunto, pelo axioma da união).

A classe de todos os ordinais não é um conjunto. Se fosse um jogo, pode-se mostrar que era um ordinal e, portanto, um membro de si mesmo o que contradiz a sua rigorosa ordenação por adesão. Isto é o Paradoxo Burali-Forti. A classe de todos os ordinais é variadamente chamado "Ord", "ON", ou "∞".

Um ordinal é finito se e apenas se a ordem inversa é também bem ordenada, que é o caso, se e apenas se cada uma das suas subconjuntos tem um máxima.

Outras definições

Há outras formulações modernas de a definição de ordinal. Por exemplo, assumindo que o axioma de regularidade, o seguinte são equivalentes para um conjunto x:

• x é um ordinal,
• x é um transitivo conjunto, e de filiação é definido tricotômica em x,
• x é um conjunto transitivo totalmente ordenada pelo conjunto inclusão,
• x é um conjunto transitivo de conjuntos transitivos.

Estas definições não pode ser utilizado em não-fundamentada teorias estabelecidas. Em conjunto com teorias urelements, um tem que fazer ainda mais certeza de que a definição exclui urelements de aparecer em ordinais.

Seqüência Transfinite

Se α é um ordinal limite e X é um conjunto, uma sequência indexada-α de elementos de símbolo X representa uma função de X para α. Este conceito, uma sequência ou sequência ordinal transfinito indexadas, é uma generalização do conceito de uma sequência . Uma sequência comum corresponde ao caso α = ω.

Indução Transfinite

O que é indução transfinita?

Indução Transfinite detém em qualquer conjunto bem-ordenado, mas é tão importante em relação à ordinais que vale a pena reafirmar aqui.

Qualquer propriedade que passa a partir do conjunto de ordinais menores do que um determinado α ordinal α para si, é verdade de todos os ordinais.

Isto é, se P (α) é verdadeiro sempre que P (β) é verdade para todos β <α, então P (α) é verdade para todos α. Ou, de forma mais prática: a fim de provar uma propriedade P para todos os ordinais α, pode-se supor que ele já é conhecido por todos menores β <α.

Recursão Transfinite

Transfinite indução pode ser usado, não só para provar as coisas, mas também para defini-los. Tal definição é normalmente dito ser por recursão transfinita - a prova de que o resultado é bem definida usa indução transfinita. Seja F denotar um (classe) de função F a ser definido nos ordinais. A ideia é agora que, na definição de F (α) para um α ordinal não especificado, pode-se supor que F (β) já está definido para todos β <α e, portanto, dar uma fórmula para F (α) em termos de estes F ( β). Segue-se então por indução transfinito que existe um e apenas uma função que satisfaz a fórmula de recorrência de até e incluindo α.

Aqui está um exemplo de definição de recursão transfinita sobre os ordinais (mais será dado mais tarde): definir a função F, deixando F (α) o menor ordinal não na classe {F (β) | β <α}, que é , da classe consistindo de todos os F (β) para β <α. Esta definição assume o F (β), conhecido no próprio processo de definição de F; este círculo vicioso aparente é exatamente o que por definição transfinitos licenças de recursão. Na verdade, F (0) faz sentido, uma vez que não há β ordinal <0, e a classe {F (β) | β <0} está vazio. Assim, F (0) é igual a 0 (o mais pequeno de todos ordinal). Agora que F (0) é conhecido, a definição aplica-se a F (1) faz sentido (isto é a menor não ordinal na classe Singleton {F (0)} = {0}), e assim por diante (a e assim por diante é exatamente indução transfinita). Acontece que este exemplo não é muito emocionante, uma vez que comprovadamente F (α) = α para todos os ordinais α, que podem ser mostrados, precisamente, por indução transfinita.

Sucessores e limite ordinais

Qualquer ordinal diferente de zero possui o elemento mínimo, zero. Ele pode ou não ter um elemento máximo. Por exemplo, tem 42 máximo 41 e ω + 6 tem ω máxima + 5. Por outro lado, ω não tem um máximo uma vez que não há maior número natural. Se um ordinal tem um α máximo, então é o seguinte ordinal após α, e é chamado um ordinal sucessor, ou seja, o sucessor de α, α escrito + 1. Na definição de von Neumann de ordinais, o sucessor de α é uma vez que os seus elementos são aqueles de α e α si.

Um ordinal diferente de zero que não é um sucessor é chamado de limitar ordinal. Uma das justificativas para este termo é que um ordinal limite é de fato o limite em um sentido topológico de todos os ordinais menores (sob a topologia de ordem).

Quando 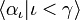é uma sequência indexada ao ordinal, indexadas por um γ limite ea seqüência está aumentando, ou seja, 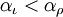sempre que definimos seu limite para ser o extremo superior do conjunto isto é, a menor ordinal (existe sempre) maior do que qualquer um dos termos da sequência. Neste sentido, um ordinal limite é o limite de todos os ordinais menores (indexados por si só). Coloque mais diretamente, é o supremo do conjunto de ordinais menores.

Outra forma de definir um limite ordinal é para dizer que é um limite α ordinal se e somente se:

Há um ordinal menos de α e ζ sempre que é menos do que um ordinal α, então existe um ordinal ξ tal que ζ <ξ <α.

Assim, na seguinte seqüência:

0, 1, 2, ..., ω, ω + 1

ω é um ordinal limite porque para qualquer ordinal (neste exemplo, um número natural), podemos encontrar outro ordinal (número natural) maior do que ele, mas ainda menos do que ω.

Assim, cada ordinal é zero, ou um sucessor (de um predecessor bem definida), ou um limite. Esta distinção é importante, porque muitas definições por indução transfinita confiar nele. Muitas vezes, ao definir uma função F por indução transfinita em todos os ordinais, define-F (0) e F (α + 1) assumindo F (α) é definida, e, em seguida, para o limite de ordinais δ define um F (δ) como o limite do F (β) para todo β <δ (seja no sentido de limites ordinais, como já foi explicado, ou por alguma outra noção de limite, se F não leva valores ordinais). Assim, o passo interessante na definição é o passo sucessor, não os ordinais limite. Essas funções (especialmente para F não-decrescente e tomando valores ordinais) são chamados contínua. Veremos que ordinal adição, multiplicação e exponenciação são contínuas em função de seu segundo argumento.

Aulas de indexação dos ordinais

Nós mencionamos que qualquer conjunto bem-ordenado é semelhante (ordem isomorphic) para um número ordinal único , Ou, em outras palavras, que os seus elementos podem ser indexados em aumentar de forma pelo menos de ordinais . Isto aplica-se, em particular, a qualquer conjunto de números ordinais: qualquer conjunto de números ordinais é naturalmente indexado pelos ordinais menos do que alguns . O mesmo se aplica, com uma ligeira modificação, para as classes de ordinais (uma coleção de números ordinais, possivelmente muito grande para formar um conjunto, definida por alguma propriedade): qualquer classe de ordinais podem ser indexados por ordinais (e, quando a classe é ilimitada na classe de todos os ordinais, este coloca-lo em classe-bijection com a classe de todos os ordinais). Assim, podemos falar livremente do 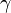ésimo elemento na classe (com a convenção de que o "0-th" é a menor, a "1-th" é a menor seguinte, e assim por diante). Formalmente, a definição é por indução transfinita: o 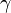ésimo elemento da classe é definida (desde que já foi definido para todos 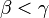), Como o elemento mais pequeno do que a maior 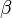ésimo elemento para todos .

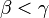Podemos aplicar esse, por exemplo, para a classe de ordinais limite: a 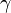ordinal -th que é ou um limite ou zero é (Veja aritmética ordinal para a definição de multiplicação de números ordinais). Da mesma forma, podemos considerar ordinais aditivamente indecomponíveis (significando um ordinal diferente de zero, que não é a soma de dois ordinais estritamente menor): A 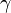-th ordinal aditiva indecomponível é indexado como 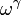. A técnica de aulas de indexação dos ordinais é frequentemente útil no contexto de pontos fixos: por exemplo, o 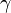ordinal -th tal que 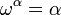está escrito 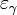. Estes são as chamadas " números epsilon ".

Conjuntos ilimitados fechados e classes

Uma classe de ordinais é dito ser ilimitada, ou Cofiñal, quando dada qualquer ordinal, há sempre algum elemento da classe maior do que ele (a classe, em seguida, deve ser uma classe adequada, isto é, não pode ser um conjunto). 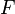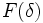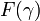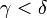Diz-se a ser fechado, quando o limite de uma sequência de ordinais na classe é novamente na classe: ou, de forma equivalente, quando a função de indexação (classe) é contínua no sentido de que, para um ordinal limite, (O ordinal -th na classe) é o limite de tudo para ; este também é o mesmo que ser fechada, no sentido topológico, para o topologia de ordem (para evitar falar de topologia em classes próprias, pode-se exigir que a interseção da classe com qualquer ordinal está fechado para a topologia de pedido no que ordinal, este é novamente equivalente).

De particular importância são as categorias de ordinais que são fechada e sem limites, às vezes chamado de clubes. Por exemplo, a classe de todos os ordinais limite é fechada e sem limites: isso se traduz o fato de que há sempre um ordinal limite maior que um determinado ordinal, e que um limite de ordinais limite é um limite ordinal (um fato feliz se a terminologia é de fazer qualquer sentido em tudo!). A classe de ordinais aditiva indecomponíveis, ou a classe de ordinais, ou a classe dos cardeais , estão todos fechados sem limites; o conjunto de regulares cardeais, no entanto, é ilimitado, mas não fechado, e qualquer conjunto finito de números ordinais é fechado, mas não ilimitado.

Uma classe é imobilizado se tem uma interseção não vazia com cada classe ilimitada fechado. Todos os superclasses de aulas ilimitadas fechados são classes estacionários e estacionários são ilimitadas, mas há aulas fixas que não estão fechados e há aulas fixas que não têm subclasse ilimitada fechado (como a classe de todos os ordinais limite com cofinality contável). Desde a interseção de duas classes ilimitados fechados é fechada e sem limites, a intersecção de uma classe estacionária e uma classe ilimitada fechado é estacionária. Mas a intersecção de duas classes estacionárias pode estar vazio, por exemplo, a classe de ordinais com ω cofinality com a classe de ordinais com cofinality incontável.

Em vez de formular essas definições para classes (próprios) de ordinais, podemos formulá-las para conjuntos de números ordinais abaixo de um dado ordinal : Um subconjunto de um limite ordinal é dito ser ilimitada (ou Cofiñal) sob desde menos do que qualquer ordinal é inferior a alguns ordinal no conjunto. De modo mais geral, podemos chamar um subconjunto de qualquer ordinal Cofiñal em fornecida a cada ordinal menos de é menor do que ou igual a alguns ordinal no conjunto. O subconjunto é dito para ser fechada sob desde que seja fechado para o fim em topologia , Ou seja, um limite de ordinais no conjunto seja no conjunto ou igual a si.

Aritmética dos ordinais

Há três operações habituais sobre ordinais: adição, multiplicação e (ordinal) exponenciação. Cada um pode ser definido em essencialmente duas maneiras: ou através da construção de um conjunto bem-ordenado explícito que representa a operação ou usando recursão transfinita. Cantor forma normal fornece uma maneira padronizada de escrever ordinais. Os chamados "naturais" operações aritméticas reter commutativity à custa de continuidade.

Ordinais e cardinais

Ordinal inicial de um cardeal

Cada ordinal tem um associado cardeal , sua cardinalidade, obtido por simplesmente esquecer o fim. Qualquer conjunto bem-ordenado ter que ordinal como seu tipo de ordem tem a mesma cardinalidade. O menor ordinal ter um determinado cardeal como sua cardinalidade é chamado de ordinal inicial daquele cardeal. Cada ordinal finito (número natural) é inicial, mas a maioria dos ordinais infinitos não são inicial. O axioma da escolha é equivalente à afirmação de que cada jogo pode ser bem ordenada, ou seja, que cada cardeal tem um ordinal inicial. Neste caso, é tradicional para identificar o número cardinal com o seu ordinal inicial, e dizemos que o ordinal inicial é de um cardeal.

O ordinal inicial infinito th-α está escrito 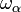. A sua cardinalidade é escrito . Por exemplo, a cardinalidade de ω ₀ = ω é , Que também é a cardinalidade de ω² ou ε ₀ (todos são ordinais contáveis). Então, (assumindo que o axioma da escolha) nos identificamos com ω , Excepto que a notação é usado quando se escreve cardeais, e ω ao escrever ordinais (isto é importante, uma vez 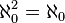enquanto que 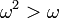). Além disso, 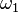é o menor ordinal incontável (para ver que ele existe, considere o conjunto de classes de equivalência de bem-ordenações dos números naturais: cada um desses bem-ordenação define um ordinal contável, e 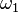é o tipo de ordem desse conjunto), 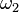é o menor ordinal cuja cardinalidade é maior do que , E assim por diante, e 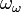é o limite do para números naturais n (qualquer limite de cardeais é um cardeal, então esse limite é de fato o primeiro cardeal depois de todo o ).

Veja também Von Neumann atribuição cardeal.

Cofinality

O cofinality de um ordinal é o menor ordinal o qual é o tipo de pedido de um subconjunto de Cofiñal . Observe que um número de autores definem confinality ou usá-lo apenas para ordinais limite. O cofinality de um conjunto de ordinais ou qualquer outro conjunto bem ordenado é o cofinality do tipo de ordem desse conjunto.

Assim, para um ordinal limite, existe um indexados estritamente crescente seqüência com limite . Por exemplo, o cofinality de ω² é ω, porque a sequência de ω · m (em que m varia ao longo dos números naturais) tende a ω²; mas, de modo mais geral, qualquer limite ordinal contável tem cofinality ω. Um limite ordinal incontável pode ter ou cofinality ω como faz 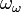ou um cofinality incontável.

O cofinality de 0 é 0. E o cofinality de qualquer ordinal sucessor é 1. O cofinality de qualquer limite ordinal é, pelo menos, .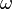

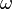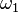Um ordinal que é igual ao seu cofinality é chamado regular e é sempre um ordinal inicial. Qualquer limite de ordinais regulares é um limite de ordinais iniciais e, portanto, também é inicial, mesmo se não for regular, que geralmente não é. Se o Axioma da Escolha, em seguida, é regular para cada α. Neste caso, os ordinais 0, 1, , E 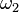são regulares, ao passo que 2, 3, 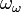E _ω ω _{· 2} são ordinais iniciais que não são regulares.

O cofinality de qualquer α ordinal é um ordinal regular, isto é, a cofinality do cofinality de α é o mesmo que o cofinality de α. Assim, a operação é cofinality idempotent.

Alguns "grandes" ordinais contáveis

Nós já mencionamos (ver Cantor forma normal) a ε ordinal _0, que é o mais pequeno que satisfaz a equação 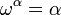, Por isso, é o limite da sequência de 0, 1, 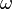, , 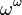, Etc. Muitas ordinais pode ser definida de tal maneira como pontos fixos de certas funções ordinais (a ordinal -ésimo tal que 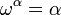é chamado 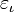, Então poderíamos ir na tentativa de encontrar o ordinal -ésimo tal que 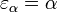", E assim por diante", mas toda a sutileza reside no "e assim por diante"). Podemos tentar fazer isso de forma sistemática, mas não importa que sistema é usado para definir e construir ordinais, há sempre um ordinal que se encontra logo acima de todos os ordinais construídos pelo sistema. Talvez o ordinal mais importante que limita desta maneira um sistema de construção é o Church- Kleene ordinal, 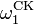(Apesar do 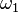no nome, este ordinal é contável), que é o menor ordinal que não pode de forma alguma ser representado por um função computável (isso pode ser feito rigorosa, é claro). Consideravelmente grandes ordinais pode ser definido abaixo 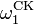, No entanto, que medem a "força-prova teórica" de certos sistemas formais (por exemplo, 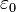mede a força Aritmética de Peano). Grandes ordinais também pode ser definido acima do ordinal Igreja-Kleene, que são de interesse em várias partes da lógica.

Topologia e ordinais

Qualquer ordinal pode ser feita em um espaço topológico de uma forma natural, dotando-o com o topologia de ordem. Veja a Seção Topologia e ordinais do artigo "topologia Order".

Downward conjuntos fechados de ordinais

Um conjunto é descendente fechado se nada menos do que um elemento do conjunto também está no conjunto. Se um conjunto de ordinais é descendente fechados, então esse conjunto é um ordinal-o menos, não ordinal no conjunto.

Exemplos:

• O conjunto de ordinais menos do que 3 é 3 = {0, 1, 2}, a menor ordinal não menos do que 3.
• O conjunto de ordinais finitos é infinito, o menor ordinal infinito: ω.
• O conjunto de ordinais contáveis é incontável, a menor ordinal incontável: ω _1.