
Trigonometria
Sobre este escolas selecção Wikipedia
Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. SOS Children trabalha em 45 países africanos; você pode ajudar uma criança em África ?

| Trigonometria |
|---|
| História Uso Funções Generalized Funções inversas Outras leituras |
| Referência |
| Identidades Constantes exatas Tabelas trigonométricas |
| Leis e teoremas |
| Lei de senos Lei dos cossenos Lei das tangentes Lei de cotangentes Teorema de Pitágoras |
| Cálculo |
| Substituição trigonométrica Integrais de funções Derivados de funções Integrais de funções inversas |
Trigonometria (a partir de grego trigōnon "triângulo" + metron "medida") é um ramo da matemática que estuda triângulos e as relações entre os comprimentos de seus lados e os ângulos entre esses lados. Trigonometria define as funções trigonométricas , que descrevem essas relações e têm aplicabilidade aos fenômenos cíclicos, tais como ondas. O campo evoluiu durante o século III aC como um ramo da geometria usada extensivamente para estudos astronômicos. É também a base da prática da arte agrimensura.
Noções básicas de trigonometria são frequentemente ensinada nas escolas , quer como um curso separado ou como parte de um curso pré-cálculo. As funções trigonométricas estão presentes em partes do matemática pura e matemática aplicada , tais como E a análise de Fourier equação de onda, o que por sua vez são essenciais para muitos ramos da ciência e da tecnologia. Esféricas estudos trigonometria triângulos em esferas , superfícies de constante positiva curvatura, em geometria elíptica. É fundamental para a astronomia e navegação. Trigonometria em superfícies de curvatura negativa é parte de Geometria hiperbólica.
História

Sumérios astrônomos introduziu medida do ângulo, usando uma divisão de círculos em 360 graus. Eles e seus sucessores os babilônios estudou as relações dos lados de triângulos semelhantes e descobriu algumas propriedades destes rácios, mas não transformar isso em um método sistemático para encontrar os lados e ângulos de triângulos. O Nubians antigo usou um método semelhante. Os antigos gregos transformado trigonometria em uma ciência ordenada.
Clássico Matemáticos gregos (tais como Euclides e Arquimedes ) estudaram as propriedades de acordes e ângulos inscritos em círculos, e provou teoremas que são equivalentes a fórmulas trigonométricas modernos, apesar de apresentarem-los geometricamente em vez de algebricamente. Cláudio Ptolomeu expandida Chords Hiparco em um círculo em sua Almagesto. O moderno função seno foi definida pela primeira vez no Surya Siddhanta, e suas propriedades foram ainda documentadas pelo 5o século matemático indiano e astrônomo Aryabhata. Estas obras gregas e indianas foram traduzidos e expandiu-se matemáticos islâmicos medievais. Por volta do século 10, os matemáticos islâmicos estavam usando todas as seis funções trigonométricas, tinha tabulados seus valores, e foram aplicá-los a problemas em geometria esférica. Mais ou menos ao mesmo tempo, Matemáticos chineses desenvolveram trigonometria de forma independente, embora não tenha sido um grande campo de estudo para eles. Conhecimento de funções trigonométricas e métodos chegou à Europa via Traduções latinas das obras de Astrónomos persas e árabes, como Al Battani e Nasir al-Din al-Tusi. Um dos primeiros trabalhos sobre trigonometria por um matemático europeu é De triangulis por volta do século 15 alemão matemático Regiomontanus. Trigonometria foi ainda tão pouco conhecido na Europa do século 16 que Nicolaus Copernicus dedicou dois capítulos de De Revolutionibus Orbium Coelestium para explicar seus conceitos básicos.
Impulsionada pelas exigências da navegação e à crescente necessidade de mapas precisos de grandes áreas, trigonometria cresceu em um importante ramo da matemática. Bartholomaeus Pitiscus foi o primeiro a usar a palavra, a publicação de sua Trigonometria em 1595. Gemma Frisius descrito pela primeira vez que o método de triangulação ainda hoje utilizada no levantamento. Foi Leonhard Euler que totalmente incorporada números complexos em trigonometria. As obras de James Gregory no século 17 e Colin Maclaurin no século 18 foram influentes no desenvolvimento de séries trigonométricas. Também no século 18, Brook Taylor definido o general série de Taylor .
Visão global

Se um ângulo de um triângulo é de 90 graus e um dos outros ângulos é conhecido, o terceiro é assim fixado, porque os três ângulos de qualquer triângulo adicionar até 180 graus. Os dois ângulos agudos, portanto, adicionar até 90 graus: eles são ângulos complementares. O forma de um triângulo é completamente determinada, excepto semelhança, por os ângulos. Uma vez que os ângulos são conhecidos, o rácios dos lados são determinados, independentemente do tamanho total do triângulo. Se o comprimento de um dos lados é conhecido, os outros dois são determinados. Estas proporções são dadas pelos seguintes funções trigonométricas do ângulo A conhecido, onde a, b e c referem-se os comprimentos dos lados na figura anexa:
- Função seno (sin), definida como a relação do lado oposto ao ângulo ao hipotenusa.
- Cosseno função (COS), definido como a razão entre o perna adjacente à hipotenusa.
- Tangente função (TAN), definido como a razão entre a perna oposta ao segmento adjacente.
A hipotenusa é o lado oposto ao ângulo de 90 graus em um triângulo retângulo; isto é o lado mais comprido do triângulo, e um dos dois lados adjacentes ao ângulo A. A perna é adjacente do outro lado que é adjacente ao ângulo A. O lado oposto é o lado que é oposto ao ângulo A. Os termos perpendiculares e base são por vezes utilizados para os lados opostos e adjacentes respectivamente. Muitos falantes de inglês encontrá-lo fácil de lembrar o que os lados do triângulo retângulo são iguais para seno, cosseno, tangente ou, memorizando a palavra-SOH CAH-TOA (veja abaixo sob Mnemonics ).
O recíprocos destas funções são nomeados a co-secante (csc ou cosec), secante (seg), e co-tangente (berço), respectivamente:
O funções inversas são chamados o arco-seno, arco cosseno e arco tangente, respectivamente. Existem relações aritméticas entre estas funções, que são conhecidos como identidades trigonométricas. O co-seno, co-tangente, e co-secante são assim chamados porque eles são, respectivamente, o seno, tangente, secante e do ângulo complementar abreviado para "co-".
Com estas funções pode-se responder a praticamente todas as perguntas sobre triângulos arbitrários usando o lei de senos e do lei dos cossenos. Essas leis podem ser usados para calcular os restantes ângulos e lados de qualquer triângulo, logo que dois lados e seu ângulo incluído ou dois ângulos e um lado ou três lados são conhecidos. Essas leis são úteis em todos os ramos da geometria, uma vez que cada polígono pode ser descrito como uma combinação finita de triângulos.
Estendendo as definições

As definições anteriores aplicam-se aos ângulos entre 0 e 90 graus (0 e π / 2 radianos ) apenas. Usando o círculo unitário, pode estendê-las a todos os argumentos positivos e negativos (veja função trigonométrica ). As funções trigonométricas são periódica, com um período de 360 graus ou 2π radianos. Isso significa que os seus valores se repetiu a esses intervalos. As funções tangente e cotangente também têm um período mais curto, de 180 graus ou π radianos.
As funções trigonométricas pode ser definida de outros modos para além das definições acima geométricas, utilizando ferramentas de cálculo e série infinita. Com estas definições das funções trigonométricas pode ser definido por números complexos . A função exponencial complexa é particularmente útil.
Ver Euler e Fórmulas de Moivre.

Processo de representação gráfica de y = sin (x), utilizando um círculo unitário.

Processo de representação gráfica de y = tan (x) usando um círculo unitário.

Processo de representação gráfica de y = csc (x) usando um círculo unitário.
Mnemônica
Um uso comum do mnemônicos é se lembrar de fatos e relações em trigonometria. Por exemplo, as seno, cosseno, tangente e proporções em um triângulo retângulo pode ser lembrado por eles representam como sequências de letras. Por exemplo, um mnemônico para falantes de inglês é SOH-CAH-TOA:
- S ine = O pposite ÷ H ypotenuse
- C = Uma osine H ypotenuse djacent ÷
- T = O angent pposite ÷ A djacent
Uma maneira de lembrar as letras é a soar-los foneticamente (ou seja, SOH-CAH-TOA, que se pronuncia 'de reboque o-kə-' Uh '). Outro método consiste em expandir as letras em uma frase, como "S ome O ld H ippy C aught Um nother H ippy T rippin 'O n A cid".
Calculando funções trigonométricas
Funções trigonométricas estavam entre os primeiros usos para tabelas matemáticas. Essas tabelas foram incorporados em livros didáticos de matemática e os estudantes foram ensinados a olhar para cima os valores e como interpolar entre os valores listados para obter maior precisão. As réguas de cálculo teve escalas especiais para funções trigonométricas.
Hoje calculadoras científicas têm botões de cálculo dos principais funções trigonométricas (sin, cos, tan, e às vezes cis e suas inversas. A maioria permite uma escolha de métodos de medição angular: graus, radianos e, às vezes, grad. A maioria computador linguagens de programação fornecem bibliotecas de funções, que incluem as funções trigonométricas. O hardware unidade de ponto incorporados nos microprocessadores usados na maioria dos computadores pessoais têm instruções internas para o cálculo de funções trigonométricas flutuante.
Aplicações da trigonometria

Há um número enorme de usos de trigonometria e funções trigonométricas. Por exemplo, a técnica de triangulação é usado na astronomia para medir a distância às estrelas mais próximas, em geografia para medir distâncias entre os pontos de referência e, sistemas de navegação por satélite. As funções seno e cosseno são fundamentais para a teoria da funções periódicas, tais como aquelas que descrevem som e luz ondas.
Os campos que usam funções de trigonometria ou trigonométricas incluem astronomia (especialmente para a localização de posições aparentes de objetos celestes, em que a trigonometria esférica é essencial) e, portanto, navegação (sobre os oceanos, em aviões, e no espaço), teoria musical, acústica, óptica , a análise dos mercados financeiro, de eletrônicos , a teoria da probabilidade , estatística , biologia , imagiologia médica ( CAT scans e ultra-som), farmácia, química , teoria dos números (e, portanto, criptologia ), sismologia, meteorologia , oceanografia , muitas ciências físicas , terra levantamento e geodésia, arquitetura , fonética, economia , engenharia elétrica , engenharia mecânica , engenharia civil , gráficos de computador, cartografia, e cristalografia desenvolvimento de jogos.
Identidades padrão
As identidades são essas equações que são verdadeiras para qualquer valor.
Fórmulas de transformação de Ângulo
Fórmulas comuns

Certos equações envolvendo funções trigonométricas são verdadeiras para todos os ângulos e são conhecidos como identidades trigonométricas. Algumas identidades equacionar uma expressão para uma expressão diferente, envolvendo os mesmos ângulos. Estes estão listados em Lista de identidades trigonométricas. Identidades triângulo que se relacionam com os lados e ângulos de um triângulo dado estão listados abaixo.
Nos seguintes identidades, A, B e C são os ângulos de um triângulo e a, b e c são os comprimentos dos lados do triângulo em frente aos respectivos ângulos.
Lei de senos
O lei dos senos (também conhecida como a "regra sine") para um arbitrárias estados triângulo:
em que R é o raio do círculo circunscrito do triângulo:
Outra lei envolvendo senos pode ser usado para calcular a área de um triângulo. Dados dois lados e o ângulo entre os lados, a área do triângulo é:

Lei dos cossenos
O lei dos cossenos (conhecida como a fórmula do cosseno, ou a "regra cos") é uma extensão do teorema de Pitágoras para triângulos arbitrários:
ou de modo equivalente:
Lei das tangentes
O lei de tangentes:
A fórmula de Euler
A fórmula de Euler, que afirma que  , Produz os seguintes analíticos identidades para seno, cosseno, tangente e em termos de e e a unidade imaginária i:
, Produz os seguintes analíticos identidades para seno, cosseno, tangente e em termos de e e a unidade imaginária i:
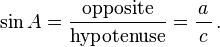

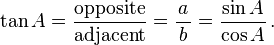


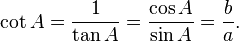
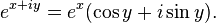


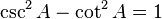


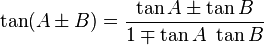
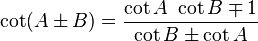
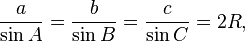


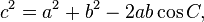

![\ Frac {ab} {a + b} = \ frac {\ tan \ left [\ tfrac {1} {2} (AB) \ right]} {\ tan \ left [\ tfrac {1} {2} (A + B) \ right]}](../../images/2161/216156.png)

