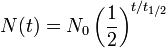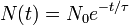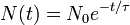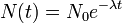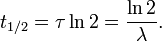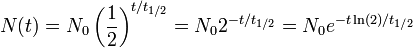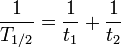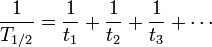Meia-vida

Assuntos Relacionados: Física

Fundo para as escolas Wikipédia

Os artigos desta seleção Escolas foram organizados por tópico currículo graças a voluntários Crianças SOS. SOS Children é a maior doação de caridade do mundo órfãos e crianças abandonadas a chance da vida familiar.

Número de semividas decorrido	Fração remanescente	Percentagem remanescente
0	_^1/1	100
1	_^1/2	50
2	_^1/4	25
3	_^1/8	12	.5
4	_^1/16	6	.25
5	_^1/32	3	0,125
6	_^1/64	1	0,563
7	_^1/128	0	0,781
...	...	...
n	_{^{1/2 n}}	100 / (2 ^N)

Meia-vida (t _meia) é o tempo necessário para uma quantidade a cair para metade do seu valor como medido no início do período de tempo. Na física, é tipicamente utilizada para descrever uma propriedade de decaimento radioactivo, mas pode ser utilizado para descrever qualquer quantidade que segue um decaimento exponencial.

O termo original, datado de Ernest Rutherford descoberta do princípio 's em 1907, foi "período de meia-vida", que foi encurtado para "meia-vida" no início de 1950.

Meia-vida é usado para descrever uma quantidade de sofrer decaimento exponencial, e é constante ao longo do tempo de vida da quantidade de deterioração. É um unidade característica para a equação de decaimento exponencial. O termo "meia-vida" pode ser utilizado genericamente para referir-se a qualquer período de tempo em que uma quantidade cai para metade, até mesmo se não é o decaimento exponencial. Para uma introdução geral e descrição do decaimento exponencial, consulte decaimento exponencial. Para uma introdução geral e descrição de decadência não-exponencial, consulte lei de velocidade.

O inverso de meia-vida é tempo de duplicação.

O quadro à direita mostra a redução de uma quantidade em termos do número de semi-vidas decorridos.

Natureza probabilística de meia-vida

Simulação de muitos átomos idênticos de sofrer decaimento radioativo, começando com qualquer 4 átomos por caixa (à esquerda) ou 400 (à direita). O número no topo é quantas meias-vidas se passaram. Note-se a lei dos grandes números: Com mais átomos, a decadência global é mais regular e mais previsível.

A meia-vida geralmente descreve a decomposição de entidades discretas, tais como átomos radioactivos, que têm núcleos instáveis. Nesse caso, ele não funciona para usar a definição de "meia-vida é o tempo necessário para exatamente a metade das entidades da corrupção". Por exemplo, se houver apenas um átomo radioactivo com uma semi-vida de um segundo, não haverá "uma-metade de um átomo" deixado após um segundo. Não vai ser zero átomos de esquerda ou um átomo de esquerda, dependendo se ou não esse átomo aconteceu a decadência.

Em vez disso, a semi-vida é definido em termos de probabilidade . É o momento em que o valor esperado do número de entidades que se decomposto é igual a metade do número original. Por exemplo, pode-se começar com um único átomo radioativo, espere sua meia-vida, e depois verificar se é ou não decaiu. Talvez ele fez, mas talvez isso não aconteceu. Mas, se esta experiência é repetida uma e outra vez, será visto que - em média - decai no interior da meia-vida de 50% do tempo.

Em algumas experiências (tais como a síntese de um elemento superheavy), não é, de facto, apenas um átomo radioactivo produzido de cada vez, com o seu tempo de vida medidos individualmente. Neste caso, a análise estatística é necessária para inferir a meia-vida. Em outros casos, um número muito grande de átomos idênticos decaimento radioactivo no intervalo de tempo medido. Neste caso, o lei dos grandes números assegura que o número de átomos de decaimento que, na verdade, é aproximadamente igual ao número de átomos que se prevê venham a decair. Em outras palavras, com um grande número suficiente de átomos de decomposição, os aspectos probabilísticos do processo poderia ser negligenciada.

Existem vários exercícios simples que demonstram deterioração probabilística, por exemplo envolvendo lançando moedas ou executando uma estatística programa de computador. Por exemplo, a imagem à direita é uma simulação de muitos átomos idênticos submetidos decaimento radioativo. Note-se que depois de uma semi-vida não são exactamente metade dos átomos restantes, apenas cerca de, por causa da variação aleatória no processo. No entanto, com mais átomos (caixas direita), a deterioração geral é mais suave e menos aleatório aparência do que com menos átomos (caixas à esquerda), de acordo com o lei dos grandes números.

Fórmulas para meia-vida no decaimento exponencial

Um processo de decaimento exponencial pode ser descrito por qualquer uma das seguintes três fórmulas equivalentes:

$N (t) = N_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}}$

$N (t) = N_0 e ^ {- t / \ tau} \,$

$N (t) = N_0 e ^ {- \ lambda t} \,$

onde

N ₀ é a quantidade inicial da substância que irá decair (esta quantidade pode ser medida em gramas, moles, o número de átomos, etc),
N (t) é a quantidade que permanece e que ainda não tenha deteriorado após um tempo t,
t _1/2 representa a semivida da quantidade de deterioração,
τ é um número positivo denominado tempo de vida do quantidade de deterioração dizer,
λ é um número positivo denominado constante de decaimento da quantidade de deterioração.

Os três parâmetros 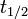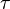$t_ {1/2}$ , $\ Tau$ E λ são todos diretamente relacionados da seguinte maneira:

$t_ {1/2} = \ frac {\ ln (2)} {\ lambda} = \ tau \ ln (2)$

onde ln (2) é o logaritmo natural de 2 (cerca de 0,693).

Clique "show" para ver uma derivação detalhada da relação entre a meia-vida, tempo de decaimento, e constante decadência.

Comece com as três equações

$N (t) = N_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}}$

$N (t) = N_0 e ^ {- t / \ tau}$

$N (t) = N_0 e ^ {- \ lambda t}$

Queremos encontrar uma relação entre 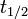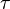$t_ {1/2}$ , $\ Tau$ , E λ, de tal forma que estas três equações descrever exactamente o mesmo processo de decaimento exponencial. Comparando as equações, encontramos a seguinte condição:

$\ Left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} = e ^ {- t / \ tau} = e ^ {- \ lambda t}$

A seguir, vamos tomar o logaritmo natural de cada uma dessas quantidades.

$\ Ln \ left (\ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} \ right) = \ ln (e ^ {- t / \ tau}) = \ ln (e ^ {- \ lambda t})$

Usando as propriedades de logaritmos, isso simplifica o seguinte:

$(T / t_ {1/2}) \ ln \ left (\ frac {1} {2} \ right) = (-t / \ tau) \ ln (e) = (- \ lambda t) \ ln (e )$

Desde o logaritmo natural e é 1, temos:

$(T / t_ {1/2}) \ ln \ left (\ frac {1} {2} \ right) = -t / \ tau = - \ lambda t$

Cancelando o fator de t e conectar $\ Ln \ left (\ frac {1} {2} \ right) = - \ ln 2$ , O eventual resultado é:

$t_ {1/2} = \ tau \ ln 2 = \ frac {\ ln 2} {\ lambda}.$

Ao ligar e manipular essas relações, temos todas as seguintes descrições equivalentes de decaimento exponencial, em termos da meia-vida:

$N (t) = N_0 \ left (\ frac {1} {2} \ right) ^ {t / t_ {1/2}} = N_0 2 ^ {- t / t_ {1/2}} = N_0 e ^ {-t \ ln (2) / T_ {1/2}}$

$T_ {1/2} = t / \ log_2 (N_0 / N (t)) = T / (\ log_2 (N_0) - \ log_2 (N (t))) = (\ log_ {2} ^ t (N_0 / N (t))) ^ {- 1} = t \ ln (2) / \ ln (N_0 / N (t))$

Independentemente da forma como está escrito, podemos ligar para a fórmula para obter

$N (0) = N_0$ como se esperava (isto é, a definição de "quantidade inicial")
$N (t_ {1/2}) = \ left (\ frac {1} {2} \ right) N_0$ como se esperava (isto é a definição de uma meia-vida)
$\ Lim_ {t \ a \ infty} N (t) = 0$ , Ou seja, montante se aproxima de zero quando t tende a infinito como esperado (quanto mais esperarmos, é menos certo).

Decay por dois ou mais processos

Alguns quantidades decadência por dois processos de decaimento exponencial-simultaneamente. Neste caso, o real t uma meia-vida _{de 1/2} pode estar relacionada com a semi-vida t ₁ e t _2, que a quantidade teriam se cada um dos processos de deterioração actuado isoladamente:

$\ Frac {1} {{T_ 1/2}} = \ frac {1} {} t_1 + \ frac {1} {} T_2$

Para três ou mais processos, a fórmula é análoga:

$\ frac {1} {t_ {1/2}} = \ frac {1} {} T_1 + \ frac {1} {} T_2 + \ frac {1} {t_3} + \ cdots$

Para uma prova destas fórmulas, ver Decay por dois ou mais processos.

Exemplos

Há uma meia-vida de descrever qualquer processo exponencial-decadência. Por exemplo:

A corrente que flui através de um Circuito RC ou Circuito RL decai com uma meia-vida de 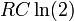$RC \ ln (2)$ ou $\ Ln (2) L / R$ , Respectivamente. Para este exemplo, o termo metade do tempo pode ser utilizado em vez de "meia vida", mas eles querem dizer a mesma coisa.
Numa primeira ordem de reacção química , a semi-vida do reagente é $\ Ln (2) / \ lambda$ , Onde λ é a velocidade de reacção constante.
Em decaimento radioactivo, a semi-vida é o período de tempo após o qual existe uma probabilidade de 50% que um átomo terá sofrido nuclear deterioração. Ela varia dependendo do tipo e átomo de isótopo , e é geralmente determinada experimentalmente. Ver Lista de nuclidos.

a meia-vida de uma espécie é o tempo que leva para a concentração da substância a cair para metade do seu valor inicial

Meia-vida em decadência não-exponencial

O decaimento de muitas grandezas físicas não é exemplo para-exponencial, a evaporação de água a partir de uma poça, ou (frequentemente) a reacção química de uma molécula. Em tais casos, a semi-vida é definido da mesma maneira como antes: como o tempo decorrido antes de metade da quantidade inicial decaiu. No entanto, ao contrário de um decaimento exponencial, a semi-vida depende da quantidade inicial, e a meia-vida em perspectiva vai mudar ao longo do tempo como a quantidade decai.

Como um exemplo, o decaimento radioactivo de carbono-14 é exponencial com uma semi-vida de 5730 anos. A quantidade de carbono-14 irá decair para metade do seu valor original ( em média ) depois de 5.730 anos, independentemente de quão grande ou pequena a quantidade original. Depois de mais 5.730 anos, de um quarto do original permanecerá. Por outro lado, o tempo que levará uma poça de meia-evaporar depende de quão profunda é a poça. Talvez uma poça de uma determinada dimensão irá evaporar-se até metade do seu volume original em um dia. Mas, no segundo dia, não existe razão para esperar que um quarto da poça permanecerá; na verdade, ele provavelmente será muito menos do que isso. Este é um exemplo em que a semi-vida diminuiu à medida que o tempo passa. (Em outras decaimentos não-exponencial, pode aumentar em vez disso.)

O decaimento de uma mistura de dois ou mais materiais que cada decaimento exponencial, mas com diferentes tempos de semi-vida, não é exponencial. Matematicamente, a soma das duas funções exponenciais não é uma única função exponencial. Um exemplo comum de tal situação é o desperdício de centrais nucleares, que é uma mistura de substâncias com muito diferentes semi-vidas. Considere-se uma amostra contendo um elemento de rápida decomposição A, com uma semi-vida de 1 segundo, e um elemento lentamente decomposição B, com uma meia-vida de um ano. Após alguns segundos, quase todos os átomos do elemento A decaíram após redução para metade repetida do número total de átomos inicial; mas muito poucos dos átomos do elemento B terá ainda deteriorado como apenas uma pequena fração de uma meia-vida tenha decorrido. Assim, a mistura considerada como um todo não deteriorar por metades.

Meia-vida na biologia e farmacologia

A meia-vida biológica ou meia-vida de eliminação é o tempo que leva para que uma substância (droga, nuclido radioactivo, ou outra) para perder metade do seu farmacológico, fisiológico, ou actividade radiológica. Num contexto clínico, a meia-vida pode também descrever o tempo que leva para a concentração em plasma sanguíneo de uma substância para atingir metade do seu valor de estado estável (a "semi-vida no plasma").

A relação entre os biológicos e tempo de semi-vida de uma substância pode ser complexo, devido a factores que incluem a acumulação de tecidos, Ativo metabolitos, e interacções do receptor.

Enquanto um isótopo radioactivo decai quase perfeitamente de acordo com os chamados "cinética de primeira ordem", onde a constante de velocidade é um número fixo, a eliminação de uma substância a partir de um organismo vivo geralmente segue a cinética químicos mais complexos.

Por exemplo, a semi-vida biológica da água em um ser humano é de cerca de 7 a 14 dias, embora este possa ser alterado pelo seu / sua comportamento. A meia-vida biológica de césio em seres humanos situa-se entre um a quatro meses. Este pode ser encurtado através da alimentação da pessoa Azul da Prússia, que actua como um sólido permutador de iões que absorve o césio, enquanto libera potássio íons em seu lugar.

Retirado de " http://en.wikipedia.org/w/index.php?title=Half-life&oldid=550971959 "

Home Page - YouTube Channel