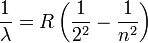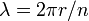Introdução à mecânica quântica
Você sabia ...
Crianças SOS voluntários ajudaram a escolher artigos e fez outro material currículo Antes de decidir sobre o patrocínio de uma criança, por que não aprender sobre as diferentes instituições de caridade de patrocínio primeiro ?
| Mecânica quântica |
|---|
 Dualidade onda-partícula |
| Introdução Glossário · História |
Fundo
|
Conceitos fundamentais
|
Experiências
|
Formulações
|
Equações
|
Interpretações
|
Tópicos avançados
|
Os cientistas
|

A mecânica quântica (MQ, ou teoria quântica) é uma ciência física lidar com o comportamento da matéria e da energia na escala de átomos e subatômicas partículas / ondas . QM também constitui a base para o entendimento contemporâneo de como objetos muito grandes, tais como estrelas e galáxias , e cosmológicos eventos como o Big Bang, podem ser analisados e explicados. A mecânica quântica é a base de várias disciplinas conexas, incluindo nanotecnologia, física da matéria condensada , química quântica , biologia estrutural, física de partículas , e eletrônica .
O termo "mecânica quântica" foi cunhado pela primeira vez por Max Born em 1924. A aceitação pela comunidade física geral da mecânica quântica é devido à sua previsão precisa do comportamento físico de sistemas, incluindo sistemas em que a mecânica newtoniana falha. Mesmo relatividade geral é limitada de forma a mecânica quântica é não-para descrever sistemas em escala atômica ou menor, a muito baixas ou muito altas energias, ou com as mais baixas temperaturas. Através de um século de experimentação e de ciência aplicada, a teoria da mecânica quântica tem provado ser muito bem sucedido e prático.
Visão global
Os fundamentos da mecânica quântica datam do início dos anos 1800, mas os começos reais da data QM do trabalho de Max Planck em 1900. Albert Einstein e Niels Bohr em breve fez importantes contribuições para o que hoje é chamado de "teoria quântica de idade." No entanto, não foi até 1924 que uma imagem mais completa surgiu com Louis de Broglie de hipótese de onda matéria e a verdadeira importância da mecânica quântica tornou-se claro. Alguns dos mais proeminentes cientistas de contribuir, posteriormente, em meados de 1920 para o que hoje é chamado de "nova mecânica quântica" ou "nova física" foram Max Born, Paul Dirac , Werner Heisenberg, Wolfgang Pauli, e Erwin Schrödinger. Mais tarde, o campo foi expandida com o trabalho por Julian Schwinger, Sin-Itiro Tomonaga e Richard Feynman para o desenvolvimento de Eletrodinâmica Quântica em 1947 e por Murray Gell-Mann, em particular, para o desenvolvimento de Cromodinâmica quântica.

Os primeiros pesquisadores diferem em suas explicações sobre a natureza fundamental do que hoje chamamos de radiação eletromagnética . Alguns sustentavam que freqüências de luz e outros de radiação eletromagnética são compostos de partículas, enquanto outros afirmaram que a radiação eletromagnética é um fenômeno de onda. Na física clássica essas idéias são mutuamente contraditórias. Desde os primeiros dias de cientistas QM reconheceram que nem idéia por si só pode explicar a radiação eletromagnética.
Em 1690, Christian Huygens explicou as leis da reflexão e refração, com base em uma teoria de onda. Sir Isaac Newton acreditava que a luz consistia de partículas infinitamente pequenas que ele designadas "corpúsculos". Em 1827 Thomas Young e Augustin Fresnel feita em experiências interferências que mostrou que um teoria corpuscular da luz era inadequada. Em seguida, em 1873 James Clerk Maxwell mostraram que, ao fazer oscilar um circuito eléctrico, deve ser possível para a produção de ondas electromagnéticas. A sua teoria , foi possível calcular a velocidade de radiação electromagnética puramente na base de medições eléctricas e magnéticas, e o valor calculado correspondia muito de perto para o empiricamente medido velocidade da luz . Em 1888, Heinrich Hertz fez um dispositivo elétrico que realmente produziu o que hoje chamaríamos de microondas - essencialmente radiação a uma menor frequência do que a luz visível. Tudo até que ponto sugeriu que Newton tinha sido totalmente errado considerar a luz como corpuscular.
Experimentos posteriores indicaram que era necessário um modelo de pacote ou quântica para explicar alguns fenômenos. Quando a luz atinge um condutor elétrico faz com que os elétrons se afastar de suas posições originais. O fenómeno observado apenas pode ser explicado assumindo que a luz fornece energia em pacotes definidos. Em um dispositivo fotoelétrico, como o medidor de luz em uma câmera, a luz que atinge o detector de metal faz com que os elétrons se movam. Maior intensidades de luz em um freqüência pode causar mais elétrons se mover, mas eles não vão se mover mais rápido. Em contraste, a maior freqüências de luz podem causar elétrons se mover mais rápido. Ergo, a intensidade de controles de luz atual, mas a freqüência de controles de luz Tensão. Estas observações levantaram uma contradição, quando comparado com as ondas sonoras e ondas do mar, onde foi apenas necessário intensidade para prever a energia da onda. No caso da luz, a frequência apareceu para prever a energia. Foi necessário algo para explicar este fenómeno e para conciliar experimentos que mostraram ter luz partícula natureza com experimentos que mostraram que ele tem onda natureza.
Apesar do sucesso da mecânica quântica, ele tem alguns elementos controversos. Por exemplo, o comportamento de objetos microscópicos descritos na mecânica quântica é muito diferente da nossa experiência cotidiana, o que pode provocar um certo grau de incredulidade. A maior parte da física clássica é agora reconhecida a ser composta de casos especiais de teoria física quântica e / ou teoria da relatividade. Dirac trouxe a teoria da relatividade para suportar sobre física quântica para que pudesse lidar adequadamente com os eventos que ocorrem em uma fração substancial da velocidade da luz. A física clássica, no entanto, também lida com a atração de massa (gravidade), e ninguém ainda foi capaz de trazer a gravidade em uma teoria unificada com a teoria quântica relativizados.
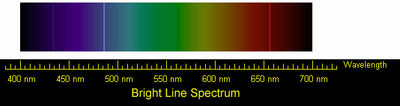
Espectroscopia e para a frente
É bastante fácil ver um espectro produzido por uma luz branca quando ele passa através de um prisma, a borda chanfrada de um espelho ou um painel cônico de vidro, ou por meio de gotas de chuva para formar um arco-íris. Quando as amostras que são compostos exclusivamente de um único elemento químico de hidrogênio por exemplo, são obrigados a emitir luz que pode emitir luz em várias frequências características. O perfil de frequência produzida é característica desse elemento. Em vez de existir uma banda de largura preenchido com cores de violeta para vermelho, haverá bandas isoladas de cores individuais separados por escuridão. Essa exibição é chamado de espectro de linha. Algumas linhas de ir além das frequências visíveis e só pode ser detectada por um filme fotográfico especial ou outros dispositivos. Os cientistas a hipótese de que um átomo poderia irradiar a luz na direção da corda em uma multa violino irradia som - não só com uma frequência fundamental (em que toda a cadeia se move da mesma maneira ao mesmo tempo), mas com vários harmónicos superiores (formada quando a corda se divide em metades e outras divisões que vibram em coordenação com os outros como quando uma metade do seqüência de caracteres é indo em uma direção como a outra metade da corda está indo na direção oposta). Por um longo tempo ninguém poderia encontrar uma maneira matemático que relacionasse as freqüências do espectro linha de qualquer elemento.
Em 1885, Johann Jakob Balmer (1825-1898) descobriu como as frequências de hidrogênio atômico estão relacionados uns aos outros. A fórmula é simples:
onde  comprimento de onda é, R é a Rydberg constante e n é um número inteiro (n = 3, 4, ...) Esta fórmula pode ser generalizada para aplicar a átomos que são mais complicados do que hidrogénio, mas que vai ficar com hidrogénio durante esta exposição geral. (Isto é a razão que o denominador na primeira fracção é expressa como um quadrado).
comprimento de onda é, R é a Rydberg constante e n é um número inteiro (n = 3, 4, ...) Esta fórmula pode ser generalizada para aplicar a átomos que são mais complicados do que hidrogénio, mas que vai ficar com hidrogénio durante esta exposição geral. (Isto é a razão que o denominador na primeira fracção é expressa como um quadrado).
O desenvolvimento seguinte foi a descoberta do Efeito Zeeman, em homenagem a Pieter Zeeman (1865-1943). A explicação física do efeito Zeeman foi elaborado por Hendrik Antoon Lorentz (1853-1928). Lorentz a hipótese de que a luz emitida por hidrogénio foi produzido por electrões de vibração. Foi possível obter feedback sobre o que se passa dentro do átomo porque os elétrons em movimento criam um campo magnético e assim pode ser influenciada pela imposição de um campo magnético externo de um modo análogo à maneira que um ímã de ferro vai atrair ou repelir um outro ímã .
O efeito Zeeman poderia ser interpretado no sentido de que as ondas de luz são originados por elétrons vibrando em suas órbitas, mas a física clássica não poderia explicar por que elétrons não deve cair fora de suas órbitas e no núcleo de seus átomos, nem poderia física clássica explicar por que a sua órbitas seria de modo a produzir a série de frequências discretas derivadas pela fórmula de Balmer e apresentados nos espectros de linha. Por que os elétrons não produzir um espectro contínuo?
Velha teoria quântica
A mecânica quântica desenvolvidas a partir do estudo de ondas eletromagnéticas através de espectroscopia , que inclui a luz visível visto nas cores do arco-íris, mas também outras ondas incluindo as ondas mais enérgicas, como luz ultravioleta, raios-x e raios gama e as ondas com comprimentos de onda mais longos, incluindo infravermelho ondas, micro-ondas e ondas de rádio. Só ondas que viajam à velocidade da luz estão incluídos nesta descrição. Além disso, quando a palavra "partícula" é utilizado abaixo, ele sempre se refere a partículas elementares ou subatômicas.
Constante de Planck
A física clássica previu que uma radiador de corpo negro iria produzir energia infinita, mas este resultado não foi observado no laboratório. Se a radiação de corpo negro foi disperso em um espectro, então a quantidade de energia irradiada a diferentes frequências aumentou de zero, numa extremidade, um pico com uma frequência relacionada com a temperatura do objecto radiante, e em seguida caiu para zero. Em 1900, Max Planck desenvolveu uma equação empírica que poderia explicar as curvas de energia observados, mas não conseguiu harmonizá-la com a teoria clássica. Ele concluiu que as leis clássicas da física não se aplicam na escala atômica, como já havia sido assumido.
Neste relato teórico, Planck permitiu que todas as freqüências possíveis, todos os comprimentos de onda possíveis. No entanto, ele restringe a energia que é entregue. "Em física clássica, ... a energia de um determinado oscilador depende apenas da sua amplitude, e esta amplitude é sujeita a nenhuma restrição." Mas, de acordo com a teoria de Planck, a energia emitida por um oscilador é estritamente proporcional à sua frequência. Quanto mais elevada for a frequência, maior é a energia. Para chegar a essa conclusão teórica, ele postulou que um corpo irradiando consistiu de um enorme número de osciladores elementares, alguns vibrando em uma freqüência e alguns em outro, com todas as freqüências de zero ao infinito a ser representado. A energia E de qualquer um oscilador não foi autorizado a assumir qualquer valor arbitrário, mas foi proporcional à algum múltiplo integral da f do oscilador de frequência. Isto é,
onde n = 1, 2, 3, ... A constante de proporcionalidade h é chamada Constante de Planck.
Uma das aplicações mais diretas é encontrar a energia de fótons . Se H é conhecida, e a frequência do fotão é conhecida, então a energia dos fotões pode ser calculada. Por exemplo, se um feixe de luz iluminada um alvo, e a sua frequência era de 540 × 10 12 Hertz, em seguida, a energia de cada fotão seria h 540 × 10 × 12 joules. O valor de h em si é muito pequena, cerca de 6.6260693 × 10 -34 segundo joule. Isto significa que os fotões no feixe de luz tem uma energia de cerca de 3,58 x 10 -19 joules ou (num outro sistema de medição) de aproximadamente 2,23 eV.
Quando a energia de uma onda é descrito desta forma, parece que a onda está a levar a sua energia em pequenos pacotes. Esta descoberta depois pareceu refazer a onda em uma partícula. Estes pacotes de energia realizadas junto com a onda foram chamados quanta por Planck. A mecânica quântica iniciou-se com a descoberta de que a energia é entregue em pacotes, cujo tamanho está relacionado com as frequências de todas as ondas electromagnéticas (e para a cor de luz visível, uma vez que em caso de frequências determina a cor). Esteja ciente, no entanto, que essas descrições em termos de pacotes, onda e partícula de importação conceitos macro-mundo para o mundo quântico, onde eles têm apenas relevância provisória ou adequação.
Em primeiras pesquisas sobre luz, havia duas maneiras concorrentes para descrever luz, seja como uma onda propagada através do espaço vazio, ou partículas tão pequenas que viajam em linhas retas. Porque Planck mostrou que a energia da onda é composto por pacotes, a analogia de partículas tornou-se favorecido para ajudar a compreender como a luz fornece energia em múltiplos de determinados valores definidos designados como quanta de energia. No entanto, a analogia onda também é indispensável para ajudar a compreender outros fenómenos de luz. Em 1905, Albert Einstein usou a constante de Planck para explicar o efeito fotoelétrico, postulando que a energia em um feixe de luz ocorre em concentrações que ele chamou de quanta de luz, mais tarde chamados de fótons . De acordo com essa conta, um único fóton de uma dada frequência administra uma quantidade invariante de energia. Em outras palavras, pode proporcionar fotões individuais mais ou menos energia, mas apenas de acordo com as suas frequências. Embora a descrição que resultou da pesquisa de Planck soa como conta corpuscular de Newton, fóton de Einstein ainda foi dito ter uma frequência, ea energia do fóton foi contabilizada proporcional à freqüência. A conta de partícula tinha sido comprometida mais uma vez.
Tanto a idéia de uma onda ea idéia de uma partícula são modelos derivados da nossa experiência cotidiana. Nós não podemos ver fótons individuais. Nós só podemos investigar suas propriedades de forma indireta. Nós olhamos para alguns fenômenos, como o arco-íris de cores que vemos quando uma fina película de óleo repousa sobre a superfície de uma poça de água, e podemos explicar esse fenômeno para nós mesmos através da comparação com as ondas de luz. Nós olhamos para outros fenômenos, como a forma como um medidor fotoelétrico em nossa câmera funciona, e nós explicar por analogia às partículas colidem com a tela de detecção no medidor. Em ambos os casos nós levamos conceitos da nossa experiência cotidiana e aplicá-los a um mundo que nunca vimos.
Nem a forma de explicação, onda ou partícula, é inteiramente satisfatória. Em geral, qualquer modelo só pode aproximar aquilo que modelos. Um modelo é útil apenas dentro do intervalo das condições em que é capaz de prever a coisa real com precisão. física newtoniana ainda é um bom preditor de muitos dos fenômenos em nossa vida cotidiana. Para lembrar-nos que tanto a "onda" e "partícula" são conceitos importados de nosso mundo macro para explicar o mundo dos fenômenos em escala atômica, alguns físicos, tais como George Gamow ter usado o termo " wavicle "para referir-se o que é que está realmente lá. Na discussão a seguir, "vaga" e "partícula" pode tanto ser usado dependendo de qual aspecto do fenômeno da mecânica quântica está em discussão.
Reduzida (ou de Dirac) constante de Planck

Constante de Planck representado inicialmente a energia que carrega uma onda de luz como uma função da sua frequência. Um passo no desenvolvimento deste conceito apareceu no trabalho de Bohr. Bohr estava usando um modelo de partículas ou "planetário" do elétron, e não conseguia entender por que um fator 2π foi essencial para suas fórmulas experimentalmente derivados. Mais tarde, de Broglie postulou que os elétrons têm freqüências, assim como fazer fótons, e que a frequência de um elétron deve estar de acordo com as condições para uma onda estacionária que pode existir num determinado órbita. Ou seja, o início de um ciclo de uma onda em algum ponto na circunferência de um círculo (que é o que é uma órbita) deve coincidir com o fim de algum ciclo. Não pode haver nenhuma lacuna, nenhum comprimento ao longo da circunferência que não está participando da vibração, e não pode haver sobreposição de ciclos. Assim, a circunferência da órbita, C, deve ser igual ao comprimento de onda, λ, do electrão multiplicado por algum número inteiro positivo (n = 1, 2, 3 ...). Sabendo a circunferência pode-se calcular que comprimentos de onda que se encaixam órbita, e conhecendo o raio, R, da órbita pode-se calcular a sua circunferência. Para colocar tudo isso em forma matemática,
então
e o aparecimento do factor de 2π é visto a ocorrer simplesmente porque é necessário para calcular possíveis comprimentos de onda (e, portanto, possíveis frequências) quando o raio de uma órbita já é conhecida.
Novamente em 1925, quando Werner Heisenberg desenvolveu sua teoria quântica completa, os cálculos que envolvem a análise da onda chamada Séries de Fourier foram fundamentais, e assim a versão "reduzida" de constante de Planck (h / 2π) tornou-se inestimável porque inclui um fator de conversão para facilitar os cálculos que envolvem a análise das ondas. Finalmente, quando esta reduziu constante de Planck apareceu naturalmente na equação de Dirac foi então dado uma designação alternativa ", Dirac de constante." Portanto, é apropriado começar com uma explicação sobre o que este é constante, embora as teorias que fizeram o seu uso conveniente, mas tem que ser discutido.
Como mencionado acima, a energia de qualquer onda é dada por sua frequência multiplicado por constante de Planck. Uma onda é composta de cristas e vales. Em uma onda, um ciclo é definido pelo retorno de uma certa posição na mesma posição tal como a partir do topo de uma crista para a crista seguinte. Um ciclo realmente é matematicamente relacionado com um círculo, e ambos possuem 360 graus. Um grau é uma unidade de medida para a quantidade de vez necessária para produzir um arco de um certo comprimento a uma determinada distância. A curva sinusoidal é gerado por um ponto na circunferência de um círculo como que gira círculo. (Veja uma demonstração em: Rotação Applet) Existem 2π radianos por ciclo em uma onda, que é matematicamente relacionado com a forma de um círculo tem 360 ° (que são iguais a dois π radianos). (Um radiano é simplesmente o ângulo se uma distância ao longo da circunferência do círculo é medido igual ao raio do círculo, e em seguida, as linhas são desenhadas para o centro do círculo. Isto forma um ângulo igual a 1 radiano.) Uma vez que uma ciclo é 2π radianos, quando h é dividida por 2π os dois fatores "2 π" cancelará deixando apenas o radiano de enfrentar. Então, dividindo h por 2π descreve uma constante que, quando multiplicada pela frequência de uma onda, dá a energia em joules por radiano. A constante reduzida de Planck é escrito em fórmulas matemáticas como H, e é lido como "h-bar".
 .
.
A constante de Planck reduzida permite a computação da energia da onda em unidades por radiano em vez de em unidades por ciclo. Estas duas constantes h e H são apenas factores de conversão entre unidades de energia e unidades de freqüência. A reduzida a constante de Planck é usado mais frequentemente do que h (a constante de Planck) sozinho em fórmulas matemáticas da mecânica quântica, por muitas razões, uma das quais é que a velocidade angular ou frequência angular é normalmente medido em radianos por segundo assim que usar ħ que funciona em radianos também será salvar um cálculo para colocar radianos em graus ou vice-versa. Além disso, quando equações relevantes para esses problemas são escritos em termos de H, os que ocorrem com frequência fatores 2π em numerador eo denominador pode cancelar para fora, salvar um cálculo. No entanto, noutros casos, como nas órbitas do átomo de Bohr, h / 2π foi obtido naturalmente para a quantidade de movimento angular das órbitas. Outra expressão para a relação entre energia e comprimento de onda é dada em elétron-volts de energia e de angstroms de comprimento de onda: E fóton (eV) = 12.400 / λ (A) - não parece envolver h em tudo, mas isso é só porque um diferente sistema de unidades foi usado e agora, numericamente, o fator de conversão apropriado é 12.400.
Átomo de Bohr

Em 1897, a partícula chamada elétron foi descoberto. Por meio do os físicos experimentais folha de ouro descobriu que a matéria é, o volume para o volume, em grande parte do espaço. Uma vez que ficou claro, se a hipótese de que as entidades de carga negativa chamadas elétrons cercam carregados positivamente núcleos . Assim, à primeira todos os cientistas acreditavam que o átomo deve ser como um sistema solar em miniatura. Mas essa analogia simples previu que os elétrons seria, dentro de cerca de um centésimo de um microssegundo, impacto no núcleo do átomo. A grande questão do início do século 20 foi: "Por que os elétrons normalmente manter uma órbita estável ao redor do núcleo?"
Em 1913, Niels Bohr removido esse problema substancial, aplicando a idéia de quanta discreto (não contínuo) para as órbitas de elétrons. Essa conta ficou conhecido como o Modelo de Bohr do átomo. Bohr basicamente a teoria de que os elétrons só pode habitar certas órbitas em torno do átomo. Estas órbitas poderia ser derivado de olhar para as linhas espectrais produzidos por átomos.
Bohr explicadas as órbitas que os electrões podem tomar pela relação entre o momento angular de electrões em cada órbita "permitido" para o valor de h, a constante de Planck. Ele declarou que um elétron no orbital menor tem um momento angular discreta igual a h / 2π. Cada órbita após a órbita inicial deve prever o momento angular de um electrão de ser um número inteiro múltiplo do valor mais baixo que. Ele representado elétrons em átomos como sendo análogo ao planetas em órbita solar. No entanto, ele tomou a constante de Planck para ser uma quantidade fundamental que introduz exigências especiais a este nível subatômico e que explica o espaçamento destas órbitas "planetárias".
Bohr considerada uma revolução em órbita a ser equivalente a um ciclo em um oscilador (como em medições iniciais de Planck para definir a constante h), que por sua vez é semelhante a um ciclo de uma onda. O número de rotações por segundo é (ou define) que nós chamamos a freqüência do elétron ou que orbital. Especificando que a frequência de cada órbita deve ser um múltiplo inteiro da constante de Planck h só permitir certas órbitas, e também fixar o seu tamanho.
Bohr generalizada A fórmula de Balmer para o hidrogênio, substituindo o termo denominador em 1/4 com uma variável quadrado explícito:
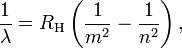 m = 1,2,3,4,5, ..., e n> m
m = 1,2,3,4,5, ..., e n> m
onde λ é o comprimento de onda da luz, R H é a Constante de Rydberg para o hidrogênio, e os inteiros N e M consulte as órbitas entre os quais os elétrons podem trânsito. Esta generalização previu muitos mais espectros de linha do que já havia sido detectado, e confirmação experimental desta previsão seguido.
Daqui resulta que se quase imediatamente  é quantificado como a fórmula acima indica, então o momento de qualquer de fotões devem ser quantizado. A frequência da luz,
é quantificado como a fórmula acima indica, então o momento de qualquer de fotões devem ser quantizado. A frequência da luz,  , A um dado comprimento de onda
, A um dado comprimento de onda  é dado pela relação
é dado pela relação
 e:
e:  e multiplicando por h / h = 1,
e multiplicando por h / h = 1,
 , E sabemos que
, E sabemos que
- E = hv assim
 que podemos reescrever como:
que podemos reescrever como:
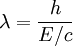 E E / C = P (impulso) de modo
E E / C = P (impulso) de modo
 ou
ou 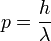
Começando com espectros de linha, os físicos foram capazes de deduzir, empiricamente as regras segundo as quais as órbitas de elétrons são determinados e para descobrir algo vital sobre os momentums envolvidos - que eles são quantificados.
Bohr próxima realizado como o momento angular de um electrão na sua órbita, G, é quantificado, ou seja, ele determinou que há algum valor constante K de tal modo que quando é multiplicado pela constante de Planck, h, que irá produzir o momento angular que pertence para o menor orbital. Quando é multiplicado por inteiros sucessivas que dará então os valores possíveis de outros orbitais. Mais tarde, ele determinou que K = 1 / 2π. (Veja o argumento detalhado em .)
A teoria de Bohr representada como elétrons orbitando o núcleo de um átomo de uma forma que foi surpreendentemente diferente do que vemos no mundo da nossa experiência cotidiana. Ele mostrou que, quando um elétron mudou órbitas não se mexeu em uma trajetória contínua de uma órbita ao redor do núcleo para outro. Em vez disso, ele de repente desapareceu de sua órbita original e reapareceu em outra órbita. Cada distância à qual um electrão pode órbita é uma função de um valor quantizado de energia. O mais perto do núcleo um órbitas de elétrons, menos energia é preciso para permanecer nesse orbital. Elétrons que absorvem um fóton ganhar um quantum de energia, de modo que ir para uma órbita que é mais longe do núcleo, enquanto os elétrons que emitem um fóton perder um quantum de energia e assim por saltar para um orbital interior. Os elétrons não pode ganhar ou perder um quantum fracionária de energia, e por isso, argumenta-se, eles não podem ter uma posição que está a uma distância fraccionada entre orbitais permitidos. Orbitais de estimação foram designados como números inteiros, utilizando a letra N com a mais interna orbital sendo designado n = 1, o próximo a ser n = 2, e assim por diante. Qualquer orbital com o mesmo valor de n é chamado uma camada electrónica.
Modelo do átomo de Bohr era essencialmente bidimensional porque retrata elétrons como partículas em órbitas circulares. Neste contexto, bidimensional significa algo que pode ser descrito na superfície de um avião. Unidimensional significa algo que pode ser descrito por uma linha. Porque círculos pode ser descrito pelo seu raio, que é um segmento de recta, às vezes modelo do átomo de Bohr é descrito como unidimensional.
Dualidade onda-partícula

Niels Bohr determinou que é impossível descrever luz adequadamente pela utilização exclusiva de um ou outro a analogia onda ou partícula da analogia. Portanto, ele enunciou a princípio da complementaridade, que é uma teoria de pares, tais como o emparelhamento de onda e de partícula ou o emparelhamento de posição e força. Louis de Broglie trabalhou as consequências matemáticas destes resultados. Na mecânica quântica, verificou-se que as ondas eletromagnéticas poderiam reagir em determinadas experiências como se fossem partículas e em outras experiências, como se fossem ondas. Descobriu-se também que as partículas subatómicas, por vezes, pode ser descrito na forma de partículas e, por vezes, como ondas. Esta descoberta levou à teoria da dualidade onda-partícula por Louis-Victor de Broglie em 1924, que afirma que as entidades subatômicas têm propriedades de ambas as ondas e partículas, ao mesmo tempo.
O modelo de átomo de Bohr foi ampliado em cima com a descoberta por de Broglie que o elétron tem propriedades wave-like. De acordo com as conclusões de de Broglie, os elétrons só pode aparecer em condições que permitem uma onda estacionária. Uma onda de pé pode ser feito se uma string é fixado em ambas as extremidades e fez vibrar (como faria em um instrumento de cordas). Essa figura mostra que as únicas ondas estacionárias que podem ocorrer são aqueles com amplitude zero nas duas extremidades fixas. As ondas criadas por um instrumento de cordas parecem oscilar no lugar, simplesmente mudando crista para calha em um movimento para cima e para baixo. Uma onda de pé só pode ser formado quando o comprimento de onda se encaixa a entidade de vibração disponível. Em outras palavras, não há fragmentos parciais de cristas das ondas ou calhas são permitidos. Em um meio de vibração rodada, a onda deve ser uma formação contínua de cristas e vales ao redor do círculo. Cada elétron deve ser a sua própria onda estacionária em seu próprio discreto orbital.
Desenvolvimento da mecânica quântica moderna
Teoria da mecânica quântica completa
Werner Heisenberg fez a teoria da mecânica quântica completa em 1925 com a idade de 23. Depois de seu mentor, Niels Bohr, Werner Heisenberg começou a elaborar uma teoria para o comportamento quântico de orbitais de elétrons. Porque electrões não pode ser observado nas suas órbitas, Heisenberg foi sobre a criação de uma descrição matemática da mecânica quântica construído sobre o que pode ser observado, isto é, a luz emitida a partir de átomos nos seus espectros atómica característica. Heisenberg estudou o elétron orbital no modelo de uma bola carregada em uma mola, um oscilador, cujo movimento é anharmonic (não muito regular). Para uma imagem do comportamento de uma bola carregada em uma mola ver: Vibrando Encargos. Heisenberg primeiro explicou este tipo de movimento observado em termos das leis da mecânica clássica conhecida para aplicar no mundo macro, e em seguida aplicou restrições quântica, discretos propriedades (não contínuas), com a imagem. Isso faz com que as lacunas a aparecer entre os orbitais previstos para que a descrição matemática ele formulou, então, representam apenas o elétron orbitais previsto com base dos espectros atômica.
Ao abordar o problema que Bohr deu-lhe para resolver, Heisenberg tomou a posição estratégica que ele não iria lidar com quantidades não observáveis. Ele iria começar a formular equações usando apenas as quantidades que podem ser observados. Essa estratégia levou a começar com a evidência experimental real na mão: Medidas tinha sido bem estabelecido para esses dados como: (1) as freqüências (e as energias matematicamente relacionados) emitida ou absorvida por transições de elétrons de uma das órbitas fixas Bohr, conhecido para ser associado com os espectros de linha brilhante, (2) a "amplitude transição" ou a probabilidade de transição de uma dada órbita para qualquer dada órbita, conhecido a partir da força das várias linhas no espectro luminoso, etc. De fórmulas clássicas que seria caracterizar esses fenômenos Heisenberg criado fórmulas análogas, que teve em conta as condições quântica. Fórmulas que se seguiram a partir das decisões fundamentais feitas neste momento resultou em bons resultados, mas resultados que às vezes não é o que se poderia esperar eram. No documento em que ele introduziu a mecânica quântica para o mundo ele adverte: "Uma dificuldade significativa surge, no entanto, se considerarmos duas quantidades x (t), y (t), e perguntar depois de seu produto .... Considerando que, na clássica x (t) y (t) é sempre igual a y (t) x (t), este não é necessariamente o caso em teoria quântica ". Quando os valores previstos são exibidos em forma de matriz e multiplicações são realizadas, a natureza da dificuldade aparece em uma forma que é mais familiar para os matemáticos.Mais significativamente, os estudos empíricos validar os resultados teóricos e sugerem que há algo de profunda importância em que a diferença entre x (t), y (t) e y (t) x (t) é um valor relacionado com a constante de Planck.
Esquema para uma tabela de freqüências de transição (produzido quando elétrons orbitais mudar):
| Electron Unidos | S1 | S2 | S3 | S4 | S5 | .... | |
|---|---|---|---|---|---|---|---|
| S1 | f1 1 → | F2 → 1 | F3 → 1 | f4 → 1 | f5 → 1 | ..... | |
| S2 | f1 2 → | 2 f2 → | f3 2 → | f4 → 2 | 2 F5 → | ..... | |
| S3 | f1 3 → | 3 F2 → | 3 F3 → | 3 f4 → | 3 F5 → | ..... | |
| S4 | f1 → 4 | F2 → 4 | F3 4 → | F4 4 → | f5 4 → | ..... | |
| S5 | f1 → 5 | F2 → 5 | F3 → 5 | f4 → 5 | f5 → 5 | ..... | |
| S ..... | ..... | ..... | ..... | ..... | ..... | ..... |
Esquema para uma tabela relacionada que mostra as amplitudes de transição:
| Electron Unidos | S1 | S2 | S3 | S4 | S5 | .... | |
|---|---|---|---|---|---|---|---|
| S1 | a1 1 → | a2 1 → | a3 1 → | a4 → 1 | A5 → 1 | ..... | |
| S2 | A1 → 2 | A2 2 → | A3 2 → | a4 2 → | A5 2 → | ..... | |
| S3 | A1 → 3 | a2 → 3 | A3 3 → | a4 3 → | A5 3 → | ..... | |
| S4 | A1 → 4 | a2 → 4 | A3 → 4 | A4 4 → | A5 4 → | ..... | |
| S5 | A1 → 5 | a2 → 5 | A3 → 5 | a4 → 5 | A5 5 → | ..... | |
| S ..... | ..... | ..... | ..... | ..... | ..... | ..... |
Como relatado acima, Heisenberg desenvolveram maneiras de significativamente relativa a informações em tabelas como estas de uma forma matemática. Empiricamente preenchendo os valores para os quadros que envolvem quantidades quânticas não é um procedimento simples, uma vez que qualquer medição feita em um único sistema que dá um valor, mas tem o potencial de alterar outros valores. Assim, um grande número de cópias idênticas do sistema em questão devem ser preparados, e uma única medida feita em cada sistema. Várias experiências para determinar as mesmas características são feitas, e os resultados são a média. Mesmo assim, as medições precisas de todas as características do sistema como eles aparecem ao mesmo tempo não pode ser fornecido por causa da incerteza quântica. A determinação precisa do valor de uma característica necessariamente cria uma incerteza no valor do seu correlato. "Certos pares de observáveis simplesmente não podem ser medidos simultaneamente para um nível elevado de precisão arbitrariamente. " Se as medições são feitas em simultâneo de características correlacionados (tais como a posição e quantidade de movimento) em vários sistemas idênticos, haverá inevitavelmente diferenças nas medidas de tal modo que a diferença entre os seus produtos é igual ou maior do que 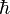 / 2 . "
/ 2 . "
Em 1925 Heisenberg publicou um artigo intitulado "re-interpretação da mecânica quântica das relações cinemáticas e mecânicas" relatando suas descobertas. Assim terminou a velha teoria quântica e começou a idade da mecânica quântica. Papel de Heisenberg deu alguns detalhes que podem ajudar os leitores na determinação de como ele realmente planejado para obter seus resultados para os modelos unidimensionais que ele usou para formar a hipótese de que se mostrou tão útil. Em seu artigo, Heisenberg propôs "descartar toda a esperança de observar quantidades até então não observáveis, como a posição eo período do elétron", e limitar-se estritamente às quantidades efectivamente observáveis. Ele precisava de regras matemáticas para prever as relações realmente observados na natureza, e as regras que ele produziu trabalhou de forma diferente dependendo da seqüência em que foram aplicadas. "Tornou-se rapidamente claro que a não-comutatividade (em geral) de quantidades cinemáticas em teoria quântica foi a idéia nova técnica realmente essencial no papel. "
O tipo especial de multiplicação que acabou por ser exigido em sua fórmula foi mais elegantemente descrito usando matrizes especiais de números chamados matrizes . Em situações normais, não importa em que ordem as operações envolvidas na multiplicação são realizados, mas a multiplicação de matrizes não comutar . Essencialmente, o que significa que é importante que as operações são executadas ordem dada na. Multiplicando matriz A matriz por B não é o mesmo que multiplicar matriz B por matriz A. Em símbolos, A X B é, em geral, não é igual a B × Uma. (O que é importante na teoria quântica é que ela acabou por importa se um experimentalmente mede a velocidade em primeiro lugar e, em seguida, imediatamente medidas de posição, ou vice-versa.) A convenção matriz acabou por ser uma forma conveniente de organizar a informação e deixando clara a exata sequência na qual deve ser feita cálculos, e que reflecte de forma simbólica os resultados inesperados obtidos no mundo real.
Heisenberg aproximou mecânica quântica a partir da perspectiva histórica que tratou um elétron como uma partícula oscilante cobrado. Uso de Bohr desta analogia já tinha lhe permitiu explicar por que os raios das órbitas dos elétrons só poderia assumir certos valores. Seguiu-se a partir desta interpretação dos resultados experimentais disponíveis e da teoria quântica que Heisenberg, posteriormente, criou um elétron que não poderia ser em qualquer posição intermediária entre dois "permitido" órbitas. Portanto elétrons foram descritos como "salto" de órbita em órbita. A idéia de que um elétron pode agora estar em um lugar e um instante depois estar em algum outro lugar sem ter viajado entre os dois pontos foi uma das primeiras indicações da "spookiness" dos fenômenos quânticos. Embora a escala é menor, a "saltar" de órbita em órbita é tão estranha e inesperada como seria um caso em que alguém saiu de uma porta em Londres para as ruas de Los Angeles. tunelamento quântico é um exemplo no qual os elétrons parecem para ser capaz de mover-se no caminho "assustador" que Heisenberg atribuída a suas ações dentro de átomos.
Amplitudes de posição e dinâmica que têm um período de 2 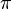 como um ciclo em uma onda são chamados de variáveis de série de Fourier. Heisenberg descreveu as propriedades da partícula semelhante a do elétron em uma onda como tendo a posição eo momento em sua mecânica matricial. Quando essas amplitudes de posição e momento são medidos e multiplicados juntos, eles dão intensidade. No entanto, ele descobriu que quando a posição eo momento foram multiplicados juntos nessa respectiva ordem e, em seguida, o momento ea posição foram multiplicados juntos nessa respectiva ordem, havia uma diferença ou desvio na intensidade entre eles de h / 2
como um ciclo em uma onda são chamados de variáveis de série de Fourier. Heisenberg descreveu as propriedades da partícula semelhante a do elétron em uma onda como tendo a posição eo momento em sua mecânica matricial. Quando essas amplitudes de posição e momento são medidos e multiplicados juntos, eles dão intensidade. No entanto, ele descobriu que quando a posição eo momento foram multiplicados juntos nessa respectiva ordem e, em seguida, o momento ea posição foram multiplicados juntos nessa respectiva ordem, havia uma diferença ou desvio na intensidade entre eles de h / 2 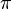 . Heisenberg não entenderia a razão para este desvio até mais dois anos se passaram, mas, por enquanto, ele satisfez-se com a ideia de que a matemática trabalhou e forneceu uma descrição exata do comportamento quântico do elétron.
. Heisenberg não entenderia a razão para este desvio até mais dois anos se passaram, mas, por enquanto, ele satisfez-se com a ideia de que a matemática trabalhou e forneceu uma descrição exata do comportamento quântico do elétron.
Mecânica matricial foi a primeira definição completa da mecânica quântica, as suas leis, e propriedades que descrevem completamente o comportamento do elétron. Posteriormente, foi alargado aos todas as partículas subatômicas. Logo depois mecânica matricial foi introduzido ao mundo, Schrödinger, agindo de forma independente, produziu uma teoria quântica de onda que parecia não ter semelhanças modo algum, em teoria de Heisenberg. Foi computacionalmente mais fácil e evitar algumas das idéias impar-soar como "saltos quânticos" de um elétron de uma órbita para outra. Mas dentro de um curto período de tempo se Schrödin tinham mostrado que as duas teorias produzido essencialmente os mesmos resultados em todas as situações. Finalmente, Dirac fez a idéia de não-comutatividade central para sua própria teoria e provou as formulações de Heisenberg e de Schrödinger para ser casos especiais de sua própria teoria.
Equação de onda de Schrödinger

Porque as partículas poderiam ser descritos como ondas, mais tarde, em 1925, Erwin Schrödinger analisado o que um elétron se pareceria como uma onda em torno do núcleo do átomo. Usando esse modelo, ele formulou sua equação para ondas de partículas. Em vez de explicar o átomo por analogia, aos satélites em órbitas planetárias, ele tratou tudo como ondas através do qual cada elétron tem a sua própria função de onda único. A função de onda é descrito na equação de Schrödinger por três propriedades (mais tarde Wolfgang Pauli acrescentou uma quarta). Os três propriedades foram (1) uma designação "orbital", que indica se a onda de partícula é aquele que está mais próximo do núcleo com menos energia ou um que é mais distante do núcleo com mais energia, (2) a forma da orbital, isto é, uma indicação de que orbitais não eram apenas formas esféricas, mas outros, e (3) o momento magnético da orbital, que é uma manifestação da força exercida pela carga do electrão à medida que roda em torno do núcleo.
Essas três propriedades foram chamados coletivamente a função de onda do elétron e são disse para descrever o estado quântico do elétron. "Estado quântico" significa que as propriedades coletivas do elétron descrevendo o que podemos dizer sobre a sua condição em um determinado momento. Para o elétron, o estado quântico é descrito por sua função de onda, que é designado em física pela letra grega 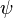 (psi, pronuncia-se "suspiro"). As três propriedades da equação de Schrödinger que descrevem a função de onda do elétron e, portanto, também descrevem o estado quântico do elétron como descrito no parágrafo anterior são cada chamados números quânticos. A primeira propriedade que descreve a orbital foi contado de acordo com o modelo de Bohr, onde n é a letra utilizado para descrever a energia de cada orbital. Isso é chamado de número quântico principal. O próximo número quântico que descreve a forma da orbital é chamado o número quântico azimutal e que é representada pela letra L (minúsculas L). A forma é causada pelo movimento angular do orbital. A taxa de variação do momento angular de qualquer sistema é igual ao binário externo resultante agindo nesse sistema. Em outras palavras, o momento angular representa a resistência de um objecto de fiação para acelerar ou desacelerar sob a influência da força externa. O número quântico azimutal "l" representa o momento angular orbital do elétron em torno de seu núcleo. No entanto, a forma de cada orbital tem a sua própria letra bem. Assim, para a letra "l" há outras letras para descrever as formas de "l" . A primeira forma é esférica e é descrito pela letra s . A forma seguinte é como um haltere e é descrito pela letra p . As outras formas de orbitais tornar-se mais complicado (ver orbitais atómicas) e são descritos pelas letras d , f , e g . Para a forma de um átomo de carbono, ver átomo de carbono. O terceiro número quântico da equação de Schrödinger descreve o momento magnético do elétron e é designada pela letra m e às vezes como a letra m com um subscrito l porque o momento magnético depende do segundo número quântico l .
(psi, pronuncia-se "suspiro"). As três propriedades da equação de Schrödinger que descrevem a função de onda do elétron e, portanto, também descrevem o estado quântico do elétron como descrito no parágrafo anterior são cada chamados números quânticos. A primeira propriedade que descreve a orbital foi contado de acordo com o modelo de Bohr, onde n é a letra utilizado para descrever a energia de cada orbital. Isso é chamado de número quântico principal. O próximo número quântico que descreve a forma da orbital é chamado o número quântico azimutal e que é representada pela letra L (minúsculas L). A forma é causada pelo movimento angular do orbital. A taxa de variação do momento angular de qualquer sistema é igual ao binário externo resultante agindo nesse sistema. Em outras palavras, o momento angular representa a resistência de um objecto de fiação para acelerar ou desacelerar sob a influência da força externa. O número quântico azimutal "l" representa o momento angular orbital do elétron em torno de seu núcleo. No entanto, a forma de cada orbital tem a sua própria letra bem. Assim, para a letra "l" há outras letras para descrever as formas de "l" . A primeira forma é esférica e é descrito pela letra s . A forma seguinte é como um haltere e é descrito pela letra p . As outras formas de orbitais tornar-se mais complicado (ver orbitais atómicas) e são descritos pelas letras d , f , e g . Para a forma de um átomo de carbono, ver átomo de carbono. O terceiro número quântico da equação de Schrödinger descreve o momento magnético do elétron e é designada pela letra m e às vezes como a letra m com um subscrito l porque o momento magnético depende do segundo número quântico l .
Em maio 1926 Schrödinger publicou uma prova de que a mecânica matricial de Heisenberg e suas próprias mecânica ondulatória deu resultados equivalentes matematicamente eles eram a mesma teoria. No entanto, os dois homens estavam em desacordo sobre a interpretação dessa teoria. Heisenberg não viu nenhum problema na existência de saltos quânticos descontínuas, enquanto Schrödinger esperava que uma teoria baseada em propriedades contínuas wave-like poderia evitar esse "nonsense sobre saltos quânticos" (nas palavras de Wilhelm Wien).
O princípio da incerteza
Em 1927, Heisenberg fez uma nova descoberta sobre a base de sua teoria quântica que teve consequências ainda mais práticos desta nova forma de olhar para a matéria ea energia em escala atômica. Em mecânica matricial de Heisenberg fórmula, ele encontrou um erro ou diferença de h / 2 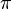 entre a posição eo momento. Quanto mais certeza de que a posição de uma partícula é determinado, a menos certo que o impulso é conhecido, e h / 2
entre a posição eo momento. Quanto mais certeza de que a posição de uma partícula é determinado, a menos certo que o impulso é conhecido, e h / 2 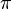 é o limite inferior da incerteza envolvida. Esta conclusão veio a ser chamado de "indeterminação de Heisenberg Principle", ou Princípio da Incerteza de Heisenberg.
é o limite inferior da incerteza envolvida. Esta conclusão veio a ser chamado de "indeterminação de Heisenberg Principle", ou Princípio da Incerteza de Heisenberg.
Para as partículas em movimento na mecânica quântica, não há simplesmente um certo grau de exatidão e precisão que está faltando. O observador pode ser preciso quando se toma uma posição de medição ou pode ser mais preciso, quando efectuar uma medição da quantidade de movimento, mas há uma imprecisão de medição inversa quando os dois ao mesmo tempo, como no caso de uma partícula em movimento, como o electrão. No caso mais extremo, a precisão absoluta de uma variável implicaria imprecisão absoluta em relação ao outro.
Heisenberg, em uma gravação de voz de uma palestra no início o princípio da incerteza apontando para um modelo de Bohr do átomo, disse:
- "Você pode dizer, bem, esta órbita não é realmente uma órbita completa. Na verdade, a cada momento o elétron tem apenas uma posição incorrecta e imprecisa e uma velocidade entre essas duas imprecisões existe essa relação de incerteza. E só por esta idéia que era possível para dizer o que tal órbita era. "
Uma conseqüência do princípio da incerteza foi que o elétron não poderia mais ser considerado como em um local exato em seu orbital. Pelo contrário, o elétron tinha de ser descrito por cada ponto onde o elétron poderia habitar. Calculando pontos de provável local para o elétron em sua conhecida orbital criado a imagem de uma nuvem de pontos em uma forma esférica para a orbital de um átomo de hidrogênio que aponta desvaneceu-se gradualmente para fora mais perto do núcleo e mais longe do núcleo. Esta imagem pode ser chamado de uma distribuição de probabilidade . Portanto, o número do átomo de Bohr n para cada orbital tornou-se conhecido como um n-esfera no átomo tridimensional e foi representada como uma nuvem, onde a probabilidade de electrões do átomo rodeado de uma só vez.
O termo eigenstate é derivado da palavra alemã / holandesa "eigen", que significa "inerente" ou "característica." A palavra eigenstate é descritiva do estado medido de algum objeto que possui características quantificáveis, tais como posição, força, etc. O estado que está sendo medido e descrito deve ser um " observável "(isto é algo que pode ser medido experimentalmente, directa ou indirectamente como posição ou momento), e deve ter um valor definido. No mundo todos os dias, é natural e intuitivo pensar em tudo estar em sua própria auto-estado. Tudo parece ter uma posição definida, um impulso definitivo, um valor definitivo da medida, e um tempo definido de ocorrência. No entanto, a mecânica quântica afirma que é impossível apontar valores exatos para a dinâmica de uma determinada partícula como um elétron em um determinado local em um determinado momento no tempo, ou, em alternativa, que é impossível dar um local exato para tal objeto quando o impulso foi medido. Devido ao princípio da incerteza, declarações relativas tanto a posição eo momento de partículas só pode ser dada em termos de uma série de probabilidades, uma "distribuição de probabilidade". Eliminando a incerteza em um prazo maximiza a incerteza em relação ao segundo parâmetro.
Por isso, tornou-se necessário ter uma maneira de formular claramente a diferença entre o estado de algo que é incerto na forma que acabamos de descrever, como um elétron em uma nuvem de probabilidade e, efetivamente, contrastá-la com o estado de algo que não é incerto, algo que tem um valor definitivo. Quando algo está na condição de ser definitivamente "pinado-down" em algum sentido, é dito possuir um auto-estado . Por exemplo, se a posição de um electrão foi feita definida, diz-se ter uma auto-estado de posição.
Um valor definido, tal como a posição de um electrão que foi localizada com êxito, é chamado o valor próprio do autoestado de posição. A palavra alemã "eigen" foi usado pela primeira vez neste contexto pelo matemático David Hilbert em 1904. equação de onda de Schrödinger dá soluções função de onda, ou seja, as possibilidades onde o elétron pode ser, assim como faz distribuição de probabilidade de Heisenberg. Tal como referido acima, quando um colapso da função de onda ocorre porque algo tem sido feito para localizar a posição de um electrão, o estado de electrões torna-se um auto-estado de posição, o que significa que a posição tem um valor conhecido.
O princípio de exclusão de Pauli
O Exclusão de Pauli Princípio afirma que nenhum elétron (ou outrofermion) pode estar no mesmo estado quântico como outro dentro de um átomo.
Wolfgang Pauli desenvolveu o Princípio de Exclusão do que ele chamou de um "grau quântico de dois valores de liberdade" para explicar a observação de um gibão, ou seja, um par de linhas, no espectro do átomo de hidrogênio. A observação significava que havia mais energia no elétron orbital do momento magnético do que tinha sido descrito anteriormente. No início de 1925, os jovens físicos Uhlenbeck e Goudsmit introduziu uma teoria de que o elétron gira no espaço da mesma forma que a Terra gira sobre seu eixo. Isso explicaria o momento magnético em falta e permitir dois elétrons no mesmo orbital para ser diferente se seus spins foram em direções opostas, satisfazendo, assim, o princípio de exclusão.
De acordo com a equação de Schrödinger, existem três estados quânticos do electrão, mas se dois electrões podem estar no mesmo orbital, tem de haver um outro número quântico (o grau quântico de dois valores de liberdade) para distinguir os dois electrões da outra . Um único elétron não pode ter os mesmos quatro números quânticos como outro elétron no mesmo orbital atômico. Onde dois elétrons estão no mesmo n-esfera e, portanto, compartilham o mesmo número quântico principal, eles devem então ter algum outro número quântico única de forma l , magnético momento m ou rotação s . Onde electrões não estão em um orbital em torno do núcleo de um átomo, tal como na formação de gases degenerados, que ainda tem de seguir o princípio de exclusão de Pauli quando em um espaço confinado.
Equação de onda de Dirac
Em 1928, Paul Dirac trabalhou fora uma variação da equação de Schrödinger, que representaram uma quarta propriedade do elétron em sua órbita. Paul Dirac introduzido o quarto número quântico chamado o número de spin quântico designada pela letra s para a nova equação de Dirac da função de onda do elétron. Em 1930, Dirac combinou a mecânica matricial de Heisenberg com mecânica ondulatória de Schrödinger em uma única representação mecânica quântica em seus princípios da mecânica quântica . A imagem de quantum do elétron foi agora concluída.
Todo o desenvolvimento acima da teoria quântica foi baseado principalmente no espectro atômico do átomo de hidrogênio. Isto é devido ao facto de que cada átomo de cada elemento produz um único padrão de linhas espectrais quando a luz a partir de cada tipo diferente de elemento é passado através de um prisma. Os cientistas não pudesse estudar o núcleo de electrões e do próprio átomo porque eles não podem ser vistos. Mesmo hoje, com de alta resolução Scanning Tunneling microscópios de electrões que só pode obter imagens do átomo como um fuzzball embaçada. No entanto, as linhas espectrais do átomo de revelar as órbitas dos electrões e a energia que pode ser esperada. Ele foi basicamente este estudo da análise espectroscópica do primeiro átomo de hidrogênio e, em seguida, o átomo de hélio que levou à teoria quântica. Portanto, as fórmulas matemáticas foram feitas para ajustar a imagem do espectro atômico. É por isso que a mecânica quântica é por vezes referido como uma forma de física matemática.
Emaranhamento quântico
Albert Einstein rejeitou Princípio da Incerteza de Heisenberg na medida em que parecia implicar mais do que é necessária uma limitação na capacidade humana para realmente saber o que ocorre no mundo quântico. Em uma carta a Max Born, em 1926, Einstein declarou famosa que "Deus não joga dados". A prescrição nível superfície nua para fazer previsões da mecânica quântica, com base na regra de Born para calcular probabilidades, ficou conhecido como a interpretação de Copenhague da mecânica quântica. Bohr passou muitos anos a desenvolver ea aperfeiçoar essa interpretação à luz das objeções de Einstein. Depois de 1930 Conferência Solvay, Einstein nunca mais desafiados a interpretação de Copenhaga sobre as questões técnicas, mas não cessou um ataque filosófico sobre a interpretação, por razões de realismo e localidade. Einstein, na tentativa de mostrar que a teoria quântica não era uma teoria completa, reconheceu que a teoria previa que duas ou mais partículas que interagiram no passado podem apresentar fortes correlações quando várias medições são feitas sobre eles. Ele queria que isso seja explicado de forma clássica através de seu passado comum, e de preferência não por um "assustador ação à distância ". O argumento é trabalhada em um famoso artigo dedicado ao que hoje é chamado o paradoxo EPR (Einstein-Podolsky-Rosen, 1935). Partindo do princípio de que é agora geralmente chamado de " realismo local ", o EPR tenta mostrar da teoria quântica que as partículas simultaneamente possuem tanto a posição eo momento, enquanto de acordo com a interpretação de Copenhaga, apenas uma dessas duas propriedades existe apenas brevemente, no momento em que ele está a ser medido. Einstein considerou que esta conclusão uma prova de que a teoria quântica era incompleta, uma vez que se recusa a discutir as propriedades físicas que objetivamente existem na natureza. O recurso da teoria quântica levando a esses paradoxos é chamado entrelaçamento quântico. Isso significa que as propriedades de vários objectos separados não pode ser descrito por considerá-los separadamente, mesmo tendo em conta a história do passado da sua interacção. O papel 1935 de Einstein, Podolsky e Rosen é atualmente publicação mais citadas de Einstein em revistas de física.
Resposta original de Bohr de Einstein era que as partículas eram parte de um sistema indivisível. O desafio de Einstein levou a décadas de pesquisa substancial em entrelaçamento quântico. A pesquisa parece confirmar a objeção de Bohr que as duas partículas entrelaçadas deve ser vista em conjunto como um todo, e, além disso, que as dificuldades só surgem ao insistir sobre a realidade dos resultados das medições que não são feitos de qualquer maneira. Além disso, Deus faz jogar dados, embora os bastante peculiares. Um lance de dados real pode ser completamente entendido com a mecânica clássica, eo resultado é uma mera função das condições iniciais. No entanto, o resultado de lançar dados quânticos não tem antecedente; nenhuma causa ou explicação.
Interpretações
De acordo com princípio da correspondência e teorema de Ehrenfest como um sistema torna-se maior ou mais massivo ( ação >> h ) a dinâmica clássica tende a emergir, com algumas exceções, como superfluidez. É por isso que normalmente pode ignorar a mecânica quântica quando se lida com objetos do cotidiano; em vez da descrição clássica será suficiente. Mesmo assim, tentando fazer o sentido da teoria quântica é um processo contínuo que tem gerado uma série de interpretações da teoria quântica, que vão desde o convencional interpretação de Copenhaga de variáveis ocultas e muitos mundos. Não parece não ter fim à vista para as reflexões filosóficas sobre o assunto; no entanto, o sucesso empírico ou técnico da teoria é inigualável; todas as teorias fundamentais da física moderna são teorias quântica, relatividade tifipicar teorias quânticas de campo.