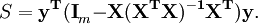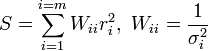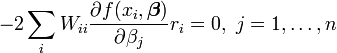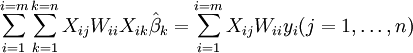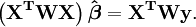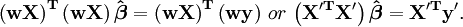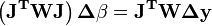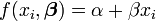Mínimos quadrados
Fundo para as escolas Wikipédia
Crianças SOS tentou tornar o conteúdo mais acessível Wikipedia por esta selecção escolas. Veja http://www.soschildren.org/sponsor-a-child para saber mais sobre apadrinhamento de crianças.
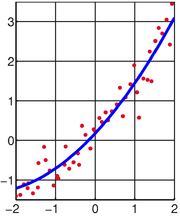
O método dos mínimos quadrados, também conhecido como análise de regressão , é usado para modelar os dados numéricos obtidos a partir de observações por ajuste dos parâmetros de um modelo de modo a obter um encaixe perfeito dos dados. O melhor ajuste é caracterizado por a soma dos residuais quadrados tem o seu valor mínimo, uma sendo residual a diferença entre um valor observado e o valor fornecido pelo modelo. O método foi descrito pela primeira vez por Carl Friedrich Gauss em torno de 1794. mínimos quadrados corresponde ao critério da máxima verossimilhança, se os erros experimentais têm uma distribuição normal . A análise de regressão está disponível na maioria pacotes de software estatísticos.
História
Contexto
O método dos mínimos quadrados cresceu a partir dos campos da astronomia e geodesia como cientistas e matemáticos procurou oferecer soluções para os desafios de navegar os oceanos da Terra durante a Era dos Descobrimentos . A descrição precisa do comportamento dos corpos celestes era essencial para permitir que navios a navegar em mar aberto onde antes marinheiros tiveram que contar com avistamentos de terra para determinar as posições de seus navios.
O método foi o culminar de vários avanços que ocorreram durante o curso do século XVIII :
- A combinação de diferentes observações feitas sob as mesmas condições ao invés de simplesmente tentar um melhor de observar e registar uma única observação com precisão. Esta abordagem foi notavelmente usado por Tobias Mayer, enquanto estudava o librations da lua.
- A combinação de observações diferentes como sendo a melhor estimativa do valor verdadeiro; erros diminuir com agregação em vez de aumento, talvez primeira expressa por Roger Cotes.
- A combinação de diferentes observações feitas em diferentes condições, como nomeadamente realizada por Roger Joseph Boscovich em seu trabalho sobre a forma da Terra e Pierre-Simon Laplace em seu trabalho para explicar as diferenças no movimento de Júpiter e Saturno .
- O desenvolvimento de um critério que pode ser avaliado para determinar quando a solução com o mínimo de erro tenha sido alcançado, desenvolvido por Laplace no seu Método de situação.
O método próprio
Carl Friedrich Gauss é creditado com o desenvolvimento dos fundamentos da base para a análise de mínimos quadrados em 1795 com a idade de dezoito anos.
Uma manifestação precoce da força do método de Gauss veio quando ele foi utilizado para prever o local do recém descoberto asteróide futuro Ceres . Em 1º de janeiro de 1801 , o astrônomo italiano Giuseppe Piazzi descobriu Ceres e foi capaz de acompanhar o seu caminho por 40 dias antes de ter sido perdido no brilho do sol. Com base nestes dados, foi desejado para determinar a localização de Ceres depois que surgiu de trás do sol, sem resolver o complicado equações não-lineares de Kepler do movimento planetário. As únicas previsões que permitiu com sucesso astrônomo húngaro Franz Xaver von Zach para mudar Ceres eram aqueles realizados pelo 24-year-old Gauss usando análise de mínimos quadrados.
Gauss não publicar o método até 1809 , quando apareceu em dois volumes de seu trabalho em mecânica celeste, Theoria Motus Corporum Coelestium em sectionibus conicis solem ambientium. Em 1829 , Gauss era capaz de afirmar que a abordagem de mínimos quadrados para análise de regressão é o ideal no sentido de que em um modelo linear em que os erros têm uma média de zero, não estão correlacionados, e têm variâncias iguais, os melhores estimadores imparciais lineares de os coeficientes são os estimadores de mínimos quadrados. Este resultado é conhecido como o Gauss-Markov teorema.
A idéia de mínimos quadrados análise também foi formulado de forma independente pelo francês Adrien-Marie Legendre em 1805 e da American Robert Adrain em 1808 .
Declaração do problema
O objectivo consiste em ajustar os parâmetros de uma função de modelo, de modo a melhor atender um conjunto de dados. Um conjunto de dados simples consiste em m pontos (pares de dados)  , I = 1, ..., m, onde
, I = 1, ..., m, onde 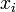 é um variável independente e
é um variável independente e  é um variável dependente cujo valor é encontrado por observação. A função de modelo tem a forma
é um variável dependente cujo valor é encontrado por observação. A função de modelo tem a forma 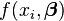 , Onde os parâmetros ajustáveis n são realizadas no vector
, Onde os parâmetros ajustáveis n são realizadas no vector  . Queremos encontrar os valores de parâmetros para que o modelo de "melhor" se ajusta aos dados. O método dos mínimos quadrados define "melhor" como quando a soma, S, de resíduos quadrados
. Queremos encontrar os valores de parâmetros para que o modelo de "melhor" se ajusta aos dados. O método dos mínimos quadrados define "melhor" como quando a soma, S, de resíduos quadrados
é um mínimo. A residual é definido como a diferença entre os valores da variável dependente e o modelo.
Um exemplo de um modelo que é da linha recta. Denotando a interceptação como  ea inclinação como
ea inclinação como 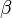 , A função modelo é dada pela
, A função modelo é dada pela
Ver linear de mínimos quadrados # Exemplo para um exemplo totalmente trabalhadas fora deste modelo.
Um ponto de dados pode consistir de mais do que uma variável independente. Por exemplo, aquando da montagem de um plano de um conjunto de medições da altura, o plano é uma função de duas variáveis independentes, X e Z, por exemplo. No caso mais geral, pode haver uma ou mais variáveis independentes e uma ou mais variáveis dependentes em cada ponto de dados.
A resolução do problema dos mínimos quadrados
Menos problemas quadrados se dividem em duas categorias, linear e não-linear. O problema lineares dos mínimos quadrados tem uma solução de forma fechada, mas o problema não linear tem de ser resolvido por refinamento iterativo; em cada iteração do sistema é aproximada por um processo linear, de modo que o cálculo do núcleo é semelhante em ambos os casos.
O mínimo da soma dos quadrados é encontrado, definindo a gradiente a zero. Uma vez que o modelo contém parâmetros n existem n equações gradiente.
e desde  as equações gradiente tornar
as equações gradiente tornar
As equações de gradiente aplicável a todos os problemas de mínimos quadrados. Cada problema particular requer expressões particulares para o modelo e suas derivadas parciais.
Linear de mínimos quadrados
O sistema é um processo linear, quando o modelo compreende um combinação linear dos parâmetros.
Os coeficientes 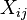 são constantes ou funções da variável independente, x i.
são constantes ou funções da variável independente, x i.
Desde 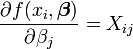 e
e 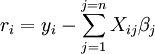 as equações gradiente tornar
as equações gradiente tornar
que, por rearranjo, tornar-se equações lineares n simultâneas, as equações normais.
As equações normais são escritos em notação matricial como
Solução das equações normais produz os estimadores de mínimos quadrados,  , Dos valores dos parâmetros. Ver lineares de mínimos quadrados (exemplo) e regressão linear (exemplo) para exemplos numéricos trabalhou-out.
, Dos valores dos parâmetros. Ver lineares de mínimos quadrados (exemplo) e regressão linear (exemplo) para exemplos numéricos trabalhou-out.
Mínimos quadrados não-lineares
Não há uma solução fechada para um problema menos não linear quadrados. Em vez disso, os valores iniciais deve ser escolhido para os parâmetros. Em seguida, os parâmetros são iterativamente refinado, isto é, os valores são obtidos por aproximação sucessiva.
k é um número de iteração e o vector de incrementos, 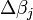 é conhecido como o vector de deslocamento. Em cada iteração O modelo pode ser linearizado por aproximação de primeira ordem da série de Taylor de expansão sobre
é conhecido como o vector de deslocamento. Em cada iteração O modelo pode ser linearizado por aproximação de primeira ordem da série de Taylor de expansão sobre 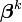
O Jacobiana, J, é uma função de constantes, a variável independente e os parâmetros, de modo que muda de uma iteração para a próxima. Os resíduos são dadas pela
e as equações de gradiente tornar
que, por rearranjo, tornar-se equações lineares n simultâneas, as equações normais.
As equações normais são escritos em notação matricial como
Estas são as equações que definem a Algoritmo de Gauss-Newton.
As diferenças entre linear e mínimos quadrados não-lineares
- A função de modelo, f, em LLSQ (linear dos mínimos quadrados) é uma combinação linear dos parâmetros da forma de
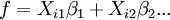 O modelo pode representar uma linha reta, uma parábola ou qualquer outra função do tipo polinomial. Em NLLSQ (não-lineares de mínimos quadrados) os parâmetros aparecem como funções, tais como
O modelo pode representar uma linha reta, uma parábola ou qualquer outra função do tipo polinomial. Em NLLSQ (não-lineares de mínimos quadrados) os parâmetros aparecem como funções, tais como 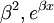 e assim por diante. Se os derivados
e assim por diante. Se os derivados 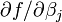 são constantes ou apenas dependentes dos valores da variável independente, o modelo é linear nos parâmetros. Caso contrário, o modelo é não linear.
são constantes ou apenas dependentes dos valores da variável independente, o modelo é linear nos parâmetros. Caso contrário, o modelo é não linear. - NLLSQ requer valores iniciais para os parâmetros, LLSQ não.
- NLLSQ requer que o Jacobiana ser calculada. Expressões analíticas para as derivadas parciais podem ser complicados. Se expressões analíticas são impossíveis de obter as derivadas parciais deve ser calculado por aproximação numérica.
- Em NLLSQ divergência é um fenómeno comum ao passo que em LLSQ é muito raro. A divergência ocorre quando a soma dos quadrados aumenta de uma iteração para a próxima. É causada pela inadequação da aproximação que a série Taylor pode ser truncado no primeiro mandato. Quando ocorre divergência do método devem ser modificados. O Algoritmo Levenberg-Marquardt fornece boa proteção contra a divergência girando o vetor deslocamento para a direção da descida mais íngreme. Pela convergência definição é assegurada quando os pontos de mudança de vetor no sentido da descida mais íngreme.
- NLLSQ é um processo iterativo process.The inerentemente iterativa tem de ser encerrado quando um critério de convergência está satisfeito. LLSQ soluções pode ser calculada usando métodos directos, apesar de problemas com um grande número de parâmetros são tipicamente resolvidos através de métodos iterativos, como o Método de Gauss-Seidel ..
- Em LLSQ a solução é único, mas em NLLSQ pode haver múltiplos mínimos na soma dos quadrados.
- Em NLLSQ estimativas dos erros de parâmetros são tendenciosa, mas em LLSQ eles não são.
Essas diferenças devem ser consideradas sempre que a solução para um problema menos não linear quadrados está sendo procurado.
Mínimos quadrados, análise de regressão e estatísticas
Os métodos de mínimos quadrados e análise de regressão pode parecer métodos diferentes, mas há semelhanças substanciais entre os que são obscurecidas pelo uso de diferentes linguagens utilizadas para descrever os métodos. Ambos os métodos são utilizados para modelar os dados obtidos a partir de observações, e ambos podem utilizar as mesmas técnicas numéricas.
Nas ciências físicas do modelo geralmente tem uma base teórica. Por exemplo, uma mola deve obedecer A lei de Hooke, que afirma que a extensão de uma mola é proporcional à força, F, aplicada a ele.
constitui o modelo, onde F é a variável independente. Para determinar o forçar constante, k, uma série de medidas com forças diferentes irá produzir um conjunto de dados, 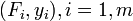 , Onde y i é uma mola de extensão medido. A soma dos quadrados é para ser minimizada
, Onde y i é uma mola de extensão medido. A soma dos quadrados é para ser minimizada
A estimativa dos mínimos quadrados da força constante, k, é dada pela
Aqui, assume-se que a aplicação da força faz com que a mola se expanda e, tendo a constante derivada por mínimos quadrados montagem vigor, a extensão pode ser prevista a partir da lei de Hooke.
Na análise de regressão do modelo é muitas vezes um empírica. Por exemplo, um modelo muito comum é o modelo linear que é usado para comprovar se existe uma relação linear entre a variável dependente e independente. Se uma relação linear como constatadas, as variáveis são disse a ser correlacionados . No entanto, é bem conhecido que a correlação não prova causa, como ambas as variáveis podem ser correlacionados com outros, escondido, variáveis. Por exemplo, existe uma correlação entre as mortes por afogamento e o volume de vendas de sorvete. Tanto o número de pessoas que vão nadar eo volume de gelo aumento de vendas de creme como o clima fica mais quente e pode-se supor que o número de mortes por afogamento correlaciona-se com o número de pessoas que vão nadar.
Em ambos os métodos é geralmente assumido que a variável independente é livre de erro, mas que a variável dependente é sujeita a erro experimental,  .
.
Nesta expressão o valor do modelo é assumido como aproximado do valor real, isto é, o valor que seria observado se havia nenhum erro. Supõe-se que o erro experimental ε é uma variável aleatória com média igual a zero, isto é, que exclui todos os erros de um natureza sistemática. Uma vez que o modelo é apenas uma aproximação ao valor verdadeiro, os resíduos são conceitualmente diferente dos erros. Se a variável independente está sujeito a erros, Total de mínimos quadrados deve ser usado.
A fim de fazer testes estatísticos sobre os resultados é necessário fazer suposições sobre a natureza dos erros experimentais. A hipótese mais comum é que os erros de pertencer a uma distribuição normal . O teorema do limite central suporta a ideia de que esta é uma boa hipótese de, em muitos casos.
- O Gauss-Markov teorema. Em um modelo linear em que os erros têm expectativa de zero, são não correlacionadas e são iguais em desvios , o melhor linear estimador imparcial de qualquer combinação linear das observações, é o seu estimador de mínimos quadrados. "Melhor" significa que os mínimos quadrados estimadores dos parâmetros têm variância mínima. O pressuposto da igualdade de variância é válida quando os erros todos pertencem à mesma distribuição.
- Em um modelo linear, se os erros pertencem a uma distribuição normal dos estimadores de mínimos quadrados são também os estimadores de máxima verossimilhança.
A suposição de que os erros pertencem a uma função de distribuição específica não está confinada à análise de regressão. Na verdade, tais suposições devem ser feitas ao fazer testes estatísticos sobre os parâmetros. Num cálculo dos mínimos quadrados com pesos unitários, ou na regressão linear, a variância na ordem j parâmetro é dada pela
Os limites de confiança pode ser encontrada se a distribuição de probabilidade dos parâmetros é conhecido, ou assumido. Da mesma forma os testes estatísticos sobre os resíduos pode ser feita se a distribuição de probabilidade dos resíduos é conhecida ou presumida. A distribuição de probabilidade de qualquer combinação linear das variáveis dependentes pode ser derivada, se a distribuição de probabilidade de erros experimentais é conhecido ou presumido. Mais comumente, é assumido que os erros experimentais pertencer a uma distribuição normal. Neste caso, muitas vezes é assumido que os parâmetros e os resíduos pertencem a uma distribuição t de student .
A soma do quadrado dos resíduos pode ser expresso como
A matriz 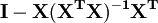 é uma matriz simétrica idempotente de classificação mn. Aqui é um exemplo da utilização do facto de que na teoria de regressão linear. Os valores próprios de uma matriz idempotente são 0 ou 1. Por conseguinte valores próprios desta matriz mn são iguais a 1 e n valores próprios são iguais a zero. Essa é a maioria do trabalho em mostrar que a soma dos resíduos quadrados tem uma distribuição qui-quadrado com graus mn de liberdade.
é uma matriz simétrica idempotente de classificação mn. Aqui é um exemplo da utilização do facto de que na teoria de regressão linear. Os valores próprios de uma matriz idempotente são 0 ou 1. Por conseguinte valores próprios desta matriz mn são iguais a 1 e n valores próprios são iguais a zero. Essa é a maioria do trabalho em mostrar que a soma dos resíduos quadrados tem uma distribuição qui-quadrado com graus mn de liberdade.
Mínimos quadrados ponderados
As expressões dadas acima são baseadas no pressuposto implícito de que todas as medidas são não correlacionadas e têm igual incerteza. O Gauss-Markov teorema mostra que, quando é assim,  é um melhor estimador imparcial linear (AZUL). Se, no entanto, as medidas não estão correlacionados, mas têm diferentes incertezas, deve ser adoptada uma abordagem modificada. Aitken mostraram que, quando uma soma ponderada do quadrado dos resíduos seja minimizada,
é um melhor estimador imparcial linear (AZUL). Se, no entanto, as medidas não estão correlacionados, mas têm diferentes incertezas, deve ser adoptada uma abordagem modificada. Aitken mostraram que, quando uma soma ponderada do quadrado dos resíduos seja minimizada,  é azul se cada peso é igual ao inverso da variância da medição.
é azul se cada peso é igual ao inverso da variância da medição.
As equações de gradiente para este soma dos quadrados são
que, num sistema de mínimos quadrados linear dar as equações normais modificados
ou
Quando os erros de observação não estão correlacionados a matriz de peso, W, é diagonal. Se os erros são correlacionados, a matriz de peso deve ser igual ao inverso do matriz de variância-covariância das observações, mas isso não afeta a expressão de matriz das equações normais e as estimativas dos parâmetros ainda são azuis. Ver Generalizadas mínimos quadrados para obter mais detalhes.
Quando os erros não estão relacionados, é conveniente simplificar os cálculos de factor da matriz como peso 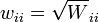 . As equações normais pode então ser escrito como
. As equações normais pode então ser escrito como
Para os sistemas de mínimos quadrados não lineares um argumento similar mostra que as equações normais deve ser modificada como se segue.
Outros métodos
Mínimos quadrados estimativa para modelos lineares é notoriamente não-robusta para discrepantes. Se a distribuição dos valores extremos é distorcido, as estimativas podem ser tendenciosos. Na presença de quaisquer valores aberrantes, as estimativas de mínimos quadrados são ineficientes e pode ser extremamente lenta. Quando ocorrem valores extremos nos dados, métodos de regressão robusta são mais apropriadas.
A técnica de mínimos quadrados parciais está ganhando popularidade em quimiometria e outras disciplinas. É usado quando o modelo é parcialmente conhecido e parcialmente desconhecida.
Os parâmetros de regressão também pode ser estimada pela Métodos Bayesiana. Isto tem as vantagens de que
- intervalos de confiança podem ser produzidos para as estimativas dos parâmetros sem a utilização de aproximações assintótica
- informação prévia podem ser incorporadas na análise.
Na análise de regressão linear,
suponho que sabemos a partir do conhecimento de domínio que  só pode ter um dos valores {-1, 1}, mas não sabemos qual. Nós podemos construir esta informação em análise, escolhendo uma prévia para
só pode ter um dos valores {-1, 1}, mas não sabemos qual. Nós podemos construir esta informação em análise, escolhendo uma prévia para  que é uma distribuição discreta com uma probabilidade de 0,5 a 0,5 e -1 em um. A posterior para
que é uma distribuição discreta com uma probabilidade de 0,5 a 0,5 e -1 em um. A posterior para  Também será uma distribuição discreta em {-1, 1}, mas os pesos de probabilidade serão alteradas para reflectir a evidência a partir dos dados.
Também será uma distribuição discreta em {-1, 1}, mas os pesos de probabilidade serão alteradas para reflectir a evidência a partir dos dados.
Método Lasso
Em alguns contextos um regularizado versão da solução de mínimos quadrados pode ser preferível. O algoritmo de laço, por exemplo, encontra uma solução de mínimos quadrados com a restrição de que 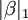 , O L 1 -norm do vector de parâmetros, não é maior do que um determinado valor. Equivalentemente, pode resolver uma minimização irrestrita da pena de mínimos quadrados com
, O L 1 -norm do vector de parâmetros, não é maior do que um determinado valor. Equivalentemente, pode resolver uma minimização irrestrita da pena de mínimos quadrados com 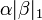 adicionado, onde
adicionado, onde  é uma constante. (Isto é o Lagrangeanos dupla do problema confinado.) Este problema pode ser resolvido usando programação quadrática ou mais geral métodos de otimização convexa. A formulação -regularized L1 é útil em alguns contextos, devido à sua tendência a preferir as soluções com menos valores de parâmetros diferentes de zero, reduzindo efectivamente o número de variáveis em que a solução é dada dependente.
é uma constante. (Isto é o Lagrangeanos dupla do problema confinado.) Este problema pode ser resolvido usando programação quadrática ou mais geral métodos de otimização convexa. A formulação -regularized L1 é útil em alguns contextos, devido à sua tendência a preferir as soluções com menos valores de parâmetros diferentes de zero, reduzindo efectivamente o número de variáveis em que a solução é dada dependente.

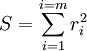
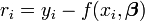

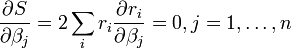
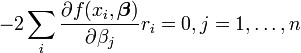
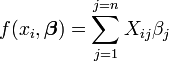
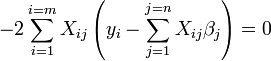
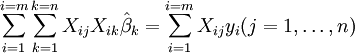
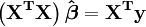
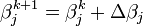
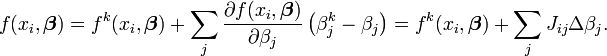
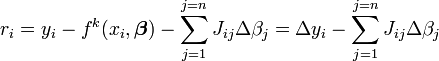
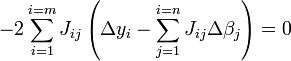
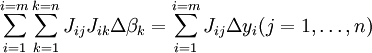
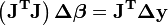
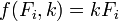
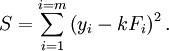
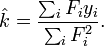
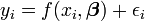
![\ Sigma ^ 2 (\ beta_j) = \ frac {S} {mn} \ left (\ left [X ^ TX \ right] ^ {- 1} \ right) _ {} jj.](../../images/203/20359.png)