
Regressão linear
Sobre este escolas selecção Wikipedia
Crianças SOS, uma instituição de caridade educação , organizou esta selecção. Uma boa maneira de ajudar outras crianças é por patrocinar uma criança
A regressão linear é uma forma de análise de regressão em que os dados de observação são modelados por um dos mínimos quadrados que é uma função combinação linear dos parâmetros do modelo e depende de uma ou mais variáveis independentes. Na regressão linear simples a função de modelo representa uma linha reta. Os resultados dos dados que cabem estão sujeitas à análise estatística.
Definições
Os dados consistem de valores de m 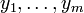 feita a partir de observações da variável dependente ( variável de resposta)
feita a partir de observações da variável dependente ( variável de resposta)  . A variável dependente é sujeita a erro. Este erro é assumido como sendo variável aleatória , com uma média de zero. O erro sistemático (eg média ≠ 0) pode estar presente, mas o seu tratamento está fora do âmbito da análise de regressão. A variável independente ( variável explicativa)
. A variável dependente é sujeita a erro. Este erro é assumido como sendo variável aleatória , com uma média de zero. O erro sistemático (eg média ≠ 0) pode estar presente, mas o seu tratamento está fora do âmbito da análise de regressão. A variável independente ( variável explicativa)  , É livre de erros. Se assim não for, modelagem deve ser feito usando erros nas variáveis técnicas modelo. As variáveis independentes são também chamados de regressores, variáveis exógenas, variáveis de entrada e variáveis de previsão. Na regressão linear simples, o modelo de dados é escrito como
, É livre de erros. Se assim não for, modelagem deve ser feito usando erros nas variáveis técnicas modelo. As variáveis independentes são também chamados de regressores, variáveis exógenas, variáveis de entrada e variáveis de previsão. Na regressão linear simples, o modelo de dados é escrito como
onde  é um erro observacional.
é um erro observacional. 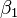 (Intercepção) e
(Intercepção) e 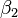 (Declive) são os parâmetros do modelo. Em geral, existem parâmetros n,
(Declive) são os parâmetros do modelo. Em geral, existem parâmetros n, 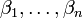 e o modelo pode ser escrito como
e o modelo pode ser escrito como
onde os coeficientes 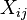 são constantes ou funções da variável independente, x. Os modelos que não estejam em conformidade com esta especificação deve ser tratado por de regressão não-linear.
são constantes ou funções da variável independente, x. Os modelos que não estejam em conformidade com esta especificação deve ser tratado por de regressão não-linear.
A menos que indicado de outro modo, assume-se que os erros de observação são uncorrelated e pertencem a uma distribuição normal . Isso, ou outra hipótese, é usado quando a realização de testes estatísticos sobre os resultados da regressão. Uma formulação equivalente de regressão linear simples que mostra explicitamente a regressão linear como um modelo de esperança condicional pode ser dada como
O distribuição condicional de y x dado é uma transformação linear do distribuição do termo de erro.
Convenções de notação e de nomeação
- Escalares e vectores são denotados por letras minúsculas.
- Matrizes são indicados por letras maiúsculas.
- Os parâmetros são indicados por letras gregas.
- Vetores e matrizes são indicados por letras em negrito.
- Um parâmetro com um chapéu, como
 , Indica um estimador de parâmetro.
, Indica um estimador de parâmetro.
Análise de mínimos quadrados
O primeiro objectivo da análise de regressão é a que melhor se ajusta aos dados por ajuste dos parâmetros do modelo. Dos diferentes critérios que podem ser usados para definir o que constitui um melhor ajuste, o critério de mínimos quadrados é muito poderoso. A função objetivo, S, é definido como a soma dos resíduos quadrados, r i
onde cada residual é a diferença entre o valor observado e o valor calculado pelo modelo:
O melhor ajuste é obtido quando a S, a soma do quadrado dos resíduos, é minimizada. Sujeito a certas condições, os parâmetros, em seguida, tem mínimo variância ( Teorema de Gauss-Markov) e também pode representar um solução de probabilidade máxima para o problema de otimização.
A partir da teoria de mínimos quadrados lineares, os parâmetros são estimadores encontrada resolvendo as equações normais
Em notação matricial, estas equações são escritas como
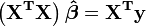 ,
,
E, assim, quando a matriz 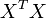 não é singular:
não é singular:
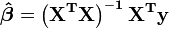 ,
,
Especificamente, para a montagem em linha recta, isto é mostrado em montagem linha reta.
Estatísticas de regressão
O segundo objectivo da regressão é a análise estatística dos resultados de encaixe dados.
Denote por 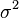 a variância do termo de erro
a variância do termo de erro  (De modo que
(De modo que 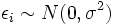 para cada
para cada  ). Uma estimativa imparcial de
). Uma estimativa imparcial de 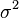 é dado pela
é dado pela
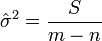 .
.
A relação entre a estimativa eo valor verdadeiro é:
onde 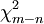 tem distribuição qui-quadrado com
tem distribuição qui-quadrado com 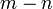 graus de liberdade.
graus de liberdade.
A aplicação deste teste requer que 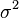 , A variação de uma unidade de observação de peso, ser estimada. Se o
, A variação de uma unidade de observação de peso, ser estimada. Se o  teste é passado, os dados podem ser dito para ser instalado no interior de erro de observação.
teste é passado, os dados podem ser dito para ser instalado no interior de erro de observação.
A solução para as equações normais pode ser escrito como
Isto mostra que os parâmetros são estimadores combinações lineares da variável dependente. Daqui resulta que, se os erros de observação são normalmente distribuídos, os estimadores dos parâmetros irá pertencer a uma distribuição t de Student com 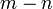 graus de liberdade. O desvio padrão em um estimador parâmetro é dada pela
graus de liberdade. O desvio padrão em um estimador parâmetro é dada pela
O 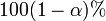 intervalo de confiança para o parâmetro,
intervalo de confiança para o parâmetro,  , É calculado como segue:
, É calculado como segue:
Os resíduos podem ser expressos como
A matriz 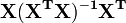 é conhecido como o matriz chapéu e tem a propriedade de que é útil idempotent. Usando esta propriedade pode ser mostrado que, se os erros são normalmente distribuídos, os resíduos seguirá uma distribuição t de Student com
é conhecido como o matriz chapéu e tem a propriedade de que é útil idempotent. Usando esta propriedade pode ser mostrado que, se os erros são normalmente distribuídos, os resíduos seguirá uma distribuição t de Student com 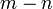 graus de liberdade. Studentized resíduos são úteis em testes para discrepantes.
graus de liberdade. Studentized resíduos são úteis em testes para discrepantes.
Dado um valor da variável independente, x d, a resposta é calculada como previsto
Escrevendo os elementos 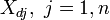 como
como  , O
, O 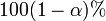 significa intervalo de confiança de resposta é dada para a predição, usando teoria de propagação de erro, por:
significa intervalo de confiança de resposta é dada para a predição, usando teoria de propagação de erro, por:
O 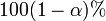 intervalos de confiança de resposta previstos para os dados são dados por:
intervalos de confiança de resposta previstos para os dados são dados por:
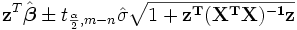 .
.
Caso linear
No caso em que a fórmula para ser montado é uma linha recta, 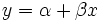 , As equações são normais
, As equações são normais
onde todos os somatórios são a partir de i = 1 a I = m. Daí, por Regra de Cramer,
onde
A matriz de covariância é
O significa intervalo de confiança de resposta é dada por
O intervalo de confiança de resposta prevista é dada pela
A análise de variância
A análise de variância é semelhante ao ANOVA em que a soma dos residuais quadrados é dividido em dois componentes. A soma de regressão dos quadrados (ou soma do quadrado dos resíduos) SSR (também comumente chamado RSS) é dada por:
onde  e L é um N em 1 unidade vector (isto é, cada elemento é 1). Note-se que os termos
e L é um N em 1 unidade vector (isto é, cada elemento é 1). Note-se que os termos 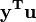 e
e 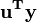 são ambos equivalente a
são ambos equivalente a 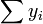 , E assim o termo
, E assim o termo 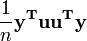 é equivalente a
é equivalente a 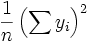 .
.
O erro (ou inexplicável) soma dos quadrados ESS é dada por:
A soma total dos quadrados TSS é dada por
Coeficiente de regressão de Pearson, R ² é então dado como
Exemplo
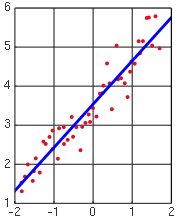
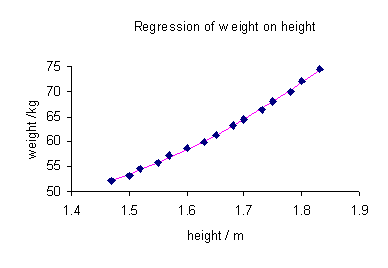
Para ilustrar as diferentes metas de regressão, nós damos um exemplo. O seguinte conjunto de dados dá as alturas e pesos médios para as mulheres americanas com idades entre 30-39 (fonte: The World Almanac e livro de fatos, 1975).
Altura / m 1.47 1,5 1.52 1.55 1.57 1.60 1.63 1.65 1.68 1,7 1.73 1.75 1.78 1,8 1.83 / Kg de peso 52.21 53,12 54,48 55,84 57,2 58,57 59,93 61,29 63.11 64,47 66,28 68,1 69,92 72,19 74,46
Um lote de peso contra a altura (ver abaixo) mostra que não pode ser simulada por uma linha recta, de modo que se uma regressão realizadas pelo modelo de dados por uma parábola.
onde a variável dependente, y, é o peso e a variável independente, x é a altura.
Coloque os coeficientes,  , Dos parâmetros para o i-ésimo observação da i-ésima linha da matriz X.
, Dos parâmetros para o i-ésimo observação da i-ésima linha da matriz X.

Os valores dos parâmetros são encontrados resolvendo as equações normais
Elemento ij da matriz equação normal, 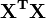 é formado pela soma dos produtos de coluna i e coluna j de X.
é formado pela soma dos produtos de coluna i e coluna j de X.
Elemento i do lado vetor da mão direita 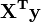 é formado pela soma dos produtos de i X de coluna com a coluna de valores de variáveis independentes.
é formado pela soma dos produtos de i X de coluna com a coluna de valores de variáveis independentes.
Assim, as equações são normais
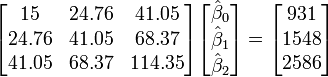
 (Valor
(Valor 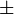 desvio padrão)
desvio padrão) 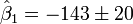

Os valores calculados são dados pela
Os dados observados e calculados são traçados em conjunto e os resíduos, 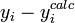 , São calculados e plotados. Os desvios padrão são calculados usando a soma dos quadrados,
, São calculados e plotados. Os desvios padrão são calculados usando a soma dos quadrados, 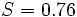 .
.
Os intervalos de confiança são calculados usando:
com  = 5%,
= 5%, 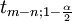 = 2,2. Portanto, podemos dizer que o 95% intervalos de confiança são:
= 2,2. Portanto, podemos dizer que o 95% intervalos de confiança são:
Verificando pressupostos do modelo
Os pressupostos do modelo são verificados através do cálculo dos resíduos e traçando-los. Os seguintes lotes pode ser construído de modo a testar a validade das hipóteses:
- Residuais contra a variável explicativa, conforme ilustrado acima.
- A tempo série gráfico dos resíduos, ou seja, traçando os resíduos como uma função do tempo.
- Residuais contra os valores embutidos,
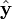 .
. - Resíduos em relação à anterior residual.
- Um gráfico de probabilidade normal dos resíduos para testar a normalidade. Os pontos devem estar em linha reta.
Não deve haver nenhum padrão perceptível para os dados em todos, mas o último lote
Verificando modelo validade
A validade do modelo pode ser verificada utilizando qualquer um dos métodos que se seguem:
- Usando o intervalo de confiança para cada um dos parâmetros,
 . Se o intervalo de confiança inclui a 0, em seguida, o parâmetro pode ser removida do modelo. Idealmente, uma nova análise de regressão excluindo esse parâmetro terá de ser realizada e continuou até que não haja mais parâmetros para remover.
. Se o intervalo de confiança inclui a 0, em seguida, o parâmetro pode ser removida do modelo. Idealmente, uma nova análise de regressão excluindo esse parâmetro terá de ser realizada e continuou até que não haja mais parâmetros para remover. - Ao montar uma linha reta, calcule o coeficiente de regressão de Pearson. Quanto mais próximo o valor é 1; o melhor é a regressão. Este coeficiente indica qual a fracção do comportamento observado pode ser explicada pelas variáveis dadas.
- Examinando os intervalos de confiança de observação e previsão. Quanto menor forem, melhor.
- Calculando a F-estatísticas.
Outros procedimentos
Mínimos quadrados ponderados
Mínimos quadrados ponderados é uma generalização do método dos mínimos quadrados, utilizado quando os erros observacionais têm variância desigual.
Com erros nas variáveis de modelo
Com erros nas variáveis do modelo ou total de mínimos quadrados quando a variável independente é sujeita a erro
Modelo linear generalizado
Modelo linear generalizado é usado quando a função de distribuição dos erros não é uma distribuição normal. Exemplos incluem distribuição exponencial , distribuição gama, Distribuição Inverse Gaussian, distribuição de Poisson , a distribuição binomial , distribuição multinomial
Regressão robusta
Uma série de abordagens alternativas para o cálculo de parâmetros da regressão estão incluídos na categoria conhecida como regressão robusta. Uma técnica minimiza o significativo erro absoluto, ou alguma outra função dos resíduos, em vez do quadrado médio do erro como na regressão linear. Regressão robusta é computacionalmente muito mais intensa do que a regressão linear e é um pouco mais difícil de implementar também. Embora as estimativas de mínimos quadrados não são muito sensíveis a quebrar a normalidade da suposição de erros, isso não é verdade quando a variância ou média da distribuição de erro não é limitado, ou quando um analista que pode identificar valores extremos não está disponível.
Entre Usuários Stata, regressão robusta é frequentemente tomado para significar regressão linear com Huber-White estimativas de erro padrão devido às convenções de nomenclatura para os comandos de regressão. Este procedimento relaxa o pressuposto de homocedasticidade para a variância estima somente; os preditores são ainda Mínimos Quadrados Ordinários (MQO) estimativas. Este ocasionalmente leva à confusão; Usuários Stata, por vezes, acreditam que a regressão linear é um método robusto quando essa opção for usada, embora, na verdade, não é robusta no sentido de outlier-resistência.
Aplicações de regressão linear
A regressão linear é amplamente utilizado em ciências biológicas, comportamentais e sociais para descrever relações entre as variáveis. É considerado como um dos mais importantes instrumentos utilizados nestas disciplinas.
A linha de tendência
Uma linha de tendência representa uma tendência, o movimento de longo prazo em dados de séries temporais após outros componentes foram contabilizados. Ele diz se um conjunto de dados específico (dizer PIB, os preços do petróleo ou os preços das ações) aumentaram ou diminuíram durante o período de tempo. Uma linha de tendência pode ser simplesmente puxado por olho através de um conjunto de pontos de dados, mas mais propriamente a sua posição e inclinação é calculado utilizando técnicas estatísticas como a regressão linear. Linhas de tendência tipicamente são linhas rectas, embora algumas variações usar polinómios de grau superior, dependendo do grau de curvatura desejada na linha.
Linhas de tendência são por vezes utilizados em análise de negócios para mostrar alterações nos dados ao longo do tempo. Isto tem a vantagem de ser simples. Linhas de tendência são muitas vezes utilizados para argumentar que uma determinada ação ou evento (como treinamento, ou uma campanha publicitária) causou mudanças observadas em um ponto no tempo. Esta é uma técnica simples, e não requer um grupo de controlo, desenho experimental, ou uma técnica de análise sofisticado. No entanto, sofre de uma falta de eficácia científica nos casos em que outros potenciais alterações podem afectar os dados.
Medicina
Como um exemplo, evidências iniciais relativas tabagismo na mortalidade e morbidade veio de estudos que empregam regressão. Pesquisadores geralmente incluem diversas variáveis em sua análise de regressão em um esforço para remover os fatores que possam produzir correlações espúrias. Para o exemplo tabagismo, os pesquisadores podem incluir status sócio-econômico, além de fumar para garantir que qualquer efeito do tabagismo sobre a mortalidade observada não é devido a algum efeito da educação ou renda. No entanto, nunca é possível incluir todas as possíveis variáveis de confusão em uma regressão estudo empregando. Para o exemplo de fumar, um gene hipotético pode aumentar a mortalidade e também levar as pessoas a fumar mais. Por esta razão, ensaios clínicos randomizados são considerados mais confiáveis do que uma análise de regressão.
Finanças
O CAPM usa a regressão linear, bem como o conceito de Beta para analisar e quantificar o risco sistemático de um investimento. Isso vem diretamente do Coeficiente Beta do modelo de regressão linear que relaciona o retorno sobre o investimento para o retorno de todos os ativos de risco.
Regressão pode não ser a forma apropriada para estimar beta em finanças, uma vez que é suposto fornecer a volatilidade de um investimento em relação à volatilidade do mercado como um todo. Isto iria exigir que ambas as variáveis ser tratados da mesma forma, quando a estimativa do declive. Considerando trata de regressão toda a variabilidade como sendo o investimento retorna variável, ou seja, considera apenas os resíduos na variável dependente.
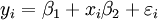
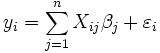

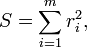

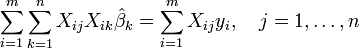
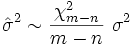
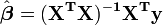
![\ Hat \ sigma_j = \ sqrt {\ frac {S} {mn} \ left [\ mathbf {(X ^ TX)} ^ {- 1} \ right] _ {}} jj](../../images/216/21697.png)

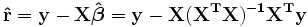
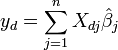

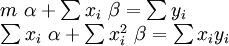
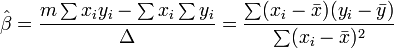


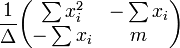

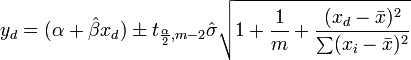
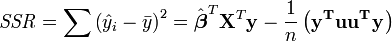
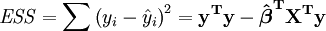


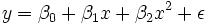
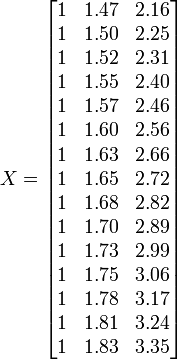
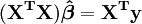
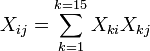
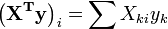

![[\ Hat {\ beta_j} - \ sigma_j t_ {mn; 1- \ frac {\ alpha} {2}}; \ hat {\ beta_j} + \ sigma_j t_ {mn; 1- \ frac {\ alpha} {2 }}]](../../images/217/21747.png)
![\ Beta_0 \ in [92.9,164.7]](../../images/217/21749.png)
![\ Beta_1 \ in [-186,8, -99,5]](../../images/217/21750.png)
![\ Beta_2 \ in [48.7,75.2]](../../images/217/21751.png)
