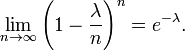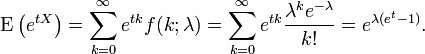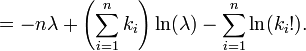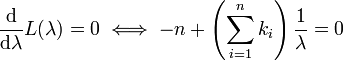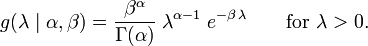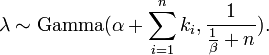Distribuição de Poisson

Assuntos Relacionados: Matemática

Sobre este escolas selecção Wikipedia

Crianças SOS, uma instituição de caridade educação , organizou esta selecção. Veja http://www.soschildren.org/sponsor-a-child para saber mais sobre apadrinhamento de crianças.

Poisson
Função massa de probabilidade O eixo horizontal é o índice k. A função é definida apenas em valores inteiros de k. As linhas de conexão são apenas guias para o olho e não indicam continuidade.
Função de distribuição cumulativa O eixo horizontal é o índice k.
Parâmetros	$\ Lambda \ in (0, \ infty)$
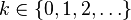Apoio	$k \ in \ {0,1,2, \ ldots \}$
PMF	$\ Frac {e ^ {- \ lambda} \ lambda ^} {k k!} \!$
CDF	$\ Frac {\ Gamma (\ lfloor k + 1 \ rfloor, \ lambda)} {\ lfloor k \ rfloor!} \! \ Texto {for} k \ ge 0$ (Onde $\ Gamma (X, Y)$ é o Função gama incompleta)
Significar	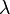$\ Lambda \,$
Mediano	$\ Text {normalmente cerca} \ lfloor \ lambda + 1 / 3-0,02 / \ lambda \ rfloor$
Modo	$\ Lfloor \ lambda \ rfloor$ e $\ Lambda-1$ se $\ Lambda$ é um número inteiro
Variação	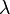$\ Lambda \,$
Assimetria	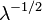$\ Lambda ^ {- 1/2} \,$
Ex. curtose	$\ Lambda ^ {- 1} \,$
Entropy	$\ Lambda [1 \ -! \ \ Ln (\ lambda)]! \ + \ E ^ {- \ lambda} \ sum_ {k = 0} ^ \ infty \ frac {\ lambda ^ k \ ln (k! )} {k!}$ (Para grande $\ Lambda$ ) $\ Frac {1} {2} \ log (2 \ pi e \ lambda) - \ frac {1} {12 \ lambda} - \ frac {1} {24 \ lambda ^ 2} - \ frac {19} {360 \ lambda ^ 3} + O (\ frac {1} {\ lambda ^ 4})$
MGF	$\ Exp (\ lambda (e ^ t-1)) \,$
CF	$\ Exp (\ lambda (e ^ {o} -1)) \,$

Em teoria da probabilidade e estatística , a distribuição de Poisson é uma distribuição de probabilidade discreta que expressa a probabilidade de uma série de eventos que ocorrem em um período fixo de tempo, se esses eventos ocorrem com uma taxa média conhecida e independentemente do tempo desde o último evento. A distribuição de Poisson, também pode ser utilizado para o número de eventos em outros intervalos determinados, tais como a distância, a área ou volume.

A distribuição foi descoberto pela Siméon-Denis Poisson ( 1781 - 1840 ) e publicada, com sua teoria da probabilidade, em 1838, em sua obra Recherches sur la probabilité des jugements en matières criminelles et matière civile ("Pesquisa sobre a probabilidade de decisões em matéria penal e civil") . O trabalho se concentrou em certas variáveis aleatórias N que contam, entre outras coisas, um número de ocorrências discretas (algumas vezes chamado de "chegadas") que ocorrem durante um tempo -interval de determinado comprimento. Se o número esperado de ocorrências neste intervalo é λ, então a probabilidade de que não são exactamente ocorrências k (sendo k um não-negativo inteiro , k = 0, 1, 2, ...) é igual a

$f (k, \ lambda) = \ frac {\ lambda ^ ke ^ {- \ lambda}} {k!}, \, \!$

onde

e é a base do logaritmo natural (e = 2,71828 ...)
k é o número de ocorrências de um evento - a probabilidade de que é dado pela função
k! é o fatorial de k
λ é um positivo número real , igual ao número esperado de ocorrências que ocorrem durante o intervalo dado. Por exemplo, se os eventos ocorrem em média a cada quatro minutos, e você está interessado no número de eventos que ocorrem em um intervalo de 10 minutos, você usaria como modelo de uma distribuição de Poisson com λ = 10/4 = 2,5.

Como uma função de k, esta é a função massa de probabilidade. A distribuição de Poisson pode ser derivada como um caso limite da distribuição binomial .

A distribuição de Poisson pode ser aplicada a sistemas com um grande número de possíveis eventos, cada um dos quais é rara. Um exemplo clássico é o decaimento nuclear de átomos.

A distribuição de Poisson é por vezes chamado de Poissonian, análogo ao gaussiana para um termo de Gauss ou distribuição normal .

Ruído Poisson e caracterizar pequenas ocorrências

O parâmetro λ é não só o significativo número de ocorrências 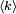$\ Scriptstyle \ langle k \ rangle$ , Mas também a sua variância $\ Scriptstyle \ sigma_k ^ 2 \ \ stackrel {\ mathrm {def}} {} = \ \ langle k ^ {2} \ rangle - \ langle k \ rangle ^ {2}$ (Ver quadro). Assim, o número de ocorrências observadas flutua sobre sua média λ com um desvio-padrão $\ Scriptstyle \ sigma_ {k} \, = \, \ sqrt {\ lambda}$ . Estas flutuações são indicadas como Poisson ou ruído (particularmente em eletrônica) como Filmado ruído.

A correlação da média e desvio padrão, na contagem de ocorrências discretas independentes é útil cientificamente. Ao monitorizar como as flutuações variar com a média do sinal, pode-se estimar a contribuição de uma ocorrência única, mesmo que a contribuição é muito pequeno para ser detectado directamente. Por exemplo, a carga de e sobre um electrão pode ser estimado por meio da correlação da magnitude de um corrente eléctrica com o seu Filmado ruído. Se n electrões passam um ponto num determinado tempo t em média, a média atual é I = pt / t; uma vez que as flutuações de corrente deve ser da ordem $\ Scriptstyle \ sigma_ {I} = e \ sqrt {N / t \}$ (Isto é, a variação do processo de Poisson), a carga e pode ser calculada a partir da razão $\ Scriptstyle \ sigma_ {I} ^ {2} / I$ . Um exemplo cotidiano é a granulação que aparece como fotografias são ampliadas; a granulação é devido a flutuações de Poisson no número de redução de prata grãos, não para os próprios grãos individuais. Ao correlacionar a granulação com o grau de ampliação, pode-se estimar a contribuição de uma grãos individuais (que de resto é demasiado pequena para ser vista desarmada). Muitas outras aplicações moleculares de ruído de Poisson têm sido desenvolvidos, por exemplo, a estimativa do número de densidade moléculas receptoras em um membrana celular.

$\ Pr (N_t = k) = f (k; \ lambda t) = \ frac {e ^ {- \ lambda t} (\ lambda t) ^ k} {k!}, \, \!$

Distribuições relacionados

Se $X_1 \ sim \ mathrm {Pois} (\ lambda_1) \,$ e $X_2 \ sim \ mathrm {Pois} (\ lambda_2) \,$ em seguida, a diferença $Y = X_1 - X_2$ segue uma Distribuição Skellam.
Se $X_1 \ sim \ mathrm {Pois} (\ lambda_1) \,$ e $X_2 \ sim \ mathrm {Pois} (\ lambda_2) \,$ são independentes, e $Y = X_1 + X_2$ , Então a distribuição de $X_1$ em condicional $Y = y$ é um binomial . Especificamente, $X_1 | (Y = y) \ sim \ mathrm {Binom} (y, \ lambda_1 / (\ lambda_1 + \ lambda_2)) \,$ . De modo mais geral, se X _1, X _2, ..., X _n são variáveis aleatórias de Poisson com parâmetros λ _1, λ _2, ..., _n, em seguida, λ $X_i \ left | \ sum_ {j = 1} ^ n X_j \ right. \ Sim \ mathrm {Binom} \ left (\ sum_ {j = 1} ^ nX_j, \ frac {\ lambda_i} {\ sum_ {j = 1} ^ n \ lambda_j} \ right)$
A distribuição de Poisson pode ser derivada como um caso limite para a distribuição binomial como o número de ensaios vai para o infinito e o número esperado de sucessos permanece fixo. Por isso, pode ser usado como uma aproximação da distribuição binomial se n for suficientemente grande e p é suficientemente pequena. Não é regra geral indicando que a distribuição de Poisson é uma boa aproximação de distribuição binomial se n for pelo menos 20 e p é menor do que ou igual a 0,05. De acordo com esta regra, a aproximação é excelente se n ≥ 100 e ≤ 10 np.
Para valores suficientemente grandes de λ, (digamos λ> 1000), a distribuição normal com média λ, e variância λ, é uma excelente aproximação para a distribuição de Poisson. Se λ é maior do que cerca de 10, então a distribuição normal é uma boa aproximação se um adequado correcção de continuidade é efectuada, isto é, P (X ≤ x), onde (letras minúsculas) x é um número inteiro não negativo, é substituído por P (X ≤ x + 0,5).

$F_ \ mathrm {} Poisson (x; \ lambda) \ approx F_ \ mathrm {Normal} (x; \ mu = \ lambda, \ sigma ^ 2 = \ lambda) \,$

Se o número de entradas em um determinado tempo segue a distribuição de Poisson, com média = $\ Lambda$ , Então os comprimentos dos tempos entre chegadas seguir a distribuição exponencial , com taxa $1 / \ lambda$ .

Ocorrência

A distribuição de Poisson surge em ligação com Processos de Poisson. Ele aplica-se a vários fenómenos de natureza discreta (isto é, aqueles que podem acontecer 0, 1, 2, 3, ... vezes, durante um determinado período de tempo ou numa determinada área) sempre que a probabilidade do fenómeno acontece é constante em tempo ou espaço. Exemplos de eventos que podem ser modeladas como uma distribuição de Poisson incluem:

O número de carros que passam por um determinado ponto em uma estrada (suficientemente longe do semáforo) durante um determinado período de tempo.
O número de erros de ortografia ao digitar um faz uma única página.
O número de chamadas de telefone a uma call center por minuto.
O número de vezes que um servidor web é acessada por minuto.
O número de atropelamentos (animais mortos) encontrados por unidade de comprimento da estrada.
O número de mutações em um determinado trecho de ADN depois de uma certa quantidade de radiação.
O número de instáveis núcleos que deteriorado dentro de um determinado período de tempo em um pedaço de substância radioactiva. A radioactividade da substância irá enfraquecer com o tempo, de modo que o intervalo de tempo total utilizado no modelo deve ser significativamente menor do que o tempo de vida da substância quer dizer.
O número de pinheiros por unidade de área de floresta mista.
O número de estrelas de um dado volume de espaço.
O número de soldados mortos por cavalo-chutes cada ano em cada corpo no Cavalaria prussiana. Este exemplo foi feito famoso por um livro de Ladislaus Josephovich Bortkiewicz ( 1868 - 1931 ).
A distribuição das células receptoras visuais na retina do humano olho .
O número de lâmpadas que queimam em um determinado período de tempo.
O número de vírus capazes de infectar uma célula em cultura de células.
O número de células-tronco hematopoiéticas, em uma amostra de células de medula óssea não fraccionadas.
O número de invenções de um inventor sobre sua carreira.
O número de partículas que "dispersão" fora de um alvo numa experiência física energia nuclear ou alta.

[Nota: estão relacionados reciprocamente-os intervalos entre sucessivas eventos de Poisson, seguindo a distribuição exponencial . Por exemplo, a vida útil de uma lâmpada, ou o tempo de espera entre autocarros.]

Como é que esta distribuição surgem? - A lei de eventos raros

Em vários dos exemplos exemplo-para cima, o número de mutações em uma determinada sequência de ADN a ser contados os eventos são, na verdade, os resultados de ensaios separados, e seria mais precisamente ser modeladas utilizando a distribuição binomial . No entanto, a distribuição binomial com parâmetros n e λ / n, ou seja, a distribuição de probabilidade do número de sucessos em n tentativas, com probabilidade λ / n de sucesso em cada tentativa, se aproxima da distribuição de Poisson com valor esperado λ como n se aproxima do infinito . Este limite é por vezes conhecida como a lei de eventos raros, embora este nome pode ser enganosa, porque os eventos em um processo de Poisson não precisa ser raro (o número de chamadas telefónicas a uma central telefónica ocupado em uma hora segue uma distribuição de Poisson, mas esses eventos não seria considerada rara). Ele fornece um meio pelo qual a aproximar variáveis aleatórias usando a distribuição de Poisson, em vez de a distribuição binomial mais-pesado.

Aqui estão os detalhes. Em primeiro lugar, lembre-se de cálculo que

$\ Lim_ {n \ to \ infty} \ left (1 - {\ lambda \ over n} \ right) ^ n = e ^ {- \ lambda}.$

Seja p = λ / n. Então nós temos

$\ Lim_ {n \ to \ infty} \ Pr (X = k) = \ lim_ {n \ to \ infty} {n \ escolher k} k ^ p (1-p) ^ {nk} = \ lim_ {n \ to \ infty} {n! ! \ Over (nk) k} \ left ({\ lambda \ over n} \ right) ^ k \ left (1 - {\ lambda \ over n} \ right) ^ {nk}$

$= \ Lim_ {n \ to \ infty} \ underbrace {\ left ({n \ n} sobre \ right) \ left ({n-1 \ over n} \ right) \ left ({n-2 \ over n} \ right) \ cdots \ left ({n-k + 1 \ over n} \ right)} \ \ underbrace {\ left ({\ lambda ^ k \ over k!} \ right)} \ \ underbrace {\ left ( 1 - {\ lambda \ over n} \ right) ^ n} \ \ underbrace {\ left (1 - {\ lambda \ over n} \ right) ^ {- k}}$

Como n se aproxima do ∞, a expressão em relação ao primeiro underbrace se aproxima de 1; o segundo permanece constante desde "n" não aparece nele em tudo; o terceiro e se aproxima ^-λ; e a quarta expressão se aproxima de 1.

Por conseguinte, o limite é de

${\ Lambda ^ k e ^ {- \ lambda} \ over k!} \, \.!$

Em termos mais gerais, sempre que uma sequência de variáveis aleatórias binomial com parâmetros n e p _n é tal que

$\ Lim_ {n \ rightarrow \ infty} np_n = \ lambda,$

a sequência converge em distribuição para uma variável aleatória Poisson com média λ (ver, por exemplo, lei de eventos raros).

Propriedades

O valor esperado de uma variável aleatório de Poisson-distribuído é igual a λ e assim é a sua variância . Quanto maior momentos da distribuição de Poisson é Polinômios Touchard em λ, cujos coeficientes têm uma combinatória significado. Na verdade, quando o valor esperado da distribuição de Poisson é 1, então A fórmula de Dobinski diz que o n-ésimo momento é igual ao número de partições de um conjunto de tamanho n.

O modo de uma variável aleatória com uma distribuição de Poisson com não-inteiro λ é igual a $\ Scriptstyle \ lfloor \ lambda \ rfloor$ , Que é o maior número inteiro inferior ou igual a λ. Esta é também escrito como andar (λ). Quando λ é um número inteiro positivo, os modos são λ e λ - 1.

Somas de variáveis aleatórias de Poisson distribuídos:

Se $X_i \ sim \ mathrm {} Poi (\ lambda_i) \,$ seguem uma distribuição de Poisson com parâmetro $\ Lambda_i \,$ e $X_i$ são independente, em seguida $Y = \ sum_ {i = 1} ^ N x_i \ sim \ mathrm {Poi} \ left (\ sum_ {i = 1} ^ N \ lambda_i \ right) \,$ também segue uma distribuição de Poisson, cujo parâmetro é a soma dos parâmetros de componentes.

O função momento de geração da distribuição de Poisson com λ valor esperado é

$\ Mathrm {E} \ left (e ^ {tX} \ right) = \ sum_ {k = 0} ^ \ infty e ^ {tk} f (k; \ lambda) = \ sum_ {k = 0} ^ \ infty e ^ {tk} {\ lambda ^ ke ^ {- \ lambda} \ over k} = e ^ {\ lambda (e ^ t-1)}.$

Todos os cumulantes da distribuição de Poisson é igual ao valor λ esperado. O n-ésimo fatorial momento da distribuição de Poisson é λ ^n.

As distribuições são Poisson infinitamente divisível distribuições de probabilidade.

O dirigidos Kullback-Leibler divergência entre Poi (λ ₀₎ e Poi (λ) é dada por

$\ Delta (\ lambda || \ lambda_0) = \ lambda \ left (1 - \ frac {\ lambda_0} {\ lambda} + \ frac {\ lambda_0} {\ lambda} \ log \ frac {\ lambda_0} {\ lambda } \ right).$

Geração de Poisson distribuído variáveis aleatórias

Uma maneira simples de gerar números aleatórios distribuição de Poisson é dada por Knuth , ver referências abaixo.

 poisson algoritmo número aleatório (Knuth):
     nisso:
          Seja L ← e ^-λ, k ← 0 e p ← 1.
     Faz:
          k ← k + 1.
          Gerar número aleatório uniforme u em [0,1] e deixe p ← p × u.
     enquanto p ≥ L.
     retornar k - 1.

Embora simples, a complexidade é linear em λ. Há muitos outros algoritmos para superar isso. Alguns são dadas em Ahrens & Dieter, ver referências abaixo.

Estimação de parâmetros

Máxima verossimilhança

Dada uma amostra de n valores medidos k _i desejamos para estimar o valor do parâmetro λ da população de Poisson a partir do qual a amostra foi tirada. Para calcular o valor de máxima verossimilhança, formamos a função de log-verossimilhança

$L (\ lambda) = \ ln \ Prod_ {i = 1} ^ nf (k_i \ mid \ lambda) \!$

$= \ Sum_ {i = 1} ^ n \ ln \ \ left (\ frac {e ^ {- \ lambda} \ lambda ^ {}} {k_i K_i!} \ Right)! \!$

$-n = \ Lambda + \ left (\ sum_ {i = 1} ^ n k_i \ right) \ ln (\ lambda) - \ sum_ {i = 1} ^ n \ ln (k_i!). \!$

Tome a derivada de L em relação a λ e compará-lo a zero:

$\ Frac {\ mathrm {d}} {\ mathrm {d} \ lambda} L (\ lambda) = 0 \ sse -n + \ left (\ sum_ {i = 1} ^ n k_i \ right) \ frac {1 } {\ lambda} = 0 \!$

Resolvendo para λ produz a estimativa de probabilidade máxima de λ:

$\ Widehat {\ lambda} _ \ mathrm {MLE} = \ frac {1} {n} \ sum_ {i = 1} ^ n k_i. \!$

Uma vez que cada observação tem expectativa λ assim que isso média da amostra. Por isso, é um estimador imparcial de λ. É também um estimador eficiente, ou seja, a sua variância estimativa atinge o Cramér-Rao limite inferior (CRLB).

Inferência Bayesiana

Em inferência bayesiana , o conjugado antes para o parâmetro da velocidade de λ da distribuição de Poisson é a Distribuição Gama. Deixar

$\ Lambda \ sim \ mathrm {Gamma} (\ alpha, \ beta) \!$

denotam que λ é distribuído de acordo com a Gamma Densidade g parametrizada em termos de um moldar parâmetro α e um inverso β parâmetro de escala:

$g (\ lambda \ mid \ alpha, \ beta) = \ frac {\ beta ^ {\ alpha}} {\ Gamma (\ alpha)} \; \ Lambda ^ {\ alpha-1} \; e ^ {- \ beta \, \ lambda} \ qquad \ mbox {para} \ \ lambda> 0 \, \ !.$

Em seguida, dada a mesma amostra de N valores de k _i medido como antes, e uma prévia de Gama (α, β), a distribuição a posteriori é

$\ Lambda \ sim \ mathrm {Gamma} (\ alpha + \ sum_ {i = 1} ^ n k_i, \ frac {1} {\ frac {1} {\ beta}} + n). \!$

A posterior dizer E [λ] aborda a estimativa de probabilidade máxima 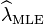$\ Widehat {\ lambda} _ \ mathrm {MLE}$ no limite como $\ Alpha \ 0, \ \ beta \ to 0$ .

A distribuição preditiva posterior de dados adicional é um Gama-Poisson (ou seja binomial) de distribuição negativo.

A "lei dos pequenos números"

A palavra lei é por vezes utilizado como sinônimo de distribuição de probabilidade , e convergência em matéria significa convergência na distribuição. Assim, a distribuição de Poisson é chamado às vezes a lei dos pequenos números, porque é a distribuição de probabilidade do número de ocorrências de um evento que acontece raramente, mas tem muito muitas oportunidades para acontecer. A Lei das Pequenas Números é um livro de Ladislaus Bortkiewicz sobre a distribuição de Poisson, publicado em 1898 . Alguns historiadores da matemática têm argumentado que a distribuição de Poisson deve ter sido chamado a distribuição Bortkiewicz.

Calcular uma aproximação da probabilidade de Poisson

Quando k se torna grande (> 20) o uso de logs e aproximações fatoriais são necessários. Aqui está um exemplo escrito em Java.

 / ** Calcula uma aproximação da probabilidade de Poisson.  * @ Param média - lambda, o número médio de ocorrências *param observado - o número real de ocorrências observadasreturn * ln (probabilidade Poisson) - o log natural da probabilidade Poisson. */ public static double poissonProbabilityApproximation ( double mean, int observed ) { double k = observed ; double a = k * Math . log ( mean ) ; double b = - mean ; return a + b - factorialApproximation ( k ) ; } /**Srinivasa  Ramanujan ln (n!) Estimativa fatorial.  * Bom para maiores valores de n.  *return Ln (n!) */ public static double factorialApproximation ( double n ) { if ( n < 2 . ) return 0 ; double a = n * Math . log ( n ) - n ; double b = Math . log ( n * ( 1 . + 4 . * n * ( 1 . + 2 . * n ) ) ) / 6 . ; return a + b + Math . log ( Math . PI ) / 2 . ; }

Ferramentas de visualização on-line

SOCR GUI distribuição
Interativo Poisson Distribuição de TAMU

Retirado de " http://en.wikipedia.org/w/index.php?title=Poisson_distribution&oldid=197206369 "

Home Page - YouTube Channel