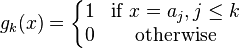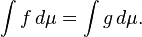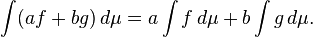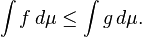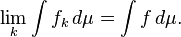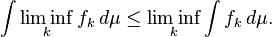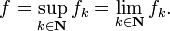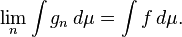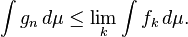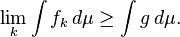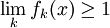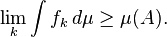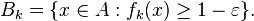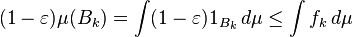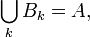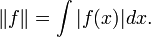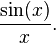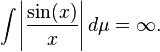Integração de Lebesgue
Informações de fundo
Crianças SOS produziu este website para as escolas, bem como este site de vídeo sobre a África . Clique aqui para saber mais sobre apadrinhamento de crianças.
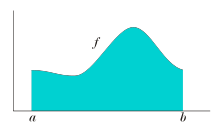
Em matemática , o integrante de um não-negativa função pode ser considerado no caso mais simples, como a área entre o . gráfico da função e que a integração eixo x Lebesgue é uma construção matemática que se estende a integral de uma classe maior de funções; que também se estende a domínios em que estas funções podem ser definidas. Há muito tempo se entendido que para funções não negativas com um gráfico bom o suficiente (como funções contínuas em fechado delimitada intervalos) a área sob a curva pode ser definido como o integral e calculado usando técnicas de aproximação da região pelos polígonos . No entanto, como a necessidade de considerar funções mais irregulares surgiu (por exemplo, como um resultado dos limitadores de processos de análise matemática e a matemática teoria das probabilidades ) tornou-se claro que seriam necessárias técnicas de aproximação mais cuidadosos para definir um integrante adequado. Além disso, poderíamos desejar para integrar em espaços mais gerais do que a linha real; a integral de Lebesgue fornece as abstrações direito necessários para fazer este trabalho importante.
A integral de Lebesgue desempenha um papel importante no ramo da matemática chamado análise real e em muitos outros campos das ciências matemáticas, e é nomeado após Henri Lebesgue (1875-1941), que introduziu a integral em (Lebesgue 1904). É também uma porção central do teoria axiomática de probabilidade.
O termo "integração de Lebesgue" pode se referir tanto a teoria geral da integração de uma função em relação a um general medir, como introduzido por Lebesgue, ou para o caso específico de integração de uma função definida em um sub-domínio do linha real com relação ao Medida de Lebesgue.
Introdução
O integral de uma função f entre limites a e b pode ser interpretado como a área sob o gráfico de f. Isso é fácil de entender para funções familiares, tais como polinômios , mas o que isso significa para funções mais exóticas? Em geral, o que é a classe de funções para as quais "área sob a curva" faz sentido? A resposta a esta questão tem grande importância teórica e prática.
Como parte de um movimento geral em direção rigor em matemática no século XIX, foram feitas tentativas para colocar o cálculo integral de uma base sólida. O Integral de Riemann, proposta por Bernhard Riemann (1826-1866), é uma tentativa largamente bem sucedida em proporcionar um tal fundação. Definição de Riemann começa com a construção de uma sequência de áreas facilmente calculados que convergem para o integrante de uma dada função. Esta definição é bem sucedida na medida em que dá a resposta esperada para muitos problemas já resolvidos, e dá resultados úteis para muitos outros problemas.
No entanto, a integração de Riemann não interage bem com a tomada de limites de sequências de funções, tornando tais processos limitam difíceis de analisar. Isto é de importância primordial, por exemplo, no estudo de Série de Fourier, Transformadas de Fourier e outros tópicos. A integral de Lebesgue é mais capaz de descrever como e quando é possível tomar limites sob o signo integral. A definição de Lebesgue considera uma classe diferente de áreas facilmente calculado que a definição de Riemann, que é a principal razão da integral de Lebesgue é melhor comportado. A definição de Lebesgue também faz com que seja possível calcular integrais para uma classe mais ampla de funções. Por exemplo, a Função de Dirichlet, que é 0, onde o seu argumento é irracional e 1 caso contrário, tem uma integral de Lebesgue, mas não tem uma integral de Riemann.
A abordagem de Lebesgue para a integração foi resumido em uma carta ao Paul Montel. Ele escreve:
Eu tenho que pagar uma certa quantia, o que eu coletei no meu bolso. Eu tomo as notas e moedas do bolso e dar-lhes ao credor na ordem que eu encontrá-los até que tenha alcançado a soma total. Este é o integral de Riemann. Mas eu posso proceder de forma diferente. Depois de eu ter tomado todo o dinheiro do meu bolso eu ordenar as notas e moedas de acordo com valores idênticos e então eu pagar os vários montes um após o outro para o credor. Este é o meu integral.- Fonte: (Siegmund-Schultze 2008)
A percepção é que um deve ser capaz de rearranjar os valores de uma função livremente enquanto preserva o valor do integral. Este processo de rearranjo pode converter uma função muito patológico em um que é "bom", do ponto de vista da construção e, portanto, permite que para tais funções patológicas a serem integrados.
Interpretação intuitiva
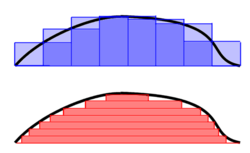
Para se ter uma intuição sobre as diferentes abordagens para a integração, vamos imaginar que se deseja encontrar o volume de um montanha (acima do nível do mar).
- A abordagem de Riemann-Darboux
- Divida a base da montanha em uma grade de 1 metro quadrados. Medir a altitude da montanha no centro de cada quadrado. O volume de uma única grelha quadrada é de cerca de 1 × 1 × (altitude), de modo que o volume total é a soma das alturas.
- A abordagem Lebesgue
- Desenhe um mapa de contorno da montanha, onde contornos adjacentes são de 1 metro de altitude à parte. O volume de terra contida em um único contorno é aproximadamente vezes a área do contorno que 1, de modo que o volume total é a soma das áreas destas vezes um metro.
Folland resume a diferença entre a Riemann e Lebesgue abordagens assim: "para calcular o integral de Riemann de F, um particiona o domínio [a, b] em subintervalos", enquanto que no Lebesgue, "é um efeito no particionamento da gama de f ".
Rumo a uma definição formal
Para definir a integral de Lebesgue formalmente requer a noção de um medida que, grosso modo, associa a cada conjunto A de números reais um número não negativo μ (a) Representar o "tamanho" de um. Esta noção de "tamanho" devem concordar com a duração habitual de uma união disjunta de intervalo ou intervalos. Suponha que f: R → R é uma função real não negativo. Usando o "particionar o intervalo de f" filosofia, a integral de f deve ser a soma de t das áreas entre uma tira horizontal fina entre y = t e y = t + dt. Esta área é apenas
Deixar
A integral de Lebesgue de f é, então, definido pela
onde a integral à direita é um ordinário imprópria integral de Riemann (note que f * é uma função estritamente decrescente positivo e, portanto, tem uma Riemann imprópria bem definida integral). Para uma classe adequada de funções (a funções mensuráveis) Isto define a integral de Lebesgue.
Um geral (não necessariamente positivo) função f é Lebesgue integrável se a área entre o gráfico de f e o eixo x é finito:
Nesse caso, o integral é, como no caso de Riemannian, a diferença entre a área acima do eixo x e área abaixo do eixo x:
onde
Construção

A discussão que segue paralela à abordagem expositiva mais comum para a integral de Lebesgue. Nesta abordagem, a teoria de integração tem duas partes distintas:
- A teoria dos conjuntos mensuráveis e medidas sobre esses conjuntos.
- A teoria de funções mensuráveis e integrais sobre estas funções.
A função cujo integral é para ser encontrada é, em seguida, determinado por uma aproximação chamada funções simples, cuja integrais podem ser escritos em termos da medida. O integral da função original é, então, o limite do integral das funções simples.
Teoria da medida
Teoria da medida foi inicialmente criado para fornecer uma abstração útil da noção do tempo de subconjuntos da reta real e, mais geralmente, a área eo volume de subconjuntos de espaços euclidianos. Em particular, é fornecida uma resposta sistemática à questão de qual dos subconjuntos R têm um comprimento. Como foi mostrado por desenvolvimentos posteriores na teoria dos conjuntos (ver conjunto não mensurável), é realmente impossível atribuir um comprimento de todos os subconjuntos de R de uma forma que preserva algumas aditividade e tradução de invariância propriedades naturais. Isto sugere que escolher uma classe apropriada de subconjuntos mensuráveis é um pré-requisito essencial.
A integral de Riemann usa a noção de comprimento explicitamente. Na verdade, o elemento de cálculo do integral de Riemann é o rectângulo [a, b] x [c, d], cuja área é calculada como sendo (b - a), (d - c). A quantidade b - a é o comprimento da base do rectângulo e d - c representa a altura do rectângulo. Riemann só poderia utilizar rectângulos planares para aproximar a área sob a curva porque não havia nenhuma teoria adequada para medir conjuntos mais gerais.
No desenvolvimento da teoria na maioria dos livros de texto modernos (depois de 1950), a abordagem para medir e integração é evidente. Isto significa que uma medida é qualquer função μ definida sobre uma certa classe X de subconjuntos de um conjunto E, o que satisfaz uma determinada lista de propriedades. Estas propriedades podem ser exibidas para segurar, em muitos casos diferentes.
Integração
Começamos com um espaço de medida (E, X, μ), onde E é um conjunto , X é um σ-álgebra de subconjuntos de E e μ é uma (não- negativo) medir em E, definido nos sets de X.
Por exemplo, E pode ser euclidiana n -espaço R n ou alguns Lebesgue subconjunto mensurável de que, X será o σ-álgebra de todos os subconjuntos mensuráveis de Lebesgue de E e μ será o Medida de Lebesgue. Na teoria matemática das probabilidades, nós limitar nosso estudo a uma probabilidade μ medida, que satisfaz μ (E) = 1.
Na teoria de Lebesgue, integrais são definidos para uma classe de funções chamada funções mensuráveis. A função F é mensurável se o pré-imagem de cada intervalo da forma (t, ∞) é em X:
Pode ser mostrado que isso é equivalente a exigir que a pré-imagem de qualquer Borel subconjunto de R estar em X. Vamos fazer essa suposição daqui em diante. O conjunto de funções mensuráveis é fechado sob operações algébricas, mas mais importante que a classe é fechada sob vários tipos de pointwise limites seqüenciais:
são mensuráveis se a sequência original k (f k), onde k ∈ N, consiste de funções mensuráveis.
Construímos uma integral
para funções reais mensuráveis f definido em E em etapas:
Indicador Funções: Para atribuir um valor para a integral da Função do indicador de 1 S de um conjunto mensurável S consistente com a medida dada μ, a única opção razoável é definir:
Note-se que o resultado pode ser igual a + ∞, a menos que μ é uma medida finita.
Funções simples: um finito combinação linear de funções indicadoras
em que os coeficientes a k são números reais e os conjuntos S k são mensuráveis, é chamado um mensurável função simples. Nós estendemos a integral por linearidade para funções simples mensuráveis não negativas. Quando os coeficientes de um k são não-negativo, montamos
A convenção 0 × ∞ = 0 deve ser usado, e o resultado pode ser infinita. Mesmo se uma função simples pode ser escrita em muitas formas como uma combinação linear de funções indicadoras, a integral será sempre o mesmo; isso pode ser mostrado usando a propriedade de aditividade de medidas.
É necessário algum cuidado ao definir a integral de uma função simples de valor real, para evitar a expressão indefinida ∞ - ∞: supõe-se que a representação
é tal que μ (S k) <∞ sempre que um k ≠ 0. Em seguida, a fórmula acima para o integral de f faz sentido, e o resultado não depende de a representação particular de f satisfazendo os pressupostos.
Se B é um subconjunto mensurável de E e s é uma função simples mensurável se define
Funções não negativas: Seja f uma função mensurável não negativa sobre E que nós permitimos que para atingir o valor + ∞, em outras palavras, f toma valores não-negativos no alargado linha número real. Definimos
Precisamos mostrar isto coincide integrais com o anterior, definida no conjunto de funções simples. Quando E é um segmento [a, b], há também a questão de saber se este corresponde de forma alguma a uma noção de Riemann de integração. É possível provar que a resposta a ambas as perguntas é sim.
Nós definimos a integral de f para qualquer função real estendida não negativo mensurável sobre E. Para algumas funções, este ∫ E f dμ integrante será infinito.
Funções assinados: Para lidar com funções assinados, precisamos de mais algumas definições. Se f é uma função mensurável do conjunto E para os reais (incluindo ± ∞), então podemos escrever
onde
Note-se que tanto f + e f - são funções mensuráveis não negativas. Observe também que
Nós dizer que o integral da função de Lebesgue mensurável f existe, ou se é definido, pelo menos, um dos 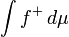 e
e 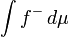 é finito:
é finito:
Neste caso, nós definimos
Se
dizemos que f é Lebesgue integrável.
Acontece que esta definição dá as propriedades desejáveis da integral.
Complexas funções podem ser valorizados da mesma forma integrada, considerando-se a parte real ea parte imaginária separadamente.
Exemplo
Considere o função de indicador dos números racionais, 1 Q. Esta função é nenhuma parte contínua.
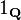 não é Riemann integrável em [0,1]: Não importa como o conjunto [0,1] é particionado em subintervalos, cada partição irá conter pelo menos um racional e pelo menos um número irracional, porque racionais e irracionais são ambos denso em os reais. Assim, o superior Somas de Darboux serão todos um, e as somas inferiores Darboux serão todos zero.
não é Riemann integrável em [0,1]: Não importa como o conjunto [0,1] é particionado em subintervalos, cada partição irá conter pelo menos um racional e pelo menos um número irracional, porque racionais e irracionais são ambos denso em os reais. Assim, o superior Somas de Darboux serão todos um, e as somas inferiores Darboux serão todos zero.
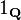 é Lebesgue-integrável em [0,1] usando o Medida de Lebesgue: Na verdade, é a função de indicador das rationals assim, por definição,
é Lebesgue-integrável em [0,1] usando o Medida de Lebesgue: Na verdade, é a função de indicador das rationals assim, por definição,
- Q é porque contável.
Domínio de integração
Um problema técnico na integração de Lebesgue é que o domínio de integração é definido como um conjunto (um subconjunto de um espaço de medida), sem noção de orientação. No cálculo elementar, define uma integração em relação a um Orientação:
Generalizando este para dimensões maiores rendimentos integração de formas diferenciais. Em contraste, a integração de Lebesgue fornece uma generalização alternativa, integrando sobre subconjuntos com respeito a uma medida; isso pode ser notado como
para indicar integração sobre um subconjunto A. Para obter detalhes sobre a relação entre essas generalizações, consulte Forma diferencial: Relação com medidas.
Limitações da integral de Riemann
Aqui nós discutimos as limitações da integral de Riemann e maior alcance oferecido pela integral de Lebesgue. Nós presumimos uma compreensão de trabalho do Integral de Riemann.
Com o advento de Série de Fourier, muitos problemas analíticos envolvendo integrais surgiu cuja solução satisfatória necessária trocando processos limite e sinais de integral. No entanto, as condições em que as integrais
são iguais se mostrou bastante evasivo no âmbito de Riemann. Existem algumas outras dificuldades técnicas com o integral de Riemann. Estes estão relacionados com a dificuldade de tirar o limite discutido acima.
Falha de convergência monótona. Como mostrado acima, o Função do indicador de 1 Q sobre os racionais não é Riemann integrável. Em particular, o Teorema da convergência monótona falhar. Para ver porque, vamos {a k} uma enumeração de todos os números racionais em [0,1] (são contável de modo que este pode ser feito.) Então deixe-
A função g k é zero em todos os lugares, exceto em um conjunto finito de pontos, daí o seu integral de Riemann é zero. A sequência de g k também é claramente não-negativo e aumenta monotonicamente com 1 Q, que não é Riemann integrável.
Inadequação para intervalos não limitados. A integral de Riemann só pode integrar funções em um intervalo limitado. Pode, contudo, ser estendido a intervalos não limitados tomando limites, desde que este não produz uma resposta tal como ∞-∞.
A integração em outros do que o espaço euclidiano estruturas. A integral de Riemann está indissoluvelmente ligada à estrutura fim da linha.
Teoremas básicos da integral de Lebesgue
A integral de Lebesgue não distingue entre as funções que diferem apenas em um conjunto de μ-medida zero. Para fazer esta precisos, as funções f e g são referidos como sendo igual quase todos os lugares (ae) se
- Se f, g são funções mensuráveis não negativas (possivelmente assumindo o valor + ∞) tal que f = g em quase toda parte, em seguida,
A saber, a integral respeita a relação de equivalência de quase todos os lugares-igualdade.
- Se f, g são funções de tal modo que f = g em quase toda parte, então f é Lebesgue integrável se e somente se g é Lebesgue integrável, e as integrais de f e g são o mesmo se existirem.
O integral de Lebesgue tem as seguintes propriedades:
Linearidade: Se f e g são funções integráveis de Lebesgue e a e b são números reais, então af + bg é Lebesgue integrável e
Monotonicidade: Se f ≤ g, então
Teorema da convergência monótona: Suponha que {f k} k ∈ N é uma seqüência de funções não negativas mensuráveis tais que
Em seguida, o limite pointwise f de f k é Lebesgue integrável e
Nota: O valor de qualquer um dos integrais é permitido ser infinita.
Lema de Fatou: se {f k} k ∈ N é uma sequência de funções mensuráveis não negativas, em seguida,
Mais uma vez, o valor de qualquer dos integrais pode ser infinita.
Teorema de convergência dominante: Suponha {f k} k ∈ N é uma sequência de funções mensuráveis complexos com limite f pontual, e não é uma função integrável Lebesgue g (isto é, g pertence à espaço L 1) tal que | f k | ≤ g para todo k.
Então, f é Lebesgue integrável e
Técnicas de prova
Para ilustrar algumas das técnicas de prova utilizados na teoria da integração de Lebesgue, esboçamos uma prova do acima mencionado Lebesgue da convergência monótona teorema. Seja {f k} k ∈ N ser uma sequência não-decrescente de funções mensuráveis não negativas e colocar
Pela propriedade monotonia da integral, é imediato que:
e existe o limite à direita, porque a seqüência é monótona. Nós agora provar a desigualdade na outra direção. Daqui resulta a partir da definição de integral que existe uma sequência não decrescente (g n) das funções simples não-negativos de tal forma que n ≤ g f e
Por conseguinte, basta que se prove que, para cada n ∈ N,
Vamos mostrar que se g é uma função simples e
quase todos os lugares, em seguida,
Ao romper-se a função g nas suas partes valor constante, o que reduz ao caso em que g é a função de indicador de um conjunto. O resultado temos de provar é, então,
Suponha que A é um conjunto mensurável e {f k} k ∈ N é uma sequência não-decrescente de funções mensuráveis não negativas sobre E tal que
para quase todo x ∈ A. Em seguida
Para provar este resultado, corrigir ε> 0 e definir a seqüência de conjuntos mensuráveis
Por monotonicidade do integrante, segue-se que para qualquer k ∈ N,
Porque quase todos os x será em B k para k grande o suficiente, temos
-se a um conjunto de medida 0. Assim, por aditividade contável de μ, e porque B k aumenta com k,
Como isso é verdade para qualquer ε positivo o resultado segue.
Formulações alternativas
É possível desenvolver o integral no que diz respeito à medida de Lebesgue sem depender da maquinaria completa da teoria da medida. Uma tal abordagem é fornecido pela Daniell integral.
Há também uma abordagem alternativa para o desenvolvimento da teoria de integração através de métodos análise funcional. Existe a integral de Riemann para qualquer função contínua de f suporte compacto definido em R n (ou um subconjunto aberto fixo). Integrais de funções mais gerais podem ser construídos a partir destes integrais.
Vamos C c ser o espaço de todas as funções contínuas compactamente suportadas de valor real de R. Definir uma norma sobre C c por
Depois, C c é um espaço vectorial normalizado (e em particular, é um espaço métrico.) Em todos os espaços têm métricas Completação de Hausdorff, então vamos L 1 seja a sua conclusão. Este espaço é isomorfo ao espaço de Lebesgue funções integráveis módulo subespaço de funções com integral zero. Além disso, o integral de Riemann ∫ é um uniformemente contínua funcional com respeito à norma em C c, que é densa em L 1. Assim ∫ tem uma extensão única para todos L 1. Esta integral é precisamente a integral de Lebesgue.
De modo mais geral, quando o espaço medida em que as funções são definidas é também um localmente compacto espaço topológico (como é o caso com os números reais R), mede compatível com a topologia num sentido adequado ( Medidas de radão, dos quais a medida de Lebesgue é um exemplo) uma integral com respeito a eles podem ser definidas da mesma forma, a partir dos integrais de funções contínuas com suporte compacto. Mais precisamente, as funções de suporte compacta formar um espaço vector que transporta um naturais topologia, e um (Radon) medida é definida como uma contínua linear funcional neste espaço. O valor de uma medida em função de uma forma compacta, em seguida, também é suportada por definição, o integral da função. Uma então começa a expandir a medida (a integral) para funções mais gerais pela continuidade, e define a medida de um conjunto como o integrante da sua função de indicador. Esta é a abordagem adoptada pela Bourbaki (2004) e um certo número de outros autores. Para mais detalhes veja Medidas de radônio.
Limitações da integral de Lebesgue
O principal objetivo do integral de Lebesgue é fornecer uma notação integrante onde os limites de integrais mantenha sob pressupostos leves. Não há garantia de que cada função é Lebesgue integrável. Pode acontecer que impróprios (Riemann) integrais existem para funções que não são de Lebesgue integrável. Um exemplo seria
Esta função não é Lebesgue integrável como
Por outro lado, existe como uma inadequada Riemann integral e o integral pode ser calculado para ser finito. Um conceito equivalente a integral imprópria Lebesgue não existe porque tal perspectiva não é necessário do ponto de vista dos teoremas de convergência.
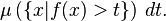



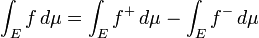

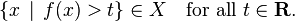
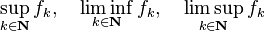

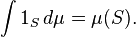
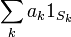
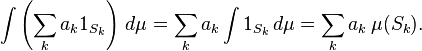




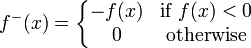
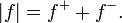



![\ Int _ {[0,1]} 1 _ {\ mathbf Q} \, d \ mu = \ mu (\ mathbf {Q} \ cap [0,1]) = 0,](../../images/2452/245211.png)

![\ Int_A f \, d \ mu = \ int _ {[a, b]} f \, d \ mu](../../images/2452/245213.png)
![\ Sum_k \ int F_k (x) dx, \ quad \ int \ left [\ sum_k F_k (x) \ right] dx](../../images/2452/245214.png)